 (Man beachte, dass da
3 zu sehen sind.)
(Man beachte, dass da
3 zu sehen sind.)möglichst 1fach
(schwierig wird's noch früh genug)
| "Nenne mir eine einfache Zahl." "Sieben." "Geht's nicht noch einfacher?" "Zwei." "Noch einfacher!" "Eins." "Danke." |
Das weiß ich natürlich auch, dass die Schreibweise "1fach" "einsfach" bedeuten würde - und somit schlichtweg falsch ist. Aber mir geht's in einem kleinen Wortspiel ja um die Einfachheit der Eins.
Nebenbei:
![]()
 (Man beachte, dass da
3 zu sehen sind.)
(Man beachte, dass da
3 zu sehen sind.)
Jede Wette, dass das Folgende in keinem einzigen der gängigen Mathe-Schulbücher vorkommt. Und genau das ist eben symptomatisch: dass in Schulbüchern keine zentralen Denkweisen vorkommen, vor lauter Bäumen also nicht mehr der Wald gezeigt wird.
Warum einfach, wenn's auch kompliziert geht
(womit ich mich keineswegs billig über Grundsatzüberlegungen lustig machen will)?:
Ein Grundproblem der Mathematik besteht darin, dass man oftmals unvermeidbar die Wahl zwischen Pest und Cholera hat, nämlich
Und da stellt sich dann die Frage, was eigentlich pädagogisch günstiger ist:
Ein Beispiel:
Aus prinzipiellen Gründen gibt es aber keinen Kreis, der
Hier geht es nicht darum, dass die Eins (natürlich!) die einfachste überhaupt denkbare Zahl ist, sondern darum, wie praktisch sie oftmals in anderen Zusammenhängen ist und wie sie in der Mathematik systematisch zum Erkenntnisgewinn eingesetzt wird
Dafür einige Beispiele aus unterschiedlichsten Bereichen der Schulmathematik
(und überhaupt erst die Unterschiedlichkeit der Bereiche zeigt das Grundprinzip):
(z.B. ![]() ,
,![]() oder auch
oder auch ![]() )
)
gerechnet, aber üblicherweise wird nur eine einzige dieser
(oder genauer: der irrationalen)
Wurzeln genauer betrachtet, nämlich ![]() .
.
Schauen wir uns mal genau an, was da passiert: meist ausschließlich anhand der ![]() wird gezeigt
wird gezeigt
dass diese Zahl irrational, d.h.
Und daraus zieht man prompt die ebenso radikale wie resignierte Konsequenz, die Dezimalschreibweise von ![]() überhaupt nicht mehr zu benutzen
überhaupt nicht mehr zu benutzen
(![]() schon gar nicht in den Taschenrechner einzugeben)
schon gar nicht in den Taschenrechner einzugeben)
und somit auch nicht mehr mit ![]() zu rechnen - mit der kleinen, aber gewichtigen Ausnahme (
zu rechnen - mit der kleinen, aber gewichtigen Ausnahme (![]() )2 = 2.
)2 = 2.
Der Beweis, dass ![]() irrational ist, dient dabei dazu, an dem einzigen Beispiel
irrational ist, dient dabei dazu, an dem einzigen Beispiel ![]()
Da dieses Beweisverfahren aber arg umständlich ist und schon allein bei ![]() viel Arbeit bereitet hat, spart man es sich, dieses Verfahren auch noch für andere Wurzeln durchzuführen. Es reicht, anhand von
viel Arbeit bereitet hat, spart man es sich, dieses Verfahren auch noch für andere Wurzeln durchzuführen. Es reicht, anhand von ![]() das (immer gleiche) Beweisprinzip kennengelernt zu haben, und eine erneute Anwendung auf andere Wurzeln wäre nur noch langweilig, letztlich aber auch aussichtslos, da es unendlich viele irrationale Wurzeln gibt.
das (immer gleiche) Beweisprinzip kennengelernt zu haben, und eine erneute Anwendung auf andere Wurzeln wäre nur noch langweilig, letztlich aber auch aussichtslos, da es unendlich viele irrationale Wurzeln gibt.
Wie schon gesagt, ist jegliches direkte Rechnen mit irrationalen Wurzeln aussichtslos, und deshalb führt man das Rechnen mit Wurzeln mittels der Wurzelgesetze auf das simple Rechnen mit rationalen Zahlen zurück:
![]()
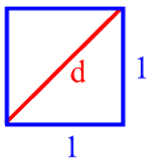
Wie aber kommt man auf die Irrationalität von ![]() ?: merkwürdiger- und doch gleichzeitig auch bezeichnenderweise, indem man mit dem 1fachsten überhaupt nur denkbaren geometrischen Gegenstand, nämlich
?: merkwürdiger- und doch gleichzeitig auch bezeichnenderweise, indem man mit dem 1fachsten überhaupt nur denkbaren geometrischen Gegenstand, nämlich
anfängt und dann feststellt, dass bereits die 1fachste Linie in diesem Quadrat, nämlich die Diagonale d, die irrationale Länge ![]() hat:
hat:
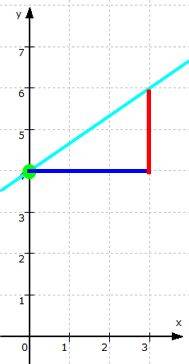
Da kann man sich streiten, welches Verfahren
man geht vom Punkt P (0 | 4 )
 .
.
Ein Beispiel: in einer 9. Klasse
stellte sich ein Schüler die Aufgabe, den Böschungswinkel ![]() der Cheopspyramide zu berechnen:
der Cheopspyramide zu berechnen:
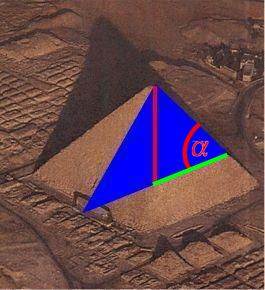
Nun wusste ich ja, dass den Neuntklässlern das nötige Werkzeug für solch eine Winkelberechnung, nämlich die Trigonometrie, noch nicht zur Verfügung stand, und da kann man sich streiten, was besser ist:
Ich habe leider den ersten Weg gewählt, also versucht, dem Schüler die Aussichtslosigkeit seines Handelns klarzumachen, aber glücklicherweise hat er sich dennoch nicht von seinem Weg abbringen lassen - und folgendermaßen mit dem Dreisatz argumentiert:
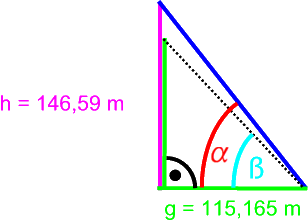
| : | = ![]() : ß
: ß
Wenn man nun noch hinzunimmt, dass ß in dem gleichschenkligen, aus den beiden |-Seiten gebildeten Dreieck offensichtlich 450 ist, so ergibt sich
![]() .
.
Und wenn man das nach ![]() auflöst, ergibt sich
auflöst, ergibt sich ![]() ≈ 570.
≈ 570.
Nun bin ich ja keineswegs immer sofort in der Lage zu überblicken, ob intelligente oder auch verschrobene alternative Lösungsansätze von SchülerInneN richtig oder falsch sind
(und sie können ja auch teilweise richtig sein, also gleichzeitig gute und falsche Ideen enthalten).
Genau dieses Unvermögen, auf Anhieb zu erkennen, ob eine Schüler-Lösung richtig oder falsch ist, sollte man als Lehrer aber offen zugeben, wenn nicht sogar regelrecht ausstellen, also auch die Möglichkeit "einräumen", dass einE SchülerIn eventuell schlauer als man selbst ist.
(... was doch prima fürs [auch kollektive] Selbstbewusstsein der SchülerInnen wäre).
Der gute Lehrer ist dann wohl jener, der ein Problem auf den Prüfstand stellen kann.
"Prüfstand" darf dabei aber nicht bedeuten, dass der Schülervorschlag unter Generalverdacht gerät
("der Vorschlag ist - weil von einem Schüler - sowieso falsch"),
sondern es müsste eine offene Forschungssituation entstehen, so dass erst ganz am Ende klar würde, ob der Schülervorschlag falsch (oder ungenau) oder aber korrekt war.
Und am besten errichtet nicht der Lehrer allein den Prüfstand
(bei einem falschen Schülervorschlag oftmals ja doch sehr wohl wissend, worin der Denkfehler des Schülers bestand; also den Prüfstand gleich so organisierend, dass er allzu strigent auf eine Widerlegung des Schülervorschlags hinausläuft),
sondern wird mit den SchülerInneN gemeinsam überlegt, wie man den Schülervorschlag überprüfen könnte.
Viel gefährlicher, als dass der Lehrer "auch" nicht weiß, ob ein Schülervorschlag richtig oder falsch ist, ist es vielleicht sogar, dass er das sofort erkennt:
Im vorliegenden Pyramiden-Basiswinkel-Fall wusste ich allerdings auf Anhieb, dass das Ergebnis falsch war, und zwar
(auch so wird man schnell betriebsblind für Alternativwege),
Eine dann erst erfolgte Schnellrecherche in Wikipedia hat für den Böschungswinkel ![]() = 520 ergeben (vgl.
= 520 ergeben (vgl. ![]() ).
).
Wenn man nicht einfach sagt, dass 570 und 520 sehr nach beeinander liegen, und
"so genau will's doch auch gar keiner wissen";
und wenn man zudem nicht einfach ex cathedra
"Gott und all seine Stellvertreter auf Erden [der Papst, der Lehrer und »das« Internet] haben sowieso immer recht"
(§ 1: Der Lehrer hat immer Recht.
§ 2: Sollte der Lehrer einmal nicht Recht haben,
tritt automatisch § 1 in Kraft.)
voraussetzt, so haben wir hier - hochtragend gesagt - einen "kognitiven Konflikt":
Um nicht mit komplizierten und eventuell gerundeten Werten zu rechnen, ver1fachen wir folgendermaßen
(indem wir das grundlegende Konstruktionsprinzip der Cheopspyramide beibehalten, aber all ihre schiefen Werte beseitigen):
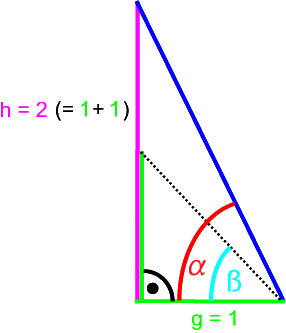
Nach obiger Logik gilt
| : | = ![]() : ß .
: ß .
Einsetzen ergibt
2 : 1 = ![]() : 450 ,
: 450 ,
und daraus folgt ![]() = 900.
= 900.
Das widerspricht aber völlig der Zeichnung, in der ![]() ≈ 630.
≈ 630.
Tatsächlich scheint also an unserem Denkweg etwas nicht zu stimmen.
Der einzig "wahre" Denkweg wäre hier der Tangens, den die SchülerInnen aber noch nicht kennen
(und wohl auch kaum "so nebenher" entdecken oder auch nur vermittelt bekommen können).
Ich hatte oben mehrfach (wenn auch variiert) von "nicht völlig falsch, so doch ungenau" gesprochen. Denn man sollte doch unbedingt anerkennen, dass der Schüler mit | : |
(also Gegen- zu Ankathete)
annähernd selbstständig den Tangens entdeckt hat.
D.h. man sollte nicht seinen Fehler tadeln, sondern sein enorm selbstständiges und vorausschauendes Procedere in höchsten Tönen loben.