Ästhetik der Mathematik
vgl. auch ![]() Projekt Mathematik und Kunst
Projekt Mathematik und Kunst![]()
litauische Übersetzung: 
![]() H. Stauff. Matematikos estetika
H. Stauff. Matematikos estetika
"Die Werke des Mathematikers müssen schön sein wie die des Malers oder Dichters; die Ideen müssen harmonieren wie die Farben oder Worte. Schönheit ist die erste Prüfung: es gibt keinen Platz in der Welt für häßliche Mathematik."
(G. H. Hardy)
"Es ist schwer, einen Begriff von der Ausdehnung der modern Mathematik zu vermitteln. Schon das Wort »Ausdehnung« ist nicht zutreffend: Ich meine eine von schönen Einzelheiten erfüllte Weite - nicht eine Weite im Sinn einer eintönigen Ebene, sondern eine weite schöne Landschaft, die man zuerst aus der Ferne bewundert, die aber wert ist, durchwandert und in allen Einzelheiten ihrer Hügel und Täler, ihrer Bäche, Felsen, Bäume und Blumen studiert zu werden. Doch wie für so manches gilt auch für ein mathematische Theorie: Schönheit läßt sich wahrnehmen, aber nicht erklären."
(Arthur Cayley)
"Die Mathematik, recht betrachtet, besitzt nicht nur Wahrheit, sondern auch höchste Schönheit - eine kalte und strenge Schönheit gleich einer Skulptur, ohne Anziehungskraft für irgendeine unserer schwächeren Seiten, ohne die prächtigen Anreize der Malerei oder der Musik, aber von erhabener Reinheit und einer strengen Vollendung, wie sie nur höchste Kunst aufweisen kann."
(Bertrand Russell)
"Reine Mathematik ist in ihrer Art die Poesie logischer
Ideen."
(Albert Einstein)

Arch of the West, Saint Louis
Aber warum in die Ferne schweifen, wo das Gute liegt so nah?:

Neue Brücke der Wolbecker Straße in Münster über den Kanal, März 2021
Oder umgekehrt: warum in die Nähe schweifen, wo das Gute liegt so fern:
.jpg)
Im Jahr 2021 mit 112 m höchste Bogenbrücke der Welt in Zangmu (China)
Daß Mathematik ästhetisch, ja, daß diese Ästhetik in den Augen eines "echten" Mathematikers ihr höchster Zweck sein könne, wird vielleicht vielen Nicht-Mathematikern oder gar Mathematik-Hassern unverständlich bis geradezu "pervers" erscheinen.
Und das scheint mir zwei Gründe zu haben:
den, daß man gar nicht einsieht, was ausgerechnet an solch einer knochentrockenen und theoretischen Wissenschaft ästhetisch, also schön sein solle (auf diesen vordergründig berechtigten, ja teilweise durchaus richtigen Einwand wird zurückzukommen sein);
und viel allgemeiner aber vielleicht den, daß man von allem und jedem im Leben (und insbesondere von der Mathematik?) eine äußere Zweckdienlichkeit und Anwendbarkeit erwartet, Schönheit also nicht als Selbstzweck akzeptieren kann.
Üblicherweise wird bei Mathematik oft rhetorisch gefragt: "was habe ich davon, wo kann ich das jemals wieder gebrauchen, wo ist das anwendbar?" Die vordergründige Antwort auf diese rhetorische Frage ist "nichts" bzw. "nirgends". Vordergründig, weil jeder ganz genau weiß, daß die Mathematik sehr wohl anwendbar ist, daß unsere gesamte technische Kultur auf ihr beruht. Aber die Frage "was habe ich davon, wo kann ich das jemals wieder gebrauchen?" stellt vielleicht gar nicht eine allgemeine Anwendbarkeit in Frage, sondern nur, daß das "Ich" jemals Mathematik gebrauchen kann. Wie ein bielefelder Professor mal "rausgefunden" hat: der "Durchschnittsmensch" braucht im "normalen" Leben höchstens die Mathematik bis zur 7. Klasse, also etwa die Grundrechenarten und Ansätze der Gleichungslehre (Dreisatz) und ein bißchen Prozentrechnung.
Die rhetorische Frage nach der Anwendbarkeit der Mathematik für einen selbst impliziert wohl eher die Antwort: "sicherlich kann man das gebrauchen - aber ich nicht; ich bin zu blöd dazu (oder will es gar nicht)". Die rhetorische Frage nach der Anwendbarkeit der Mathematik impliziert, so scheint mir, also oftmals schon die Resignation vor einer Expertokratie, von der man sich von Anfang an ausgeschlossen fühlt - bzw. sich selbst von Anfang an ausschließt (vgl. den Familienmythos und somit die Selbstentschuldigung: "schon meine Großmutter hat keine Mathematik gekonnt").
In der Frage, wozu Mathematik gut sei und ob man sie verstehen könne; aber auch im Umstand, daß Mathematik in den Schulen zu den unbeliebtesten Fächern gehört sowie jenen, die die meisten Sitzenbleiber hervorbringen, scheint sich mir ein viel grundsätzlicheres Problem auszudrücken: ein durchaus berechtigtes Unwohlsein mit
unserer theoretischen Expertenkultur,
einer gewissen dominanten abstrakten Weltdeutung,
einer (scheinbar) eiskalten, arg simpel zweiwertigen Logik: ganz wahr oder ganz falsch - und nichts dazwischen;
einer (scheinbar) abgenagten Formelästhetik.
Es sei doch kurz auf die oftmalige "Schizophrenie" hingewiesen: auf der einen Seite verlangen mathematische Laien oft nach Anwendbarkeit, auf der anderen Seite stört sie gerade diese komplette Durchmathematisierung der Wirklichkeit. Ja, oftmals haben ausgerechnet die Mathematik-Hasser den allergrößten Respekt vor Mathematik. Aber vielleicht ist das nur Ausläufer einer viel allgemeineren "Schizophrenie" heutzutage: daß ausgerechnet die größten Nutznießer des Systems gleichzeitig ihre einseitigsten Kritiker sind, daß also z.B. auch Technizismus einerseits und Technikfeindlichkeit andererseits, modernster (Manchester-)Kapitalismus einerseits und Nostalgie andererseits, Rationalismus einerseits und Antirationalismus (z.B. Esoterik) andererseits sehr wohl in ein und denselben Kopf passen.
Nicht daß ich sowas für eine Krankheit erst unserer Zeit halte. Vielmehr scheint mir, daß es erstens schon seit der Jahrhundertwende, wenn nicht gar seit Beginn der Neuzeit, ja, der Erfindung der Theorie im alten Griechenland diese Kluft, dieses "Unbehagen in der Kultur" (Freud) gibt. Und zweitens ist es wohl "natürliche" Folge einer komplexen Wirklichkeit, die nunmal nicht nur auf einer (widerspruchsfreien) Ebene erklärbar ist. Es sei nur daran erinnert, daß wir alle die Heliozentrik "wissen", im Alltag aber die Geozentrik "glauben": "die Sonne geht auf", und die Mondphasen werden oftmals als Mondfinsternis (bei feststehender Erde) erklärt.
Die große Sinn-Integration fehlt. Sie ist auch nicht (mehr) so einfach zu bekommen. Und doch scheint mir, daß auf das Leiden der Menschen an der dargestellten "Schizophrenie" reagiert werden muß.
Auch in der Mathematik; oder genauer: in der Schul-Mathematik, also dann, wenn Menschen (Schüler) "system"atisch zu ihr gezwungen werden (umgekehrt: gerade der Zwang legt es nahe, ihn erst gar nicht zu begründen; was doch wohl hieße: immer ideologische Verbrämungen und Pseudo-Begründungen zu liefern.)
Die Schulmathematik muß sich darüber klar werden bzw. bleiben, weshalb sie überhaupt Schulfach geworden ist (denn es ist doch wohl völlig naiv zu meinen, der heutige Fächerkanon sei selbstverständlich sowie voraussetzungs- und interesselos): Mathematik dient dazu, eine bestimmte Art des logischen und formalen Denkens, also auch eine bestimmte Form der Wirklichkeitswahrnehmung zu vermitteln (bzw. im allerbesten Sinne dazu, zum souverän-kritischen Umgang damit zu befähigen: die Möglichkeiten, aber auch Grenzen dieser Wirklichkeitswahrnehmung zu zeigen). Mathematik - wie jedes Schulfach - ist also interessegelenkt, und solches Interesse ist nie selbstverständlich-unproblematisch.
(Ich möchte unbedingt ergänzen, daß Mathematik - wie jedes Fach - ihren Wert und ihre Relativierung erst durch andere Schulfächer findet, wenn man mal davon absieht, daß fast alle Schulfächer rein kognitiv arbeiten; was ja wichtig ist und doch einseitig bleibt. Und ein Mittel gegen die kognitive Überfrachtung ist eben die u.g. Ästhetik.)
In die Schulmathematik gehört also dringend eine Reflexion der o.g. "Schizophrenie" - sowie eine Reflexion darüber, wo die Mathematik ursächlich an ihr teilhat, sie gar befördert.
D.h. auch: es ist ja noch lange nicht ausgemacht, daß die Schulmathematik derart laufen muß, wie sie derzeit an Schulen "verbraten" wird
(meistens, weil die Lehrer sie auch schon nicht anders gelernt haben; welcher Mathematiklehrer hat denn beispielsweise Kenntnisse über die Philosophie und Geschichte der Mathematik?).
Nun sind die genannte Unbeliebtheit des Faches Mathematik und der Umstand, daß dieses Fach so viele Sitzenbleiber produziert, ja keineswegs nur "Schuld" der Mathematik oder gar der individuellen Mathematik-Lehrer. Nein, da rächt sich einerseits o.g. allgemeine kulturelle Schizophrenie (fast hätte ich gesagt: die Rache der Banausen, der kulturell Überforderten), andererseits ist gegen die platten Vorurteile gegenüber Mathematik oftmals schon gar nicht mehr anzukommen.
Wie an anderen Fächern stört an Mathematik wohl vor allem, daß es Schulfach ist, d.h. am Fach rächt sich das System: im Grunde bleibt es skandalös, Liebesgedichte oder den Satz des Pythagoras als Prüfungsmittel zu mißbrauchen! Kein Wunder, daß in solchen Gegenständen dann von SchülerInnen nur noch ein Prüfungsgegenstand und Knüppel gesehen wird.
Die Schul-Mathematik sollte sich auch darüber klar werden, daß sie oftmals (durch einseitige Lehrer und Lehrpläne) auch einseitige Schüler fördert: häufig eben nicht - so möchte ich behaupten - die "wirklichen", d.h. offenen, ästhetischen Mathematiker, sondern die Engstirnigen, Eiskalten, fast hätte ich gesagt: Lebensuntüchtigen, die in der Strenge der Mathematik den letzten Strohhalm finden, an dem sie ihr dürftiges, unkreatives Leben aufhängen können - und ab dann alles und jedes nach billigster zweiwertiger Logik und Beweisbarkeit bewerten. Man achte mal darauf, mit welch abstruser Spitzfindigkeit und Bildlosigkeit gerade "gute" Mathematiker unter Schülern dann etwa an ein Liebesgedicht gehen.
Ich finde es nämlich schon erstaunlich, daß oftmals gerade die (scheinbar) guten Mathematiker am allerwenigsten mit einer wissenschaftstheoretischen und historischen oder gar ästhetischen Grundlagendiskussion der Mathematik anfangen können, ja, geradezu verbiestert darauf reagieren. Man spürt ihnen die totale Verunsicherung an: daß ihnen durch eine Problematisierung der Grundlagen und auch der gesellschaftlichen Position von Mathematik ihr letztes Fundament entzogen wird. Daß etwa Goedel, der die prinzipielle Widersprüchlichkeit mathematischer Systeme gezeigt hat, auch Mathematiker war, geht nicht in ihr Gehirn rein.
Die Schulmathematik sollte sich des weiteren einer anderen Zwiespältigkeit bewußt werden: daß sie einerseits das (in einseitigem Sinne) einfachste, weil logischste aller Fächer ist; daß sie andererseits aber auch einen enormen Fundus von (oftmals auch primär außermathematischen) Techniken verlangt: sie baut eiskalt aufeinander auf, und wer einmal z.B. die Bruchrechnung (und damit meine ich noch eher die Anschaulichkeit der Brüche als die Rechentechniken) nicht mitbekommen hat, wird bis ins Abitur seine Schwierigkeiten behalten. Oder sie verlangt eben erstmal rundweg Außermathematisches, nämlich z.B. absolute Ordnung (als Herrschaftsziel "Zucht und Ordnung"?: "Sekundärtugenden, mit denen man auch ein KZ betreiben kann").
Man mache sich doch mal klar (weil man es als Lehrer allzu schnell vergißt; eben auch, wie man sich selbst mal damit gequält hat), was für ein Riesenbatzen an vielfältigsten, aus dem Nichts hervorzuholenden Kenntnissen von einem 8-Kläßler verlangt wird, wenn er etwa folgenden (durchaus nicht unüblichen) Term vereinfachen soll:
3· (![]() x -
x - ![]() y)2 - ( -
y)2 - ( -![]() x + 4y)(x - 2) (- 5)
x + 4y)(x - 2) (- 5)
Da wird man doch das Gefühl nicht los, solch ein Term wurde weniger dazu geschaffen, alle nötigen Techniken abzufragen, als dazu, Schüler hereinzulegen.
Auch scheint mir, daß solche Terme wie auch Termumformungen weit über den kognitiven Fähigkeiten eines durchschnittlichen 8-Kläßlers liegen (vgl. Piaget).
Es kommt hinzu, daß die übliche Vereinfachung, nämlich - ![]() x2 + 15x + 17 xy - 40y +
x2 + 15x + 17 xy - 40y + ![]() y 2, für einen 8-Kläßler keineswegs einfacher als der Anfangsterm aussieht, sondern vielleicht wegen der komplizierteren Brüche sogar noch schwieriger. Woher sollte er da überhaupt wissen, wo er hin soll? Was an der Beseitigung der Klammern sollte einfacher sein - zumal manchmal die Vereinfachung auch umgekehrt in der Herstellung von Klammern liegt (z.B. beim 1. Binomi: a2 + 2ab + b2 = [a + b]2 )?
y 2, für einen 8-Kläßler keineswegs einfacher als der Anfangsterm aussieht, sondern vielleicht wegen der komplizierteren Brüche sogar noch schwieriger. Woher sollte er da überhaupt wissen, wo er hin soll? Was an der Beseitigung der Klammern sollte einfacher sein - zumal manchmal die Vereinfachung auch umgekehrt in der Herstellung von Klammern liegt (z.B. beim 1. Binomi: a2 + 2ab + b2 = [a + b]2 )?
Der Eindruck ist nicht neu: wenn 8-Kläßler sowas rechnen, so oftmals ohne Sinn und Verstand (und doch oft mit gewisser Logik und oftmals auch echtem Bemühen). Und selbst für die "guten" Mathematiker unter ihnen gilt oftmals, daß sie sehr wohl die Rechenverfahren beherrschen, ansonsten aber auch für sie gilt: "denn sie wissen nicht, was sie tun". Ein Teil dieser "guten" Mathematiker haben zudem eine (perverse?) Vorliebe für (sinnlose?) Knobeleien, ja, man wird das Gefühl nicht los, sie sind die Stumpfsten von allen, man könnte sie an die allerletzte Sträflingsarbeit setzen (Kreuzworträtsel, Puzzles aus 5000 Teilen). Ist es da nicht viel "gesünder" und "kreativer", solch stumpfsinnige Termumformung schlichtweg zu verweigern?
(Es sei eingeschoben, daß solche etüdenhaft langweiligen Termumformungen gar nicht zu vermeiden sind [weshalb ich auch skeptisch gegen den grundsätzlichen Einsatz neuester Computer, die sowas längst auch beherrschen, in der Schule bin]: z.B. mittels Termumformungen lernt, ja paukt man nunmal die handwerklichen Techniken, die man später für einen souveränen Umgang mit Mathematik braucht; nur kennen die Schüler ja noch nicht dieses Fernziel, haben also keine Motivation auf es hin. Und ich werde auch das Gefühl nicht los, daß die Kreativität oftmals schon mittels ihrer stumpfen Vorarbeiten totgeschlagen wird. Wer soll da später noch an der "richtigen" Mathematik Spaß haben?
Mathematik kann nicht immer anschaulich und spaßig sein - und sollte es doch wo immer möglich sein.)
Wie kann man diesen (sicherlich überspitzt dargestellten) Problemen begegnen?:
durch besseres, verständlicheres Erklären;
durch mehr Anschaulichkeit
(Modelle, Wirklichkeitsbezug; der allerdings durchaus problematisch, nämlich oftmals erheblich komplizierter als die Mathematik selbst ist, weil die Wirklichkeit nunmal nicht so eindeutig und so leicht mathematisierbar ist; so zynisch es sich anhören mag: die Schüler sollten fast froh sein, mit Pseudo-Anwendungsaufgaben und Formalkram abgespeist zu werden; es sei schon darauf hingewiesen: dann ist eben die Einfachheit und Schönheit [!] dieser Formelsprache zu vermitteln.)
durch permanente Darstellung der inneren Zusammenhänge der Mathematik (Vor- und Rückverweise)
durch Mitreflexion der gesellschaftlichen Stellung von Mathematik sowie ihrer enormen Leistungsfähigkeit, aber auch der fatalen Begrenztheit ihrer Modellierung
(das - incl. philosophischer Fragen - geht durchaus auch schon in 8. Klassen; und doch ist mir oftmals danach, es aufzugeben und den Schülern nichts mehr vorzuheucheln; ihnen also beispielsweise nicht mehr den Totschläger "non scholae sed vitae discimus" hinzuknallen, sondern dreist zu sagen: "ihr braucht es für schlichtweg gar nichts - außer für die nächste Arbeit, das nächste Zeugnis und das Abitur")
durch Einbringen des historischen Hintergrunds von Mathematik: wie sie immer Kind der Weltwahrnehmung ihrer Zeit war und diese befördert, ergänzt und ausgedrückt hat. Mathematik wird mir viel zu unhistorisch beigebracht: mit dem Effekt, daß sie vielen wie der Hammer Gottes auf den Kopf herabknallt und sie nurmehr erschlägt - und beschämt: "da wäre ich nie drauf gekommen".
durch (wie auch immer) Darstellung der Ästhetik, der inneren Schönheit der Mathematik: wie kann man Schülern das Gefühl eines "richtigen" Mathematikers vermitteln, dem doch jede Anwendbarkeit herzhaft egal ist, der sich doch nur für die immanente Schönheit der Mathematik interessiert, für sie als Selbstzweck?
Wie kann man es schaffen, Staunen dafür zu erwecken, daß die Mathematik in Bereiche vortasten kann, wo keine Anschaulichkeit mehr hinreicht; daß also die Mathematik zum 7. Sinn wird?
Das ist o.g. Frage nach der "kapitalistischen" Unverwertbarkeit und steht damit im Zusammenhang der Diskussion der "lart pour lart", d.h. der zweckfreien Künste und Grundlagenwissenschaften.
Und damit bin ich überhaupt erst beim Thema: Mathematik als eine Form der Künste.
Und doch sei noch etwas eingeschoben: die Punkte 1. - 6. verlangen, so scheint mir, dringend eine Begrenzung des mathematischen Schulstoffs: ich halte es beispielsweise für skandalös, wenn da noch kurz vor dem Abitur ohne Sinn und Verstand, ohne Beweise und Anwendbarkeit e-Funktionen durchgeknallt werden, nur um irgendwelchen Stoffanforderungen der Richtlinien zu entsprechen.
Was ich meine: weniger wäre mehr (und noch lange keine Resignation, kein Einknicken): man muß nun wahrhaft keine e-Funktionen beherrschen, sondern wer die Ableitbarkeit von Potenzfunktionen wirklich verstanden hat, wird gegebenenfalls auch noch die von e-Funktionen verstehen und sich selbst erarbeiten können (und letzteres ist doch eigentlich die zentrale zu vermittelnde Fähigkeit).
Man (als Lehrer) müßte sich an einigen Stellen viel mehr Zeit lassen: einerseits bedarf es sicherlich vieler Beispiele (auch für Ausnahmen: e-Funktionen werden nunmal ganz anders abgeleitet als Potenzfunktionen). Andererseits wäre ich aber für ein erheblich exemplarischeres Vorgehen: wer "nur" den "Pythagoras" und die Wurzeln (incl. Heronverfahren und Irrationalitäts-Begriff) gelernt und wirklich verstanden hat, hat eigentlich alles Wichtige auf der Schule mitbekommen.
Und am Beweis, daß die Wurzel aus 2 irrational ist, kann man Großteile der antiken Philosophie aufhängen! Umgekehrt würde man mit der inzwischen manchmal angedachten Abschaffung des "Pythagoras" auch modernistisch einen Teil der Kulturgeschichte kappen (eben so, wie heute leichtfertig das Fach Latein abgeschafft wird).
Die genannte Frage nach der Zweckfreiheit von Mathematik hat ihre Parallele in allen Künsten. Auch andere Künste schlagen sich immer wieder mit den - wie ich meine - schon grundweg falsch gestellten Fragen herum:
"wozu ist das gut?" - zu nichts (zumindest nicht in einem monokausalen, nachweisbaren Sinn)!
"was will uns der Dichter damit sagen?" - vermutlich gar nichts!
"ich verstehe die Kunst von Beuys nicht" - da ist auch nichts (zumindest im üblichen Sinne) zu "verstehen" (und bei der Mona Lisa auch nicht)!
Was nun aber mag die Ästhetik der Mathematik sein, worin mag sie bestehen?
Dazu vielleicht erstmal einige zweifellos subjektiv und im Hinblick auf die Mathematik ausgewählte Kriterien für Ästhetik (es gibt auch ganz andere Kunstformen):
ein Kunstwerk muß in allererster Linie erfreuen, der Umgang mit ihm muß Spaß machen und anregen;
die Freude liegt oftmals in der Einfachheit im Vergleich mit einer chaotischen Außenwelt;
ein Kunstwerk muß immanent eine harmonische Ordnung, eine Struktur aufweisen (was noch lange nicht eine Bestätigung der gesellschaftlichen Ordnung bedeutet; eigentlich müßig zu erwähnen, daß gerade moderne Kunst oftmals das Gegenteil, die Darstellung des Chaos, ist);
gleichzeitig muß ein Kunstwerk (etwa im Gegensatz zu Trivialliteratur) überraschend sein, zum Staunen anregen;
wahre Kunst besteht im reinen Spiel (laut Schiller ist der Mensch überhaupt erst ganz Mensch, wenn er spielt);
ein Kunstwerk muß offen, d.h. anregend sein;
ein Kunstwerk sollte immer mal wieder eine Selbstbefreiung anstoßen (laut Rilke sagen: "Du mußt [und kannst!] dein Leben ändern"), also einen in den eigenen Fähigkeiten ermuntern;
ein Kunstwerk muß Respekt vor dem Geheimnis behalten, das sein eigentlicher Zweck ist: es umfahrend aufweisen, aber nicht ausplaudern und zerstören;
zuguterletzt ist Zweckfreiheit ja gerade der Inbegriff von Kunst; alles andere ist verdammte Pflicht.
Bevor wir auf diese Kriterien zurückkommen, seien aber noch mit Nietzsche zwei Arten von Lebensform und Kunst unterschieden, die sich wie Jing und Jang ergänzen und abwechseln müssen, ja, überhaupt erst zusammen die Wirklichkeit ausmachen: auf der einen Seite die "apollinische", d.h. verstandesmäßige, auf der anderen Seite die "dionysische", d.h. orgiastische, emotionale, körperliche (und doch ist mir unwohl beim Klischee dieser Trennung: mir scheint noch immer, der Riß verläuft nicht zwischen "Kopf" und "Bauch" - in der Regel wird dann letzterer gegen ersteren ausgespielt -, sondern mitten durchs Herz; die Kopf-Bauch-Trennung scheint mir ein kapitalistischer Kunstgriff, um die Menschen unglücklich und gleichzeitig doch bei der Stange zu halten).
Mathematik gehört, wenn sie denn überhaupt Kunst ist, wohl in die apollinische Kunst. Und doch: auch in ihr, oder genauer: in ihrem Vollzug gibt es dionysische Elemente: da ist jemand "geil" auf die Lösung eines mathematischen Problems, und wenn sie ihm gelingt bzw. überzeugend vorgeführt wird, bekommt er einen "intellektuellen Orgasmus" (mich wundert immer, daß viele kulturelle Leistungen die Menschen so kalt lassen können). Oder von mir aus auch weniger sexuell ausgedrückt und doch sinnlich: da hüpft einem das Herz vor Freude!
Kommen wir damit zur Überprüfung obiger Kunstdefinitionen anhand der Mathematik und fangen wir mit dem allerwichtigsten ersten Punkt an: ein Kunstwerk müsse in allererster Linie erfreuen, der Umgang mit ihm müsse Spaß machen:
Hier wird ausdrücklich von prozeßhaftem Umgang, von "work in progress" gesprochen: Spaß an der Mathematik macht oftmals weniger das Faktum (der erfolgte Beweis) als der Prozeß seiner Entdeckung (daher auch der Spaß am Knobeln): wie bei jedem Kunstwerk mit offenem Ausgang: frustrierendes Scheitern (es sei denn, schon der Prozeß selbst hat einem Spaß gemacht) oder aber Krönung durch ein Ergebnis.
Das impliziert: ich darf nicht nur (wie oftmals wohl in der Schule) fertige Ergebnisse vorgesetzt bekommen ("friß oder stirb"), sondern muß auch eine Chance gehabt haben, sie selbst zu finden oder zumindest selbständig nachzuvollziehen ("als hätt ichs selbst gefunden; sieh mal einer an, ich bin genauso schlau wie Euklid."). Dieser Jubelschrei: "Heureka - ich habs gefunden!"
Nun kann und muß man nicht alles selbst nachentdecken (es ist zu viel, und auf vieles kommen nunmal nur Genies), sondern es ist ja durchaus ein Geschenk, daß unsere Vorfahren es schon entdeckt haben. Aber einerseits ist ihre Mühe zu würdigen, indem man sie (exemplarisch) nachvollzieht, andererseits kann ja dieser Nachvollzug schon spannend genug sein: eine Geschichte der Entdeckung des Limes kann man genauso spannend schreiben wie die Geschichte großer Seefahrer (ich bin fiktiv selbst dabei und Newton bzw. Columbus).
Um Zeit für (Nach-)Entdeckungen zu lassen, müßte Mathematik in den Alltag integriert sein, in ihm wachsen: die "großen" Erkenntnisse entstehen nicht verläßlich im 45-Minuten-Takt der Schule, sondern oftmals abseits, urplötzlich im Alltag. Da beschäftigt man sich mal gerade nicht mit Mathematik, sondern geht z.B. spazieren - und urplötzlich kommt einem die Lösung, der Musenkuß für ein einige Stunden vorher angedachtes, aber damals nicht gelöstes mathematisches Problem.
Zur Ästhetik der Mathematik gehört auch eine gewisse Dramaturgie der Erkenntnis. Was fertig vorgeführt wird und nur noch verkürzt nachgehechelt werden kann, ist aber sicherlich nicht mehr dramatisch. Folge davon ist oftmals, daß die Schüler im besten Fall noch brav rechnen können, erstaunliche Ergebnisse aber überhaupt nicht mitbekommen: sie bemerken beispielsweise gar nicht, wann ein Beweis so wunderbar "zusammenschnurrt", daß also gerade an der Tafel erschien, was man beweisen wollte.
Zur Entdeckung gehört allerdings auch - wie oben schon angedeutet - die Frustrationstoleranz, Etüden durchzuhalten, sowie das Vorhandensein gewissen Handwerkszeugs. Auf jeder Stufe müssen aber auch schon kleine Erfolgserlebnisse vorliegen.
Schon hier zeigt sich: wenn der Prozeß interessant ist, zählt nicht mehr allein die Anwendbarkeit und Brauchbarkeit des Ergebnisses.
Mathematik - wie jede intensive Beschäftigung mit einer Sache - hat auch etwas von Selbstbestätigung (Orgie) nach Selbstüberwindung (Askese). Bei der Mathematik kommt aber noch (vielleicht wie bei Computern) noch was anderes hinzu: es reizt einen, die Sache zu überwinden und zu knacken: "ich lasse mich doch nicht von einem Computer/einer Wurzel beschämen!"
Ja, es ist gerade Aufgabe der Mathematik, die Überlegenheit des Menschen über Computer zu zeigen: bei allem Staunen über Ansätze von K.I. (künstlicher "Intelligenz"), bei allen neuen Möglichkeiten des Computers, die uns noch wahrhaft baß erstaunen lassen werden, ist der Computer bisher doch bloß ein dummer Rechenknecht. Er kann nicht – und das wäre unbedingt zu zeigen -, was jeder 6.-Kläßler kann: mit hantieren (die meisten Computer rechnen noch dezimal, also mit gerundetem und deshalb letztlich falschem 0,333333333), vor allem aber: sich vorstellen.
Spaß kann aber auch das Jonglieren mit der Formelsprache machen. Wir können doch heilfroh sein, daß im letzten Jahrhundert diese abgekürzte Formelsprache entwickelt wurde, die es uns erspart, wie vorher alles in Alltagssprache zu umschreiben.
Kommt hinzu, daß diese Formelsprache den Reiz einer Geheimschrift haben kann, ja, selbst ästhetisch aussehen kann:  oder
oder 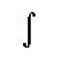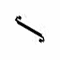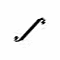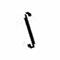 oder
oder ![]() . Oder wie erstaunlich es doch ist, daß viele Ziffern (und auch Druckbuchstaben) symmetrisch sind. Kein Wunder, daß sich die (kabbalistische) Zahlenmystik oftmals in solcher Formelsprache ausgedrückt hat.
. Oder wie erstaunlich es doch ist, daß viele Ziffern (und auch Druckbuchstaben) symmetrisch sind. Kein Wunder, daß sich die (kabbalistische) Zahlenmystik oftmals in solcher Formelsprache ausgedrückt hat.
Aber diese Formelsprache ist nicht (nur) Ausschließungsritual einer verschworenen, arroganten, esoterischen Mathematiker-Clique, sondern auch und geradezu umgekehrt gedacht eine Weltsprache (zumindest der westlichen Kultur). Ja, es scheint mir nichtmal so unsinnig, daß die Pythagoräer auf die Idee gekommen sind, sogar Gott spreche und schaffe in mathematischer Sprache: die Mathematik hat - trotz innerer Widersprüche - etwas irritierend Unumstößliches (vgl. ![]() ).
).
Diese Formelsprache macht das Geheimnis handhabbar - und bewahrt es doch: keine Ahnung, was ![]() ist (irgendwas ganz Schräges; und für sowas Schnödes wie den - pfuideibel: - genäherten Dezimalwert, mit dem nebenbei dumme Computer meist noch rechnen, interessiert sich ein echter Mathematiker eh nicht). Aber welch ein (trotz Bewußtseins um die Folgerichtigkeit der Definition) Erstaunen doch immer wieder, daß
ist (irgendwas ganz Schräges; und für sowas Schnödes wie den - pfuideibel: - genäherten Dezimalwert, mit dem nebenbei dumme Computer meist noch rechnen, interessiert sich ein echter Mathematiker eh nicht). Aber welch ein (trotz Bewußtseins um die Folgerichtigkeit der Definition) Erstaunen doch immer wieder, daß ![]() · , also das Produkt zweier völlig "schräger" Zahlen, exakt gleich simple 4 ist: Mathematiker können so herrlich um die Ecke denken und damit dann doch das Komplizierte so wundersam einfach handhabbar machen.
· , also das Produkt zweier völlig "schräger" Zahlen, exakt gleich simple 4 ist: Mathematiker können so herrlich um die Ecke denken und damit dann doch das Komplizierte so wundersam einfach handhabbar machen.
Oh jadoch, es ist auch Teil der Mathematik und ihrer Ästhetik, sich die Finger nicht schmutzig zu machen und immer um die Sache drumherum zu reden: da gibt es z.B. keine Tangente an eine Parabel, sondern sie wird überhaupt erst als Limes von Sekanten definiert.
Oder es ist doch ein wahres Schauspiel (immer wieder des Staunens würdig), wie da ein durchaus komplexer Beweis in wenigen Zeilen und dazu noch hübsch symmetrisch abschnurren kann.
Ebenso atemberaubend kann es sein, wenn ein Beweis dann zuschnappt, ja, es wird sogar und insbesondere demjenigen so erschienen sein, der ihn als erster geführt hat. Da muß fast das künstlerische Gefühl des Musenkusses aufkommen: daß ein Beweis klappt, kommt einem dann nicht mehr als eigenes Verdienst, sondern als Geschenk vor, als Eingreifen eines Gottes, und man staunt dann immer wieder über die aberwitzige, uneinsehbare, "göttliche" Logik der Mathematik. Z.B. auch dann, wenn nach langer, komplizierter Rechnung mit ebenso komplizierten Zahlen sich am Ende alle Kompliziertheit rauskürzt und urplötzlich (gerade in geometrischen Zusammenhängen) letztlich doch atemberaubend einfache Werte rauskommen.
Ebenso ehrfurchtgebietend ist aber auch das Umgekehrte: daß sich im einfachsten geometrischen Zusammenhang schon ir-rationale Zahlen ergeben (z.B. ist die doch eigentlich sehr simple Diagonale eines quadratischen Tischs der Seitenlänge 1 Meter merkwürdige ![]() m = 1,4142undsoweiterund(ebennicht)sofort Meter lang: solch eine irrationale Zahl, die hinter dem Komma unendlich weitergeht und nie periodisch wird, hat doch geradezu das Eigenleben einer Schlange: sie setzt sich auch noch an der hundertsten und tausendsten Stelle hinter dem Komma fort - ohne unser Einsehen, unabhängig von unserem Einsehen. Sie ist wie ein Kind, das wir vielleicht noch gezeugt haben, dessen weiteres Leben für uns aber uneinholbar ist.
m = 1,4142undsoweiterund(ebennicht)sofort Meter lang: solch eine irrationale Zahl, die hinter dem Komma unendlich weitergeht und nie periodisch wird, hat doch geradezu das Eigenleben einer Schlange: sie setzt sich auch noch an der hundertsten und tausendsten Stelle hinter dem Komma fort - ohne unser Einsehen, unabhängig von unserem Einsehen. Sie ist wie ein Kind, das wir vielleicht noch gezeugt haben, dessen weiteres Leben für uns aber uneinholbar ist.
Die Bezeichnung "irrational" bewahrt ja auch - obwohl doch erstmal abwertend gemeint - diesen metaphysischen Aspekt.
Überhaupt scheint mir, daß ein "richtiger" Mathematiker sich das Staunen über sowas bewahren, also beispielsweise den Begriff der Irrationalität noch keineswegs für ausgemacht halten sollte. Man sollte sich das Staunen über die Paradoxie bewahren, daß die Tischdiagonale immer gleichlang bleibt, die Zahl dafür aber wie ein Rattenschwanz immer länger wird und doch einen bestimmten Wert nie übersteigt.
Solches Staunen sollte man sich auch über Beweise bewahren: der Stumpfmathematiker wundert sich über Beweismöglichkeiten schon gar nicht mehr und lehnt überhaupt alles ab, was nicht mathematisch beweisbar ist. Dabei funktionieren Beweise doch ganz anders: sie sind im Grunde der Inbegriff des Selbstzwecks: da werden vollständige Induktionen oder Widerspruchsbeweise oftmals doch nicht durchgeführt, um einen neuen Sachverhalt zu beweisen, sondern um nur anhand des neuen Sachverhalts immer wieder das uralte, noch immer staunenerregend unverständliche Beweisverfahren zu feiern.
Wie ästhetisch Beweise sein können bzw. wie lange oft nach einer besonders ästhetischen Beweisversion gesucht wurde (obwohl doch das entsprechende Faktum längst bewiesen war), aber auch, was eigentlich an dürren mathematischen Beweisen ästhetisch sein kann, zeigen Martin Aigner und Günter Ziegler an vielen Beispielen in ihrem Buch "Proofs from THE BOOK".
Überhaupt kriegt sich ein "richtiger" Mathematiker oftmals gar nicht ein über die Fähigkeiten der Mathematik: daß sie die einzige Wissenschaft ist, die absolute und allgemeingültige Beweise führen kann (lassen wir hier mal Goedels Problematik weg). Z.B. - oh wie unfaßbar erstaunlich - in wenigen (endlich vielen) Zeilen, daß alle (und mindestens ebenso erstaunlich: unendlich viele) Dreiecke die Winkelsumme 1800 haben. Wohlgemerkt: exakt 1800 Grad und keinen Hauch weniger oder mehr; und wieso eigentlich exakt das Doppelte des rechten Winkels - und wieso wiederum ist ausgerechnet der so wichtig und dominant? Gerade weil ich nicht alle (unendlich viele) Dreiecke überschauen kann, bleibt all das doch eine höchst erstaunliche Angelegenheit.
Oder wie unfaßbar es doch ist, daß man gerade ausgerechnet an einer einzigen hingeworfenen Planskizze allgemeingültige Beweise führen kann, weil die Planskizze in unserem Kopf platonisch idealisiert wird. Daß der Mensch zu sowas fähig ist!
Ein anderes Beispiel: es läßt sich beweisen, daß wahrhaft jedes Dreieck (also etwas Gerad-Eckiges) einen genau passenden In- und Umkreis (der Inbegriff des Runden) hat:
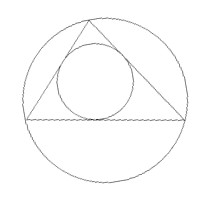
Die Beweise dazu sind durchaus einsehbar (allerdings: woher "wußten" das Dreieck und die Kreise, daß sie über die Winkelhalbierenden bzw. Mittelsenkrechten zusammenhängen - oder sind das nur die Beweiskrücken unseres eingeschränkten menschlichen Geistes?). Und doch mag mans nicht recht glauben: zumindest der Laie wird doch denken: aber das funktioniert doch wohl nicht mehr für ein ganz aberwitzig schmales Dreieck, z.B.

Oh doch, auch da funktionierts!:
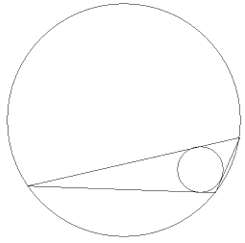
Und doch bleibts auch für einen richtigen Mathematiker - trotz Beweises - wenig überzeugend: man kommt nicht ganz drumherum, fast schon hämisch zu hoffen, daß sich irgendwo unter all den unendlich vielen Dreiecken mal ein besonders keck-vorlautes melden wird, das keinen In- und Umkreis hat und somit den Mathematikern mal zeigt, was eine Harke ist. Der Beweis, daß es solch ein Dreieck nicht geben kann, bleibt wenig überzeugend, ja, enttäuscht so gesehen sogar ein wenig. Kein Wunder, daß einige Spinner (?) beispielsweise noch immer versuchen, die Quadratur des Kreises herzuleiten, sich also durch den längst geführten (allerdings für solch ein äußerlich einfach aussehendes Problem doch geradezu verdächtig schwierigen) Beweis, daß diese nicht möglich ist, nicht beschämen lassen wollen (genau genommen haben sie den Beweis wohl nie verstanden, ja, nie eine Chance gehabt, ihn zu verstehen). Zudem liegt die Quadratur des Kreises doch nahe, wenn man erstmal wie oben die Verwandtschaft von Geradem (Dreieck) und Rundem (Kreis) gesehen hat.
Und es bleibt auch staunenswert, daß Gerades und Eckiges sich überhaupt so wundersam vermählen können (die Winkelhalbierende als ein Kind der Liebe?). Es kommt einem fast vor, als hätte Gott im Himmel ein Dreieck und einen Kreis zur Hochzeit prädestiniert. Wie anders wäre es zu erklären, daß sie sich ausgerechnet in obiger Zeichnung treffen?
Nun ließe sich – immer schon ziemlich abstrakt – jeweils beweisen, daß
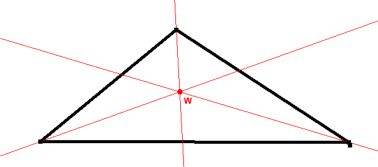
alle drei Winkelhalbierenden (die Halbgeraden jeweils genau in der Mitte eines Dreieckswinkels) jedes Dreiecks sich in einem Punkt W schneiden:
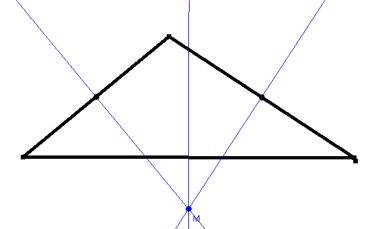
auch alle drei Mittelsenkrechten (senkrecht zur Mitte jeder Dreiecksseite) jedes Dreiecks sich in einem Punkt M schneiden:
auch alle drei Höhengeraden (senkrecht zu einer Seite [oder deren Verlängerung] und durch den gegenüberliegenden Eckpunkt) jedes Dreiecks sich in einem Punkt H schneiden:
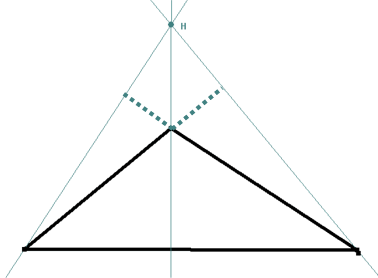
auch alle drei Seitenhalbierenden (von der Mitte einer Seite zum gegenüberliegenden Eckpunkt) jedes Dreiecks sich in einem Punkt S schneiden (der nebenbei – wie auf den ersten Blick doch immerhin überraschend - der Schwerpunkt des Dreiecks ist):
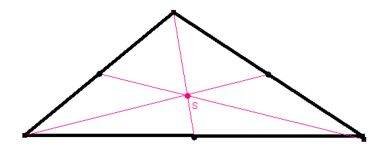
Ich finde schon a), b), c) und d) jeweils für sich genommen umwerfend erstaunlich. Noch erstaunlicher finde ich, daß a) – zudem mit dem Inkreis – und b) – zudem mit dem Umkreis – und c) und d) – zudem mit dem Schwerpunkt – in einem Dreieck gleichzeitig funktionieren. Fast würde ich sagen: "woher wußte beispielsweise die erste Winkel- von der letzten Seitenhalbierenden?". Und all das nicht nur bei einem speziellen Dreieck oder einigen wenigen Dreiecken, sondern bei ausnahmslos allen (es muß letztlich alles auf das "Dreieck-Sein" zurückführbar und von Anfang an in und mit ihm angelegt sein).
Am umwerfendsten ist es aber, daß (ein kleiner Schönheitsfehler, der die vollkommene Harmonie doch ein wenig stört) zwar nicht der Punkt W, wohl aber die Punkte M, H und S zwar nur in gleichseitigen Dreiecken zusammenfallen, aber - natürlich bzgl. ein und desselben Dreiecks - immer (oder genauer: außer eben bei gleichseitigen Dreiecken) auf einer Geradeng liegen:
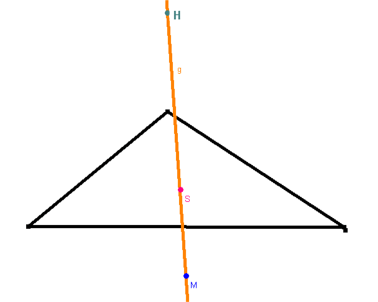
Das ließe sich natürlich beweisen, aber dieser Beweis wäre doch aufgrund der vielen Einzelschritte letztlich völlig unanschaulich - und vielleicht finden wir die Tatsache, dass die Punkte M, H und S alle auf einer Geradeng liegen, gerade deshalb so ästhetisch.
Die rein innermathematische Schönheit erscheint einem da als Spiegel einer höheren, fast hätte ich gesagt: "esoterischen" Ordnung, nur daß dieses Jenseits ausschließlich aus mathematischen Elementen besteht, die für "belebt" und intelligent zu halten zwar ein wichtiger Effekt ab und zu, letztlich aber natürlich unsinnig ist (vgl. ![]() ).
).
Ich frage mich, ob da versehentlich (d.h. verständlich, aber ohne tatsächliche Bedeutung) sogar eine moralische Ordnung vorausgesetzt wird. Ist es ein Zufall, daß der (ist das vielleicht wichtig?: japanische) Mathematiker Shimura erst von "gut" spricht – und es, als ihm vielleicht bei solch moralischer Sprechweise angst und bange wird, dann doch nur auf "ästhetisch" zurückführt?:
"Ich vertrete diese Philosophie des Guten. Die Mathematik sollte das Gute enthalten. So kann man im Falle der eliptischen Gleichung sagen, sie sei gut, wenn sie von einer Mudulform parametrisiert wird. [...] Ich könnte sagen, daß diese Vermutung der Philosophie des Guten entsprang. Die meisten Mathematiker betreiben Mathematik von einem ästhetischen Standpunkt aus, und diese Philosophie des Guten rührt von einem ästhetischen Standpunkt her."
Vielleicht liegen ja Moral und Ästhetik tatsächlich gar nicht so weit auseinander: "schön und gut" bzw. laut Goethe "das Schöne, Gute und Wahre" ist, was die Harmonie (nicht zu verwechseln mit Friedhofsruhe) nicht stört, also nicht in Mord und Totschlag führt.
An diesem "Auf-einer-Gerade-Liegen" scheiden sich, so würde ich fast meinen, die Geister:
der Nicht-Mathematiker (oder genauer: der nicht mathematisch Denkende) wird sagen: "schön und gut, aber was solls?" D.h., ihm fehlt das Gespür für mathematik-immanentes Staunen, und er fragt immer nur nach Anwendbarkeit (vermutlich auch bei Kunst);
der Mathematiker (oder genauer: der potentiell und intuitiv mathematisch Denkende, auch wenn er keinerlei formale mathematische Ausbildung hat) aber kriegt sich gar nicht mehr ein vor Staunen: ein eventueller formaler Beweis ergänzt ihm zwar dieses Staunen, untergräbt es aber nicht;
und dem Dumm-Mathematiker ist alles Staunen schon längst wieder abhanden gekommen, der verwechselt den Beweis mit Anschaulichkeit: "da gibts doch gar nichts mehr zu staunen, denn es ist doch bewiesen".
Aber zurück zu den Standardbeweisverfahren: die Mathematik ist also nicht bloß eine Kunst, sondern auch ein Ritual. Warum wohl sind so unendlich viele Beweisverfahren beispielsweise für den Satz des Pythagoras entwickelt worden - und werden vermutlich noch immer neue entdeckt, obwohl er doch längst bewiesen ist? Schlicht und einfach, weil ein richtiger Mathematiker noch gar nicht fassen kann, daß dieser Satz überhaupt gilt.
Dieses Staunen geht daraus hervor, daß ein "richtiger" Mathematiker keineswegs weltblind ist, sondern sehr wohl weiß, daß solche allgemeine Beweisbarkeit die absolute Ausnahme ist.
Ein anderer Grund, den "Pythagoras" immer und immer wieder zu beweisen, ist es sicherlich, kürzere und elegantere, also ästhetischere Beweise zu finden.
Ich z.B. finde den Beweis über Scherungen und Drehungen (also harmonische Bewegungen!) nach wie vor erstaunlich schön und harmonisch wie eine Welle, wie eine Brandung:
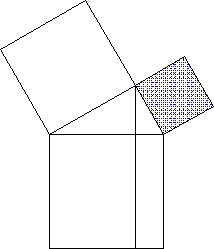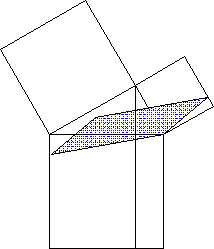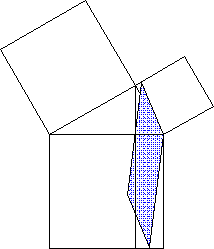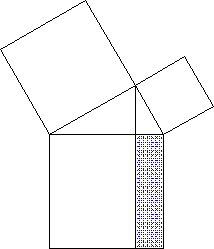
Überhaupt passen solche Metaphern durchaus auch auf die Mathematik: ein schöner, gelungener Beweis hat sowas wie eine Dramaturgie, er fließt wie eine Symphonie (incl. Begleitstimmen, d.h. Nebenrechnungen) oder ein vielfältig strukturiertes und anklingendes Gedicht, er pulsiert wie das Herz, zieht sich zusammen und wieder auseinander (retardierendes Moment) - und am Ende positiv erschütternd (!) wieder zusammen. Das typische "q.e.d" = "quod erat demonstrandum" = "was zu zeigen war", das nach einem erfolgten Beweis oftmals so arrogant hingeknallt wird und jene beschämt (beschämen soll?), die den Beweis nicht verstanden haben, bedeutet doch - gerade in seiner rasanten Kürze - auch: "unglaublich, Volltreffer!"
Ich kann beispielsweise nach wie vor über den klassischen Widerspruchsbeweis dafür, daß die ![]() irrational ist, nur staunen: da hat man ganz am Anfang eher versehentlich (?) was vorausgesetzt (daß der Bruch, durch den man
irrational ist, nur staunen: da hat man ganz am Anfang eher versehentlich (?) was vorausgesetzt (daß der Bruch, durch den man ![]() darzustellen versucht hat, vollständig gekürzt ist), worauf hinterher der gesamte Beweis zuläuft bzw. zusammenschnurrt.
darzustellen versucht hat, vollständig gekürzt ist), worauf hinterher der gesamte Beweis zuläuft bzw. zusammenschnurrt.
Oder ist dieser Widerspruchsbeweis nicht doch ein (typisch) tolldreist raffitückischer Ausweg der Mathematiker aus ihrer Unwissenheit?: weil sie nicht beweisen können, daß etwas gilt, beweisen sie einfach, daß das Gegenteil nicht gilt (lassen wir hier mal das Problem des dann noch fehlenden Existenzbeweises weg: nur weil Erwin kein Schwarzer ist, ist er noch lange nicht ein Weißer, sondern kann auch ein Indianer oder auch schlichtweg irreal-erfunden sein).
Das alles ist natürlich einfach nur Spiel: ein richtiger Mathematiker ist und bleibt nichts anderes als ein Spielkind: "wenn ihr nicht werdet wie die Kinder". Selbstverständlich ist Mathematik nicht mehr als ein Modell, vergleichbar durchaus einem Eisenbahnmodell: da kann "das Kind im Manne" endlich nach eigenem Gutdünken und rein fiktiv (wie in Kunst!) schalten und walten, da quatscht ihm keiner (außer der Logik der Sache) rein. Deshalb halte ich ja auch die erwachsene Ernsthaftigkeit und Wichtigtuerei von Mathematikern (und allemal von Nichtmathematikern an die Mathematik herangetragen) für so schlimm: Mathematik ist keineswegs das wichtigste Schulfach, und es wird erst frei, wenn es nicht mehr als solches angesehen wird bzw. sich so aufplustert.
Mathematik ist auch eine Form der Meditation: es bleibt sich gleich, ob man einen Matheaufgabenzyklus löst, Zen-Buddhismus oder Rosenkranzbeten betreibt.
Und Mathematik ist oftmals auch so herrlich einfach, bzw. der Spaß kommt überhaupt erst, wenn man das plötzlich "rafft". Ich erinnere mich noch an den Augenblick, in dem für mich die Funktionentheorie an der Uni verständlich wurde: "ach, so ist das also: erst leitet man 50 Seiten lang die Holomorphie her (was für ein schön kryptisches Wort!), und dann feiert man 300 Seiten lang, was sich damit so alles anstellen läßt". Oder die SchülerInnen so schwierig zu vermittelnde Beweisart der vollständigen Induktion ist doch im Grunde so einfach: die erste Ampel ist grün, und wenn eine Ampel grün ist, dann ist auch die nächste grün. Das Ganze nennt man "grüne Welle"!
Mathematik ist einfach, ja, das simple Denken führt oftmals überhaupt erst zum Ziel. Newtons und Descartes Geniestreich lag doch vermutlich darin, daß sie gedacht haben: "mit Schrägem (Graphen, Flächen) kann ich nicht umgehen, dazu bin ich zu doof; also versuche ich mal den Umweg über Gerades [Tangenten, Rechtecke]". Und dieser Umweg führte nicht nur auch zum Ziel, sondern war selbst wieder schön (die geometrische Abfolge der Iterationsverfahren) - und bewahrte doch gleichzeitig das Geheimnis des Krummen. Ja, er adelte das "krumme Holz".
Am allerschönsten aber ist wohl der Augenblick, wo einem selbst ein Beweis gelingt. Das funktioniert, wie ich es manchmal auch meinen SchülerInnen sage: man muß nicht Mathematik können, man muß überhaupt nichts Bestimmtes, Anerkanntes können (Goethe und die Bibel gelesen haben); aber man sollte ein Gebiet haben, auf dem man was kann, auf dem man Selbstbestätigung erfährt (auch ohne die Anerkennung anderer Menschen). Ein gelungener eigener mathematischer Beweis sagt mir letztlich doch nur: "du kannst was - also auch auf anderen Gebieten.": "steh auf, kein Knochen ist dir gebrochen, kein Haar gekrümmt!"
Richtige Mathematik bleibt immer offen (also genau das Gegenteil von einem erschlagenden "Hammer Gottes"): die Fülle des mathematischen Wissens explodiert nach wie vor, Mathematik ist in ihrer Avantgarde immer erstmal unanwendbar - und erst 50 Jahre später kommt ein Physiker, der eine gewisse mathematische Theorie gebrauchen kann.
Offenheit auch noch im anderen Sinne: es ist doch einfach nur herrlich, daß den Billigmathematikern ihre Eindeutigkeit abgegraben wird: durch jene von Goedel gezeigte Widersprüchlichkeit, durch Wahrscheinlichkeits- und Chaostheorie sowie durch vielwertige (sogar stetig verteilte, "verschmierte") Fuzzy-Logik: in zweiwertiger Wahr-Falsch-Logik zu denken, ist mindestens ebenso blödsinnig und nicht mehr ernst zu nehmen wie Menschen, die entweder fanatisch religiös gläubig oder aber - genauso dämlich - fanatisch atheistisch sind (und in der Tat: viele Billigmathematiker sind auch über die Mathematik hinaus meist ein- bis höchstens zweidimensional). Die Auflösung solch zweidimensionaler Wahrhaftigkeit empfinde ich geradezu als die Nacht der langen Messer, die Rache der Entnervten (und überhaupt war die Avantgarde der Mathematiker und Naturwissenschaftler immer erheblich philosophischer und vieldeutiger als all ihre Epigonen - und alle Vorstellungen, die sich "der kleine Mann" heutzutage von Mathematik und Naturwissenschaft macht).
In gewissem Sinne ist Mathematik auch - wie schon angedeutet - metaphysisch. Erst z.B. die riemannsche Geometrie hat Einstein das mathematische Handwerkszeug zur Verfügung gestellt, unsere Anschauung zu überschreiten. Und da mag man sich (gerade große Physiker haben das immer getan) bewußt bleiben, daß alles nur Theorie ist, man also "Gott" (den "Dingen an sich") niemals auf die Schliche kommen wird; gleichzeitig liefert es aber eben doch das Gefühl, ihm ein bißchen mehr auf die Schliche gekommen zu sein. Das ist nicht bloß Arroganz, sondern "Gott" hat ja laut Bibel den Menschen nach seinem Ebenbild geschaffen.
Wie gesagt, solche Mathematik bleibt unanschaulich und ist somit Teil unserer manchmal entnervend abstrakten und unsinnlichen (und damit unsinnigen?) Kultur. Gleichzeitig passiert da aber doch auch etwas absolut Wunderbares:
Grenz-, Selbst- und Sinnlichkeitsüberschreitung;
Staunen über die Denkfähigkeit des Menschen über sich hinaus;
Staunen darüber, daß der Mensch das Universum (teilweise) durchschauen und erklären kann, daß er also Zentrum seiner Welt bleibt (wie schon Kopernikus sagte: er wolle mit der Erde nicht auch den Menschen aus dem Mittelpunkt des Universums vertreiben, sondern im Gegenteil bleibe er ja gerade durch seine Erkenntnisfähigkeit Mittelpunkt); dieses Staunen ist aber keine anthropozentrische Arroganz, sondern entsteht aus und endet in Dankbarkeit;
Staunen auch über "Gott": daß man ihm so hochkomplex und doch verwirrend einfach auf die Schliche kommt, erhöht ja nur das Staunen über seine Schöpfung - und die "Andacht";
Staunen immer wieder darüber, daß die Mathematik überhaupt und eben doch anwendbar ist: daß der freie Fall beliebt, sich exakt nach der Formel s = ![]() gt2 zu richten! Oder haben wir - und wenn ja: wie? - der Natur die Mathematik abgeguckt?
gt2 zu richten! Oder haben wir - und wenn ja: wie? - der Natur die Mathematik abgeguckt?
Staunen aber auch über die theoretisch-philosophischen Hinter- und Abgründe, die sich da auftun: ob wir Menschen (wo wir nunmal evolutionär darauf getrimmt zu sein scheinen, in alles Muster reinzusehen, weil wir sonst gar keine Ordnungsmuster hätten) da nicht eben doch nur unser System in die Natur projizieren: ja und, dann sind wir erst recht ihre Herren!
Staunen über den inneren Automatismus von Mathematik (beispielsweise bekam Einstein anfangs mathematisch raus, das Weltall expandiere - und hat das dann erstmal nicht glauben wollen und fälschlich durch eine selbstherrlich eingefügte Konstante getilgt).
Das hier immer wieder angedeutete Staunen erscheint mir enorm wichtig, ja, fast als Rettung unserer Kultur. Wie schön, daß Physiker noch immer nicht erklären können, was ein elektrisches Feld (Metapher!) eigentlich ist und wie genau es zustande kommt. Irgendwann wird das vielleicht jemand schaffen - aber dann bleibt ein anderes Geheimnis über oder ergibt sich überhaupt erst ein neues. Z.B. scheinen die bislang kleinsten Elementarteilchen, die Quarks, neuerdings eben doch nochmal teilbar zu sein. Hurra!
Und es freut mich doch in aller Genüßlichkeit - da bin ich mal Prophet -, daß bestimmten arroganten und anmaßenden Physikern und philosophischen Dummschwaflern die anvisierte "große Vereinheitlichung" garantiert nicht gelingen wird. Solchen Schwachköpfen ist "Gott" ja glücklicherweise doch noch um einiges voraus!
Wie langweilig wäre es auch, wenn wir mit unserer Erkenntnis irgendwann am Ende wären (mal abgesehen davon, daß gerade Mathematiker wie z.B. Chaitin bewiesen haben, daß das nie geschehen wird). Was ja nicht ausschließt, daß der Versuch vollständiger Erkenntnis immer wieder gemacht werden wird; schon allein, weil das Unbekannte beängstigend ist.
Mathematik wie Technik müssen einen eben nicht erschlagen: es ist und bleibt doch geheimnisvoll erstaunlich, ja, kann einen geradezu mit (positiv gemeint:) demütiger Dankbarkeit erfüllen, daß überhaupt jemand die Elektrizität entdeckt hat - und so viel mit ihr funktioniert.
Mathematik ist noch in anderem, viel anschaulicherem, ja sinnlicherem Sinne Kunst: z.B. eine Kugel (man schaue sich mal die Faszination der Menschen für Kugeln an, die auf jedem zweiten Nippesregal rumliegen und als "Kunst am Bau" unsere Städte verschandeln!) ist sogar mathematisch nachweislich besonders "schön": sie ist - im geistigen Rausch der Analysis (diesem Megageniestreich Newtons und Leibnizens aus purer Verlegenheit heraus) nachweisbar! - der Körper mit kleinster Oberfläche bei vorgegebenem Volumen. Anders gesagt (und so simpel und gleichzeitig doch enorm erstaunlich ist oftmals die Übertragung von rein Innermathematischem auf die Außenwelt): aus Umweltschutzgründen (Materialersparnis) wäre es an der Zeit, alle Milchverpackungen kugelförmig zu machen (eine andere Frage wäre da, wie das herzustellen wäre - und außerdem würde einem die Kugel immer aus dem Kühlschrank rollen und würde es Stapelprobleme setzen; nebenbei sei erwähnt, daß das so einfach aussehende Problem, Kugeln möglichst platzsparend zu stapeln, mathematisch seit Kepler ungelöst ist).
Fast möchte ich sagen: wie schön, daß eine Kugel nicht nur ästhetisch so ansprechend ist (etwa, ganz sinnlich, als Handschmeichler), sondern daß sich das auch noch mathematisch wenn schon nicht absegnen bzw. überhaupt erst legitimieren, so doch betonen läßt.
Was war eher: das Ei oder die Henne? Die mathematische Formel für den goldenen Schnitt - oder daß die alten Griechen beispielsweise Tempel, die nach dem goldenen Schnitt gebaut waren, als so schön empfanden (und es dann nur mathematisch fassen und herstellen konnten)?
Ein weiteres ästhetisches Beispiel sind die Graphen von Funktionenscharen, insbesondere, wenn sie nacheinander entstehen, sich also langsam schließen oder entfalten:
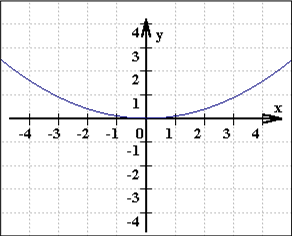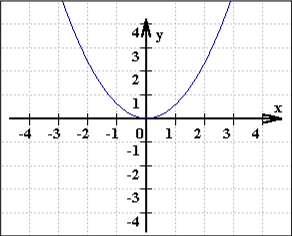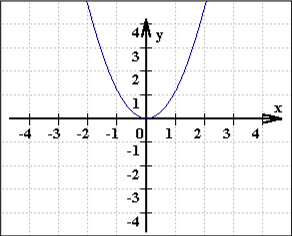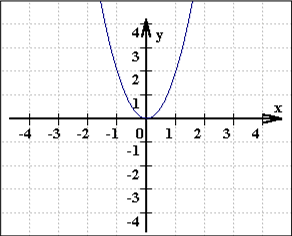
Erinnert das nicht - besonders, wenn es nacheinander, also fast in Bewegung entsteht - an die Zeitlupenaufnahme einer sich langsam öffnenden Blume? (Eine Blume aber ist viel mehr, lebt und duftet nämlich.)
Zumindest für mich, der ich ein ausgesprochen optisch-räumlicher Lerntyp bin und alles nur in Geschichten be-greife, muß sich Mathematik, wenn irgend möglich, bewegen. Und mir scheint: Lerntypen wie mir enthält man wirklich eine Verständnismöglichkeit vor, wenn man ihnen etwa bei der Scherung nur Anfangs- und Endzustand vorführt (vgl. ![]() "jeder auf seine fa&ccdil;on").
"jeder auf seine fa&ccdil;on").
Oft kann man sagen: es gibt nicht nur eine Ästhetik der Mathematik, sondern auch eine Mathematik der Ästhetik (oder genauer: ihrer apollinischen Hälfte):
man schaue sich mal an, wie oft sich Kunst spätestens seit der Renaissance der Mathematik bedient hat. Z.B. bei der Herstellung und Konstruktion von Perspektive (die Fluchtpunktperspektive hat ja auch schon wieder was ästhetisches an sich). Das war nicht nur früher so, sondern wird auch heute noch in fast jedem zweiten Film angewandt: die Darstellung einer Hierarchie unter Personen mittels ihrer Anordnung in der Bilddiagonale; die Herstellung und sinnlich eindrückliche Betonung einer Handlungsdramatik durch mathematisch konstruierte optische Dramatik.
Und viele Entdeckungen wie etwa die Galileis oder von Kopernikus waren erstmal nicht experimentell bedingt (die nur ungenau durchführbaren Experimente widersprachen teilweise sogar erstmal ihren Entdeckungen), sondern mathematisch-ästhetisch: es sah erstmal schöner aus - und erst lange Zeit später bestätigten Experimente die neuen mathematischen Erklärungen; so daß ich den Verdacht nicht los werde, daß auch wir heute vieles nur deshalb für richtig halten, weil es mathematisch-ästhetisch ist und damit unwiderstehlich suggestiv wirkt.
Die Töne der Tonleiter liegen auf einer Saite genau in den Verhältnissen ![]() ,
, ![]() ,
, ![]() usw. (woraus die Pythagoräer geschlossen haben, ganze Zahlen und Brüche seien die konstitutiven Elemente der Schöpfung, ja, Gott habe in ganzen Zahlen und Brüchen gedacht). Und was ist die Notenschrift anderes als eine Darstellung einer Melodie in Form eines Funkionsgraphen? (womit nun wahrhaft nicht gesagt sein soll, diese Notation sei schon die Musik und könne sie gar ersetzen). Bereits ein Duett ist dann beschreibbar durch eine dreidimensionale Funktionen"landschaft":
usw. (woraus die Pythagoräer geschlossen haben, ganze Zahlen und Brüche seien die konstitutiven Elemente der Schöpfung, ja, Gott habe in ganzen Zahlen und Brüchen gedacht). Und was ist die Notenschrift anderes als eine Darstellung einer Melodie in Form eines Funkionsgraphen? (womit nun wahrhaft nicht gesagt sein soll, diese Notation sei schon die Musik und könne sie gar ersetzen). Bereits ein Duett ist dann beschreibbar durch eine dreidimensionale Funktionen"landschaft":
Und der "Gag" vieler Gedichte liegt in ihrem Rahmen/ihrer optisch-geometrischen Symmetrie, d.h. dem Versprechen/der Drohung von ewiger Wiederkehr bzw. des Wandels im Gleichbleibenden:
und
Vietnam
und
(Erich Fried)
Und was ist denn (ohne nun den ganzen esoterischen Schmu mitzumachen, der damit oft getrieben wird) Jing-Jang anderes als vollendet harmonische Geometrie - und damit Symbol, ja, Vergewisserung von Harmonie in der Verbindung/Ergänzung der Gegensätze (geometrisch gesprochen - und seit der Antike ein Grundanliegen der Mathematik - der Verbindung von Geradem und Rundem; vgl. die Quadratur des Kreises).
Wir alle sind (gerade ästhetisch) Mathematiker bis auf die Knochen. Vielleicht nicht von Natur aus, aber sicherlich kulturell so geprägt.
Und teilweise sind wirs geradezu schmerzlich, ist diese geometrische Ästhetik ein kahles Gefängnis geworden: man schaue sich beispielsweise mal die Diktatur des rechten Winkels in unserem Alltag an (und überhaupt die Unmenschlichkeit heutigen Einheits-Designs). Mehr noch: die industriell gefertigten Gegenstände unseres Alltags sind von solch perfekter Glätte, daß sie auf geradezu unheimlich-unmenschliche Art mit den platonischen Ideen (z.B. der Idee eines perfekten Kreises) eins geworden zu sein scheinen (auf die Idee, hinter den "unreinen" Dingen steckten perfekte Ideen, konnte ja vielleicht nur kommen, wer noch nicht perfekte Dinge kannte).
Die Dinge in ihrer Perfektion beschämen uns, zeigen uns immer mehr, wie eben nicht perfekt wir selbst sind (es sei denn, wir versuchen uns verzweifelt den Dingen anzupassen, indem wir etwa kein Körper mehr sind, sondern einen body haben). Und mir scheint auch: solche Dinge sollen uns beschämen: Bankbauten in Frankfurt sind die fast schon faschistoide reine Arroganz der Macht und sollen den Menschen ihre Nichtigkeit zeigen.
Andererseits aber kann man sich ja auch mal das Staunen über die geometrische Perfektion der Dinge bewahren bzw. immer mal wieder hervorholen. Es ist eben nicht so selbstverständlich, daß jedes Plexiglas-Kunststoffschächtelchen, das heute für 20 Pfennig aus der Maschine fällt, so wundersam und faszinierend perfekt ist (die Antike hätte es zum 8. Weltwunder erklärt!). Und wer streichelt nicht gerne glattes Plexiglas? Die Dinge sind - gar nicht mal nur negativ gemeint - göttlich geworden: Roland Barthes hielt es für keinen Zufall, daß der wirklich besonders gelungene Citroen DS eben "DS" hieß: "DeeSse" = franz. "Göttin".
Alle Mathematik ist menschlich, weil sie eben von Menschen geschaffen wurde. Aber Mathematik kann noch viel näher als üblich an den Menschen und die vielfältige Natur ran, seis mittels konventioneller euklidisch-abstrakt-abgenagter Geometrie

seis mittels neuerer fraktaler Geometrie, die die Diktatur des Lineals, das eh nur 1 % der Wirklichkeit beschreiben kann, beenden will:

So – im Vergleich mit üblicher Linien-Mathematik! – erstaunlich dieses Bild (und allemal in Animation) sein mag: es ist doch erstmal nur ein "geiler" Computereffekt (und damit noch lange keine Kunst), hinter dem eine Menge hochkomplizierter Mathematik steckt.
Und "Mathematikerkunst" à la Escher ist natürlich gar keine Kunst, sondern nur ganz billig "tricky": zieht man die optischen Täuschungen und mathematischen Konstruktionsprinzipien ab, bleibt nichts mehr übrig: das ganze Haus ist witzlos, es dient nur als Fundament der unendlichen Dachtreppe.
Die höchste Ästhetik der Mathematik liegt für einen "echten" Mathematiker aber nicht in irgendeiner äußeren Schönheit (dass z.B. gewisse Graphen schön aussehen), sondern in einer inneren Eleganz:
wie schon angedeutet: der eines möglichst einfachen, übersichtlichen und doch überraschenden Beweises;
der ästhetischen Struktur der Mathematik (beispielsweise die Querbezüge zwischen verschiedenen Feldern der Mathematik).
Ausgesprochen lesenswert zum Thema:
 | Hans Christian von Baeyer: Das All, das Nichts und Achterbahn; Physik und Grenzerfahrungen; rororo darin das Kapitel "ästhetische Gleichungen" |
PS: