Mathematik

Ich hatte schon in vielen anderen Essays gesagt (beschworen?), dass die Wirklichkeit heutzutage auf Jugendliche herunterknalle wie ein "Betonklotz"   : alles ist erschlagend fertig (nichts bleibt mehr selbst zu tun).

Und doch war die Metapher des Betonklotzes

(und insbesondere das Bild des durch die Witterung schmuddelig gewordenen Betonklotzes)

ungünstig bis geradezu irreführend: der dreckige Betonklotz ist ja nicht gerade schön, und gerade deshalb könnte man ihn immerhin

• mit

Graffitis

versehen oder

• mittels "Streetbranding" (Schablone und Hochdruckreiniger) verzieren:

Viel passender ist ein (perfekter) Edelstahlklotz : so ca. einen Kubikmeter sollte er schon groß sein und mehrere Tonnen wiegen, also, wenn er auf einen herabfällt, einen verlässlich plätten.

(Nebenbei: es scheint ja Mode zu werden, sogar im Grab noch mit einer 3 x 3 m großen, perfekt polierten Grabplatte geplättet werden zu wollen:

  )

"Zu meiner Zeit" war das noch anders: zwar habe ich, obwohl ich "nur" 14 Jahre nach dem Zweiten Weltkrieg geboren bin, in meiner Kindheit eine da schon wieder erstaunlich heile Welt erlebt, aber ich kann mich beispielsweise doch noch an etwas erinnern, was heutzutage schier undenkbar ist: nicht-asphaltierte Straßen ohne plattierte Gehwege. Entsprechend erscheint mir heutzutage die ganze (?) Welt geradezu edelstahl- bzw. granitmäßig poliert - und pflegeleicht versiegelt:

(die armen Bäumchen!)

(Gibt es etwas Öderes als typische städtische Einfallstraßen: lange Asphaltpisten mit rechts und links nackten Industriebauten und Einkaufszentren. Wieso kommt bei solchen Einfallstraßen eigentlich nie jemand auf eine Idee à la , um die grauenhaft tote Ödnis zu beleben oder zumindest doch zu kaschieren?)

Insbesondere habe ich die glatte Fertigkeit vielfach in der Schulmathematik beklagt, wobei das Problem vielleicht darin besteht, dass die Mathematik gar nicht anders kann:

• ihre "Sätze", einmal bewiesen, gelten ab da in alle Ewigkeit und allgemeingültig.
• Kommt hinzu, dass viele Beweise derart raffiniert sind, dass wohl nur große Genies sie aufstellen konnten, ein Normalsterblicher (Lehrer oder Schüler) sie also im besten Fall nur noch "geleitet nachentdecken" kann

(vgl. ).

So mit das Schlimmste in der Schulmathematik sind aber die fix & fertigen Lehrgänge, die sich besonders schön darin zeigen, dass man die gesamte Schulzeit an einem Schulbuch (oder genauer: einer Serie von Schulbüchern) entlang hangelt:

usw. usf. bis

(oder man nehme ein moderneres Schulbuch)

Da kann man nur sagen: , öffnet die Lehrgänge!

Die fatale "Fertigkeit" zeigt sich aber beispielsweise auch am zentralen mathematischen Thema der "Funktionen":

1. entwickeln SchülerInnen fast nie selbst Funktionen (s.u. 5.), sondern dürfen nur vorgefertigte Funktionen in einer sogenannten "Kurvendiskussion" "diskutieren"

(das kommt mir vor wie "katholische Demokratie": "die da unten" dürfen ja zu dem sagen, was "die da oben" längst beschlossen haben; was für ein Hohn!).

2. sind auch die Funktionsgraphen immer schon fertig: z.B. impliziert die quadratische Funktionsgleichung f: y = x² automatisch als fertigen Graphen die Parabel 

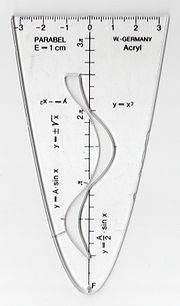
(die man sogar fertig kaufen kann).

Aber seien wir genauer und wohl auch fairer:

• anfangs wird diese Parabel im Unterricht ja üblicherweise sehr wohl aus einer Wertetabelle hergeleitet;
• auf die Dauer ist es natürlich praktisch, den Graphen nicht immer neu entwerfen zu müssen, sondern einfach zu wissen, dass beispielsweise der Graph zur Funktion g: y = -3x²-7x+5 auch parabelförmig ist.

Aber selbst wenn ein Graph aus einer Wertetabelle hervorgeht, entsteht er im üblichen Unterricht eben doch nie sukzessive durch Bewegung: die Zukunft ist immer fix & fertig bzw. sicher (es wird eine Parabel werden!), statt dass sie dramatisch (mit aller Unsicherheit) nacheinander "erwandert" wird:

Und so signalisiert ein Wendepunkt dann eben auch nie eine Enttäuschung oder Hoffnung, sondern er wird in einer üblichen "Kurvendiskussion" nur schnöde festgestellt

("... und in China ist ein Sack Reis umgefallen").

Da sei doch darauf hingewiesen, dass kein Geringerer als Newton, also sozusagen der Großmeister der Funktionen, sich Funktionen immer in Bewegung (d.h. auch sukzessiver Entstehung) vorgestellt hat und überhaupt erst dieser Ansatz ihn zur Entdeckung von Ableitung und Integral geführt hat.

Man wird merken: es geht mir hier wieder mal weniger um Anwendung als um Anschauung bzw. um tragfähige Vorstellungsmodelle.

Schade finde ich es nebenbei auch, dass im üblichen Schulunterricht die Steigung eines Funktionsgraphen immer nur berechnet statt auch mal mit einem

"Klinometer" bzw. "Neigungsmesser"

gemessen, Steigung also nie "getan" wird.

3. Weitgehend unüblich ist es in der Schulmathematik auch,

• statt aus der Funktionsgleichung den Graphen
• umgekehrt aus dem Graphen die Funktionsgleichung zu erschließen.

Also angenommen mal, wir kennen (ansatzweise) einen Funktionsgraphen, aber noch nicht die zugehörige Funktionsgleichung, was doch geradezu der Standard bei vielen Anwendungen ist: man hat eine Datenreihe, die (vielleicht abgesehen von einigen Ausreißern) eine bestimmte Funktion nahelegt, und versucht nun die Daten durch solch eine Funktion anzunähern.

Ein schöner Schritt weiter ist es da schon, dass in Schulen vermehrt die  (gar nicht so lineare) "lineare Regression" durchgenommen wird. 

Aber das Problem schreit doch auch nach anderen Verfahren wie beispielsweise Spline- bzw. Bezierkurven.

Nehmen wir doch als Beispiel mal einen

"Potentialtrichter".

Er ist so faszinierend, dass zumindest kleine Kinder andauernd ihre Eltern um Kleingeld anbetteln, das sie in solche Trichter hinein trudeln lassen können.

Vielleicht möchte man da ja auch mal wissen

(aber solche Neugierde auf die Funktionsweise ist anscheinend gar nicht selbstverständlich und wird schon gar nicht in den meisten Naturwissenschaftsmuseen erzeugt und befriedigt),

wie solch ein "Potentialtrichter" denn überhaupt funktioniert, d.h. welche Gestalt der Trichter haben muss, damit ein Geldstück schön kurvenreich und lange in seinen Schlund hinein rollt.

Klar ist immerhin, dass der Potentialtrichter (wie jeder Trichter!) von oben gesehen rund bzw. "rotationssymmetrisch" sein muss. Aber wie (genau!) muss er von der Seite aussehen, damit er richtig FUNKTIONiert?

Dazu denken wir uns erstmal

(und genau das ist bereits "richtige Mathematik!)

allen Schnickschnack (Geldzulauf oben, Geldauffangbehälter unten) weg und erhalten in vollendeter Ästhetik:

Da der Trichter symmetrisch ist, reicht zur Betrachtung eine (im folgenden die rechte) Hälfte und da die "Außenkante":

Unser abgenagtes Ergebnis ist also:

Aber das abgenagte Ergebnis allein hilft uns nicht weiter, denn schließlich wollen wir wissen, warum solch eine Kurve vorliegt - und dazu rüsten wir den Trichter eben doch wieder auf, und zwar mit dem Geldzulauf oben. Dieser gibt uns nämlich erst den entscheidenden Tipp, wie das Geldstück sich in dem Trichter bewegt und wie der Trichter deshalb aussehen muss:

Das Geldstück wird durch die Zulaufbahn so beschleunigt, dass es auf der Außenkante in den Trichter rollt, und es läuft nur kontinuierlich weiter, wenn es immer auf dieser Außenkante bleibt.

Mathematisch gesagt: es muss beim Runtertrudeln immer senkrecht auf der Kurventangente stehen:

Nun müssen wir uns aber überlegen, welche Kräfte auf das Geldstück wirken:

• einerseits befindet es sich in einer permanenten, nach außen gerichteten Rundbewegung,
• andererseits wird es durch die Schwerkraft nach unten in das Groschengrab gezogen

(wer da bereits an ein "Schwarzes Loch" denkt, sei noch kurz auf weiter unten vertröstet):

Und beide Kräfte zusammen sorgen dafür, dass das Geldstück permanent auf seiner Kante jongliert, und somit für sein spiralförmiges Runtertrudeln.

Anders gesagt: die Stellung des Geldstücks sollte sich an jedem Ort irgendwie (???) als Resultierende - - - (Vektoraddition) der beiden nach außen und unten wirkenden Kräfte ergeben!?

Damit haben wir schon allerlei über die Funktionsweise des Trichters erfahren, wissen aber immer noch nicht, welche Funktion da eigentlich vorliegt.

Ohne genauere Physik lässt sich da aber vermutlich auch nicht mehr erfahren, aber ich meine, dass ja auch schon die bisherigen (auch mathematischen!) Erkenntnisse allemal lohnen. Und überhaupt:

Allerdings könnte man dem bereits vorhandenen Funktionsgraphen auch einige markante Punkte entnehmen und diese durch ein Regressionsprogramm durchrechnen lassen, womit man

(MathematikerInnen mit einem "Auge" für die Eigenheiten verschiedener Funktionsgraphen mögen es längst vermutet haben)

nach

Umdrehen des Trichters bzw. des Funktionsgraphen

eine einfache Hyperbel, nämlich zur Funktion h: y = ¹ / _x, erhält:

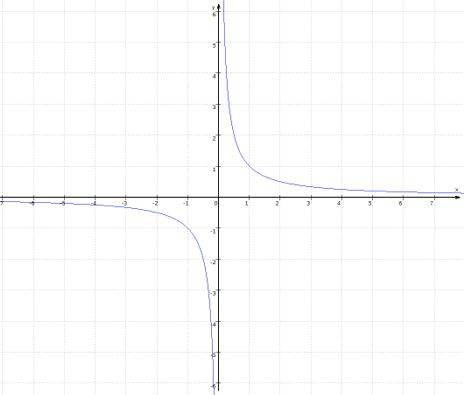
Und tatsächlich bestätigt der für die Herstellung des Trichters Verantwortliche:

Sehr geehrter Herr Stauff, 

bei diesem Potentialtrichter handelt es sich um ein "1/r-Potential", d.h. es handelt sich um die Fläche, die durch die Rotation einer Hyperbel entsteht. Darauf läuft die Münze gut. Auch bei anderen Potentialen, etwa dem 1/r^2-Potential, soll es gut funktionieren, das habe ich selbst aber noch nicht gesehen.

Mit den besten Grüßen,

Albrecht Beutelspacher 

-----
Prof. Albrecht Beutelspacher

Direktor

Mathematikum Gießen e.V.

Zum mathematischen und physikalischen Potential von Potentialtrichtern (und warum die überhaupt so heißen) vergleiche auch:  

Ansonsten vermute ich als physikalischer Laie aber so einige interessante Effekte:

1. den "Kreiseleffekt", d.h. die Selbststabilisierung durch schnelle Rotation,
2. , dass der "Trichter" immer enger, dadurch die Münze immer schneller und somit auch die Fliehkraft immer größer wird:

Vgl. ähnliche Beispiele in   und