oder
mathematischer
big bang
 und big crunch
und big crunch 
der Winkel zwischen zwei Vektoren
oder
mathematischer
big bang  und big crunch
und big crunch 
Da das, was ich hier zeigen möchte, allüberall in der Mathematik wichtig ist, ist das Beispiel, an dem ich es zeige, beliebig. Also sei die Berechnung des Winkels zwischen zwei Vektoren das Beispiel.
Dabei sei das Thema nicht "wie kommt man »drauf«?", und ebenso wenig sei darauf eingegangen, wozu man sowas "braucht". Des weiteren seien all die Vorarbeiten nicht erwähnt, die zur unten folgenden Rechnung nötig sind
(also z.B. die Herleitung des Skalarprodukts).
Sondern mich interessiert allein der Rechenweg, der zur Berechnung des Winkels zwischen zwei Vektoren hinführt:
big bang 
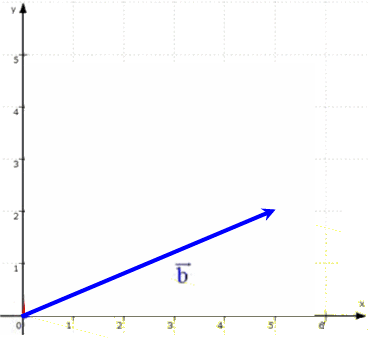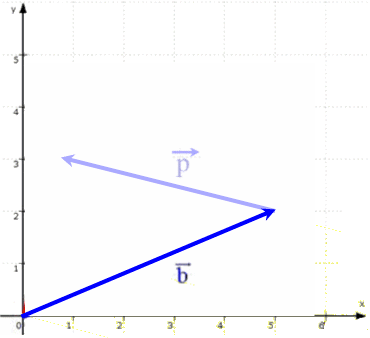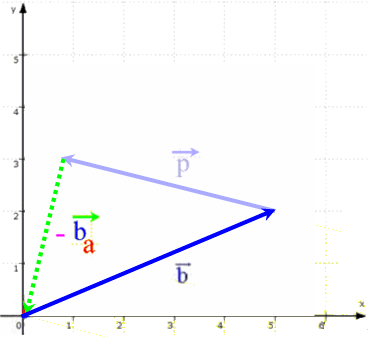
Gegeben seien die beiden Vektoren  und
und 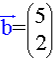 :
:
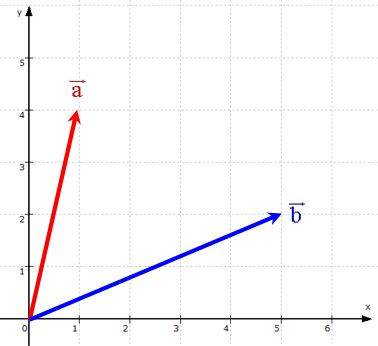
Da rechnen wir auf Vorrat erstmal einige Standardwerte aus:
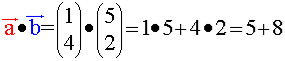 =
13 bzw. kurz
=
13 bzw. kurz ![]() •
•![]() = 13 ,
= 13 ,
also eine noch relativ einfache, weil kleine natürliche Zahl;
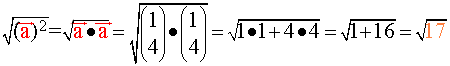 bzw. kurz
bzw. kurz a = ![]() ,
,
also eine doch schon ziemlich unangenehme (irrationale) Zahl;
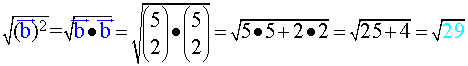 bzw. kurz
bzw. kurz b = ![]() ,
,
also wieder eine ziemlich unangenehme (irrationale) Zahl
(und nebenbei: für a und b ergeben sich die Wurzeln zweier verschiedener Primzahlen, was man als besonders unangenehm empfinden könnte;
vor allem aber: ![]() und
und ![]()
![]() , sondern als "richtige" MathematikerInnen vertrauen wir darauf, dass sich die Wurzeln irgendwann in der weiteren Rechnung von selbst "wegquadrieren" ).
, sondern als "richtige" MathematikerInnen vertrauen wir darauf, dass sich die Wurzeln irgendwann in der weiteren Rechnung von selbst "wegquadrieren" ).
Im nächsten Schritt betrachten wir den Projektionsvektor ![]() , der sich ergibt, wenn man
, der sich ergibt, wenn man ![]() senkrecht auf
senkrecht auf ![]() projiziert:
projiziert:
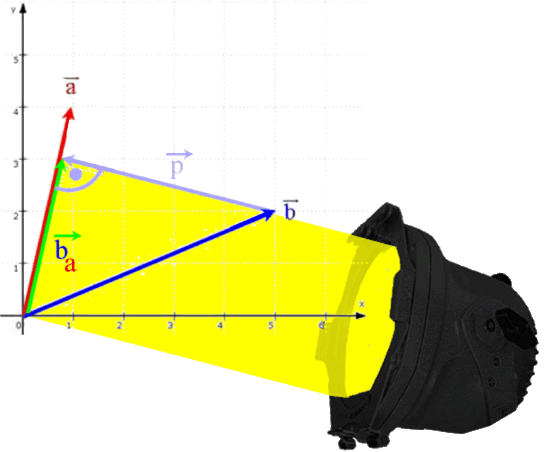
Wir wollen nun die Länge ![]() des Vektors
des Vektors ![]() bestimmen. Dazu benutzen wir zwei "Tricks":
bestimmen. Dazu benutzen wir zwei "Tricks":
 und somit auch zu
und somit auch zu 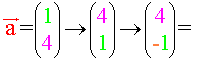
![]() .
.
Diesen Vektor ![]() zeichnen wir nun zusätzlich ein:
zeichnen wir nun zusätzlich ein:
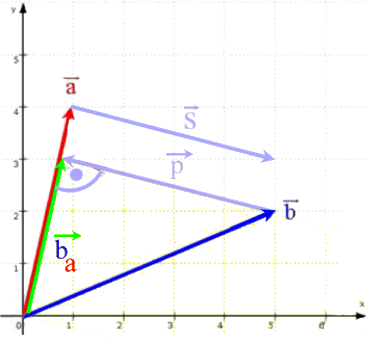
Hier gilt es kurz innezuhalten, um nicht auf allzu Suggestives hineinzufallen:
![]() = x •
= x • ![]()
(* wobei x negativ ist und sein Betrag ein bisschen größer als 1: es lohnt sich zur Kontrolle späterer Rechenergebnisse immer, vorher zu überlegen, was überhaupt rauskommen kann/muss);
![]() = y •
= y •
![]()
(** wobei y positiv ist und ein bisschen kleiner als 1).
 einen "Standardtrick" an, versuchen nämlich, einen "geschlossenen Vektorzug" zu finden, der (fast) alle wichtigen Vorgaben enthält. "geschlossen" heißt dabei, dass wir einmal im "Kreis" gehen bzw. mehrere Vektoren so aufaddieren, dass ihre Summe den Nullvektor
einen "Standardtrick" an, versuchen nämlich, einen "geschlossenen Vektorzug" zu finden, der (fast) alle wichtigen Vorgaben enthält. "geschlossen" heißt dabei, dass wir einmal im "Kreis" gehen bzw. mehrere Vektoren so aufaddieren, dass ihre Summe den Nullvektor
Auch hier lohnt es sich wieder, genau hinzuschauen:
"(fast) alle"
wichtigen Vorgaben enthalten sollte. "fast", weil wir vorerst
![]() nicht mit berücksichtigen;
nicht mit berücksichtigen;
insgesamt erhalten wir also
![]() =
= ![]() +
+ ![]() -
- ![]()
In diese Gleichung setzen wir nun alles Bekannte ein:
![]() =
= ![]() + x •
+ x • ![]() - y •
- y •
![]()
Halten wir kurz inne: somit ist der soeben noch vermisste Vektor
![]() nun doch wieder aufgetaucht, d.h. nun enthält unsere Gleichung tatsächlich alle relevanten Informationen.
nun doch wieder aufgetaucht, d.h. nun enthält unsere Gleichung tatsächlich alle relevanten Informationen.
Wenn wir nun auch für ![]() und
und
![]() konkrete Vektoren einsetzen, erhalten wir
konkrete Vektoren einsetzen, erhalten wir
![]() =
= ![]() + x •
+ x • ![]() - y •
- y • ![]() ,
,
und das ist äquivalent mit dem Gleichungssystem
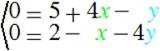 .
.
Wir sparen uns alle Zwischenschritte - und erhalten
x = ![]() , y =
, y = ![]() .
.
An diesen scheinbar wieder scheußlichen Ergebnissen ist Einiges bemerkenswert:
und in der Tat: wenn wir die Länge ![]() des Vektors
des Vektors ![]() berechnen und
berechnen und ![]() = y •
= y •
![]() gilt, so ist offensichtlich
gilt, so ist offensichtlich ![]() =
= ![]() •
a =
•
a = ![]() •
•
![]() =
= ![]() oder kurz
oder kurz ![]() =
= ![]() , d.h. wir erhalten (vorerst) ein noch scheußlicheres Ergebnis.
, d.h. wir erhalten (vorerst) ein noch scheußlicheres Ergebnis.
big crunch  zum Ersten
zum Ersten
"Der Big Crunch  bezeichnet ein mögliches zeitliches Ende des Universums als Gegenstück zum Urknall, wobei das Universum immer kleiner wird bis es schließlich ganz verschwindet." bezeichnet ein mögliches zeitliches Ende des Universums als Gegenstück zum Urknall, wobei das Universum immer kleiner wird bis es schließlich ganz verschwindet."(Quelle: |
Nun rechnen wir spaßeshalber a • ![]() =
= ![]() •
•
![]() = 13 oder kurz a •
= 13 oder kurz a • ![]() = 13 .
= 13 .
Daran ist nun wieder zweierlei bemerkenswert:
|
|
Nach einer gigantischen Rechnung (big bang) rauscht also urplötzlich alles in einem big crunch auf eine ganz simple Gleichung zusammen.
Und etwa so, wie man von einem zu Beginn des big bang sehr schnellen, "inflationären" Wachstum redet, könnte man hier von einem "inflationären", d.h. rasend schnellen big crunch reden.
Genau das aber ist für weite Teile der Mathematik weit über das vorliegende Beispiel hinaus typisch: dass sich nach gigantischen Rechen-Vorarbeiten (big bang) urplötzlich ein ganz simples Ergebnis einstellt (big crunch).
Schauen wir uns aber ![]() •
•![]() = a •
= a •
![]() nochmal genauer an:
nochmal genauer an:
das bedeutet insbesondere:
es ist also mal wieder, als wenn ein und derselbe Zusammenhang in zwei unterschiedlichen Sprachen ausgedrückt wird
(vgl.  )
)
Bzw. um im astronomischen Bildbereich zu bleiben, sprechen wir von einem
Wurmloch 
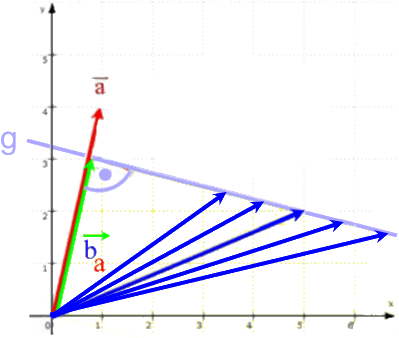
In unserem Fall springen wir also nach Lust und Laune von der Vektor- in die Elementargeometrie und zurück:
Um nun endlich den Winkel
Hier wollen wir den zweiten, also trigonometrischen Zugang nutzen - und springen somit aus der Vektor- in die Elementargeometrie, was auch heißt: aus der vektorgeometrischen Zeichnung
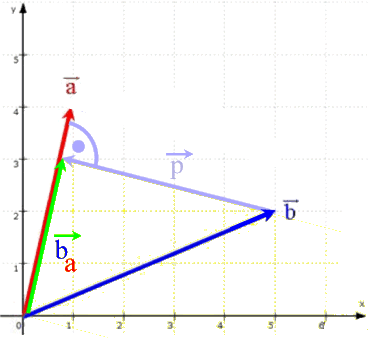
wird durch simples Weglassen aller Vektor-Pfeilspitzen die elementargeometrische Zeichnung
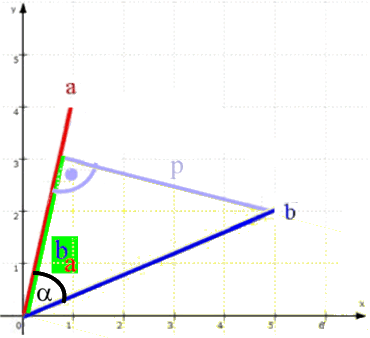
In dem rechtwinkligen (!) Dreieck gilt nun
![]()
oder kurz
![]()
und wenn man das nach ![]() auflöst, ergibt sich
auflöst, ergibt sich
![]() .
.
Dieses wiederum eingesetzt in
![]() •
•![]() = a •
= a •
![]()
ergibt
| |
und somit nach wiederum langer Rechnung (big bang) ein schnuckelig kurzes Ergebnis, also
big crunch  zum Zweiten
zum Zweiten
Weil wir nun aber in der Gleichung
![]() •
•![]() = a •
= a •
![]()
allesamt bereits kennen, ergibt sich
13 = ![]() •
•
![]() •
cos(
•
cos(![]() ) .
) .
cos(![]() ) =
) = ![]()
Hier quadrieren sich die Wurzeln nun nicht mehr raus
(und dennoch lohnt es sich, die Wurzel-Kurzschreibweise bis hier mitzuschleppen, statt andauernd mit dezimalen Näherungswerten und somit vielleicht immer schlimmer werdenden Fehlern zu rechnen),
und deshalb bemühen wir erstmals einen Näherungswert, nämlich
cos(![]() ) ≈ 0,5854
) ≈ 0,5854
Und daraus ergibt sich als Winkel zwischen den beiden Vektoren ![]() und
und ![]()
![]() ≈ 540
≈ 540

"Was lernen wir draus [= aus alledem]?":