die bildschöne Zahl 3-5
Und schon - so vermute ich mal - werden sich die Geister scheiden: wie kann man denn etwas so Abstraktes wie Zahlen schön finden?
Immerhin gibt es verschiedene Ebenen des (möglichen) Schönfindens:
-
eine Zahl sieht optisch schön aus, was man wegen der Symmetrie z.B. bei 8 meinen mag.
-
mag man auch
(und damit deutet sich schon das eigentliche Thema dieses Aufsatzes an; s.u.)
Muster schön finden, die sich aus der Kombination mehrerer Ziffern ergeben, also beispielsweise
-
69 (:-)
-
666 (also die berühmte Zahl aus der Apokalypse)
-
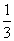 = 0,3333333333333333333333333333333333333333333333...
= 0,3333333333333333333333333333333333333333333333...
-
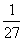 = 0,037 037 037 037 037 037 037 037 037 037 037...
= 0,037 037 037 037 037 037 037 037 037 037 037...
-
man mag einfache Zahlen als schön empfinden
(also z.B. die natürlichen Zahlen 1, 2, 3, 4, 5, 6, 7, 8, 9),
wie ja überhaupt in der Mathematik
(aus anderen Leuten unverständlicher Mathematikersicht)
oftmals gilt:
Einfachheit = Schönheit.
-
Man mag also auch Zahlen schön finden, die zwar nicht "an sich", aber doch "in Funktion" einfach sind, d.h. mit denen sich einfach rechnen lässt.
(beispielsweise ist das Rechnen mit 10 besonders einfach, weil man etwa bei der Multiplikation mit 10 an die Ausgangszahl nur eine 0 anhängen muss).
-
MathematikerInnen finden zudem noch Zahlen schön, die im Gesamtzahlenraum raffiniert verteilt sind, also beispielsweise Primzahlen:
-
es gibt bewiesenermaßen unendlich viele davon,
-
sie bilden auch vielfach Muster, nämlich z.B. Primzahlzwillinge
(also direkt benachbarte Primzahlen wie z.B. 11 und 13, zwischen denen nur eine gerade Zahl, nämlich hier 12, liegt;
von den Primzahlzwillingen ist aber noch nicht klar ist, ob es unendlich viele davon gibt),
Bei 3-5 ist aber (zumindest auf der ersten Blick) keines der soeben angeführten Schönheitskriterien erfüllt, ja mehr noch:
vielen Leuten wird es vermutlich sogar so erscheinen, dass da gar nicht eine Zahl vorliegt, sondern die Kombination aus den zwei Zahlen 3 und -5.
Nun ist es aber in der Mathematik irritierenderweise oftmals so, dass es
-
verschiedene, häufig sogar sehr unterschiedlich aussehende Schreibweisen
-
für ein und dieselbe Zahl gibt
(mal ist die eine, mal die andere Schreibweise nützlich).
In unserem Beispiel gibt es mindestens vier solche Schreibweisen:
3-5 = 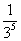 =
= 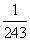 ≈ 0,00411522633744855
≈ 0,00411522633744855
(vgl. zur Herleitung  )
)
Vor der letzten, also der Dezimalschreibweise, wurde vorsichtshalber ein Ungefähr-Zeichen gesetzt, weil Computer ja notorisch zu Rundungsfehlern neigen.
(es gibt auch exaktere Begründungen für das Setzen des Ungefährzeichens: siehe die Überlegungen ganz am Ende dieses Aufsatzes).
Die Rechnung 3-5 = 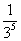 =
= 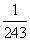 ≈ 0,00411522633744855 ergab sich eher zufällig im Aufsatz
≈ 0,00411522633744855 ergab sich eher zufällig im Aufsatz  , und das auch nur, weil ich irgendwelche Potenzen dividieren wollte und da (fast) zufällig 39 und 34 gewählt hatte.
, und das auch nur, weil ich irgendwelche Potenzen dividieren wollte und da (fast) zufällig 39 und 34 gewählt hatte.
Nun rechne ich ja normalerweise 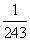 nicht aus, d.h. der passende Dezimalwert ist mir meistens herzhaft egal
nicht aus, d.h. der passende Dezimalwert ist mir meistens herzhaft egal
(vgl.  ).
).
Als ich es dann aber doch mal mittels Taschenrechner tat, ergab sich eben
0,00411522633744855,
und das ist einerseits im Vergleich mit den anderen Schreibweisen 3-5 , 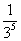 und
und 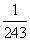 ganz schön scheußlich
ganz schön scheußlich
(ich werde nie verstehen, weshalb so viele SchülerInnen versessen auf Taschenrechnerergebnisse, also Dezimalzahlen sind)
- und andererseits doch bildschön!
Vielleicht sieht man ja schon, dass die Zahl 0,00411522633744855 halbwegs in das o.g. zweite Schönheitskriterium passt, also ein interessantes Muster hat.
Allerdings steht da kein sich ewig langweilig wiederholendes, unverändertes Muster
(wie z.B. bei 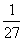 = 0,037 037 037 037 037 037 037 037 037 037 037 ...)
= 0,037 037 037 037 037 037 037 037 037 037 037 ...)
sondern sozusagen ein sich entwickelndes "Meta-Muster":
0, 004 115 226 337 448 55
Wenn man dieses Muster erstmal erkannt hat, kann man es
( 00 → 11 → 22 → ...
4 → 5 → 6 → ...)
(vorerst) fortsetzen, nämlich als
0, 004 115 226 337 448 559 66
Solch ein Strickmuster aus
kommt mir aber aus einem anderen Zusammenhang schwer bekannt vor.
| Intermezzo: Die sogenannten "rationalen" (vernünftigen!) Zahlen sind sowohl -
als Bruch aus zwei ganzen Zahlen schreibbar (z.B. 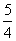 oder oder 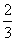 ) ) -
oder als Dezimalzahlen, die hinter dem Komma -
entweder endlich sind (z.B. 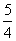 = 1,25) = 1,25) -
oder aber periodisch (z.B. 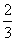 = 0,66666666666666666666666 ...) = 0,66666666666666666666666 ...) sind. Da kann man doch die Frage stellen, ob es auch sogenannte "ir-rationale" (also unvernünftige!) Zahlen gibt (geben kann), die also als in Dezimalschreibweise hinter dem Komma -
nicht endlich -
und nicht periodisch sind. Auf diese Frage gibt es zwei verschiedene Antworten: -
den Beweis, dass beispielsweise die 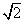 irrational ist. irrational ist. (vgl. 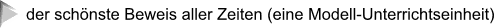 ) ) So schön dieser Beweis ist, so hat er doch den Nachteil, dass dabei die Dezimalschreibweise von 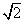 gar nicht vorkommt, man also auch nicht sieht, was in dieser Dezimalschreibweise hinter dem Komma passiert. Und der Näherungswert 1,414213 könnte ja immer noch gar nicht vorkommt, man also auch nicht sieht, was in dieser Dezimalschreibweise hinter dem Komma passiert. Und der Näherungswert 1,414213 könnte ja immer noch -
entweder hinter der 3 bereits abbrechen, also endlich hinter dem Komma sein, -
oder doch periodisch weiterführbar sein (z.B. 1,414213 414213 414213 ...). Der genannte Beweis hat also den typischen Nachteil eines sogenannten "Existenzbeweises", nämlich, dass man zwar weiß, dass es etwas gibt, aber nicht, wie es aussieht. (Aber nichts gegen reine Existenzbeweise, die doch -
sozusagen die Pioneer-Sonden der Mathematik -
und geradezu grandios katholisch sind: es gibt den Heiligen Geist, obwohl ihn noch nie jemand gesehen hat. Ein Beispiel: man kann beweisen, dass es beliebig große Lücken zwischen den schon oben genannten Primzahlen gibt, auch wenn man nicht weiß, wo sie liegen.) -
möchte man solch eine hinter dem Komma -
nicht endliche -
und nicht periodische Dezimalzahl ja vielleicht doch einmal sehen. Nun sollte man aber denken, dass das völlig ausgeschlossen ist, denn etwas Unendliches kann man garantiert niemals sehen. Nun ist der "gesunde Menschenverstand" bzw. die Mathematik ja doch ganz schön raffitückisch - und findet auf einem Umweg dennoch zum Ziel: wir bräuchten ziemlich schnell hinter dem Komma ein Muster, das wiederholt, denn in letzterem Fall läge ja doch wieder eine Periode vor. Ein Weg, das Problem zu lösen, wurde oben schon nebenher angedeutet: entwickelt man eine Zahl. Beispiel A: Es ergibt sich: 0, 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 19 19 20 21 ... Und diese Dezimalzahl ist offensichtlich (?) also irrational! Beispiel B: Es ergibt sich: 0, 10 100 1000 10000 100000 1000000 ... Auch diese Dezimalzahl ist offensichtlich (?) also irrational! (Und nach dem Vorbild dieser beiden Beispiele A und B kann man natürlich unendlich viele andere irrationale Zahlen konstruieren.) Die beiden Beispiele A und B wirken auf mich aber arg konstruiert. |
| Hingegen scheint sich bei 3-5 = 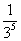 = = 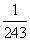 ≈ 0, 004 115 226 337 448 55 ≈ 0, 004 115 226 337 448 55 solch eine irrationale Zahl regelrecht "von selbst" (bzw. durch die Rechnungen 3-5 = 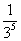 = = 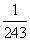 ) ) zu ergeben. "Schön" an 3-5 = 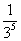 = = 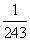 ist also höchstens, dass da Rechenanweisungen stehen, die die schöne Zahl 0, 004 115 226 337 448 55 ergeben. ist also höchstens, dass da Rechenanweisungen stehen, die die schöne Zahl 0, 004 115 226 337 448 55 ergeben. Und da könnte man doch immerhin vermuten, dass es ähnliche Rechenanweisungen gibt, die systematisch zu anderen wohlsortierten und doch irrationalen Zahlen führen. |
Oben war schon gezeigt worden, wie die Zahl
0, 004 115 226 337 448 55
nach der sich andeutenden Regel weitergestrickt werden kann, nämlich
0, 004 115 226 337 448 559 66.
Mit der bei Beispiel A und B angewandten Ziffernschreibweise von Zahlen kann man das auch noch über die 9 bzw. 99 hinaus, also bis in alle Ewigkeit fortsetzen:
0, 004 115 226 337 448 559 6610 7711 8812 9913 101014...
Die so konstruierte Zahl ist wieder hinter dem Komma
-
nicht endlich
-
und nicht periodisch,
also irrational!
| Nur leider, leider geht 3-5 = 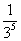 = = 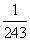 in Wirklichkeit in Wirklichkeit (wenn man mehr Nachkommastellen berücksichtigt, also beispielsweise einen leistungsfähigeren Taschenrechner benutzt) nicht mehr so hübsch systematisch weiter, sondern verliert irgendwann diese Systematik: 3-5 = 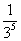 = = 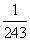 ≈ 0, 004 115 226 337 448 559 670781893 ≈ 0, 004 115 226 337 448 559 670781893 |
Wenn man aber einen noch besseren Taschenrechner benutzt, fällt einem vielleicht auf:
3-5 = 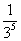 =
= 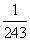 ≈ 0, 004 115 226 337 448 559 670781893 004 115 22,
≈ 0, 004 115 226 337 448 559 670781893 004 115 22,
dass ganz weit hinten also derselbe Rattenschwanz wieder loszulegen scheint wie anfangs, sich also eben doch wieder Periodizität anzudeuten scheint.
Nun, ganz so überraschend ist das ja nicht:
| 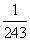 ist als Bruch eine rationale Zahl, d.h. die entsprechende Dezimalschreibweise muss hinter dem Komma ist als Bruch eine rationale Zahl, d.h. die entsprechende Dezimalschreibweise muss hinter dem Komma
-
entweder endlich -
oder aber periodisch sein. Mehr noch: da nur durch Dreierpotenzen dividiert wird, ist von Anfang an klar, dass die Dezimaldarstellung früher oder später nichtendlich-periodisch werden muss. |
Interessant finde ich auch die (hier unbeantwortete) Frage, wie
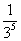 =
= 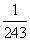 = 0,004115226337448559670781893
= 0,004115226337448559670781893
durch mehrfache Multiplikation von Dritteln miteinander zustande kommt:
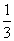 = 0,333333333333333333333333333333333... = 0,3
= 0,333333333333333333333333333333333... = 0,3
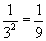 = 0,111111111111111111111111111111111... = 0,1
= 0,111111111111111111111111111111111... = 0,1
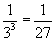 = 0,037037037037037037037037037037037... = 0,037
= 0,037037037037037037037037037037037... = 0,037
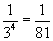 = 0,012345679012345679012345679012346... = 0,012345679
= 0,012345679012345679012345679012346... = 0,012345679
... wobei das letzte Ergebnis seinerseits wieder hochinteressant ist, ergeben sich da doch nacheinander die Ziffern 0 bis 9, allerdings merkwürdigerweise mit Ausnahme der 8.
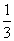 = 0,3333333333333333333333333333333333333333333333...
= 0,3333333333333333333333333333333333333333333333...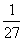 = 0,037 037 037 037 037 037 037 037 037 037 037...
= 0,037 037 037 037 037 037 037 037 037 037 037...