:
"Blechspielzeug" und Mathematik

Vgl. auch

"Wenn Eltern und Kinder eine Wäscheklammer anschauen
und sich fragen, was sie eigentlich dazu bringt,
immer wieder zuzuschnappen,
dann stehen sie schnell vor den großen ungelösten Fragen des Universums."
(Donata [!] Elschenbroich)

Das steht hier drüber, weil das Folgende mir

(zwischen all meinen sonstigen Aufsätzen)

besonders wichtig ist.

Oftmals schreibe ich einen Aufsatz und merke erst hinterher, dass ein Autor das, was ich zu sagen habe, schon vorher gesagt hat.

Oder ich finde lange nach dem Schreiben eine Quelle, die später Dasselbe oder Ähnliches gesagt hat.

Beides soll mir recht sein, unterstreicht es doch "nur" das, was ich sagen möchte. Und in beiden Fällen ergänze ich dann später Quellenverweise.

Im vorliegenden Fall ist es allerdings anders gelaufen: ich wollte schon lange einen Aufsatz zum hier vorliegenden Thema schreiben, als eigentlicher Anlass wirkte aber erst, dass ich in einer Buchhandlung in Boston das Buch

gefunden habe.

Zum Inhalt:

"»This is a book about science, technology, and love,« writes Sherry Turkle. In it, we learn how a love for science can start with a love for an object - a microscope, a modem, a mud pie, a pair of dice, a fishing rod. Objects fire imagination and set young people on a path to a career in science. In this collection, distinguished scientists, engineers, and designers as well as twenty-five years of MIT students describe how objects encountered in childhood became part of the fabric of their scientific selves. In two major essays that frame the collection, Turkle tells a story of inspiration and connection through objects that is often neglected in standard science education and in our preoccupation with the virtual.
The senior scientists' essays trace the arc of a life: the gears of a toy car introduce the chain of cause and effect to artificial intelligence pioneer Seymour Papert; microscopes disclose the mystery of how things work to MIT President and neuroanatomist Susan Hockfield; architect Moshe Safdie describes how his boyhood fascination with steps, terraces, and the wax hexagons of beehives lead him to a life immersed in the complexities of design. The student essays tell stories that echo these narratives: plastic eggs in an Easter basket reveal the power of centripetal force; experiments with baking illuminate the geology of planets; Lego® bricks model worlds, carefully engineered and colonized.
All of these voices - students and mentors - testify to the power of objects to awaken and inform young scientific minds. This is a truth that is simple, intuitive, and easily overlooked."
(Quelle: )

Es sind also oftmals technische Gegenstände und Spielzeuge, die jemanden langfristig zur (Natur-)Wissenschaft verführen. Obwohl nun aber in dem Buch die Mathematik nicht erwähnt wird, scheint mir Dasselbe auch für diese zu gelten: in vielen Biografien berühmter Mathematiker wird deutlich, dass es eben auch bei ihnen die frühe Faszination durch "objects" gegeben hat:

"Als Albert Einstein ein alter Mann war und sich daranmachte, einen kurzen Band mit autobiografischen Notizen zu verfassen - «so etwas wie den eigenen Nekrolog» -, erinnerte er sich an den Tag, an dem sein Vater ihm einen Kompass gezeigt hatte. Er hatte ihn hin und her gedreht und gestaunt, dass die Nadel dabei doch unablässig nach Norden zeigte. «Ich erinnere mich noch jetzt - oder glaube mich zu erinnern -, daß dieses Experiment tiefen und bleibenden Eindruck auf mich gemacht hat», schrieb Einstein. «Da mußte etwas hinter den Dingen sein, das tief verborgen war.»"

Im Hinblick auf die Mathematik unterscheide ich drei Arten "technischer Gegenstände":

1. Modelle, die überhaupt nur dazu geschaffen wurden, (inner-)mathematische Tatsachen und Vorgänge zu veranschaulichen

(vgl.   );

2. (auf den ersten Blick "unmathematisches") "konstruktives Spielzeug" wie z.B.

• Lego®

(vgl. auch die Buchbesprechung oben sowie ),

• Fischer-Technik ,
  
• Geomag ,
  
•   
  
  (Das Zometool-System wird weltweit von vielen Wissenschaftlern, Architekten, Künstlern und auch Nobelpreisträgern verwendet - namentlich Linus Pauling, Sir Rodger Penrose und Richard Smalley [der die Bucky Balls entdeckte]. Auch die brauch[t]en Veranschaulichung und Modelle, sogar die waren bzw. sind sich nicht dazu zu schade.)
  
• der klassische Metallbaukasten  :

Dieses Spielzeug schult die konstruktiven Fähigkeiten und das räumliche Vorstellungsvermögen, die man - so behaupte ich - eben auch in der Mathematik gut brauchen kann.

3. massenhaft alltägliche Gegenstände, die weder zur mathematischen Veranschaulichung noch als Konstruktionsspielzeuge gedacht sind.

Das schönste und gängigste Beispiel sind da Küchenutensilien, die für kleine Kinder jedes teure Spielzeug problemlos ersetzen und übertreffen:

(eine Snare-Drum)

• die "source domain" sind alltägliche Gegenstände,
• die "target domain" ist die Mathematik;
• die "source domain" besteht aus "image schemas"

(sowie Bewegungen und Tätigkeiten)

(anhand der Analogie zwischen einem Gegenstand und einem mathematischen Thema)

Insbesondere geht's mir auch darum, wieder eine Beziehung zwischen den alltäglichen Gegenständen und der Mathematik herzustellen:

• nicht in Form von Anwendungen der Mathematik auf die außermathematische Welt (die Gegenstände)
• sondern umgekehrt, indem die  Außenwelt (die Gegenstände) zum Verständnis der Mathematik nutzbar gemacht wird (werden):

vgl. "Anschauung statt Anwendung"

Es geht also sozusagen um die Wiedereinführung der Pfeifen in die Mathematik statt  .

Man kann den Blick für solche mathematisch nutzbaren "Pfeifen" trainieren - und sieht dann (wie ich) allüberall nur noch "Pfeifen":

"Wenn man ein Hammer ist, scheint einem die ganze Welt nur noch aus Nägeln zu bestehen",

d.h. der obsessive Blick auf mathematisch nutzbare Gegenstände hat natürlich etwas Wahnhaftes: der "normale", geistig gesunde Mensch darf die Welt nicht immer nur mit einem Raster messen, und er würde (fast wie ein Autist) überflutet, wenn er über alles und jedes staunen würde.

Aber es müsste doch möglich (und erlaubt) sein, den Blick von SchülerInnen für mathematisch verwertbare Alltagsgegenstände ein wenig zu schulen, und zwar einfach, indem man diese Gegenstände mit in die Schule bringt und die SchülerInnen sich an die mathematische Verwertung von Alltagsgegenständen gewöhnen.

Nun könnte ich hier in der Tat ein Riesenreservoire von mathematisch geeigneten Alltagsgegenständen aus meiner Sammlung vorstellen, aber ich bin (wieder) zu faul, sie alle zu fotografieren, die Fotos hier einzustellen und dann auch noch den jeweiligen mathematischen Aspekt zu besprechen.

Deshalb bleibe ich vorerst bei bereits erwähnten bzw. gezeigten Gegenständen:

• Magrittes "Pfeife": es ist schon lustig, dass ausgerechnet die Pfeife, die laut Bildunterschrift keine ist

(sondern eben nur ein Bild von einer Pfeife),

geradezu zum Inbegriff der Pfeife geworden ist: man suche nur mal in Google nach Bildern (!) zu den Begriffen "Pfeife" oder "pipe" - und erhält umgehend und mehrfach Magrittes Bild. 

Bemerkenswert finde ich aber auch, dass Magritte nicht irgendeine Pfeife gemalt hat, sondern eine, die etwa folgendermaßen aussieht:

 ,

also eine besonders schön geschwungene, also - mathematisch gesagt: - stetige, differenzierbare, fast schon sinusförmige Pfeife:

• Der "Schneebesen" ist
  • nicht nur eine dreidimensionale Funktionenschar,
  • sondern auch ein (wieder dreidimensionaler) Rotationskörper, bei dem die Einzeldrähte einige gut sichtbare Zwischenzustände sind.

Allerdings wird ein Schneebesen ja üblicherweise durch die Koch- bzw. Backzutat gezogen, aber nicht gedreht. Ein günstigeres Bild sind da die tatsächlich rotierenden "Quirlstäbe" (?) von Mixern:

• An einem

"Fächerspalier"

lassen sich gut die Strahlensätze zeigen und merken.

Allerdings hat auch diese "conceptual" zwei Nachteile:

1. enden die "Strahlen" nicht in einem Punkt

(bzw. gehen nicht von diesem aus),

sondern da müsste man nacharbeiten:

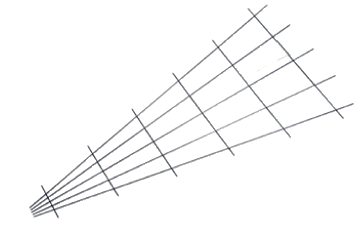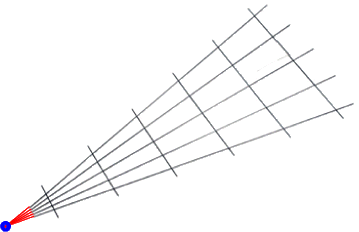
2. kann das zur Gesamtwinkelhalbierenden achsesymmetrische Fächerspalier

zu dem Irrtum verleiten, die Strahlensätze gälten nur bei solcher Achsensymmetrie. Lieber wäre mir da doch ein bewegliches Modell der folgenden Art:

 ,

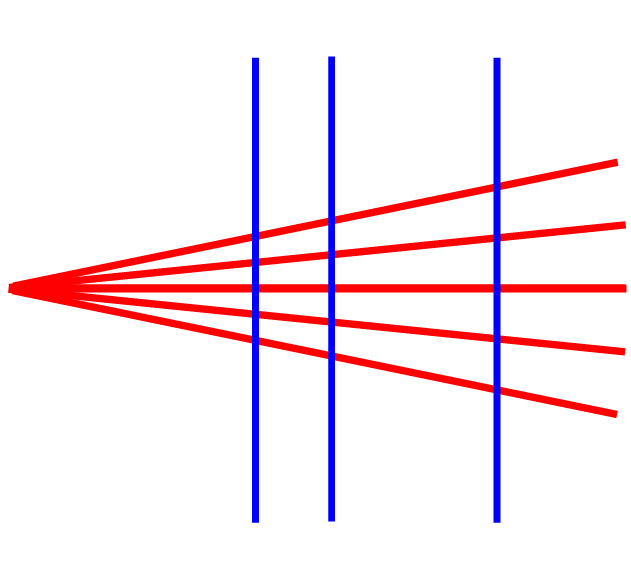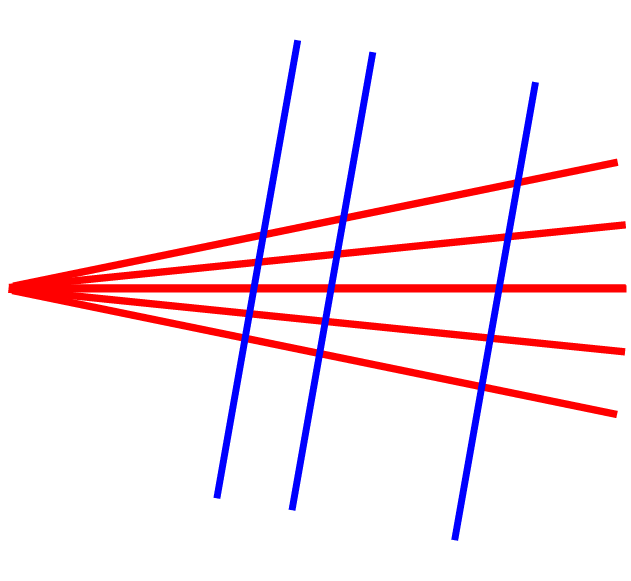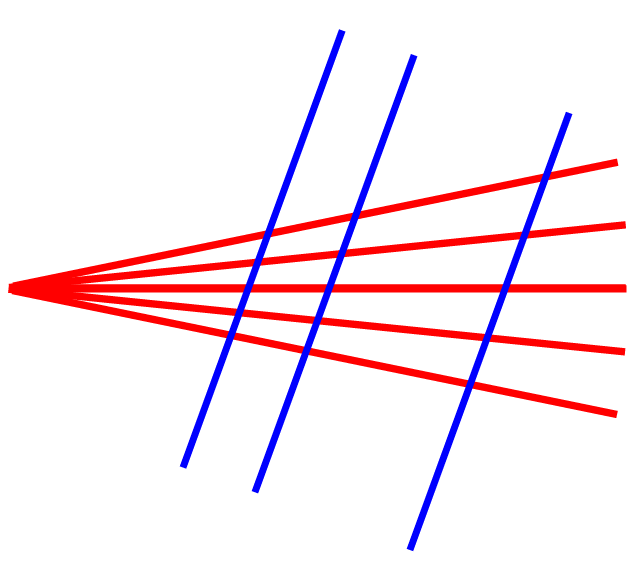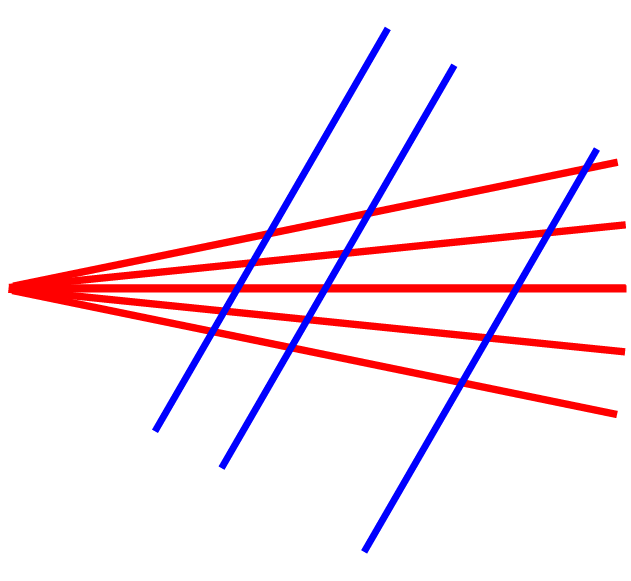Aber dafür gibt es meines Wissens im Alltag kein Beispiel - wenn auch derart interessante optische Effekte zustande kommen:

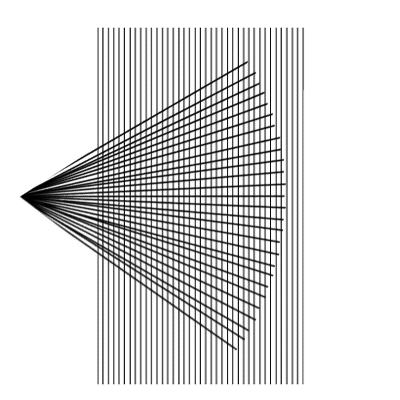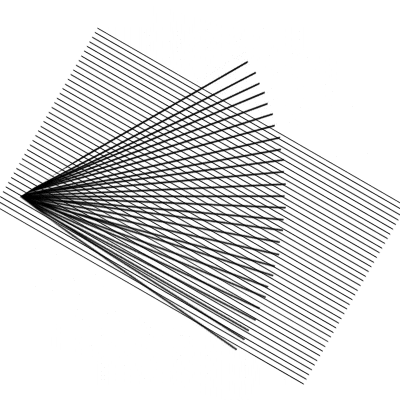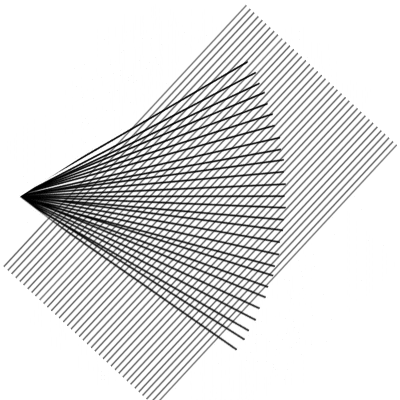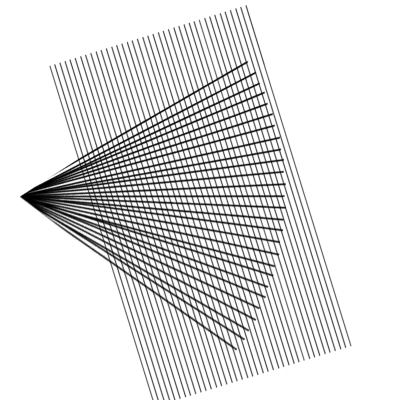
Als kleines Schmankerl

(wo oben schon von Rotationskörpern die Rede war)

seien auch noch dreidimensionale Varianten des Fächerspaliers gezeigt, bei denen es doch ebenfalls reizvoll wäre, nach den Strahlensätzen zu fragen:

(eigene Modellideen meines siebenjährige Sohnes)

• eine Lampe mit "Potentialtrichter" oben:

• und noch'n Potentialtrichter bzw. (annähernd) Hyperboloid:

Und dann gibt es noch - also viertens - das, was ich "pseudomathematische" Modelle nenne, d.h. Gegenstände, die vermutlich nichts (direkt) Mathematisches illustrieren und doch von der "Denkungsart" (???) her mathematisch sind.

Zwei Beispiele:

... woran mich weniger die Kombinatorik des Zusammensetzens interessiert als die geometrische Form und Konstruktion.

Und doch: als ich gesehen habe, wie schnell ein unvorbereiteter Schüler

zu

zusammengesetzt hat, habe ich mir sofort gedacht, dass er auch ein guter Mathematiker sein müsste.

Würd' mich nicht wundern, wenn ich irgendwann auch noch herausfände, welchen mathematischen Sachverhalt die so wundersam geschwungene Praline aus besonders gut darstellt.

(Fast allzu) selbstverständlich ist eine "reine" Mathematik vorstellbar, die keinerlei Bezug zu anderen (insbesondere Natur-)Wissenschaften hat. Wenn's hoch kommt, sind diese anderen Wissenschaften hübsche (oder auch gefährliche) Anwendungen bzw. Abfallprodukte der reinen Mathematik.

Naturwissenschaftler (und insbesondere Physiker) halten oftmals umgekehrt die Mathematik für eine schnöde Hilfswissenschaft.

Immerhin lässt sich sagen: die Mathematik kann (scheinbar) problemlos ohne alle Naturwissenschaft leben, aber eine Naturwissenschaft ohne Mathematik ist heutzutage schlichtweg undenkbar.

Genau dem aber widerspricht Mark Levi in seinem Buch: nicht nur, dass viele mathematische Entdeckungen erst aufgrund technischer oder naturwissenschaftlicher Erfordernisse stattgefunden haben, sondern die Physik (Mechanik) kann auch gute Vorlagen für mathematische Problemlösungen geben.