(Sogenannte "Funktionsplotter", also Computerprogramme, in die man Funktionsgleichungen eingeben kann und die dann die zugehörigen Graphen zeichnen, scheinen mir da nur die zweitbeste Lösung
[mangels anfassbarer Funktionsgraphen]
zu sein
- womit ja nicht die spezifischen Stärken dieser "Funktionsplotter" geleugnet seien:
schnelles Zeichnen,
Variation von Funktionsgleichungen und -graphen,
...)
Am besten geeignet wären wohl biegbare Leisten, aber woher nehmen?
Also bin ich auf die Idee gekommen, die Brio-Bahn meines Sohnes mit in den Unterricht zu nehmen und von den SchülerInneN verschiedenste Bahnen bauen zu lassen.
Hier zwei Ergebnisse:


Man wird vielleicht als Nachteil bemerken, dass die Koordinatenachsen nicht
senkrecht zueinander stehen, was natürlich daran liegt, dass ich die Brio-Bahnen nicht von oben, sondern schräg von der Seite fotografiert habe: die Bodenfliesen des Klassenraums zeigen, dass die Koordinatenachsen an ihnen ausgerichtet war.
Und schon haben wir etwas ganz Entscheidendes: die Gegebenheiten des Klassenraums werden nicht ignoriert (weg-abstrahiert), sondern ausdrücklich einbezogen: der Kunststoff-Fliesenboden ist ja bereits ein Koordinatensystem ("die Welt ist voller Koordinatensysteme").
Gleiches gilt für die Briobahn selbst: sie ist nicht schaler Ersatz für bessere Möglichkeiten
(s.o. biegbare Leisten),
sondern ihre speziellen konstruktiven Eigenarten (und auch Beschränkungen) werden nutzbar gemacht:
-
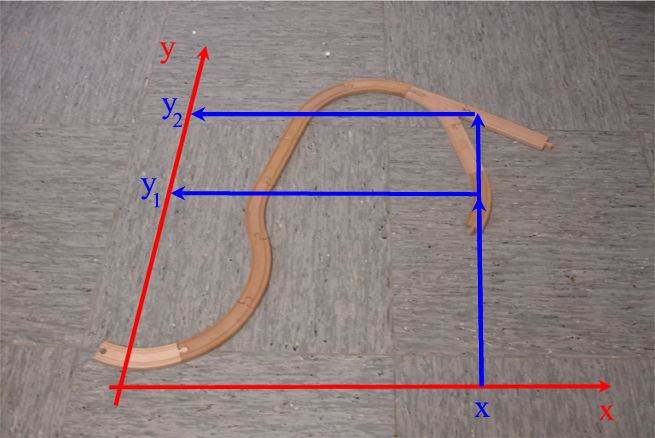
Beispielsweise liegt im zweiten Bild aus mehreren Gründen kein Funktionsgraph vor.
Einer der Gründe ist, dass bei (Brio-)Eisenbahnen Weichen möglich sind, die dafür sorgen, dass (mindestens) einem x mehrere y-Werte (hier y1 und y2) zugeordnet werden:
Merke: Funktionsgraphen dürfen keine Weichen haben.
(Nebenbei: ich hatte mit den SchülerInnen schon vorher einige Faustregeln dafür erarbeitet, was bei Funktionsgraphen nicht passieren darf:
sie dürfen nicht parallel zur y-Achse werden [vgl. c.],
sie dürfen nicht rückläufig sein [vgl. d.].
Aber auf das Verbot von Weichen war ich vorher, also ohne die Brio-Bahn, gar nicht gekommen.)
-
Die bei Kurvendiskussionen zentral wichtigen Wendepunkte sind bei Brio-Bahnen wegen des "Steck-Prinzips" nicht abstrakt, sondern regelrecht "fassbar", nämlich genau an den Verbindungspunkten
 :
:

-
Wie schon gesagt: Funktionsgraphen dürfen nicht parallel zur y-Achse sein, da auch dann wieder einem (einzigen) x mehrere y-Werte (sogar - wenn auch auf einem relativ kurzen Graphenstück - unendlich viele!) zugeordnet werden (hier nur gezeigt, für y1, y2 und y3, aber genauso alle y-Werte zwischen y1 und y3):
Wenn man nun aber in
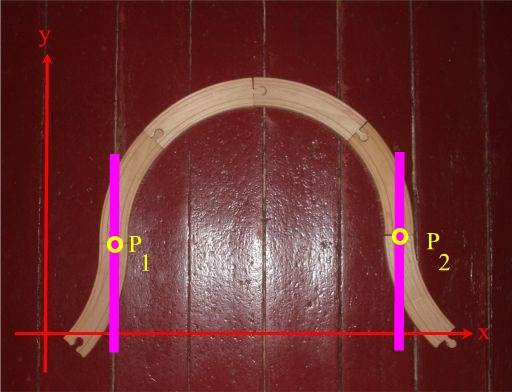
genauer hinschaut, entdeckt man da Folgendes:
Da hat der Graph in den Punkten P 1 und P2 Tangenten, die parallel (!) zu der y-Achse sind
(nebenbei: auch hier ist der konkrete Fußboden - diesmal in meinem Arbeitszimmer - eine gute Hilfe, bilden die Ritzen zwischen den Dielen doch fast genau die Tangenten in P 1 und P 2).
Oder weniger abstrakt gesagt: in P 1 und P2 ist die Brio-Bahn kurzfristig senkrecht (zur x-Achse) bzw. parallel zur y-Achse.
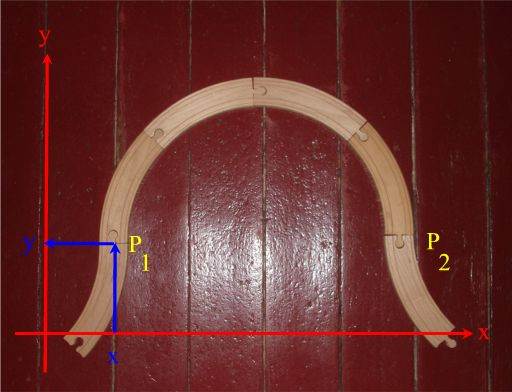
Trotzdem liegt ein Funktionsgraph vor, denn beispielsweise in P1 wird tatsächlich dem entsprechenden x nur ein y zugeordnet:
Natürlich liegt das daran, dass der Graph nicht "längerfristig" senkrecht (zur x-Achse) bzw. parallel zur y-Achse wird, sondern nur in den Einzelpunkten P 1 und P2., d.h. in unendlich kurzen "Augenblicken"
(womit schon der Limes-Begriff angedeutet wird!).
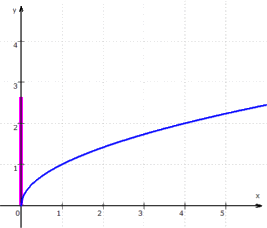
Die einzige "richtige" mathematische Funktion, die mir auf Anhieb einfällt und bei der einmal - und zwar im Ursprung - auch eine senkrechte Tangente vorliegt (aber dennoch auch eine Funktion), ist die Wurzelfunktion:
-
Oben war schon angedeutet worden, dass Funktionsgraphen nicht "rückläufig" sein dürfen.
Keine Ahnung, ob es bei Brio auch Kreuzungen gibt. Aber die "Rückläufigkeit" ist da auch mit Brücken möglich:
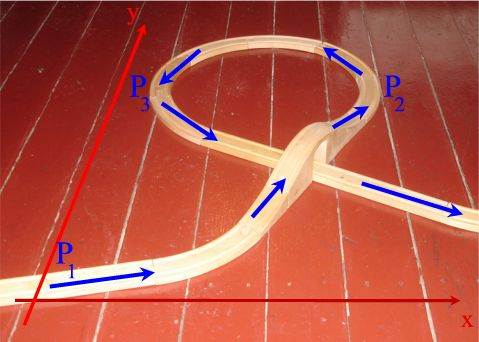
Hier liegt kein Funktionsgraph vor, weil (mindestens) einem x mehrere y-Werte zugeordnet werden, nämlich y1 und y2 und y3.
"Rückläufig" heißt dabei, dass man, wenn man - wie üblich - mit der "Fahrt" in P1beginnt
erst (bis P2) nach rechts,
dann (bis P3) nach links
und danach wieder nach rechts fährt:
Mich interessiert da ja eigentlich wieder das konkrete Konstruktionsprinzip, also hier die Brücke (statt einer Kreuzung), bei der die "SchnittpunktE" übereinander liegen, die Bahn also - im Gegensatz zu üblichen Funktionsgraphen - dreidimensional wird.
Aber ich muss gestehen, dass ich da (noch) keine spezifische "Aussage" (einen pädagogischen Vorteil?) sehe.
(Germanisten neigen ja dazu, alles [also auch Druckfehler] zu interpretieren - und sollten sich da vielleicht ein bisschen mehr zurückhalten.)
Einige Tage später erscheint mir eine Kreuzung doch "sinniger" als eine Brücke, denn bei einer Kreuzung wird das Verbot der Rückläufigkeit dadurch "greifbar", dass (wie bei Weichen) Züge zusammenstoßen können oder ein langer Zug "sich selbst in den Schwanz beißen" kann.
-
Eben war schon von einer "Fahrt" die Rede: der entscheidende Vorteil der Brio-Bahn
(oder ähnlicher Modellbahnen)
besteht
(auch gegenüber der anfangs genannten biegbaren Schiene)
darin, dass man einen Zug drauf setzen und
den (Nicht-)Funktionsgraphen wortwörtlich "er-fahren"
kann. Dann wird SchülerInneN beispielsweise viel leichter deutlich, wann eine Rechts- bzw. eine Linkskurve, also auch ein Wendepunkt vorliegt.
-
Brio-Bahnen sind auch sehr gut geeignet, um die Probleme der (Nicht-)Stetigkeit und der (Nicht-)Differenzierbarkeit anzudeuten:
Im Fall
(hier und im folgenden Bild spare ich mir das Koordinatensystem)liegt wegen der Lücke eine Unstetigkeit vor - die gerade bei einer Eisenbahn "kontraproduktiv" ist.
Im Fall
liegt eine Spitze, also Nicht-Differenzierbarkeit vor - die auch wieder bei einer Eisenbahn völlig unsinnig ist: ein Zug hat keinen Platz, nach rechts abzubiegen, sondern fällt dabei oben runter.
-
An Brio-Bahnen kann (und sollte) man vollständige "Kurvendiskussionen" durchführen, d.h.
zwar noch nicht spezielle Eigenschaften berechnen (da ja keine Funktionsgleichungen vorliegen),
aber dennoch schon alle speziellen Eigenschaften beschreiben,
und das lange vor der Oberstufe, in der "Kurvendiskussionen" erstmals ausdrücklich Thema sind.
-
Sogar ein spezifischer Nachteil der Briobahn (eine Grenze des Modells) ließe sich zwecks "tieferer" mathematischer Erkenntnis ausschlachten: alle Kurvenstücke der Briobahn sind kreissegmentförmig, haben also (anders als etwa eine Parabel) immer dieselbe Krümmung - und doch ergeben sich schon innerhalb eines einzigen Kurvenstücks verschiedene Steigungen!
-
Über alles bislang Gesagte, eher "Durchschnittliche" hinaus ermöglicht aber die Brio-Bahn (oder eine ähnliche Modellbahn) noch eine mathematisch (!) ungemein faszinierende Möglichkeit, wenn man da eine elektrische Lock mit einer Lampe vorne fahren lässt.
Der Strahl der Lampe ist immer gerade die Halb-Tangente an die Bahn, zeigt also die Steigung in jedem Punkt an.
Wenn diese Steigung nicht gerade konstant ist, also ein Geraden-Teilstück vorliegt, ändert sie sich kontinuierlich, womit wieder - hochtrabend gesagt - eine "Limes-Propädeutik" stattfindet.
Das Experiment sei noch weiter gedacht: wenn man statt der eingebauten Lampe etwa einen "Laser-Pointer" auf der Lokomotive befestigen würde, könnte man das Experiment in einem derart stockdusteren Raum durchführen, dass weder die Lok (oder genauer: nur der AustrittsPUNKT des Laserstrahls) noch die Schienen sichtbar sind, sondern nur der Punkt des Laserstrahls an den umliegenden (ihrerseits ansonsten unsichtbaren) Wänden.
Damit nicht Verzerrungen durch die Architektur des Raumes eintreten, könnte man einen runden Raum wählen bzw. um die Modelleisenbahn eine runde "Umzäunung" stellen.
In einem rechteckigen oder quadratischen Raum würde hingegen besser deutlich werden, dass der Strahl niemals auf die linke Wand fällt, da Funktionsgraphen ja (s.o.) niemals rückläufig sind.
Was könnte man denn nun bei der vorgeschlagenen "Laser-Konstruktion" überhaupt noch sehen:
eben nicht mehr, wann die Lok in einem angeblich so wichtigen Maximum oder Minimum (einem Absolutwert) ist,
sondern "nur" noch (was aber letztlich viel wichtiger ist!), dass
der Lichtpunkt an der Wand stillsteht, was auf gleichbleibende Steigung, also ein gerades Schienenstück schließen lässt,
oder dass er sich bewegt, was auf sich verändernde Steigung, also auf ein krummes Schienenstück schließen lässt.
In diesem Fall b. ließe sich sogar noch genauer differenzieren:
wenn der Lichtpunkt an der Wand sich nach links bewegt, liegt eine Schienen-Linkskurve vor,
wenn er sich nach rechts bewegt, liegt eine Schienen-Rechtskurve vor.
Und wenn die Bewegung des Lichtpunkts an der Wand urplötzlich von einer Links- in eine Rechtsbewegung übergeht (oder umgekehrt), liegt ein Wendepunkt vor!
Des weiteren könnte man aus der zunehmenden bzw. abnehmenden Geschwindigkeit des Lichtpunkts auf zunehmende bzw. abnehmende Steigung der Schienen schließen.
(Wohlgemerkt:
die Bewegung des Lichtpunkts an der Wand beschleunigt oder verlangsamt sich [oder er bleibt evtl. sogar stehen],
während [obwohl?] die Lok immer gleich schnell fährt!)
Anders gesagt:
hätten wir bei diesem Experiment
in Reinkultur: außer Bewegung (und Stillstand) bliebe gar nichts mehr übrig ("reduce to the max"),
könnte man allein aus der (Nicht-)Bewegung des Lichtpunkts auf fast alle Eigenschaften des Schienenverlaufs rückschließen - ein Experiment, das zwar erhebliches Abstraktionsvermögen voraussetzt (oder erst einübt?), aber dennoch schon in der Mittelstufe wichtig wäre, um SchülerInnen Grundeigenschaften von Funktions(graphen)verläufen klar zu machen.
(Ein ganz praktisches Problem sehe ich aber darin, dass die Lok
einerseits ziemlich schnell fahren müsste, damit die Beschleunigungen des Lichtpunkts auch sehr deutlich würde,
andererseits aber sehr langsam fahren und ggf. auch zu stoppen sein müsste, damit man Zeit hat, auf die Eigenarten des Schienenverlaufs rückzuschließen.
Aber es wäre ja möglich, den Schienenverlauf mehrfach - einmal schnell, einmal langsam - abzufahren.
Oder man könnte ja sogar mit "eindeutigen" Teilstücken anfangen, also z.B.: "Was passiert mit dem Lichtpunkt bei einer Rechtskurve/einer Linkskurve/einem Wendepunkt?")
Die Bewegung des Lichtstrahls illustriert etwas mathematisch durchaus schon Anspruchsvolles, aber eben doch auch elementar Wichtiges, nämlich
die zweite Ableitung f !
(die man in einer Mittelstufe ja noch nicht so nennen muss),d.h. nicht so sehr die Steigung, sondern die änderung der Steigung
(die Steigung der Steigung):
wichtig sind nicht (nur) absolute Werte, sondern (auch und vielleicht sogar mehr noch) relative Veränderungen.
(Nur Kurzsichtige orientieren sich allein an Absolutwerten [der für jede Zukunft blinden Gegenwart], feiern also beispielsweise bei einem Gewinnmaximum, obwohl "Maximum" doch nur bedeutet, dass es danach wieder bergab geht.)
Wichtig ist also beispielsweise
Man könnte auch noch die Koordinatenachsen mit auch in der Dunkelheit leuchtendem Klebe-Leuchtband
(am besten quer durch die Klasse) markieren, und wenn man lustig ist, die Bewegung auch noch vertonen, also z.B.
steigend: zunehmend höherer Ton,
fallend: zunehmend dunklerer Ton, d.h. auch
im absoluten Maximum auch der höchste Ton,
im absoluten Minimum auch der tiefste Ton
(man versteht also den Funktionsgraphenverlauf regelrecht als Notenschrift),
Linkskurve: zunehmend lauter,
Rechtskurve: immer leiser
(womit
ein Wendepunkt, an dem eine Links- in eine Rechtskurve übergeht, am lautesten,
und einer, in dem umgekehrt eine Rechts- in eine Linkskurve übergeht; am leisesten [völlige Stille?] wäre).
Wenn man den Aufwand noch steigern will, kann man (in einer späteren Phase) auch noch eine Nebelmaschine anwerfen, so dass nicht nur die Endpunkte der Tangenten, sondern die Tangenten selbst (oder genauer: die Halbgeraden) sichtbar werden.
Der Aufwand mag einem mit einigem Recht als allzu groß erscheinen, und doch ist all das nicht einfach nur Schnickschnack, sondern es hat durchaus direkt etwas mit der dargestellten Mathematik zu tun
... und überhaupt bleibe ich der Meinung, dass Mathematik (zumindest für Anfänger) viel mehr als üblich mit allen Sinnen genossen (?!) werden sollte:
Wer (Mathematik) nicht "spüren" kann,
muss anfassen;
wer nicht anfassen kann,
muss (zusätzlich) sehen;
wer nicht sehen kann,
muss (zusätzlich) hören.