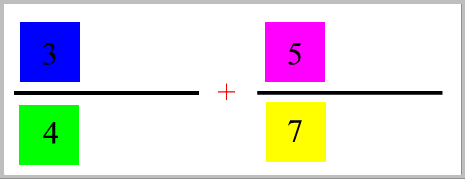
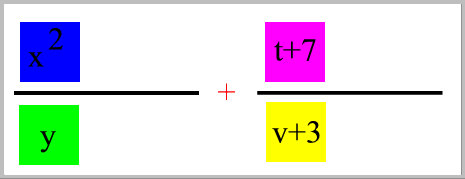
die Bruchrechenraster
Das Wort "Rasterfahndung" scheint mir bei dem, was ich hier zeigen möchte, durchaus treffend:
"Die Rasterfahndung ist ein in den 1970er Jahren infolge der vergeblichen Fahndung nach den RAF-Terroristen vom damaligen BKA-Präsidenten Horst Herold entwickeltes Verfahren zur vernetzten Durchsuchung von Datenbeständen. Dabei werden bestimmte Personengruppen aus öffentlichen oder privaten Datenbanken herausgefiltert, indem man nach Merkmalen sucht, von denen man annimmt, dass sie auch auf die gesuchte Person zutreffen. Ziel ist es, die Gruppe der zu überprüfenden Personen einzuschränken, da es im Gegensatz zu einer konventionellen Fahndung keine bekannte Zielperson gibt."
(zitiert nach  ; farbliche Hervorhebung von mir, H.St.)
; farbliche Hervorhebung von mir, H.St.)
Bei meinem Vorhaben wird allerdings nicht nach typischen Merkmalen von Terroristen oder Verbrechern gesucht, sondern nach solchen von Standardrechnungen und insbesondere Bruchrechnungen.
Vorerst aber zwei typische Raster von Nicht-Bruchrechnungs-Rastern:
Gesucht sind also fertige Raster, mittels derer möglichst schnell herausgesiebt werden kann, was zu tun ist

bzw. in die man nur noch konkrete Werte (s.u. C.) einsetzen muss.
Ich bin der festen Überzeugung, dass man am besten nicht allein die verbalen Merksätze
(z.B. "zwei Brüche werden addiert,
kennt, sondern auch ein optisches Raster vor Augen hat oder sogar zwischenzeitlich mit greifbaren Rastern (Schachteln) arbeitet
(vgl. 

 ).
).
Die rein verbalen Merksätze sind nämlich teilweise zu ungenau bzw. - wie sich allzu oft im Unterricht zeigt - irreführend
(z.B. bedeutet "und dann die Zähler addiert und den Nenner beibehält" genau genommen [und zur Abgrenzung beispielsweise gegenüber der Bruchmultiplikation]: "und dann die beiden Zähler über einem Bruchstrich addiert und den Nenner einmal beibehält").
-
Hier also die allerersten, noch völlig abgenagten, aber gerade deshalb schon aufschlussreichen Bruchrechenraster:
Dazu aber vorweg eine allgemeine Anmerkung: weil selbst die schlausten MathematikerInnen nicht direkt mit Brüchen, sondern nur mit ganzen Zahlen rechnen können,

und
-
die Bruchaddition +
 =
=
=  =
=
= 
Das Wichtige daran ist
(soviel sei schon im Vergleich mit den anderen Bruchrechnungen vorweggenommen):
-
die Bruchaddition ist in der Regel
(wenn die Brüche nicht schon anfangs "gleichnamig" sind, also denselben Nenner haben)
ein dreistufiges Verfahren,
-
am Ende wird nur noch im Zähler addiert.
-
Analog gilt für die Bruchsubtraktion -
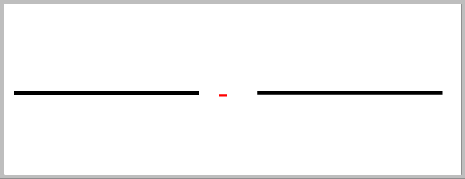 =
=
= 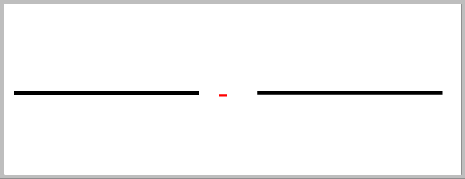 =
=
= 
-
die Bruchmultiplikation •
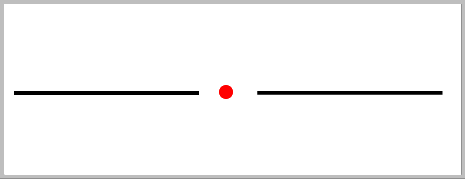 =
=
= 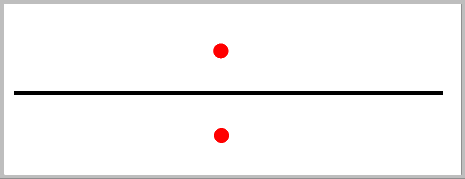
Anders als Bruchaddition und -subtraktion gilt also für die Bruchmultiplikation:
-
sie ist immer ein zweistufiges Verfahren,
-
am Ende wird sowohl im Zähler als auch im Nenner multipliziert.
-
die Bruchdivision :
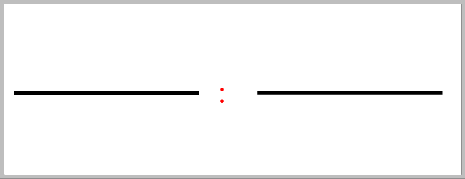 =
=
=  =
=
= 
Dabei wird im ersten Schritt die schwierige Bruchdivision auf die aus 3. bekannte einfachere Bruchmultiplikation zurückgeführt. Daraus folgt:
-
Da die Bruchmultiplikation dann noch zweischrittig ist (vgl. 3.), ist die Bruchdivision insgesamt dreischrittig.
-
Aus der anfänglichen Division wird eine Multiplikation und
-
am Ende wird sowohl im Zähler als auch im Nenner multipliziert.
Nachteil dieser ersten Raster ist, dass noch völlig unklar bleibt, wie innerhalb der Brüche mit welchen Elementen gerechnet wird. Daher nun
-
schon ein bisschen vollständigere Raster:
-
die Bruchaddition +
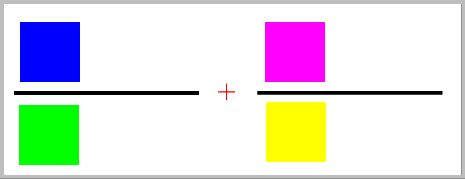 =
=
= 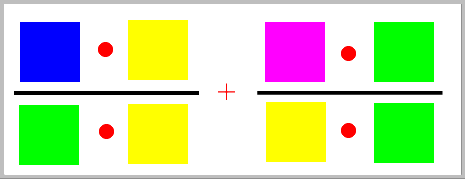 =
=
= 
Dabei wird deutlich:
um die beiden anfänglichen Brüche gleichnamig zu machen, also zu erreichen, dass sie denselben Nenner • haben
(falls das nicht von Anfang an der Fall ist),
müssen - obwohl die Bruchaddition vorliegt - zwischenzeitlich Multiplikationen
(allerdings glücklicherweise nicht mehr von Brüchen, sondern von einfachen Zahlen!)
durchgeführt werden.
(Die beiden anfänglichen Brüche müssen auf den "Hauptnenner" gebracht werden, was üblicherweise dadurch geschieht, dass man das Kleinste Gemeinsame Vielfache der beiden ursprünglichen Nenner berechnet.
Da hier aber noch keine konkreten Zahlen vorliegen, ist der Hauptnenner nur durch Multiplikation der beiden kompletten ursprünglichen Nenner findbar: •
Das hat immerhin den Vorteil, dass es auch funktioniert, wenn in die farbigen Felder statt Zahlen Variable oder Terme eingesetzt werden [s.u. C.].)
Merke: eine direkte Addition zweier Brüche ist überhaupt nur möglich, wenn sie bereits gleichnamig sind bzw. gemacht worden sind. Der allererste Blick bei einer Bruchaddition (vor jeder Rechnung!) sollte also immer untersuchen, ob die Gleichnamigkeit bereits vorliegt oder noch herzustellen ist.
(Es ist ähnlich wie bei Dreiecken: wenn überhaupt irgendein Dreieck auftaucht, achte man zu allererst darauf, ob es rechtwinklig ist.)
-
die Bruchsubtraktion - funktioniert dann analog zur Bruchaddition folgendermaßen:
 =
=
=  =
=
= 
-
die Bruchmultiplikation •
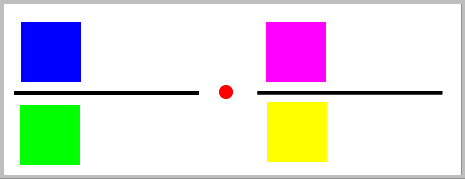 =
=
= 
Im Vergleich mit der Bruchaddition und -subtraktion ist also an der Bruchmultiplikation bemerkenswert, dass
(wenn auch nicht mehr der Multiplikation zweier Brüche, sondern der Multiplikation von jeweils zwei Zahlen),
also keine andere Rechenart ins Spiel kommt,
(und deshalb ja eben ist die Bruchmultiplikation nur zweischrittig),
(während bei der Bruchaddition bzw. -subtraktion nur im Zähler addiert bzw. subtrahiert wird, der Nenner hingegen aber nur einmal "beibehalten" wird).
-
die Bruchdivision :
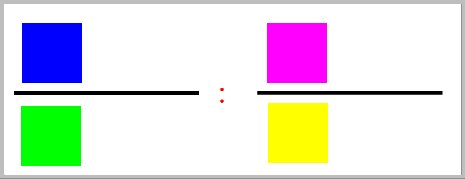 =
=
= 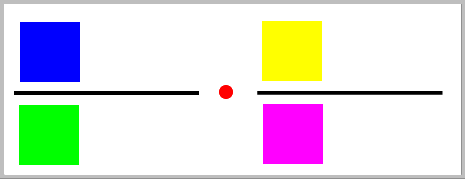 =
=
= 
Bemerkenswert bei der Bruchdivision ist, dass sie im ersten Schritt auf eine Bruchmultiplikation zurückgeführt
(also durch eine andere Rechenweise ersetzt)
wird, indem mit dem Kehrbruch des zweiten Bruchs multipliziert wird, während der erste Bruch unbedingt unverändert bleibt.
(Wie auch bei den anderen Bruchrechenarten soll hier nicht erklärt werden, warum das so ist.)
Die schwierige Division wird also auf eine einfachere Multiplikation zurückgeführt und dann im nächsten Schritt wie in 3. weitergerechnet.
-
Und jetzt endlich, nachdem die Raster die jeweiligen grundlegenden Prinzipien klar gemacht haben, kann man auch nach Lust und Laune Zahlen oder sogar komplexere Terme einsetzen, also z.B. bei der Bruchaddition
Beim Einsetzen von Termen sei allerdings dringend darauf hingewiesen, dass man, wenn man die farbigen Kästchen weglässt und zur üblichen mathematischen Schreibweise übergeht, Klammern
(also das mathematische äquivalent der Kästchen)
um die Terme setzen muss.
![]() ; farbliche Hervorhebung von mir, H.St.)
; farbliche Hervorhebung von mir, H.St.)


 =
=
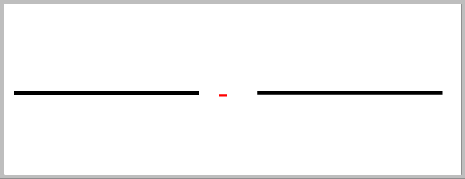 =
=
 =
=
 =
=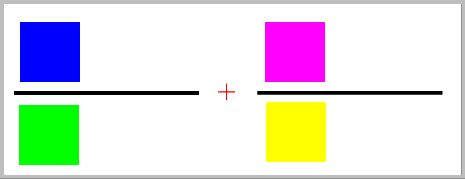 =
= =
=
 =
= =
=
 =
=
 =
= =
=