
Bruchrechenregeln veranschaulichen

Bruchrechenregeln veranschaulichen
Thema hier sind die (nur!) drei Regeln, nach denen jeweils zwei Brüche addiert / subtrahiert, multipliziert oder durcheinander dividiert werden
(wobei das Erweitern und Kürzen von Brüchen vorausgesetzt wird):

Da frage ich mich
, in welcher Unterrichtsphase eine anschauliche Vermittlung hilfreich sein kann, also
, wie genau Veranschaulichungen in den beiden Phasen aussehen sollten.
Zu 1., also der Herleitung der Bruchrechenregeln
Es gibt meiner Meinung nach auch Grenzen der Anschaulichkeit. So sollten die Schüler
 ,
, ![]() •
• ![]() bedeutet "
bedeutet "![]() von
von ![]() "
"
 bzw. abstrahiert
bzw. abstrahiert  :
: 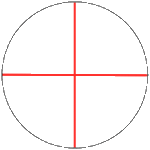 ,
, ;
;
 in 8 gleich große Teile):
in 8 gleich große Teile): nun in 8 gleich große Teile
nun in 8 gleich große Teile  ,
, .
. =
=  .
. in die
exakt gleich großen 8 „Tortenstücke“
in die
exakt gleich großen 8 „Tortenstücke“  zu zerlegen? Das
gelingt nämlich nur, wenn man den ganzen Kuchen
zu zerlegen? Das
gelingt nämlich nur, wenn man den ganzen Kuchen  in 32stel zerlegt und davon 9 nimmt:
in 32stel zerlegt und davon 9 nimmt:  .
.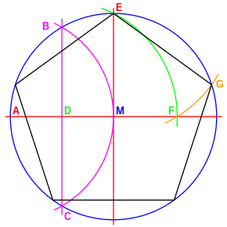 aussieht.)
aussieht.)
 bzw. abstrahiert
bzw. abstrahiert 
 horizontal im 4 gleich
große Streifen
horizontal im 4 gleich
große Streifen 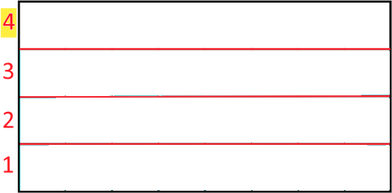 ,
,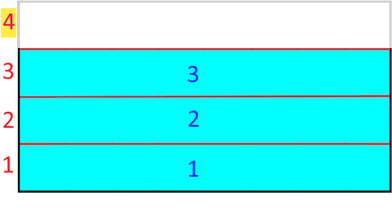 ;
;
 vertikal in 8
gleich große Streifen
vertikal in 8
gleich große Streifen 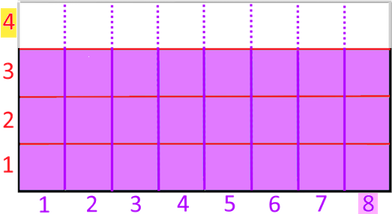 ,
,
 ;
;
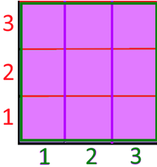 besteht aus 3 •
3 = 9
Quadraten, das Anfangsrechteck
besteht aus 3 •
3 = 9
Quadraten, das Anfangsrechteck  hingegen aus 4
• 8
= 32 Quadraten;
hingegen aus 4
• 8
= 32 Quadraten;
 =
=  bzw.
bzw.
 ,
,
(vgl. 8 :
2 bedeutet "wie oft passt die 2 in
die 8?", nämlich 4 mal; aber die 8 passt
![]() mal in die 2 , was doch arg unanschaulich
ist: wie soll ein Elefant in eine Maus passen?; und doch passt ein
Teil des Elefanten exakt in die Maus:
mal in die 2 , was doch arg unanschaulich
ist: wie soll ein Elefant in eine Maus passen?; und doch passt ein
Teil des Elefanten exakt in die Maus:
 ).
).
 in 4
gleich große Teile
in 4
gleich große Teile  ,
, ;
;
(also nicht [wie oben bei der Bruchmultiplikation]
den ![]() -Kuchen
-Kuchen  !)
!)
in 8 gleich große Teile 
 oder
oder 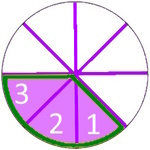 .
. =
=  , d.h.
, d.h.Das ist ein schön einfaches Ergebnis, für das allerdings künstlich gesorgt wurde:
Das ist aber keine anschauliche Herleitung mehr
(und sie funktioniert sowieso nur so einfach, wenn [wie hier] entweder die Zähler oder aber die Nenner der beiden Brüche identisch sind).
Zudem hat die
anschauliche Herleitung  =
=  , also
von
, also
von ![]() :
:
![]() = 2 ,
einen (ersten) entscheidenden Nachteil:
= 2 ,
einen (ersten) entscheidenden Nachteil:
es bleibt unklar, dass und warum man
![]() .
.
Oder kurz
![]() .
.

Der entscheidende Nachteil der Kuchendarstellungen von Brüchen ist aber, das sie immer nur für konkrete Brüche
(z.B. ![]() und
und ![]() )
)
funktionieren und somit für jede neue Bruchauswahl neu durchgeführt werden müssten
(was z.B. bei ![]() und
und ![]() enorm aufwändig wäre).
enorm aufwändig wäre).
(wie oft üblich)
mit stumpfer Rechen-
und Rezept-„Mathematik“ abzuspeisen  ,
,
Selbst wenn diese Herleitungen in späteren Schuljahren
(oder dem späteren Leben der Schüler)
nie wieder benötigt werden, haben sie oftmals ihre Existenzberechtigung, denn sie sind

Die oben vorgeführten Veranschaulichungen von Bruchrechenregeln halte ich aber nurmehr für kontraproduktiv, da
(Allerdings sind die Bruchrechenregeln im selben Augenblick, in dem man die sie sicher (innermathematisch) anwenden kann, mathematisch uninteressant und nur noch Handwerkszeug.)
Besonders wichtig wird dieses Handwerkszeug im weiteren Schulverlauf bei (Funktions-) Gleichungen, die enorm wichtig bis ins Abitur wie überhaupt in der gesamten Mathematik sind.
Ein ganz simples Beispiel zur oben behandelten Bruchdivision ![]() :
:
![]() = 2 :
= 2 :

Da wird
stumpf ein Bruchrechengesetz angewandt und denkt keiner mehr
an  und
und  und wie sie sich zueinander verhalten.
und wie sie sich zueinander verhalten.
Was also an der Bruchrechnung ist innerhalb der (Schul-)Mathematik wichtig?
Zu a.: es muss klar werden
(und das scheint mir in Schulen oftmals doch zu kurz zu kommen)
dass der Zahlenstrahl durch die massenhaften
rationalen Zahlen zwischen den natürlichen Zahlen
![]() .
.
 wird, so dass man die Vermutung aufstellen kann
wird, so dass man die Vermutung aufstellen kann
(oder stillschweigend unterstellt),
dass er dadurch "stetig" voll ist, es also keine Lücken mehr gibt
Und da sollte im Unterricht schon der Wegweiser
 zur ersten
nicht-rationalen Zahl aufgestellt
zur ersten
nicht-rationalen Zahl aufgestellt
oder sogar bereits eine nicht-rationale konstruiert werden, also z.B. 0, 1 2 1 22 1 222 1 2222 ...
Zu 3., also der Herleitung der Bruchrechenregeln z.B. mittels  :
:  = 2 :
= 2 :
ich habe oben mit viel Mühe "Kuchen"-Veranschaulichungen dargestellt, um gerade damit zu zeigen, dass sich die Mühe kaum lohnt.
Zu 2., also der Anwendung der (vorher hergeleiteten?) Bruchrechengesetze
Vorweg: eines meiner Standardmittel für
Veranschaulichungen sind Alltagsdinge wie z.B. oben  und
und  .
.
Zwar wurden diese Kuchen oben schnell zu  und
und  abstrahiert,
aber sie sind bei den nachfolgenden Überlegungen doch hoffentlich doch im
Hinterkopf geblieben: die Alltagsdinge und -vorgänge sind also
abstrahiert,
aber sie sind bei den nachfolgenden Überlegungen doch hoffentlich doch im
Hinterkopf geblieben: die Alltagsdinge und -vorgänge sind also
Veranschaulichungen
aber keine echten außermathematischen Anwendungen:
z.B. ![]() von
von  =
=  ist eine
Überlegung, die wohl niemals beim realen
Kuchen-Verteilen stattfindet.
ist eine
Überlegung, die wohl niemals beim realen
Kuchen-Verteilen stattfindet.
Im Folgenden geht es nun aber
nicht mehr darum, z.B. die Bruchrechenregel
![]() herzuleiten,
herzuleiten,
sondern darum, sie für verschiedenste Zahlen a, b, c und d anzuwenden.
Um diese Anwendung zu trainieren, wähle ich hier
(wie auch gerne bei Funktionen)
zwei weitere Metaphern:
Maschinen
 , die mit
beliebigen Eingaben immer dasselbe durchführen
, die mit
beliebigen Eingaben immer dasselbe durchführen
(z.B. verdoppelt die Funktion f: y = 2 • x jedes eingegebene x ),
Kartons
![]() (im folgenden
Geschenkboxen), in die jede beliebige Zahl eingegeben werden kann, deren
Inhalt also letztlich egal (unsichtbar) ist.
(im folgenden
Geschenkboxen), in die jede beliebige Zahl eingegeben werden kann, deren
Inhalt also letztlich egal (unsichtbar) ist.
Kommen wir damit also zur
Veranschaulichung der
(bereits hergeleiteten) Bruchrechenregeln  :
:
 :
:

Als Gleichung aus Standbildern:  =
= ,
,
also z.B.

oder
 .
.
die Bruchaddition (und analog die Bruchsubtraktion)

 :
:
Normalerweise ist die (schriftliche) Addition einfacher als die (schriftliche) Multiplikation. Anders aber bei der Bruchrechnung:
um Brüche überhaupt addieren zu können, müssen sie
 ) haben
) haben 
Als Gleichung aus Standbildern:  =
=
 , Fehlerquelle: bei der Bruchaddition
, Fehlerquelle: bei der Bruchaddition
 ,
,

 :
: 
Als Gleichung aus
Standbildern:

Am Beispiel der Bruchdivisonsmaschine wird der Vorteil solcher "Filmchen" deutlich: die Bruchrechenregel ist da
eine Tätigkeit (der Maschine) bzw. ein "stetiger" Prozess,
statt eines "diskreten" Sprungs wie in
 .
.
Besser als die hier benutzten „Filmchen“ sind normalerweise echte kleine Maschinen,
Ein Beispiel: die Bruchmultiplikation  sähe als simple Lego-Maschine z.B. so aus:
sähe als simple Lego-Maschine z.B. so aus:

(Am besten wäre es aber, wenn die Schüler solche Maschinen selbst bauen würden: beim Bauen würden sie die Bruchrechengesetze besser verstehen.)
Der Vorteil solch einer echten Maschine ist, dass da
nicht nur die Maschine etwas tut,
sondern die Schüler selbst etwas tun.
Diese erste Umsetzung als Maschine hat aber im Vergleich
mit  den
Nachteil, dass
den
Nachteil, dass
der Multiplikationspunkt nicht langsam in die beiden Multiplikationspunkte aufgespaltet wird
und die anfänglichen Bruchstriche nicht zu einem einzigen Bruchstrich zusammenwachsen.
Mit einer komplizierteren Mechanik könnte man an der Maschine auch diese Effekte ergänzen, aber
welcher Lehrer hat schon die passenden Lego-Teile und die Zeit, „eben mal kurz“ die nötige Mechanik zu ersinnen?,
ich bin zu faul, die entsprechende Mechanik (auch für die anderen Bruchrechengesetze) zu entwickeln.