Bruch- und Prozentveranschaulichung mittels
(ob, warum, wie, wann)

frischweg (arg allgemein) abgelästert
massenhaft Fragen
ganz wenige Antworten

frischweg (arg allgemein) abgelästert

Vorweg: es gibt selbstverständlich auch MathematikleherInnen, die nicht folgender pointierter Beschreibung entsprechen. JedeR suche sich den Schuh aus, der ihr/ihm passt!

Die allermeisten MathelehrerInnen sind nicht in der Lage, "ausdrücklich" - und zwar pädagogisch! - zu reflektieren, d.h. entweder mündlich oder schriftlich

(fachlich können sie es hingegen - z.B. über Lösbarkeit und Lösungswege - stundenlang):

• Tun sie es wirklich (auch in ihrem Kopf) nicht, oder können sie es "nur" nicht ausdrücken?

(... etwa so, wie es ja immerhin die Vermutung gibt, dass bei Männern [und die stellen nach wie vor einen Großteil der MathematikerInnen] linke und rechte Gehirnhälfte schlechter verbunden seien und die Männer deshalb den [durchaus vorhandenen!?] "Gefühlen" aus der rechten Gehirnhälfte keinen oder nur schwer Ausdruck über die linke Gehirnhälfte geben könnten: sie habens zwar, aber ersticken dran?

Viele - und das sage ich ohne jeden Vorwurf! - MathelehrerInnen sind absolut illiterat, seis, dass sie

• nie lesen

[keine "richtige" Literatur, sondern höchstens den "Focus"],

• keinen Text, der länger als eine Email ist, lesen können,

• keinen längeren und differenzierteren Text schreiben können und überhaupt größte [teilweise offen eingestandene] Ausdrucksschwierigkeiten haben.

Und dann gibts noch solche unter ihnen, die regelrecht stolz darauf sind und beispielsweise Literatur als "nur Fiktion", "unlogisch" und "nicht anwendbar" denunzieren: die Ignoranz ist durchaus beidseitig, es wird nicht nur - wie sonst oft behauptet - mit "schon meine Oma konnte keine Mathematik" angegeben.)

• Verstehen sich viele MathelehrerInnen überhaupt (auch) als PädagogInnEn, d.h. gibt es für sie überhaupt etwas pädagogisch zu reflektieren? Oder folgen sie vielmehr allein der Fachlogik - und verstehen sich auch nur als Fachleute?

Ich bemerke (sogar) bei MathelehrerInneN inzwischen zwar durchaus vermehrt die Bereitschaft zu neuen (???), "offeneren" Methoden

(bzw. man kommt "wohl leider" nicht mehr ganz drumherum, hofft aber insgeheim, dass das eine schnell erledigte Modetorheit ist?),

aber diese Methoden werden dann oftmals "klotzartig" durchgeführt, aber nie detailliert reflektiert (vgl. etwa ).

(Kommt hinzu, dass Reflexion allzu oft mit [Negativ-]Kritik gleichgesetzt wird:

• wer eigene Sachen reflektiert und evtl. sogar ein [partielles] Misslingen von Vorhaben zugibt, gibt sich eine Blöße [big brother is watching you, d.h. die Bezirksregierung und das halbe Kultusministerium liest mit],

• eine Krähe kratzt der anderen [KollegInnEn] kein Auge aus,

• und in der Tat gibt es einige ewige Schlaumeier, die jedes Ergebnis anderer LehrerInnen niederreißen, um sich auf diese Art zu profilieren; man beachte mal die Hahnenkämpfe und das Fachterminologie-Dropping, wenn gestandene MathelehrerInnen konferieren!)

Zuguterletzt richtig tief (und arrogant) durchgelästert:

vielen (Mathe-)LehrerInneN fehlt es (nicht nur fachlich) auch an geistigem Horizont über die Schulbücher hinaus:

"Wenn wir von einer [Mathe-]lehrerin sagen, sie sei gebildet, meinen wir gerade nicht ihre [Mathe-]kenntnisse."
(frei nach Ulf von Rauchhaupt)

Ich halte zwar durchaus viel von der Fachausbildung von LehrerInnen im Studium und befürchte, dass eine solide fachliche Ausbildung demnächst in den reformierten Lehramtsstudiengängen zu kurz kommen wird.

Dennoch: LehrerInnen lernen in der klassischen Ausbildung ja auch nie konkretes pädagogisches Reflektieren:

1. sowieso nie während meines Studiums in der universitären Fach"didaktik": da wurde ja oftmals nur ein "Fach"-Professor ausgelost bzw. verdonnert, ein "nun mal leider unvermeidbares" Fachdidaktikseminar abzuhalten, und dementsprechend fern aller schulischen Wirklichkeit war es dann auch;

2. zumindest in meinem Referendariat wurden wir nur mit schlauen Theorien zugeknallt - und hinterher bei Nichteinhaltung damit "hingerichtet"; merke: wenn im Unterricht etwas schief läuft, ist immer der Referendar schuld;

3. und auch auf Fortbildungen, Fachtagungen und Fachkonferenzen habe ich nie konkrete pädagogische Überlegungen erlebt.

Mein Vorhaben im Folgenden ist seinerseits durchaus "päda"gogisch: gewissen MathelehrerInneN exemplarisch erste (massenhaft) Fragen vorzuführen

(und nur ganz wenige Antworten, und zwar 

1. , weil ich auch nicht auf jeden Pott nen Deckel, d.h. auf jede Frage eine [die einzig richtige] Antwort habe,

2. , weil Antworten oftmals von der konkreten Situation [Klasse, EinzelschülerInneN ...] abhängen

[es ist ja gerade der zentrale Nachteil vieler Standardmethoden, dass letztere pauschal - und geradezu als Patentrezepte - (Schein-)Antworten geben bzw. suggerieren],

3. , weil es mir hier vor allem darum geht, überhaupt erst mal das Fragen zu lernen - und ich darauf vertraue, dass sich aus den Fragen dann auch oftmals schnell Antworten ergeben werden. Ich verstehe Fragen nicht als Eingeständnis der Schwäche oder prinzipieller Unsicherheit, sondern als Aufgaben [griech. problema] - in diesem Fall an die LehrerInnen).

"Exemplarisch" aus zwei Gründen:

• man kann nur konkret werden, wenn man sich "weise" auf ganz wenig beschränkt

(jedes komplette "Stationenlernen" ist schon viel zu groß);

• weil LehrerInnen viel zu sehr im Stress stehen, als dass sie jede einzelne Aufgabe reflektieren könnten. Sie sind weitgehend darauf angewiesen, sich auf fertige (und oftmals fragliche; vgl. ) Vorgaben zu verlassen.

Abgesehen von veränderten Grundeinstellungen

(z.B.: ich bin nicht der große Fachmann, der SchülerInneN sagen kann, wos lang geht)

vertraue ich doch am meisten darauf, dass exemplarische Reflexionen sich "von selbst" ausbreiten.

massenhaft Fragen

Mein Thema hier ist also

Bruch- und Prozentveranschaulichung mittels kommunizierender Röhren ... ob, warum, wie, wann?

(Einer ersten Implikation möchte ich dabei nicht weiter nachgehen bzw. sie nicht weiter hinterfragen: nämlich dass das Röhrenexperiment, wenns denn überhaupt geeignet ist [s.u.], gleichermaßen für die Bruch- UND die Prozentveranschaulichung hilfreich ist:

• "³/₄ voll" ist halt dasselbe wie "zu 75 % voll",

• überhaupt sind Prozente nur eine andere Schreibweise von Brüchen

• und gehts in beiden Fällen [das aber wird durchaus noch wichtig. s.u.] um relative Anteile.

Ebenfalls undiskutiert soll hier bleiben, ob SchülerInnen die Bruch- und Prozentrechnung überhaupt brauchen [wozu, wieviel?], seis innermathematisch bzw. im Hinblick auf die weitere mathematische Schul"karriere", seis im "richtigen" Leben.)

Die farblichen Markierungen implizieren bereits zu hinterFRAGENde Vorentscheidungen:

1. Was ist mit "Veranschaulichung" überhaupt gemeint? Brauchen SchülerInnen sie überhaupt, um später - und darauf läuft doch der meiste (konventionelle) Matheunterricht hinaus - rechnen zu können? Gibt es SchülerInnen, die von einem anderen als dem "visuell-haptischen" Lerntyp sind, denen Modelle also rein gar nichts bringen - und wie "hilft" man ihnen? Was genau sollen SchülerInnen durch Veranschaulichungen lernen und hinterher können (z.B. Unterscheidung relativer/absoluter Anteil; [Un-]Abhängigkeit von der Form; s.u.)? Was kann man bei SchülerInnen aus dem "Alltagsleben" voraussetzen, also im Unterricht weglassen oder umgekehrt in ihn einbeziehen und darauf aufbauen? Alles? Bei allen? Wenn zwar bei einigen, aber nicht allen: wie geht man mit dieser Diskrepanz um? Brauchen erstere überhaupt noch Modelle ("kommunizierende Röhren", "ob")? ("Wie") Nehmen SchülerInnen überhaupt Brüche und Prozente vor jedem Unterricht wahr? Welche typischen Probleme, Missverständnisse und Fehler gibt es da?

(EinE altgedienteR LehrerIn ahnt diese Probleme voraus; ist es da ratsam oder ganz im Gegenteil kontraproduktiv, diese Probleme vorwegzunehmen bzw. vorweg zu entschärfen?)

Wie geht man mit falschen Anschauungen um (wie erkennt man sie überhaupt?) - und provoziert man sie durch gewisse Veranschaulichungen evtl. sogar?

(Ich bin mir durchaus bewusst, dass die Fragen trotz vorgeblicher Konkretheit teilweise ziemlich abstrakt sind: wie denn z.B. soll ich herausfinden, wie gewisse SchülerInnen Brüche oder Prozente wahrnehmen bzw. welches Vor"wissen" sie haben? Ich kann die Bruch- und Prozentwelt nicht durch die Augen der SchülerInnen sehen, ich kann doch nicht ihre Köpfe aufmeißeln und nachschauen!)

2. Wo ist der günstigste Ort (genauer: die geeignete Unterrichtsphase bzw. das "wann"), um sich mit der Bruch- bzw. Prozentveranschaulichung zu beschäftigen?: vor der Einführung des eigentlichen (mathematisch sauberen) Bruch-/Prozentbegriffs - oder nachher? Ist das beliebig, sprechen für beide möglichen Reihenfolgen gleichgute Gründe - oder gibt es da entscheidende Unterschiede?

3. Welche Veranschaulichungen sind ["warum"] besonders geeignet - und was konkret spricht für kommunizierende Röhren (und gegen sie, "ob")?
   Anders gefragt: sind die kommunizierenden Röhren nur ein (allemal netter!) Gag und eine fixe Idee ohne jeden mathematischen Erkenntnisnährwert?

(... vergleichbar etwa dem Computereinsatz durch Computerfreaks unter den LehrerInneN, die SchülerInnen ihr Privathobby ausbaden lassen.)

Dann wäre es ja doch an der Zeit, dass ein Kollege einen freundlich wieder "auf den Boden herabholen" würde.

Oder sind kommunizierende Röhren umgekehrt (für welche Erkenntnis?) besonders geeignet, wird überhaupt nur (?) an ihnen etwas mathematisch Wichtiges deutlich, bringen nur (?) sie einen erst auf gewisse mathematische Erkenntnisse - und welche?

4. Wenn denn die Entscheidung für kommunizierende Röhren fallen sollte

(sicherlich als eine von vielen Veranschaulichungen, denn genau das ist ja so wichtig:

Ich sehe dich in tausend Bildern,
Maria, lieblich ausgedrückt,
[...]

[Novalis],

d.h. die SchülerInnen sollen ja [relative] Bruchteile in verschiedensten Formen erkennen und vergleichen können):

wie sollen die SchülerInnen damit umgehen? Oder soll ihnen nur ein Kommunizierende-Röhren-Experiment vorgeführt werden

(z.B., weil das entsprechende Gerät a) sehr teuer [und zerbrechlich] und b) deshalb nur einmal vorhanden ist)?

Und selbst wenn das Experiment nur von der Lehrkraft vorgeführt wird: was genau tut sie in welcher Reihenfolge - und was sollen die SchülerInnen (außer stummem "Beobachten") dann tun - und wie "bringt" man sie dazu? Was ist, wenn die SchülerInnen gar nichts [Bedeutsames] erkennen, sondern nur sagen: "da laufen halt Röhren [gleich-]voll, und in China fällt ein Sack Reis um - ja und?" Das ist ja vielleicht sogar erwartbar, weil das Experiment in erster Linie ein physikalisches und nur indirekt ein mathematisches ist.

(Umgekehrt: ist es nicht auch mal eine Chance, dass das Experiment auf Anhieb völlig unmathematisch daherkommt?

[... wobei allerdings - leider! - alles in einer Mathematikstunde von Anfang an unter einem mathematischen Stern steht.]

Und nochmals gewendet: wie kann der mathematische Aspekt dann überhaupt hinzu kommen, ohne dass er von der Lehrkraft aufgepfropft wird?)

Umgekehrt, also wenn die SchülerInnen selbst experimentieren dürfen: wie erreicht man, dass sie nicht (oder nicht die ganze Zeit) einfach nur rumplantschen und den Klassenraum in ein Schwimmbad verwandeln? Ist das sogar als Normalfall erwartbar, wo sie doch endlich mal handgreiflich und "elementar" werden dürfen?

Wie viele Freiheiten der SchülerInnen sind möglich, wie viele Einschränkungen (Anweisungen) sind nötig?

Was an Beobachtungsgabe kann man voraussetzen, wo müssen bzw. können welche (individuellen, teilweisen, differenzierten) Hilfen/Anregungen/Aufgaben gegeben werden - und durch wen?

(... denn das muss ja nicht, wie im Standardunterricht üblich, immer durch die Lehrkraft geschehen!)

Wie genau sollen solche Hilfen/Anregungen/Aufgaben formuliert sein?

(... denn oftmals verstehen SchülerInnen ja nicht mal, was als Hilfe gemeint war

[und dann formuliert man die Hilfe bzw. Frage um und nochmals um und nochmals um ...],

bzw. überhaupt nicht unsere Sprache und Logik;

auch und gerade hier gilt: "vier [Lehrer-]Augen sehen mehr als zwei": bei meinen eigenen Aufgabenstellungen bin ich oftmals betriebsblind, bei denen von KollegInnEn sehe ich aber häufig auf Anhieb, weshalb die Aufgaben nicht funktionieren konnten bzw. funktioniert hatten.)

• Nochmals: wenn denn die Entscheidung für kommunizierende Röhren fallen sollte:

  • (Wie) Werden die kommunizierenden Röhren durch andere (welche?) Modelle ergänzt,

    • seis, dass auf letztere übertragen werden soll,

    • seis, dass die anderen Modelle wichtige Aspekte liefern, die bei den kommunizierenden Röhren nicht auftauchen,

    • seis, dass bei diesen anderen Modellen vielleicht sogar Aspekte auftauchen, die den Ergebnissen bei kommunizierenden Röhren widersprechen oder zu widersprechen scheinen?

  • Was soll wie (ohne Gängelung) aus den Erfahrungen mit kommunizierenden Röhren "allgemeinmathematisch" abstrahiert werden?

• Und selbstverständlich sind noch viele andere (sinnvolle, ergiebige!) Fragen möglich!

ganz wenige Antworten

Ich möchte mich hier (fast) nur mit der Frage beschäftigen:

"Was haben kommunizierende Röhren
im Bruch- bzw. Potenzrechnungsunterricht zu suchen???"

Beginnen möchte ich aber mit dem (oben schon angedeuteten) zumindest vordergründig schlagendsten Argument gegen den Einsatz von kommunizierenden Röhren: entsprechende käuflich zu erwerbende (Fertig-)Modelle sind enorm teuer, und deshalb ist in einigen Schulen vielleicht gar keins vorhanden (oder längst kaputt), und wenn doch, dann höchstens ein einziges. Dieses eine darf aber - gerade weil es so teuer ist - keineswegs in die Hände von SchülerInneN geraten, da es, da aus Glas, sehr zerbrechlich ist.

Es bliebe also überhaupt nur ein Vorführexperiment der Lehrkraft für alle SchülerInnen, d.h. Frontalunterricht.

Nun wären vielleicht simple Modelle nachbaubar, aber da stellt sich doch die Frage, ob a) der Aufwand lohnt und b) die Lehrkraft dafür überhaupt Zeit hat (und wer würde das Material überhaupt bezahlen?).

(Hier läge auch eine Aufgabe für eine Schüler-Modellbaugruppe, seis als eigenständige AG, seis innerhalb des "normalen" Klassen-Unterrichts.

[Allzu oft wird ja übersehen, dass "Selbstlernen" auch "Selbstmachen" heißen könnte!]

Denn beim Bauen [und den sich dabei ergebenden konstruktiven Schwierigkeiten] versteht man oftmals überhaupt erst Grundprinzipien.)

Einen anderen Ausweg könnten hier evtl. Videos bieten (vgl. ), die von EinzelschülerInneN oder Schülergruppen ohne allzu direkte Anleitung durch die Lehrkraft betrachtet werden könnten.

Nun wären solche Videos allerdings (wie so oft) nur Notlösungen: das entscheidend Handgreifliche (und seis das Plantschen) ebenso wie die Selbstbestimmung bei der Versuchsdurchführung würden bei ihnen ja wegfallen.

(Immerhin könnten die SchülerInnen Videos aber "selbstbestimmt" anhalten sowie vor- und zurückspulen.)

Und insbesondere wäre eine Markierung der Gefäße wie z.B. in 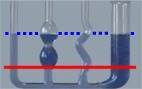  unmöglich.

(Es sei denn, die SchülerInnen zeichnen mit wasserlöslichem Folienstift direkt auf dem [Nicht-Flach-]Bildschirm - oder kleben dazu eine transparente Folie vor den Bildschirm.

Nebenbei: hat das eigentlich jemals jemand vorher bedacht, dass die neuen Flachbildschirme hier einen entscheidenden pädagogische Nachteil haben? Und umgekehrt: hat eigentlich jemals jemand vorher bedacht, dass das Malen auf Bildschirmen eine interessante pädagogische Möglichkeit ist?)

Sinnvoller als das eben angeführte Fertigvideo wäre es also, wenn der Lehrer selbst vom einzig vorhandenen Modell Videos drehen würde, und zwar mal ohne, mal mit Bruch- und Prozentmarken.

Damit aber zur Positivbegründung für

"Was haben kommunizierende Röhren
im Bruch- bzw. Potenzrechnungsunterricht zu suchen???"

Zu allererst wäre

(soweit möglich - und vor aller Bruch- und Prozentrechnung; vgl. )

ein Staunen über den Effekt zu erzeugen, dass das Wasser in allen Röhren immer gleich hoch steht.

Bzw. - schon wieder eine Frage - wie ist der Eindruck zu untergraben, dass das doch ganz selbstverständlich, also langweilig ist?

Zwei Möglichkeiten: 

1. Man fängt mit einem anderen Experiment an: SchülerInnen sollen verschiedenste unverbundene Gefäße 

(aber am besten bereits dieselben wie in )

exakt gleich hoch füllen. Das ist gar nicht so einfach und wird in einem ewigen Nachschütten enden - und evtl. so ähnlich wie das Absägen eines Stuhls, bei dem ein Bein zu kurz ist: man sägt reihum immer weiter, bis gar kein Stuhlbein mehr vorhanden ist.

Nach dieser Vorerfahrung mag es dann wahrhaft erstaunlich scheinen, dass der "Natur" (kommunizierenden Röhren) "mit links" bzw. wie von Zauberhand gelingt, was uns Menschen so enorme Mühe macht.

2. Man führt das Experiment anfangs mit (unterhalb der roten Linie) abgedeckter unterer Querverbindung durch

(... und die SchülerInnen "müssen" sie dann "im Geiste" dazu erfinden bzw. rekonstruieren).

3. Das Modell hat noch immer den Nachteil, dass es zwar einen schönen Effekt zeigt, ansonsten aber nur ein netter Gag, nämlich zu nichts nutze ist. Zu überlegen wäre also

(das möchte ich hier aber nur andenken, ohne dem Gedanken weiter nachzugehen),

wie die staunenswerten Anwendungen des Prinzips kommunizierender Röhren in den Unterricht einbezogen werden könnten

(Wasserleitungen, Wassertürme, "wie leere ich ein Aquarium nur mit einem Schlauch?" ...).

Erst nach wie auch immer erzeugtem Staunen wäre ein langsamer (!) Übergang zur Mathematik angesagt.

Irgendwann käme ja hoffentlich die Frage auf

(wie bringt man die SchülerInnen dazu?),

warum das Wasser in allen Röhren gleich hoch steigt.

Merke: Unterricht muss mehr sein als das, was in vielen modernen Naturkundemuseen vorgeführt wird, nämlich mehr als reine Vorführung der Effekte ohne Frage nach den Ursachen.

Eine erste Begründung anhand einer Grafik

(... wobei ich hier mal weitgehend offen lasse, wie "man" im Unterricht zu diesem vereinfachten Modell käme; vielleicht dadurch, dass die SchülerInnen beim hastigen Auffüllen  kommunizierender Röhren ein sich einpendelndes Hin- und Herschwappen bemerken würden?):

Wenn also die rechte Wassersäule höher stünde als die linke, wäre sie also schwerer und würde die linke hochdrücken, bis Gleichstand vorläge.

Aber trifft diese Erklärung denn immer zu? Was ist denn z.B. im folgenden Fall?:

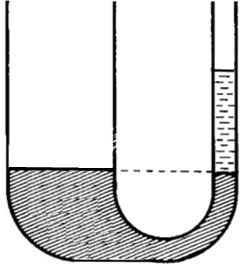
... wenn also der linke Behälter erheblich größer ist als der rechte. Dann ist das Gewicht links doch viel größer als das rechts. Müsste also das Wasser links noch weiter sinken und das rechts noch weiter ansteigen, so dass am Ende (im Gleichgewichtszustand) wahrhaft nicht mehr gleiche Höhe vorläge?

... womit ein fundamentales Prinzip der Physik, nämlich das "hydrostatische Gleichgewicht" [?], eben doch nicht allgemein gälte!?

Nun sieht man aber in der Realität, dass das Wasser in verschieden großen (miteinander verbundenen) Gefäßen dennoch immer auf gleiche Höhe steigt:

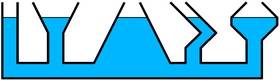
An der (allemal naheliegenden!) Erklärung mit den verschieden großen Gewichten der Wassersäulen ist also irgendwas faul.

Nun weiß ich selbst nicht die korrekte Antwort

(oder ahne sie nur: es liegt nicht am Gewicht der Wassersäulen, sondern am Luftdruck?; aber wie genau?).

Vielmehr wird man durch das Problem auf den eigentlich interessanten Aspekt aufmerksam:

• negativ formuliert: dass das Wasser in gleichen Säulen auf gleiche Höhen steigt, ist "trivial";

• positiv formuliert: interessant wirds also erst, wenn die Säulen verschieden groß sind

(völlig verschiedene Formen seien hier vorerst ignoriert; aber darauf wird - s.u. - zurückzukommen sein):

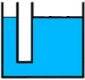
Und hier nun wirds überhaupt mathematisch (im Hinblick auf Bruch- und Prozentrechnung) interessant: bei beiden Behältern (links und rechts) ist

• die Füllhöhe gleich (sie sind beide zu ca. 70 % der Gesamthöhe gefüllt),

• aber die Füllmenge links offensichtlich erheblich kleiner als die rechts.

(es sei allerdings ergänzt:

• links sind 70 % der möglichen Gesamtfüllmenge erreicht [einer kleinen Gesamtfüllmenge),

• rechts sind ebenfalls 70 % der möglichen Gesamtfüllmenge erreicht [einer großen Gesamtfüllmenge].

Durchaus hilfreich ist - nebenbei - auch, dass das gefärbte [!] Wasser in breiteren Gefäßen bzw. an breiteren Stellen dunkler wirkt:

Selbst die Wasserfarbe kann also pädagogisch bedeutsam sein!)

Weil

• nur die Füllhöhe wichtig ist,

• aber weder Gefäßgröße noch (s.u.) -form,

gilt:

Ich bin immer "verzweifelt" auf der Suche nach anschaulichen "Grundmetaphern der Mathematik"

(beispielsweise ist eine Balkenwaage, die in stetigem Gleichgewicht gehalten werden muss, die Grundmetapher für eine Gleichung[sumformung]).

SchülerInnen brauchen dringend solche Grundmetaphern

(bei denen dringend überlegt werden muss, ob sie die Erkenntnis nicht auch irreleiten können!; vgl. unten "Grenzen des Modells"),

und zwar zumindest solange (und darüber hinaus?), bis Rechnungen bei ihnen vollautomatisch (ohne Anschauung) ablaufen.

besagt nichts anderes, als dass (bei Gefäßen gleicher Form) der Bruch-/prozentuale Anteil

• nur von der Höhe,
• nicht aber von der Breite abhängt

(weil hier nur zweidimensionale Darstellungen vorliegen, sei hier die Tiefe vernachlässigt):

Ein Whiskey-Glas ist

• für einen Optimisten halb voll,

• für einen Pessimisten halb leer

völlig unabhängig davon, wie breit es ist:

Wenn

• völlig identische Behälter, also

,

logisch gesehen der 1. (und völlig witzlose) Schritt und

•  unterschiedlich große Behälter gleicher Form, also

,

 der 2. Schritt sind,

so sind

• verschiedenförmige Behälter konstant gleicher Breite (bzgl. jeweils desselben Behälters) der 3. Schritt:

• und verschiedenförmige Behälter mit teilweise zu- und abnehmender Breite der 4. Schritt:

äUSSERST WICHTIG: die oben behandelte Gleichheit bzgl. der Gesamtfüllmengen gilt NICHT bei Gefäßen, die sich verjüngen bzw. erweitern. Hier liegen die GRENZEN DES MODELLS - und umgekehrt auch der von ihm provozierte  Erkenntnisgewinn!

Vgl. dazu :

• in beiden Behältern ist jeweils die Hälfte der Füllhöhe erreicht,

• im linken Behälter ist auch die Hälfte seiner Gesamtfüllmenge erreicht,

• im rechten Behälter ist wegen der Verdickungen unten bereits weit mehr als die Hälfte seiner Gesamtfüllmenge erreicht.

Klassischer Unterricht würde immer in genau dieser vorgekauten logischen Reihenfolge vorgehen.

(SchülerInnen werden da wahrgenommen wie Neckermann-Pauschalreisende, die permanent ans Händchen genommen werden müssen.)

Ich hingegen frage mich

(ohne dass ich das hier ausführen möchte),

inwieweit man (einige/alle) SchülerInnen direkt an

setzen kann/darf/sollte und ob sie daraus die "Grundproblematik" selbst rausfinden können.

PS:	In dem Film läuft das Wasser im schrägen Behältnis schräg hoch: Preisfrage: warum? Liegt das an der "Adhäsion"?