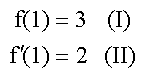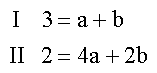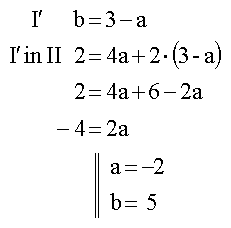Eine unbekannte Funktion hat die Gleichung Sie verläuft durch den Punkt P(1;3) und hat dort die Steigung 2. Wie lautet die Funktionsgleichung ?
1.	Die allgemeine Gleichung der gesuchten Funktion ist schon gegeben. Ihre Ableitung lautet : Eine zweite Ableitung wird nicht benötigt, da keine Aussagen über die Krümmung gemacht wurden.
2.	Die bekannten Merkmale sollte man wie folgt notieren :
3.	Durch Einsetzen in f(x) und f'(x) erhält man das Gleichungssystem welches nun z.B. mit dem Einsetzungsverfahren zu lösen ist.
4.	Mein Lösungsvorschlag sieht so aus :
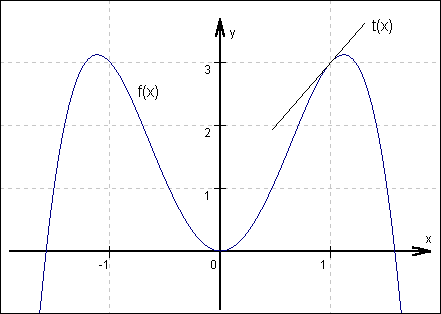
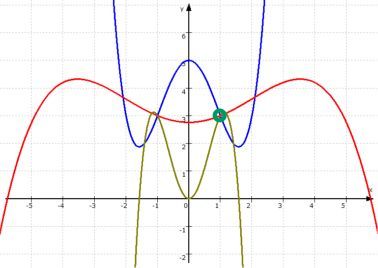
5.	Somit lautet die gesuchte Funktionsgleichung : Der Anschaulichkeit wegen hier noch das Bild : Wie verlangt verläuft f(x) durch den Punkt (1;3), die richtige Steigung kann an der Tangente t(x) abgelesen werden.

---

Was soll solch eine Aufgabe?:

• bei der üblichen "Kurvendiskussion" wird genau umgekehrt zur eben zitierten Aufgabe verfahren: man hat vorweg eine Funktionsgleichung

(eben z.B. )

und soll deren mehr oder minder markante Eigenschaften herausfinden

(z.B. "Sie verläuft durch den Punkt P(1;3) und hat dort die Steigung 2").

Üblicherweise ist es also das Ziel von Kurvendiskussionen, zu arg abstrakten algebraischen Funktionsgleichungen geometrisch-anschauliche Vorstellungen, also die Funktionsgraphen, zu finden: 

	Funktionsgleichung	→	markante Eigenschaften / Funktionsgraph
	Algebra	→	Geometrie

• Die o.g. Aufgabe ist ein klassisches Beispiel für das umgekehrte Vorgehen:

zu gewissen geometrisch-anschaulichen Vorgaben

(z.B. "Sie verläuft durch den Punkt P(1;3) und hat dort die Steigung 2")

wird umständlich die ursprüngliche algebraische Funktionsgleichung

(z.B.  )

rekonstruiert bzw. überhaupt erst ermittelt:

	Funktionsgleichung	←	markante Eigenschaften / Funktionsgraph
	Algebra	←	Geometrie

Mathematiker halten beide (rein innermathematischen) "Richtungen", also → und ← , für wichtig, wobei ← wohl eher in Anwendungsaufgaben vorkommt, wo oftmals zu gewissen Daten überhaupt erst (halbwegs) passende Funktionen (Funktionsgleichungen) gesucht werden.

---

"Witzig" ist an all dem

(wie an der  gesamten Mathematik!)

natürlich gar nichts

(man kann mit Mathematik jedoch immerhin witzig - und selbstironisch -   umgehen).

Und somit mache ich es auch dem Autor der o.g. Aufgabe nicht zum Vorwurf, dass die Aufgabe nicht witzig ist: er wollte doch wohl nur an einem einfachen (?) Beispiel vorführen, wie die "umgekehrte Kurvendiskussion" rechnerisch funktioniert.

Wenn eine Sache allerdings "nicht witzig" ist, folgt scheinbar automatisch, dass sie "witz-los" ist.

Nun ist aber erstaunlicherweise

• "witzlos" keineswegs das Gegenteil von           "witzig" und also

• "witzlos" keineswegs ein Synonym   von "nicht witzig".

Vielmehr bedeutet

1. (nicht) "witzig", dass (k)eine - nennen wir's mal so - humorvolle Geschichte vorliegt

(z.B.

Zwei Ballonfahrer fahren nebeneinander im Nebel. Ruft der eine zum anderen rüber: "Wo sind wir?" Der andere denkt zwei Stunden nach und antwortet dann: "Im Ballon!"

Welchen Beruf hat der zweite?

Mathematiker!, denn die Antwort

1. hat ewig auf sich warten lassen,
2. ist absolut exakt und
3. völlig unnütz!) ,

2. "witzlos" hingegen , dass "an der Sache kein Witz ist"

(vgl. "der Witz an der Sache ist ...").

Hier ist mit "Witz" allerdings

1. nicht mehr eine humorvolle Geschichte, sondern

2. ein Geistesblitz

gemeint

(vgl. "er ist  gewitzt"', d.h. "er ist [so definiert arg schlapp der Duden:] schlau").

"Witz: Das Substantiv [...] bedeutete ursprünglich Wissen, woraus sich die Bedeutung »Verstand, Klugheit, Schlauheit« entwickelte. Im 17. Jh. kam im Dt. die Verwendung im Sinne von »Esprit, Gabe des geistreichen Formulierens« unter dem Einfluß von frz. esprit »Geist, Witz« und engl. wit »Geist, Witz« auf. Die Bedeutung »Spott, Scherz; scherzhafte Äußerung« erscheint seit dem 18. Jh."

Erstaunlicherweise ist also die Bedeutung b. älter als die Bedeutung a. - und vielleicht ist das eben doch gar nicht so erstaunlich: Schlauheit ist eben die Voraussetzung für gute Witze, bzw. das beste Kriterium für Intelligenz ist noch immer Humor (inkl. Selbstironie).

---

Die o.g. Aufgabe kann zwar gar nicht "witzig" sein, aber deshalb muss sie noch lange nicht so "witz-los" sein, wie sie daher kommt.

Was  also könnte der (zu ergänzende) "Witz" an der o.g. Aufgabe sein? Bzw. "Witz, komm' raus, du bist umzingelt".

---

Als ich die o.g. Aufgabe mit einer Klasse durchnahm und dazu erstmal vorlas, stutzte eine Schülerin bereits nach dem ersten Teilsatz

"Eine unbekannte Funktion hat die Gleichung [...]"

merklich und wies dann auf den Widerspruch hin, dass

• die Funktion einerseits angeblich unbekannt ist,

• anderseits aber im Folgenden dann doch ihre Funktionsgleichung genannt wird.

"Eine unbekannte Funktion hat die Gleichung [...]" ist also anscheinend - gelinde gesagt  - ungünstig formuliert. Fragt sich nur, was eine bessere Alternative wäre.

Nun könnte man natürlich einfach das Adjektiv "unbekannte" weglassen, womit man

• "Eine Funktion hat die Gleichung   [...]" bzw.

• "Eine Funktion hat die Gleichung [...]"

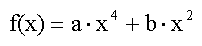erhalten würde. Aber diese gekürzte Formulierung ist keineswegs besser, da ja

• nicht die Gleichung einer einzigen (nämlich der gesuchten) Funktion, sondern

• einer ganzen Funktionenschar

(mit unendlich vielen Familienmitglieder; vgl. engl. "function family")

ist, in der die gesuchte Funktion f nur eines der unendlich vielen Familienmitglieder ist.

Korrekt wäre da hingegen der Satzanfang "Gesucht ist diejenige Funktion f aus der Funktionenschar , die [...]"

(... wobei es allerdings wohl besser f_ab hieße).

Der Satzanfang "Eine unbekannte Funktion hat die Gleichung [...]" ist aber überhaupt nur so verwirrend und (scheinbar!) widersprüchlich, weil man fest damit rechnet, dass eine exakte Funktionsgleichung

(nämlich z.B. f: y = - 2x⁴ + 5x² )

folgt

(was allerdings vollends witzlos wäre, da dann ja bereits alles gleich am Anfang verraten wäre und nichts mehr zu tun bliebe).

Nun wird aber die soeben erzeugte Erwartung, dass die exakte Funktionsgleichung folgen wird, mit umgehend enttäuscht, da mit ja eine Funktionenschar aus unendlich vielen Einzelfunktionen folgt. Immerhin wird aber die "Familie", aus der f stammt, schon erheblich eingeschränkt:

1. von allen (unendlich vielen!) möglichen Funktionen und Funktionsarten

bleiben

2. wegen ax⁴ + bx² nur die (ihrerseits immer noch unendlich vielen) ganzrationalen Funktionen übrig:

3. bleiben davon wegen des höchsten Exponenten 4 nur die ganzrationalen Funktionen vierten Grades übrig, was allerdings auch immer noch unendlich viele sind:

4. bleiben davon, da nur die geraden Exponenten 4 und 2 und somit nur sogenante "biquadratische" Funktionen auftauchen, nur die (immer noch unendlich vielen) zur y-Achse symmetrischen übrig:

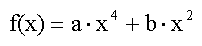
5. bleiben davon, weil in  das sogenannte "absolute Glied" null ist, nur diejenigen Funktionen übrig, die durch den Ursprung gehen - was (gähn!) immer noch unendlich viele sind:

Da aber trotz vierfacher Einschränkung (b. - e.) noch immer unendlich viele Funktionen möglich sind, ist die Funktionsdefinition mit der Funktionenschargleichung noch gar nicht abgeschlossen, sondern folgen in der Aufgabe noch zwei weitere (mehr oder minder sinnige) Einschränkungen:

6. "Sie [die gesuchte Funktion] verläuft durch den Punkt P (1;3) ", d.h. von den (immer noch) unendlich vielen Funktionen aus e. bleiben nur diejenigen mit dieser "Punkt-Eigenschaft" übrig, was allerdings (man erwartet es inzwischen gar nicht mehr anders) auch immer noch unendlich viele Funktionen sind:

7. "[die gesuchte Funktion] hat dort [= im Punkt P (1;3)] die Steigung 2"; zumindest ich sehe da nicht auf Anhieb, wie viele Funktionen jetzt noch übrig bleiben: wieder unendlich viele, mehrere, eine - oder vielleicht auch gar keine?

(Nur die Logik der Aufgabe besagt, dass am Ende eine einzige, nämlich die gesuchte Funktion herauskommt: "Witz, komm' raus, du bist [durch die Einschränkungen b. - g.] umzingelt!")

Insbesondere bleibt trotz sechsfachen, immer feineren Siebens

unklar, welche konkrete Funktion (nämlich  ) sll die zunehmenden Einschränkungen erfüllt.

Die gesuchte Funktion bleibt also vorerst - wie anfangs gesagt - unbekannt.

Bei der Entscheidung,

1. wie viele Funktionen am Ende übrig bleiben bzw.

2. welche konkrete (einzige) Funktion das ist,

hilft aber nur noch das algebraische Rechnen, das der Autor der Aufgabe vorgeführt hat. Erst dieses Rechnen ist abstrakt - und natürlich ist es wichtig, da die Entscheidungen 1. und 2. anderweitig ja gar nicht getroffen werden können.

Dennoch ist das Rechnen doch nur ein witzloser Wurmfortsatz der von mir oben angestellten Einschränkungs-Geschichte.

"Witzig" ist vielmehr

1. , dass wir in den Schritten a. - f.

• jeweils von unendlich vielen Funktionen (∞₁)

• unendlich viele (∞₂) wegnehmen - und dennoch

• jeweils noch unendlich viele (∞₃) übrig bleiben:

∞₁ - ∞₂ =∞₃,
wobei allerdings gleichzeitig ∞₃ sehr viel weniger  als ∞₁ ist, also
∞₁ > ∞₃.

2. im Schritt g. (wie allerdings erst die Rechnung zeigt) nach all den (wenn auch paradoxerweise immer kleiner werdenden) ewigen Unendlichkeiten urplötzlich doch (dann endlich!) nur noch eine einzige Funktion, nämlich 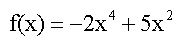, übrig bleibt.

Es ist, als wenn wenn

• eine unüberschaubar große Herde Rinder von Cowboys immer weiter eingekreist wird,

• dabei immer  mehr Rinder außen vor bleiben - und urplötzlich

• nur noch ein einziges Rind mit dem Lasso herausgefangen wird

(ganz nebenbei gesagt und dennoch bemerkenswert: solch "unsachliche" und doch, wie mir scheint, enorm wichtige Vergleiche tauchen niemals in "richtiger" Mathematik auf, sondern sind meine eigentliche Spezialität).

Oder es ist wie der "Wahrscheinlichkeitskollaps" in der Wahrscheinlichkeitsrechnung, bei dem

• aus vielen Möglichkeiten (beim Würfel 1, 2, 3, 4, 5, 6)

• urplötzlich (wenn der Würfel zum letzten mal kippt) eine Sicherheit wird (z.B. die 4 oben liegt), d.h. alle Möglichkeiten urplötzlich verschwinden bzw. zu einer einzigen Sicherheit gefrieren (schockfrosten) oder versteinern.

---

Nun wollen wir (?) aber nicht pauschal den Rechnungen Unrecht tun, die durchaus auch "witzig" sein können, wenn sie überraschende Wendungen nehmen, nämlich

• urplötzlich auf den Punkt kommen

(was oftmals aus der mathematischen Logik folgt, also ohne Zutun eines Menschen, und dann fast die Mathematik selbst intelligent oder das Ergebnis als Gottesgabe/Musenkuss erscheinen lässt)

oder 

• ungewohnte Wege gehen

(neue Rechenverfahren oder eine neuartige Kombination bislang unverbundener mathematischer Sachverhalte).

Nun ist aber die Rechnung zu unserer hier behandelten Aufgabe derart konventionell, dass sie einem kaum mehr "witzig" erscheinen kann.

Wer ist hier "einem"?: oftmals wohl die MathelehrerInnen, die solche Aufgaben derart häufig durchgenommen haben, dass sie gar nicht (mehr) deren Gags erkennen können (und daher eigentlich durchaus Interessantes nur noch langweilig vermitteln; vgl. den Deutschlehrer, der zum hundersten Mal den "Faust" durchnimmt und dem dabei nicht die mindeste persönliche Begeisterung [mehr] anzumerken ist, sondern der mangels eigener [nie vorhandener?] Begeisterung nur die Konvention totreitet, dass der "Faust" der Olymp der gesamten deutschen Literatur sei), die Schwierigkeiten verstehen (antizipieren) können, die viele SchülerInnen damit haben.

	Geometrie		Algebra
	Der Funktionsgraph von f(x) = ax4 + bx2 hat im Punkt P ( 1 ; 3 ) die Steigung 2	⇔	1 und 2 erfüllen die  Funktonsgleichung der Ableitung, also von           f  ' (x) = 4a   x3 + 2b   x  . d.h.            2    = 4a • 13 + 2b • 1                ⇔  2    = 4a         + 2b            (der y-Wert 3  des Punktes  ( 1 ; 3 ) spielt hier - nebenbei gesagt - keine Rolle mehr)

Mit a. und b. haben wir es nun aber endlich geschafft, die beiden geometrischen Zusatzinformationen

1. die Funktion geht durch den Punkt P ( 1 ; 3 ),

2. sie hat in P ( 1 ; 3 ) die Steigung 2

der Aufgabe in die benötigten beiden algebraischen Zusatzgleichungen

1.                 3 =   a         +   b  ,

2.                 2 = 4a         + 2b

zu übersetzen.

Und damit haben wir das Gleichungssystem

3 =   a         +   b    I.  2 = 4a         + 2b    II.

• aus den zwei Gleichungen I. und II.

• mit  den zwei Unbekannten a und b.

Wenn es denn überhaupt Lösungen für a und b gibt, so müssten sie nun sehr einfach (?) zu berechnen sein.

---

Uff, das ist geschafft! - und jetzt nehmen wir uns Zeit zum Innehalten: • Der "Witz" der Mathematik besteht vielleicht darin, dass es auch in ihr - eine Dramatik bzw. Spannungs- oder Fieberkurven - Crescendi und Decrescendi, - Beschleunigung und Abbremsen, - Spannung und Entspannung, - Langeweile und Routine, - Verzweiflung und unbändige Freude gibt: Rechnungen bzw. Beweise entwickeln sich nicht langweilig stetig und linear, also z.B. so oder gar so  ,   sondern mit abrupten Sprüngen und wilden Ausschlägen: Nur ist es leider üblich, all das in mathematischen Texten zu löschen, und entsprechend plätschert wohl auch der meiste Matheunterricht ewig gleichmäßig dahin. Wegen all dem bin ich - zumindest im Hinblick auf Schulen - noch immer ein großer Anhänger des guten alten mathematischen Aufsatzes, in dem immerhin - wie in jedem guten Text - nach Sinneinheiten (Erreichen von Zwischenzielen) Absätze gemacht werden sollten. • Insbesondere wird mir zu wenig im Matheunterricht gefeiert, wenn man wichtige Zwischenziele erreicht und endlich wieder halbwegs festen Boden unter den Füßen hat        (vgl.   ). Ohne solches Feiern des Erreichens von Zwischenzielen kommen einem nämlich die Zwischenziele selbst abhanden und erscheint einem die ganze Mathematik wie ein strukturloser Nebel, in dem man ziellos herumstochert. • Im selben Augenblick, in dem wir das Gleichungssystem haben, verlassen wir die Oberstufenmathematik (Analysis) und befinden wir uns wieder im sicheren (?) Hafen der Mittelstufenmathematik (Algebra). Man muss hier nämlich im Hinblick auf Schülerleistungen deutlich differenzieren: - die einen haben Schwierigkeiten mit dem Neuen (der Analysis): ihnen fehlen das "Grundgesetz" und insbesondere seine Abwandlung für die erste Ableitung, - bei den anderen rächen sich in alle Ewigkeit uralte Versäumnisse (hier das algebraische Lösen von Gleichungssystemen). Ist das gleich "schlimm", d.h. ist "falsch" = "falsch"?   (Man neigt als Lehrer beim Korrigieren dazu, gar nicht mehr mitzubekommen, woran's denn eigentlich hapert, und deswegen können SchülerInnen auch kaum mal ihre individuellen Probleme ["meine Lieblingsfehler"] angehen.) • (Erst) in dem Augenblick, in dem wir die Analysis verlassen und beim algebraischen Lösen eines Gleichungssystems sind, erreichen wir (das kann man ja auch mal positiv sehen:) den sicheren Hafen der reinen Mathematik: dem Gleichungssystem    3 =   a         +   b    I.  2 = 4a         + 2b    II. ist nicht mehr im mindesten anzusehen, aus welchem Kontext (Suche nach einer bestimmten Funktion) es stammt.