Cantor noch anschaulicher

Dieser Aufsatz ist "nur" ein "kleiner" Nachgedanke zu  

Die natürlichen Zahlen 1, 2, 3, 4 ... kann man hübsch nacheinander, also eindimensional anordnen wie

• eine Inselkette

Während also die natürlichen Zahlen alle hübsch brav und überschaubar hintereinander liegen, kann man solch eine Ordnung bei den Brüchen auf den ersten Blick nicht erkennen. Sie liegen zwar auch alle auf dem (eindimensionalen) "Zahlenstrahl", aber doch leider völlig chaotisch. So ist etwa die Größenordnung von Brüchen bzw. ihr Verhältnis zueinander kaum zu erkennen. Beispielsweise gilt  , obwohl doch 10 > 9 < 16 und 5 > 3 < 4 ist.

Nun haben Brüche aber immerhin den Vorteil, dass sowohl ihre Zähler als auch ihre Nenner natürliche (bzw. ganze) Zahlen sind. Und immerhin kann man die Beziehung zwischen zwei Brüchen in zwei Spezialfällen gut erkennen:

1.           wenn sie "gleichnamig" sind, also denselben Nenner haben:

Für die Brüche mit dem Nenner 1, also für , erhalten wir somit dasselbe (horizontale) Nacheinander wie bei den natürlichen Zahlen:

In genau derselben Art lassen sich nun aber die Brüche mit dem gemeinsamen Nenner 2 (und 3, 4, 5 ...) anordnen:

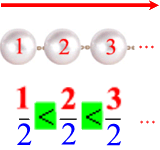
(Und wieder: es gibt offensichtlich genauso viele Brüche mit dem Nenner 2 [oder 3, 4, 5 ...], wie es natürliche Zahlen gibt.)

All unsere "Bruchreihen", also ,  usw. können wir nun aber untereinander anordnen:

Und hier nun kann man feststellen, dass man auch vertikal wie bei den natürlichen Zahlen zählen kann:

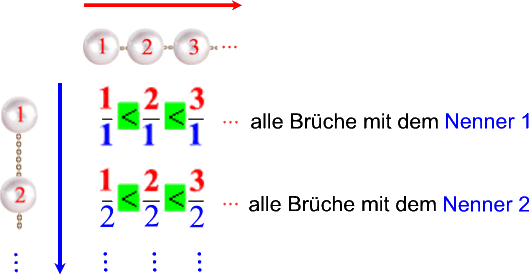
Es gibt also auch genauso viele Zeilen wie natürliche Zahlen.

Halten wir also für unser Schema fest:

Die Kombination aus a. und b. ergibt aber: es gibt in unserem Schema insgesamt

(Anzahl der natürlichen Zahlen) mal (Anzahl der natürlichen Zahlen)

Brüche.

Wir tun hier hier natürlich etwas sehr Seltsames bzw. Zweifelhaftes, denn immerhin ist die Anzahl der natürlichen Zahlen ja unendlich, d.h. wir rechnen

unendlich mal unendlich = ???

Um aber unser bisher erstelltes Schema noch anschaulicher zu machen, sortieren wir die Brüche auf die soeben dargestellte Weise in ein Regal durch sukzessive Ergänzung neuer Regalbretter untereinander ein:

2. Genauso gut könnten wir auch alle Brüche mit demselben Zähler betrachten und sie diesmal vertikal anordnen. Wir würden dann durch sukzessives Hinzufügen schmaler Regale nebeneinander erhalten:

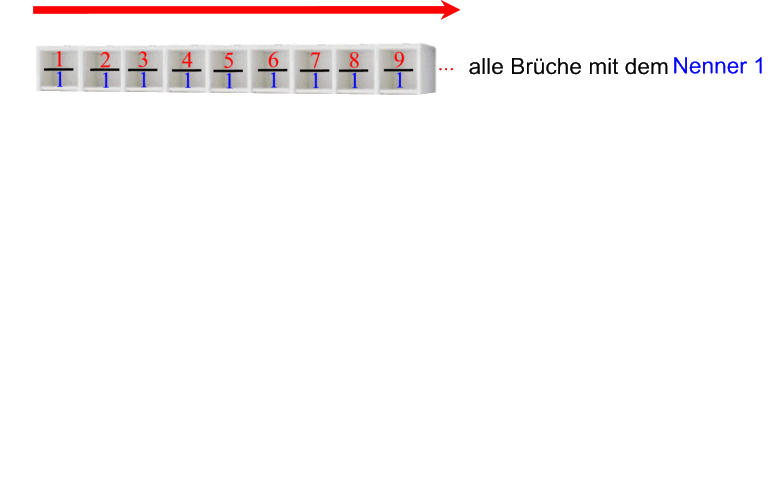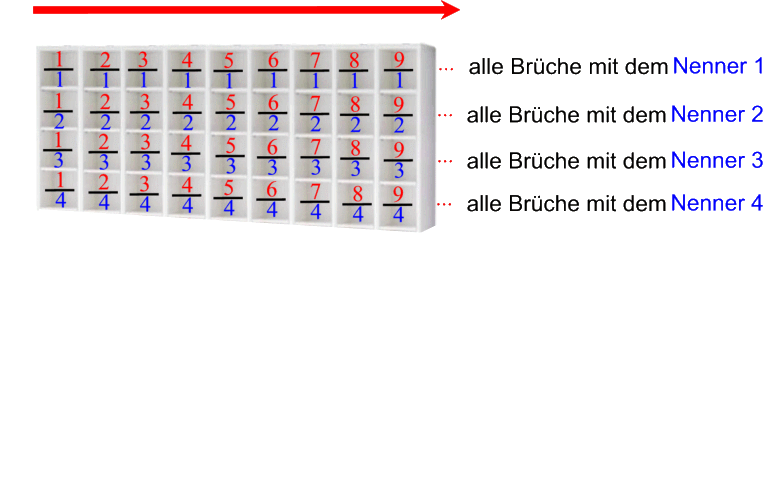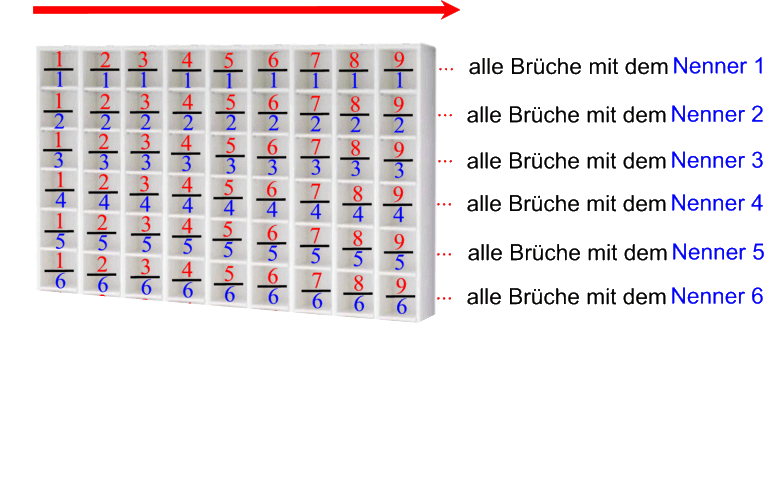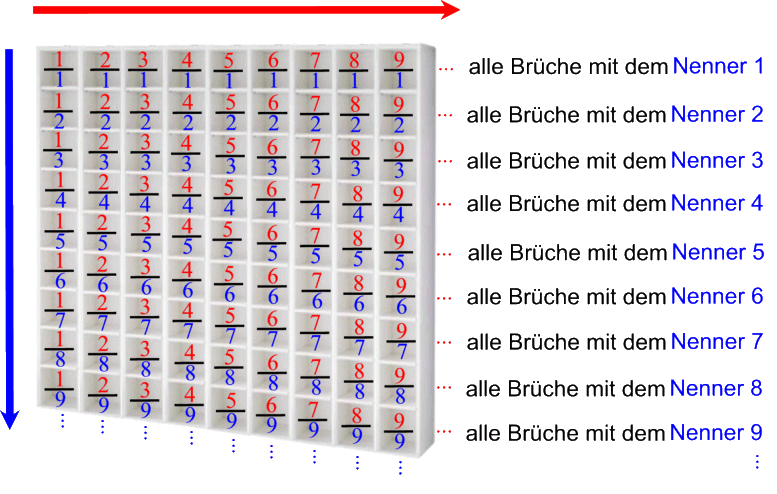
1. und 2. ergeben also dasselbe Schema, das vollständig so aussieht:

Vergewissern wir uns zu allererst, dass darin auch tatsächlich alle Brüche vorkommen. Dazu machen wir uns klar, dass das Regal zweidimensional ist, also beispielsweise die Position des Bruchs durch die beiden Koordinaten

• 7 (7. Spalte),
• 3 (3. Zeile)

bestimmt ist:

Und genauso kommt nun auch jeder andere Bruch in dem (nach rechts und unten fortgesetzten) Regal vor, also beispielsweise in der

• 539. Spalte,
• 274. Zeile.

Nun wissen wir ja, dass die natürlichen Zahlen eine echte Teilmenge der Brüche sind (weil z.B. ), und all diese natürlichen Zahlen kommen in der Tat in unserem Regal vor, und zwar schon in der 1. Zeile! Genauso kommen aber auch viele nicht-natürliche Zahlen, also echte Brüche in unserem Regal vor, nämlich eben z.B.   (s.o.).

Des Weiteren ist bemerkenswert, dass alle Brüche mehrfach (sogar unendlich oft!) in unserem Regal vorkommen, nämlich z.B. alle (unendlich viele!) Erweiterungen von :

Das soll uns aber - wie unten noch erklärt wird - nicht weiter stören: besser zu viele als zu wenige!

Leider ist das Regal aber noch immer zweidimensional. Cantors geniale Idee bestand nun aber darin, es eindimensional zu machen, ohne dabei aber irgendwelche Brüche zu verlieren.

Ziel ist also solch ein Regal aus nur einer einzigen Zeile bzw. einem einzigen Regalbrett:

oder aber

Beim Versuch, das zweidimensionale Regal eindimensional zu machen, ist es allzu verführerisch, mit einer (ganzen) Zeile oder Spalte anzufangen. Weil jede solche Zeile oder Spalte aber unendlich lang ist, hieße das, dass wir nie aus ihr heraus kämen

 (also schon allein nicht zur zweiten Zeile/Spalte, geschweige denn zu den folgenden Zeilen/Spalten).

Oder anders gesagt:

• wir dürfen nicht
  • nur ganze Zeilen oder
  • nur ganze Spalten

verwenden, sondern müssen (schade!) das Gesamtregal bzw. die Regalzeilen und -spalten in seine/ihre Einzelzellen zersägen:

• wir müssen zwischen Zeilen und Spalten wechseln.

Gesucht ist also ein "Weg", der

• ab und zu zwischen Zeilen und Spalten wechselt,
• systematisch verläuft, so dass er, obwohl wir natürlich nur seinen Anfang zeichnen können, in alle Ewigkeit so weiter gedacht werden kann.

Um nun aber das schöne Regal nicht kaputt zu machen, legen wir eine eindimensionale durchgehende () Perlenkette durch dieses Regal, und zwar pro Regalfach eine Perle. Nur darf diese Perlenkette nicht so hübsch "ausgestreckt" hintereinander verlegt, sondern muss vielfach gebogen werden.

Es gibt mehrere gesuchte eindimensionale (und systematische!) Perlenkettenwege durch das Regal, aber fangen wir zaghaft mit einem der möglichen Wege an - und beginnen, um wirklich alle Brüche zu erwischen, oben links in der Ecke mit , von wo wir

(noch haben wir die freie Wahl)

einen Schritt nach rechts zu gehen:

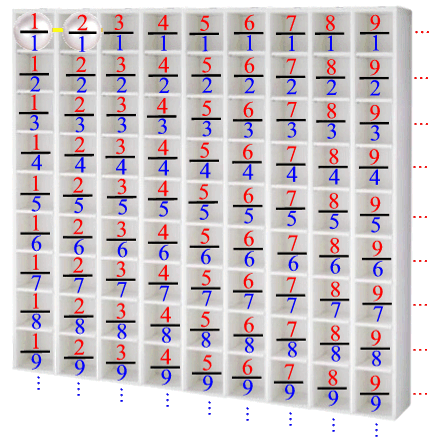
Eingedenk unseres Vorhabens, Zeilen und Spalten zu wechseln, und um am Anfang der zweiten Zeile nicht zu vergessen, gehen wir dorthin, indem wir jetzt gleichzeitig eine Zeile tiefer und eine Spalte rückwärts, also diagonal nach schräg links unten gehen:

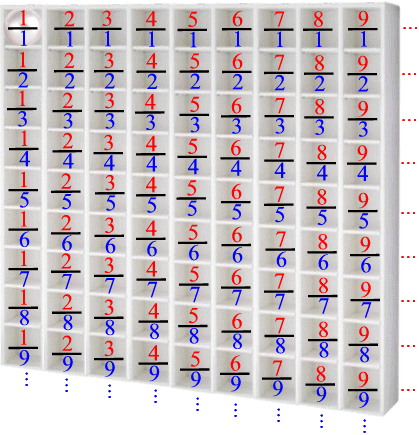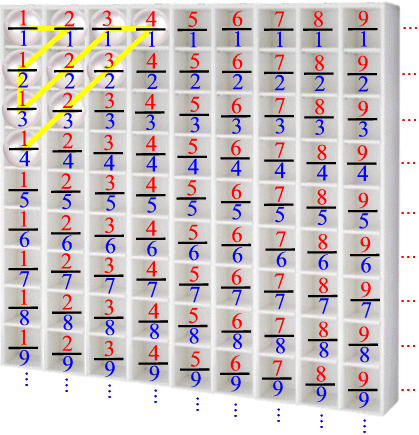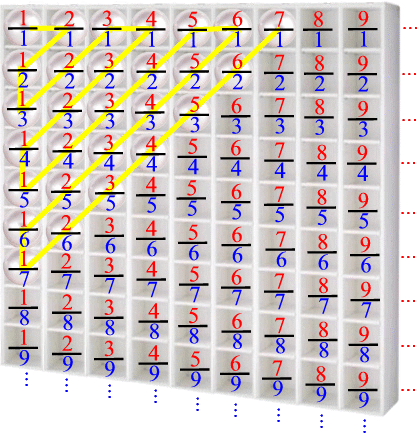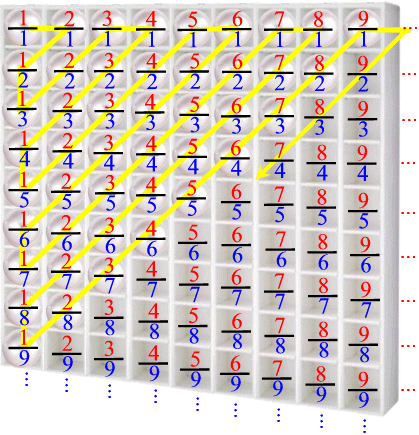
Wir haben damit eine vollständige Diagonale benutzt, und um systematisch bei dieser Idee zu bleiben, gehen wir erstmal nach unten zu und dann wieder (parallel zu ersten Diagonale) schräg nach rechts oben:

(Wohlgemerkt: solche Diagonalen müssen immer von links unten nach rechts oben bzw. umgekehrt verlaufen, da sie dann endlich sind. Diagonalen hingegen, die von links oben nach rechts unten oder umgekehrt liefen, wären unendlich lang und wir kämen nie wieder aus ihnen raus und könnten somit nie den Rest erledigen.)

Mit dem - so wird es seit Cantor genannt - "Diagonalenverfahren" ist aber schon das vollständige System angedeutet, das dann so weitergeht:

Nun lassen wir noch das Regal weg und erhalten:

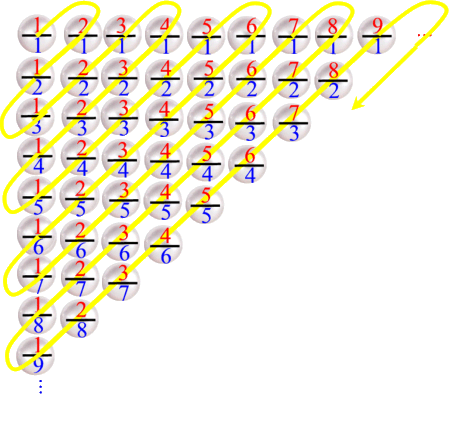
Diese Perlenkette lässt sich nun aber wieder "gerade" biegen, und dann erhalten wir zwar ein wenig durcheinander

(d.h. auch: nicht [mehr] der Größe nach sortiert, also nicht in der Reihenfolge wie auf dem Zahlenstrahl),

aber eben doch endlich hintereinander

.

Damit aber haben wir endlich alle (!) Brüche anschaulich eindimensional hintereinander angeordnet.

Schön und gut, aber was "haben" wir davon bzw. wo ist der "Witz" des Ganzen?

Erinnern wir uns dazu, dass wir die natürlichen Zahlen genauso auf einer Perlenkette anordnen konnten.

Wenn wir nun diese beiden Ketten parallel anordnen, erhalten wir 

Also kann jeder natürlichen Zahl ein Bruch und umgekehrt jedem Bruch eine natürliche Zahl zugeordnet werden:

Das aber bedeutet:

(Und da man die natürlichen Zahlen abzählen kann

[nämlich "eins, zwei, drei ..."],

sagt man, dass somit auch die Brüche "abzählbar" sind:

)

Man muss aber den "süßsauren" Beigeschmack des Satzes

bemerken:

1. "sauer": er widerspricht doch rundweg unserem (auch oben gezeigten) sicheren (!) Wissen, dass die natürlichen Zahlen eine ECHTE TEILmenge der Brüche sind, dass es also ganz eindeutig erheblich MEHR Brüche als natürliche Zahlen gibt; Cantors Beweis muss - so gesehen - wie ein übler Taschenspielertrick wirken, bei dem es zwar mit rechten Dingen zugeht (der mathematisch richtig ist), der einen aber eben doch überrumpelt bzw. reinlegt

(wohlgemerkt: es ist nicht Cantor, der uns da reinlegt [eine mathematische Wahrheit ist unabhängig von ihrem Erfinder/Entdecker], sondern die Logik selbst); 

2. "süß": gleichzeitig ist aber der Beweis, dass es GLEICH VIELE Brüche wie natürliche Zahlen gibt, "wasserdicht" und von genialer (im Nachhinein: genial einfacher) Eleganz.

Wir wissen also, wie so einige Mal in der Mathematik oder auch in den Naturwissenschaften, zwei Sachen gleichzeitig (und beide absolut sicher), die sich aber schlicht gegenseitig widersprechen.

Ich habe aber was dagegen, solche Widersprüche leichtfertig zu einer der beiden Seiten hin aufzulösen, und zwar immer

• zu Ungunsten der (als falsch denunzierten) Anschauung (hier, dass es offensichtlich mehr Brüche als natürliche Zahlen gibt)
• und zu Gunsten der mathematischen Wahrheit (hier Cantors Beweis)

(vgl. ).

Ja, ich glaube sogar, dass insbesondere die großen Genies sich an solchen Widersprüche gerieben, sich an ihnen abgearbeitet und oftmals überhaupt erst dadurch zu neuen Erkenntnissen gekommen sind.

Die Entschärfung des Widerspruchs (und die Beseitigung des Staunens) ist zudem historisch unredlich: immerhin ist Cantor wegen seiner Erkenntnisse zur Unendlichkeit von vielen "großen" Mathematikern seiner Zeit fertig gemacht, ja regelrecht in den Wahnsinn getrieben worden. Was ja nicht nur zeigt, wie gemein auch Mathematiker sein können, sondern diese anderen "großen" Mathematiker haben eben auch ihre lieben Schwierigkeiten mit Cantors Erkenntnissen gehabt, die nunmal gehirnausrenkend waren - und bleiben.

(ärmlich sind jene Leute, die meinen, nur unsere Vorfahren seien noch dumm gewesen, wir aber seien der Höhe- und Endpunkt des Universums: )

Wohlgemerkt: ich habe etwas dagegen, Widersprüche "leichtfertig" aufzulösen. Denn versuchen sollte man es natürlich dennoch.

Wo also liegt der Kern des Widerspruchs zwischen 1. und 2.?

Wohl darin, dass wir immer (noch) versucht sind, mit dem Unendlichen zu rechnen:

unendlich (die Anzahl aller Brüche) minus unendlich (die Anzahl aller natürlichen Zahlen) = weniger

Vgl.                    17                                               minus       4                                                                   =      13

(Vgl. auch oben "unendlich mal unendlich = ???".

Wohlgemerkt: genau das, nämlich rechnen, tut Cantor nicht, sondern er zählt nur.)

Kommen wir damit zu unserer Feststellung oben zurück, dass in dem Regalschema viele Brüche mehrfach, ja sogar unendlich oft vorkommen. Angenommen mal, wir nehmen alle diese mehrfach aufgeführten Brüche aus dem Regal heraus. Dann gibt es drei Möglichkeiten:

1. : es bleiben nur endlich viele Brüche über, die dann aber auch abzählbar sind, nur dass das Abzählen irgendwann aufhört. Diese erste Möglichkeit ist aber ausgeschlossen, da wir ja schon allein wissen, dass es unendlich viele natürliche Zahlen gibt, die eine Teilmenge der Brüche sind, so dass es auf jeden Fall auch unendlich viele verschiedene Brüche gibt.
2. : wir streichen endlich viele Brüche, d.h. wir schneiden aus unserer Perlenkette einige wenige Brüche heraus. Dann bleibt der "Rest" aber eine unendlich lange Perlenkette, die wiederum abzählbar ist, auch wenn wir mit dem Zählen nie fertig werden. Auch diese zweite Möglichkeit ist allerdings ausgeschlossen, da wir ja z.B. schon allein unendlich viele Erweiterungen von ¹/₂ herausschneiden.
3. und die einzig zutreffende, aber allemal auch die interessanteste Möglichkeit: wir schneiden aus der Perlenkette unendlich viele Perlen heraus und es bleiben dennoch unendlich viele übrig. Dann ergibt sich "nur" eine neue, aber wieder unendlich lange, eindimensionale, also abzählbare Perlenkette.

(Ein Beispiel: wir schneiden jede zweite Perle heraus, also beispielsweise jede, die beim Abzählen eine ungerade Nummer erhält. Dann bleiben alle Perlen mit gerader Nummer übrig, d.h. es ergibt sich wieder eine unendlich lange, eindimensionale, also abzählbare Perlenkette. Wir müssen nur neu zählen, d.h. die ehemals erste Perle bleibt zwar die erste, aber die ehemals dritte wird die zweite, die ehemals fünfte die dritte ...).

Anders gesagt:

unendlich (z.B. die Anzahl aller Brüche) minus unendlich (z.B. die Anzahl aller natürlichen Zahlen) = gleichviel.

Bzw.

• s. 1.: unendlich minus unendlich =     endlich  (weniger)
• s. 2.: unendlich minus     endlich =  unendlich (gleichviel)
• s. 3.: unendlich minus unendlich =  unendlich (gleichviel)

Wie gesagt, ist die letzte Zeile die für uns interessanteste, wenn auch irritierendste. Im Folgenden werden wir aber sehen, dass sie dennoch erstaunlicherweise auch fallweise falsch sein kann. Die interessanteste Erkenntnis Cantors folgt nämlich erst noch.

Wenn man sich erstmal an das gehirnausrenkende Faktum gewöhnt hat, dass es gleichviele Brüche wie natürliche Zahlen gibt, wird man ja wohl streng nach dem Motto "kennste ein unendlich, kennste alle unendlich" meinen, dass auch der nächstgrößere Zahlbereich, nämlich die reellen Zahlen, abzählbar ist (sind)

(das würde einen schon gar nicht mehr erstaunen, obwohl doch die Brüche eine echte Teilmenge der reellen Zahlen sind).

Nun hat aber Cantor gezeigt

(zum Beweis siehe ; und da frage ich mich inzwischen, ob man in einem nächsten Schritt auch diesen Beweis noch anschaulicher machen könnte;

nebenbei: auch in diesem Beweis rechnet Cantor nicht mit dem Unendlichen),

Wiederum schön und langweilig, aber was heißt das?

Es bedeutet schlichtweg:

bzw.

Cantor hat also - man höre und staune! - verschiedene Stufen der Unendlichkeit entdeckt:

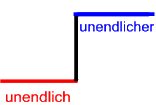
Das aber ist

(wo wir mit "unendlicher" schon in einen superlativistischen Ton verfallen sind)

wohl noch erheblich

"gehirnausrenkender"

als Cantors Entdeckung, dass es gleich (abzählbar) viele Brüche wie natürliche Zahlen gibt, und vor allem mit diesen Stufen der Unendlichkeit haben wohl viele seiner Mathematiker-Zeitgenossen größte Schwierigkeiten gehabt.

(Nebenbei: solche "Schlangenmenschen" wie in der Fotomontage oben nennt man auch "Kontorsionisten" [lat. contortio = Verdrehung, was lustigerweise fast wie "Cantor" klingt: mathematische Schlangenmenschen sind also solche, die fähig sind, einen Knoten im Kopf zu machen - und Cantor gedanklich zu folgen.)

Allerdings hat einer seiner allergrößten Mathematiker-Zeitgenossen, nämlich David Hilbert, immer sowohl menschlich als auch mathematisch zu Cantor gehalten:

„Aus dem Paradies [der Unendlichkeiten], das Cantor uns geschaffen, soll uns niemand vertreiben können.“

Mit den ersten beiden Stufen stellen sich aber die Doppelfrage,

1. , ob es für weitere (welche, wieviele?) Zahlbereiche noch mehr (oder sogar unendlich viele?) Stufen der Unendlichkeit gibt:

,

2. , ob es zwischen der ersten und der zweiten Stufe noch eine (oder mehrere oder gar unendlich viele ?) Zwischenstufe(n) gibt:

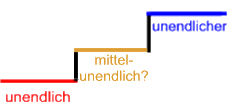
Dass es solch eine Zwischenstufe nicht gibt, ist Cantors ebenfalls berühmte und bis heute unbewiesene "Kontinuumshypothese". Und diese "Kontinuumshypothese" ist immerhin das erste und somit wohl wichtigste der berühmten "Hilbertschen Probleme".

Ein kleiner "Nachbau" des Cantorschen Diagonalverfahrens:

(... was ein wenig an erinnert: da "geht" man auch entlang der aneinandergereihten kleinen Teil-Würfel durch den großen Gesamt-Würfel).

Als dann das anfängliche Quadrat in eine lange Reihe eingeordnet war, habe ich doch gestaunt, wie klein das Quadrat (20 cm • 20 cm) und wie lang die Reihe war (2 m). Und prompt sagte mein sechsjähriger Sohn von sich aus, er glaube nicht, dass die lange Reihe wieder in das Quadrat "zurück" passe.

So anschaulich habe ich noch gesehen, wie explosiv das "Quadrieren" ist!