die Erfindung der Dezimalzahlen

Vorbemerkung
Hauptteil

Vorbemerkung

Das Buch hat mich zu vier Essays angeregt:

    1. dem hier vorliegenden Essay ,
    1. ,
    1. xxx
    1. xxx

Womit sich doch die Frage stellt:  

Hauptteil

Beim Begriff „Dezimalzahl“ herrscht eine für die Mathematik ungewöhnliche

(und sehr sympathische!)

:

In selben Sinn werden Dezimalzahlen auch auf zwei renommierten Internetseiten verstanden:

In diesem ersten Sinn sind also

(z.B. 123,4),

(z.B. 123xx)

Dezimalzahlen.

Ein Grund für dieses Verständnis von "Dezimalzahlen" könnte die Nähe des Begriffs "Dezimalzahl" zum Begriff "Dezimalbruch" sein:

Das da genannte Beispiel suggeriert, dass

 Vergessen wird dabei allerdings oft, dass auch natürliche, also Nicht-Komma-Zahlen als (Dezimal-)Brüche schreibbar sind, also z.B.

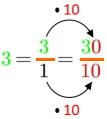
oder kurz

,

so dass z.B. 3 auch ein Dezimalbruch bzw. als solcher schreibbar ist - und also auch eine Dezimalzahl?

Man könnte auch sagen: die natürliche Zahl 3 ist wegen zwar auch als Bruch schreibbar, aber letztlich doch nur ein "Schein-Bruch" , denn bei "richtigen" Brüchen müssen doch gefälligst kleine Bruchstücke (Teile von einem Ganzen) übrig bleiben:

(Nebenbei: auch bei den Dezimalbrüchen herrscht eine babylonische Sprachverwirrung:

“Ein Dezimalbruch oder Zehnerbruch ist ein Bruch, dessen Nenner eine Potenz von Zehn mit natürlichzahligem Exponenten ist – oder, einfacher ausgedrückt, ein Bruch, in dessen Nenner 10 (101), 100 (102), 1000 (103) usw. steht.“;

"Allgemeiner [!] können auch nicht abbrechende (unendliche oder auch periodische) Dezimalzahlen (wie bspw. 0,11111...), die sich offensichtlich nicht [!] als Bruch mit einer Zehnerpotenz im Nenner schreiben lassen, oder auch [sogar] irrationale Zahlen (wie die Kreiszahl π oder die eulersche Zahl e) als Dezimalbruch bezeichnet werden.",

so dass letztlich alle in Dezimalschreibweise geschriebenen Zahlen als Dezimalbrüche bezeichnet werden können.)

,

worauf die harsche Antwort folgt:

In diesem zweiten Sinn sind also

(z.B. 123,4),

(z.B. 123xx)

Dezimalzahlen.

(Nebenbei: es gibt seltene Fälle, in denen natürliche, also Nicht-Komma-Zahlen scheinbar unnötigerweise dennoch mit Komma und einer nachfolgenden Null geschrieben werden, nämlich z.B. . Diese Schreibweise soll wohl besagen:

„Die Durchfahrt ist genau 3 Meter hoch - und keinen Millimeter mehr. Versuchen Sie also erst gar nicht, hier mit einem LKW durchzufahren, der »nur ein bisschen« höher als 3 m ist [»es wird schon gutgehen«], oder versuchen Sie es ruhig, und Sie werden schon sehen, was Sie davon haben: .“

Bei Preisen gibt es zudem die Darstellung einer "glatten", also natürlichen Zahl als .)

Weil auch meine Hauptquelle (s.u.) unter Dezimalzahlen echte Kommazahlen versteht, werde ich den Begriff "Dezimalzahl" im Folgenden dennoch im ersten, engen Sinn verwenden, also für Kommazahlen mit echten Nachkommastellen

(statt nur einer Null wie in ).

Ich finde es immer mal wieder schade, wenn ich erst nach vielen Jahren der Beschäftigung mit Mathematik zu ganz simplen, aber doch wichtigen Erkenntnissen komme

(sei‘s, dass ich selbstständig zu diesen Erkenntnissen komme

[z.B. Kathetensatz und ],

sei‘s, dass ich in Büchern über sie stolpere

[z.B. unten in ]):

wie konnte ich so lange so (betriebs-)blind für (allzu) Offensichtliches sein?

Zwei Beispiele:

  1. : ich habe u.a. in Vor- und auch einige Nachteile der Bruchrechnung (und Bruchschreibweise) aufgezeigt und darauf hingewiesen, dass je nach innermathematischer oder außermathematischer (Anwendungen) Situation mal Brüche, mal Dezimalzahlen Vorteile haben. Allerdings habe ich dabei bis jetzt den vielleicht größten Nachteil der Brüche gegenüber den Dezimalzahlen übersehen:

Dezimalzahlen lassen sich viel einfacher vergleichen.

Ein Beispiel:

Welcher der beiden Brüche und ist größer?

Oder sind sie vielleicht sogar gleich groß? Denn schließlich

Um die beiden Brüche vergleichen zu können, ist es ratsam, beide erstmal weitestmöglich zu kürzen:

=

Insgesamt erhalten wir also

          =                 und          =               ,

woraus folgt:

          =                  <             =              

oder kurz

                                       <                                      .

Erst nach so umständlichen Rechnungen wissen wir also, dass der anfängliche erste Bruch kleiner als der anfängliche zweite Bruch ist.

(Nebenbei: weil der Nenner 119 des ersten Bruchs nur geringfügig kleiner als der Nenner 121 des zweiten Bruchs ist, wissen wir aber auch schon, dass die beiden anfänglichen Brüche und fast gleich groß sind

[wobei "minimal" und "fast" allerdings subjektive Begriffe sind].)

Kurz und bündig:

  der Größenvergleich zweier Brüche kann enorm aufwendig sein.

Wenn wir nun die Brüche und vom Taschenrechner ausrechnen lassen, erhalten wir die Dezimalzahlen

(Hierbei soll es uns egal sein, dass der Taschenrechner bei beiden Dezimalzahlen am Ende weitere Nachkommastellen abschneidet und deshalb eigentlich das Ungefährzeichen ≈ stehen müsste

Für den Größenvergleich der beiden Dezimalzahlen 1,545454545... und 1,571428571... ist es einzig und allein entscheidend, ob und wenn ja an welcher Nachkommastelle sie sich erstmals unterscheiden:

die zweite Nachkommastelle der ersten Zahl (also 4) ist kleiner als die zweite Nachkommastelle der zweiten Zahl (also 7).

Es reicht also eigentlich 1,54... < 1,57...  

Und damit ist insgesamt die erste Zahl 1,545454545... kleiner als die zweite Zahl 1,571428571...

(wobei der Unterschied - wie oben vorausgesehen - geringfügig, nämlich nur ca. drei Hundertstel ist).

Kurz und bündig:

  der Größenvergleich zweier Dezimalzahlen ist sehr einfach

(es sei denn, die beiden hinter dem Komma ellenlangen Dezimalzahlen unterscheiden sich gar nicht oder erst an einer sehr späten [z.B. der hundertsten] Nachkommastelle).
  1. und der eigentliche Anlass dieses Essays:

Zitat aus dem oben schon genannten Buch :

„Hatte der Mensch je etwas Schnelleres erschaffen? Schnurgerade wie ein Pfeil sauste es über den Strand in Scheveningen an der Küste bei Den Haag und erreichte bis zu 40 Stundenkilometer. Ein Fahrgestell mit vier großen Wagenrädern trug den Rumpf, der 20 oder mehr tollkühnen Passagieren Platz bot. Der Wind in den breiten Rahsegeln an den beiden Masten trieb das Gefährt über den Sand voran, und als Statthalter Prinz Moritz, Zweitgeborener des ermordeten Königs Wilhelm des Schweigers, das Steuer übernahm, flatterte die Prinzenflagge des Hauses Oranien am Mast. Bei kräftiger Brise schoss der zeilwagen (Segelwagen) am Strand entlang, scheuchte die Möwen auf und legte ein Tempo wie der Wind vor, sodass die Passagiere keinen Fahrtwind mehr auf ihren Gesichtern spürten, wie ein französischer Augenzeuge 1606 berichtete. Dieses erstaunliche Wunderwerk der Technik hatte Simon Stevin erdacht und erbaut, höchstwahrscheinlich angeregt von Illustrationen wesentlich älterer chinesischer Segelwagen, die der flämische Kartograf Gerard Mercator nach den Beschreibungen damaliger Forschungsreisender in seinen wunderschönen Atlanten abgebildet hatte. In Laurence Sternes Tristram Shandy schwärmt Onkel Toby in einer Passage ebenfalls von dem »berühmten Segelwagen, der dem Prinzen Maurice gehörte und der von so wundervoller Konstruktion und Geschwindigkeit war, dass er ein halbes Dutzend Personen in ich weiß nicht wie wenigen Minuten dreißig deutsche Meilen beförderte«, obgleich er den Wagen schwerlich selbst gesehen haben kann, wenn er denn tatsächlich, wie er ja beharrlich behauptet, in der Schlacht von Namur (1695) gekämpft hat.


Stevin war der Prototyp des niederländischen Wissenschaftlers schlechthin, ein vorzüglicher Mathematiker, dem es vor allem um den praktischen Nutzen seiner Arbeit ging. 1581 war er als 33-Jähriger aus seiner Heimatstadt Brügge nach Leiden geflüchtet und veröffentlichte dort in rascher Folge Bücher über Arithmetik, Geometrie, Maßsysteme, Buchhaltung, Mechanik und Hydrostatik (die Lehre von unbewegten, strömungsfreien Flüssigkeiten). Daneben verfasste er angewandte und praxisbezogene Schriften, in denen er sich beispielsweise mit Idealentwürfen für Festungen und Schleusen beschäftigte. Er unterrichtete nicht an der Universität und verdiente sein Geld durch die Verbesserung von Windmühlen oder Wasserbauprojekten, ohne dass diese Tätigkeit seine wissenschaftlichen Interessen behindert hätte. In gewissem Sinn war seine Situation sogar kennzeichnend für den Zustand der Niederlande, denn »dass keine wissenschaftlichen oder philosophischen Glaubenskriege geführt wurden, (…) bot vielfältige Gelegenheiten für neue Ideen«. Das dichte kommerzielle und kulturelle Netzwerk in den selbstbewussten Städten trug in erster Linie und in viel größerem Umfang als die akademischen Institutionen zur Entstehung und Verbreitung neuer Ideen bei.
Und es waren wirklich neue Ideen. Stevin schuf sozusagen den Segelwagen der Buchhaltung mit seinem Vorschlag, statt der bis dahin üblichen gewöhnlichen Bruchzahlen mit einer Vielzahl möglicher Nenner Dezimalzahlen einzuführen. Zuvor hatte ein Händler, der seine täglichen Einnahmen aufrechnete, mit Preisangaben zu kämpfen, die, je nach den unterschiedlichen Währungen, in Dritteln, Achteln, Fünfzehnteln oder Sechzigsteln angegeben waren. In seinem Lehrbuch De Thiende (»Das Zehntel«) aus dem Jahr 1585 setzte Stevin eine eingekreiste Null neben eine Zahl, um die verschiedenen Potenzen der Zehntel darzustellen (um tatsächlich also zu zeigen, dass die Gesamtzahl durch zehn hoch null geteilt wurde — oder mit anderen Worten unverändert blieb). Eine umkreiste Eins stand für Zehntel (geteilt durch zehn hoch eins), eine umkreiste Zwei repräsentierte Hundertstel (geteilt durch zehn hoch zwei) und so weiter. 30 Jahre später entwickelte der schottische Mathematiker John Napier Stevins Schreibweise weiter zur uns heute vertrauten Form der Kommasetzung oder des Punktes, durch den die Bruchteile der jeweiligen Zahl von der Zahl selbst abgetrennt werden. Die eingekreisten Zahlen waren damit überflüssig, aber das Prinzip der aufeinanderfolgenden Zehnerpotenzen war zu diesem Zeitpunkt bereits etabliert. Die irrationale Kreiszahl, in Napiers System dargestellt als 3.1416 (…), sieht in Stevins Notation so aus: 3(0)1(1)4(2)1(3)6(4). Im Jahr 1590 trat Stevin als Quartiermeister der Armee in den Dienst des Statthalters Prinz Moritz. Er beschäftigte sich mit militärischen Vermessungen und passte die Konstruktion italienischer Festungsbauten aus der Renaissancezeit an die geografischen Bedingungen der Niederlande an. Die ursprünglichen Trockengräben ersetzte er dabei durch Kanäle oder Wassergräben und errichtete die fortschrittlichsten Festungsanlagen Europas an der sich ständig verschiebenden Südgrenze zwischen der Republik der Niederlande und den Spanischen Niederlanden. Im Jahre 1600 gründete Stevin auf Wunsch des Statthalters eine Schule für Ingenieure in Leiden. Dort wurde, auf seine Entscheidung hin, Unterricht auf Niederländisch statt Latein erteilt. Die Ingenieurskunst war bald als »dytsche mathematycke« oder niederländische Mathematik bekannt. Der berühmteste Lehrer der Schule war Frans van Schooten, dessen gleichnamiger Sohn später Christiaan Huygens in Mathematik unterrichtete. Stevin ging es in erster Linie um den praktischen Nutzen seiner Arbeiten, und auch rein mathematische Disziplinen wie die Geometrie sollten dem Wohl der ganzen Nation dienen. Durch die Veröffentlichung seiner Lehrbücher hoffte er, dass viele seinem Beispiel folgen würden. Eines dieser Bücher, verfasst für Prinz Moritz, Van de Deursichtighe (»Über die Perspektive«), ist bemerkenswert wegen der ausschließlich rationalen Analyse künstlerischer Geheimnisse und enthält unter anderem den Entwurf für ein Gerät zum räumlichen Sehen; auf einer Glasplatte konnte man akkurat die sich dahinter befindende Szene wiedergeben. Prinz Moritz zeigte sich so beeindruckt von dieser Idee, dass er sich ein solches Modell anfertigen ließ. Stevins wichtigstes Vermächtnis sind jedoch weder der Segelwagen noch die Dezimalzahlen, sondern die Einführung einer Wissenschaftssprache in den Niederlanden. Er veröffentlichte seine Schriften in der Landessprache, damit Bauherren, Handwerker und Händler sie lesen konnten. Beispielsweise widmete er De Thiende den »Sternenbeobachtern, Landmessern, Tuchmessern, Weinmessern, Messleuten im Allgemeinen, Münzmeistern und allen Kaufleuten«. Dass er nur wenige Jahre nachdem sich die Nordprovinzen von der spanischen Krone getrennt hatten, in Niederländisch schrieb, war auch ein stolzes Bekenntnis zur nach wie vor bedrohten Unabhängigkeit seines Heimatlandes.
Und dabei ließ es Stevin nicht bewenden. In Beghinselen der Weeghconst (»Prinzipien des Wiegens«, 1586) formulierte er seine Überzeugung, das Niederländische sei die ideale Wissenschaftssprache, weiter aus. Er kam zu diesem Schluss, weil das Niederländische über eine ungewöhnlich große Anzahl an einsilbigen Wörtern verfügt, die sich nötigenfalls zu längeren Wörtern zusammensetzen lassen. Stevin vertrat sogar die ziemlich steile These, die Menschen hätten sich in einer imaginären wijsentijt, dem Zeitalter der Weisheit lange vor dem antiken Griechenland, als der Mensch noch allwissend war, miteinander auf Niederländisch verständigt. Stevins Begriffe, mit denen er die einzelnen Bereiche der Naturwissenschaften bezeichnete, spiegeln seine Argumente wider. Physik bezeichnet er als natuurkunde, also das Wissen über die Natur. So gut wie keine andere Sprache außer dem Niederländischen hat einen eigenständigen, nicht vom griechischen physika abgeleiteten Begriff für Physik. Andere Wortschöpfungen sind noch ehrgeiziger und erheben nicht nur Anspruch auf die Urheberschaft über einen Zweig der Wissenschaft, indem sie den griechischen oder lateinischen Namen verwerfen, sondern auch, indem sie auf einen subtilen Zusammenhang zwischen dem Nachweisbaren und dem Wissenschaftlichen verweisen. So wird die Mathematik zur wiskunde, was man als Lehre des gesicherten Wissens übersetzen kann. Chemie ist die scheikunde, also die Lehre vom (Unter-)Scheiden, ein Hinweis auf den sich abzeichnenden Richtungswechsel hin zu einer analytischen Wissenschaft und eine höchst sinnvolle Alternative zum Begriff Chemie, denn die etymologische Nähe zur unseriösen Alchemie wird aufgehoben.
Zum Vergleich: Das Oxford English Dictionary nennt 1605 als das Jahr, in dem chemistry zum ersten Mal im Englischen auftaucht, zeitgleich mit Stevins wissenschaftlichen Fachbegriffen; im Englischen bezeichnet der Begriff sowohl die Alchemie als auch die gerade entstehende Wissenschaft der Chemie. Bis heute muss sich das englische chemistry mit wenig hilfreichen sekundären Bedeutungsebenen wie »geheimnisvolle Wirkung oder Verwandlung« und »instinktive Anziehung« zwischen zwei Menschen herumschlagen. Die »Astronomie« hat ähnliche Probleme. Ursprünglich, als ein Teilbereich der sogenannten klassischen freien Künste (Quadrivium), bezeichnete der Begriff die Wissenschaft von der Bewegung der Sterne und Planeten sowie deren Einfluss auf Natur und Mensch — eingeschlossen jener Pseudowissenschaft, die wir als Astrologie bezeichnen. Das Englische kämpft immer wieder gegen diese frühere Doppelbedeutung an; Stevins Begriff der sterrenkunde, der Sternkunde, umschifft das Problem dagegen elegant.
Stevin erfand oder warb auch für unzweideutige, beschreibende Begriffe innerhalb der von ihm benannten Disziplinen, beispielsweise driehoek (Dreieck) statt Triangel und lanckrondt (Langrund) statt Ellipse. Ein Trapez wird zum bijl, das niederländische Wort für Axt, und damit wesentlich anschaulicher. Wahrscheinlich ist kein Begriff so kennzeichnend für Stevins vor allem praktisches Verständnis von Wissenschaft wie seine etwas verschmitzte Wortwahl für »Theorie«, nämlich spiegeling. Wörtlich übersetzt also »Spiegelung«, etwas freier und taktvoller auch »Reflexion«; und noch freier, aber provokanter einfach nur »in der Kristallkugel lesen«.“

Für meinen Geschmack fehlen da nur noch einige Bilder:


 * 1548/49  + 1620

und darin


(denn schließlich ist das anscheinend die erste jemals gedruckte Dezimalzahl)

Nun kann man sich natürlich fragen, was die doch ziemlich lange Passage über Simon Stevin in einem Buch zu suchen hat, das doch eigentlich von Christiaan Huygens handelt.

Die Antwort folgt direkt auf das obige Zitat:

„Wollte man Stevin als den Prototypen bezeichnen, wäre Christiaan Huygens das ausgereifte Produkt. Stevin hatte den Beweis geliefert, dass sich auch außerhalb der Universität ein intellektuell äußerst ergiebiges Leben führen ließ, vorausgesetzt, es fand sich ein entsprechender Mentor. Wie Stevin war Huygens vor allem am praktischen Nutzen seiner Arbeit gelegen. Seine Arbeit beruhte, wie die von Stevin, auf grundlegenden mathematischen Methoden in den Grenzbereichen zwischen Mechanik, Geometrie und Optik. Ein vielseitiger niederländischer Mathematiker bestellte gleichsam das Feld für seinen Nachfolger in genau den Wissenschaftszweigen, in denen der andere es später zu höchsten Ehren bringen sollte. Ein halbes Jahrhundert nach Stevin wird man Huygens als den größten Mathematiker, Astronomen und Physiker seiner Zeit feiern.“

Wie schon der Titel

die Erfindung der  Dezimalzahlen

dieses Essays klarmacht, interessiert mich an dem langen Zitat aus dem Buch hier nur der Ausschnitt

  „Stevin schuf sozusagen den Segelwagen der Buchhaltung mit seinem Vorschlag, statt der bis dahin üblichen gewöhnlichen Bruchzahlen mit einer Vielzahl möglicher Nenner Dezimalzahlen einzuführen. Zuvor hatte ein Händler, der seine täglichen Einnahmen aufrechnete, mit Preisangaben zu kämpfen, die, je nach den unterschiedlichen Währungen, in Dritteln, Achteln, Fünfzehnteln oder Sechzigsteln angegeben waren [und deshalb nur nach umständlichem Gleichnamig-Machen (s.o.) vergleichbar waren]. In seinem Lehrbuch De Thiende (»Das Zehntel«) aus dem Jahr 1585 setzte Stevin eine eingekreiste Null neben eine Zahl, um die verschiedenen Potenzen der Zehntel darzustellen (um tatsächlich also zu zeigen, dass die Gesamtzahl durch zehn hoch null geteilt wurde — oder mit anderen Worten unverändert blieb). Eine umkreiste Eins stand für Zehntel (geteilt durch zehn hoch eins), eine umkreiste Zwei repräsentierte Hundertstel (geteilt durch zehn hoch zwei) und so weiter. 30 Jahre später entwickelte der schottische Mathematiker John Napier Stevins Schreibweise weiter zur uns heute vertrauten Form der Kommasetzung oder des Punktes, durch den die Bruchteile der jeweiligen Zahl von der Zahl selbst abgetrennt werden. Die eingekreisten Zahlen waren damit überflüssig, aber das Prinzip der aufeinanderfolgenden Zehnerpotenzen war zu diesem Zeitpunkt bereits etabliert. Die irrationale Kreiszahl, in Napiers System dargestellt als 3.1416 (…), sieht in Stevins Notation so aus: 3(0)1(1)4(2)1(3)6(4).“

Verdammt! Warum wusste ich das bislang nicht?

(U.a.: was ist das für ein Mathematikstudium, in dem der Name „Stevin“ nie vorkam?)

Aber was ist da überhaupt wissenswert?: sicherlich nicht nur ein weiterer inhaltsleerer Name, also „Stevin“

(vgl. ),

sondern Hintergründe, über die allerdings leider kaum mehr bekannt zu sein scheint als das im obigen Zitat aus dem Buch Gesagte:

Am einfachsten zu beantworten ist die letzte Frage, also

"welche Bedeutung hat in der Mathematik bis heute?",

weil diese Frage die einzige ist, die nur wir mit unserem historischen Abstand beantworten können:

Stevins Dezimalzahlen à la haben

(allerdings in Napiers Kommaschreibweise 237,578)

bis heute einen Siegeszug ohnegleichen hingelegt, und zwar vor allem außerhalb der Fachwissenschaft Mathematik

(in der aus guten Gründen noch sehr viel mehr mit den ansonsten verdrängten Brüchen gerechnet wird),

ja, dieser Siegeszug hat sich im Zeitalter der Computer sogar noch beschleunigt:

(denn Computer können überhaupt nicht mit Brüchen rechnen):

Stevins Dezimalzahlen

(s.o.: "[...] widmete er De Thiende den »Sternenbeobachtern, Landmessern, Tuchmessern, Weinmessern, Messleuten im Allgemeinen , Münzmeistern und allen Kaufleuten [...]«)

Auf die anderen oben gestellten Fragen kann ich aber nur hypothetische Antworten geben

(vgl. ),

was auch daran liegt, dass

Mich interessieren im Folgenden aber nur die "mathematischen" Fragen

  1. was [...] waren bei [...] die in seiner Zeit bekannten mathematischen Voraussetzungen, auf denen er aufbauen konnte [...]?
  2. worin bestand bei seine eigene, neue Leistung?
  3. wie ist er "drauf" gekommen?

Vorweg aber zur Frage, ob Stevin denn tatsächlich als erster die Dezimalzahlen erfunden hat:

mir ist kein Gegenbeleg bekannt

(also jemand, der diese Dezimalzahlen schon vorher eingeführt hat; und selbst wenn es so war, muss Stevin das ja nicht gewusst, kann er die Dezimalzahlen also nochmals erfunden haben, wodurch seine Leistung nicht im mindesten geschmälert würde, und zwar selbst dann, wenn er "nur" den kleinen, aber entscheidenden "Kick" geliefert hat).

Dennoch gibt es genug Beispiele dafür, dass (u.a. mathematische) Erfindungen / Entdeckungen gar nicht neu waren und manchmal die Falschen (späteren Erfinder / Entdecker) berühmt geworden sind. Nur drei Beispiele:

“Es ist nach dem […] französischen Mathematikers René Descartes benannt, der das Konzept der »kartesischen Koordinaten« bekannt [!] gemacht hat.“
(Quelle: );

Interessant ist aber auch:


(Oresme-Diagramme aus der Textsammlung
"Questio de modalibus"
von Bassano Politi, 1505)

Damit aber zu den oben gestellten drei Fragen:

Zu 1., also der Frage nach den Voraussetzungen, auf denen Stevin aufbauen konnte - und auch tatsächlich aufgebaut hat.

Zumindest eines dieser Fundamente ist eindeutig identifizierbar: die Schreibweise aus der ersten Ausgabe von Stevins Buch „De Tiende“ beweist:


Leonardo da Pisa alias Fibonacci
(* um 1170  † nach 1240)

zu uns gekommene Dezimalsystem inkl. der darin wichtigsten Zahl, nämlich merkwürdigerweise der Null   ,

Der Anfang von , nämlich , zeigt den Stand bis direkt vor Stevin: ist die Zahl, die wir bis heute als

„hundertundßig“

bezeichnen. Oder mit der richtigen Reihenfolge der Ziffern

„hundretty“.

€ in -Münzen sind .

Das ist aber so unübersichtlich, dass es genauso gut 196 € oder € sein könnten.

Wenn wir also wissen wollen, wie viele Euro es exakt sind,

(auf die Gefahr hin, dass wir uns [z.B., wenn wir gestört werden] verzählen und dann nochmals von vorne beginnen müssen)

Ein solche Lege-System ist eben das Zehnersystem, d.h. wir legen erstmal 10 -Münzen untereinander

(genauso könnten wir z.B.

Zehn -Münzen untereinander sehen so aussehen:

Wenn wir alle Münzen derart (in 10 Zeilen untereinander) anordnen, erhalten wir

Dieses Verfahren hat

(nur bei der letzten Spalte und damit der letzten Ziffer können wir uns sicher sein).

Das Problem ist also, dass wir

Nun könnten wir natürlich auch noch die Spalten (1 ... 23 volländige + )  durchzählen

(wieder mit der Gefahr, uns zu verzählen),

oder wir wählen in Analogie zum Schachfeld (8 Zeilen und auch 8 Spalten) jetzt 10 Zeilen und auch 10 Spalten, legen also (solange möglich) 10x10-Quadrate:

                             

Weil das aber doch arg viele Münzen sind, helfen wir uns mit Papiergeld:

                               

Das aber ist nun endlich übersichtlich.

Noch kürzer sind

• +  • + •

und

• 100   +  • 10 + •   1  .  

Weil wir die Münzen teilweise quadratisch angeordnet hatten, können wir auch

• 102 +  • 10    + •    1    

und dann systematisch schreiben:

• 102 +  • 101 + •   100 

(wobei hier nicht erklärt werden soll, weshalb 100 = 1 ist).

In Stevins Schreibweise mit für • 100

(was ja schon eine erheblich Abstraktion ist):

• 102 +  • 101 +         .

Ausschließlich in -Münzen hatten wir oben

                             

erhalten, also

• = • 1 € = • 100 € = €

Wie wir noch sehen werden, gibt es aber auch Indizien dafür, dass Stevin mit einer umkreisten Zahl "nur" gemeint hat, an welcher Nachkommastelle die direkt davor stehende Ziffer steht

(wobei er das Komma als allerdings noch gar nicht als mathematisches Zeichen kannte).

Im Fall würde dass heißen, dass an der ten Nachkommastelle steht, also nur Vorkommastellen hat - und somit eine natürliche / ganze Zahl ist.

Und so lässt sich

Das Dezimalsystem für natürliche bzw. ganze Zahlen war aber schon vor Stevin gut erarbeitet worden, und darauf konnte er nun aufbauen.

Anders gesagt: an

Zu 2., also der Frage: worin bestand bei Stevins eigene, neue Leistung?

Anders gefragt: was bedeutet das Ende von , also ?

Oben wurde schon angedeutet:

Damit erhalten wir mit Napiers bis heute üblicher Kommaschreibweise:

Schön und gut, aber damit wissen wir noch immer nicht, was es bedeutet, dass eine Ziffer auf der ersten / zweiten / dritten Nachkommstelle steht.

(Wir wissen es heute sehr wohl, da wir uns

Z.B. weiß heute jeder, was m sind:

m + dm + cm + mm

[Merkwürdigerweise kommt aber die Einheit „dm“ (Dezimeter) in unserem aktiven Wortschatz gar nicht vor, denn statt „ dm“ würden wir immer „0 cm“ sagen, bei unserem Beispiel also

m +           cm + mm]

Wie schwierig es für Anfänger und vermutlich auch ihre Entdecker es ist, mit dem Dezimalsystem und Dezimalzahlen umzugehen, wird deutlich,

Und was bedeutet dann im Dualsystem erstmal eine Kommazahl wie z.B. 1101,0101?)

Welch enorme Leistung Stevin vollbracht hat, wird aber erst deutlich, wenn wir uns der dritten Frage zuwenden:

Zu 3., also der Frage „wie ist Stevin »drauf« gekommen?“

Da mir weitere Hintergrundinformationen zu Stevin fehlen, ist dies der hypotetischste Teil.

 Dazu zwei Exkurse vorweg:

 
  1. Gab es vor 400 Jahren

(also zu Stevins [und Huygens‘] Zeit)

überhaupt schon ausschließlich „reine“ Mathematiker, also solche, denen jegliche außermathematische Anwendung herzhaft egal war?

(Immerhin ist z.B. von Fermat

[einem Zeitgenossen Stevins)

bekannt, dass er sich zumindest phasenweise mit rein innermathematischen Problemen beschäftigt hat.)

Der obigen Biographie Stevins lässt sich entnehmen, dass Stevin sehr praktisch gedacht hat

(sogar bei seinen Vorschlägen für eine einheitliche Wissenschaftssprache).

Worauf meine Frage nach den praktischen Zugängen zur Mathematik damals hinausläuft:

war die praktische Anwendbarkeit von Stevins Dezimalzahlen nicht nur eine Folge (ein „Abfallprodukt“), sondern auch die Ursache seiner mathematischen Überlegungen?

Überhaupt scheint mir, dass Stevins Vorgehensweise mit Schülern besser hypothetisch rekonstruiert werden kann, wenn sie praktisch und damit anschaulich erarbeitet wird.
     
   



(Kolumbus entdeckt [?] Amerika)

„
Die ganzen Zahlen hat der liebe Gott gemacht,
alles andere [Brüche und Dezimalz ahlen ...] ist Menschenwerk.“
(Leopold Kronecker)

Es lässt sich ja schon darüber streiten, ob "der liebe Gott" immerhin die ganzen Zahlen erschaffen hat, womit wohl gemeint ist:

die ganzen Zahlen waren schon da, bevor "der" Mensch sie entdeckt hat

(und wenn die anderen Zahlen nicht vorher da waren, hat der Mensch sie erfunden).

Wenn im Wald ein Baum umfällt
und niemand da ist, der es hört,
macht er dann ein Geräusch?

Angenommen mal, in einem Wald stehen nah beieinander drei Bäume:



Wer aber stellt da die Dreizahl fest? Gibt es also die Zahl 3, ohne dass jemand sie denkt?

(… und sei es ein vorbeikommendes Reh, denn in der Tat können einige Tiere überschaubar viele Gegenstände abzählen [vgl. ].
Peter Wohlleben hat in seinem Buch Forschungsergebnisse referiert, die besagen, dass sogar Bäume miteinander „kommunizieren“ können. Ob sie aber auch wissen, dass sie in einer Dreiergruppe stehen, wissen wir nicht.)
Pythagoras war der Meinung, dass es nur rationale Zahlen gebe, also Brüche aus ganzen Zahlen.

(Es ist hier vorerst nebensächlich, dass sie in Dezimalschreibweise endlich oder periodisch hinter dem Komma sind - und dass es auch irrationale Zahlen gibt. Vgl. .)

Aber gibt es Brüche wirklich

(also außerhalb menschlicher Köpfe),

sind sie von „Gott“ geschaffen, so dass der Mensch sie nur noch entdecken, aber nicht mehr erfinden kann?

Das Innenleben von Muscheln ist für Möwen eine Delikatesse, nur leider sind Muscheln

(solange sie leben)

nur ganz selten schnabelgerecht geöffnet:
, die vor 10 000 Jahren lebte, hat sich eine geschlossene Muschel mal scharf angeschaut und dabei festgestellt, dass es zwischen den beiden Schalen einen feinen Schlitz gab , und wenn Jonathan mit seinem Schnabel oben in diesen Schlitz hackte

("und bist du nicht willig, so brauch' ich Gewalt"),

zersprang die Muschel in zwei fast exakt gleiche Hälften (2 • )    , die Jonathan dann genüsslich ausschlecken konnte.

Nun war Jonathan zwar offensichtlich ein schlaues Kerlchen, aber hat er wirklich wahrgenommen, dass die beiden Schalen gleich große Hälften der ganzen Muschel waren? Ihn interessierte doch vermutlich nur, dass die Muschel nun endlich geöffnet war und er den Inhalt verspeisen konnte.

Konnten die Menschen also nur nachentdecken, was bereits Jonathan (als Erster?) entdeckt hatte?

Und gab es die Hälften auch ohne Jonathan

(so dass auch er sie nur entdecken, aber nicht erfinden konnte)?

Denn schließlich lagen sehr häufig paarweise Muschelschalen am Strand beieinander:

Aber sind das nun zwei Hälften oder drei Drittel?

(... zumal nicht klar ist, ob und wenn ja welche zwei Schalen ursprünglich eine Muschel gebildet haben.)

Mir scheint eher: "Brüche liegen im Auge des Betrachters [der da sortiert]."
(Nebenbei: in Wirklichkeit öffnen Möwen Muscheln anscheinend auf zwei Arten:
  • "Die Muscheln [...]  knacken [...] [die Möwen], indem sie diese verschlucken. «Möwen haben einen ganz starken Magen, der zerdrückt die Muscheln. Das Fleisch wird verdaut, die Schalenreste spucken die Möwen einfach wieder aus» [...]"
  • "Dann kann man unsere Möwen sehen, wie sie die Miesmuscheln von den Buhnen holen und dann entweder auf die Buhne oder auf die Promenade fallen lassen, damit sie kaputt gehen. Dann gibts lecker Muschelessen.")

Garantiert gilt aber

(und darum geht es mir hier vor allem):

die Dezimalzahlen wurden vom Menschen (Stevin?!) erfunden.

(Oder sind Sie schon mal in freier Wildbahn über eine [nicht menschengemachte] Dezimalzahl gestolpert?)

Und damit hat Stevin einen sowohl für Anwendungen als auch die reine Mathematik enorm wichtigen Abstraktionsschritt vollzogen!

(... für die reine Mathematik, weil erst mit Dezimalzahlen nicht-rationale bzw. irrationale Zahlen wie z.B. oder 0, 1 2 3 4 5 6 7 8 9 10 11 ... ansatzweise vorstellbar wurden, nämlich als
  • hinter dem Komma unendliche und unperiodische,
  • also arg chaotische
  • und niemals vollends aufschreibbare
Dezimalzahlen.)

Mal angenommen,

  1. das Dezimalsystem war zu Zeiten Stevins innermathematisch für natürliche bzw. ganze Zahlen bereits fest etabliert und gut verstanden,

  2. gab es bereits Maßeinheiten im Dezimalsystem

(also z.B. km, m, cm, mm).

Dann war der „Schritt über das Komma hinweg“, d.h.

gar nicht so schwierig, sondern naheliegend

(aber sowas sagt sich im Nachhinein allzu leicht):

"That's one small step for [a] man - but - [a] giant leap for mankind."
"Das ist ein kleiner Schritt für einen Mann, aber ein großer Sprung für die Menschheit."

Nehmen wir als Beispiel mal den Zollstock :

so ein Zollstock ist üblicherweise 200 cm lang.

Zwar wird er aus historischen Gründen (s.u.) noch „Zollstock“ genannt, aber in Wirklichkeit ist es bei uns ein Zentimeter-„Stock“, da auf ihm ausschließlich Zentimeterzahlen stehen, also 1 - 2 - 3 - … - 8 - 9 - 10 - 11 - 12 - … - 198 - 199 - 200.

(Die Vielfachen von 10 sind meist größer, aber auch in der Zentimeter- und nicht in der Dezimeter-Zählung [10 cm = 1 dm]: .

Und ebenso wenig taucht auf dem „Zollstock“ eine Meterzählung auf, sondern auch die Meter sind in Zentimeter ausgedrückt: 100 cm = 1 m, 200 cm = 2 m.

Nebenbei:

[wir leben ca. 2000 Jahre nach Christi Geburt]

passende historische Zollstock : da muss man gar niht alle auf dem Zollstock genannten historischen Daten kennen, bekommt aber einen guten Eindruck von den zeitlichen Distanzen besonders wichtiger historischer Ereignisse

[ ≈ 50 cm = 500 mm ≅ 500 Jahre entfernt]

- und von der Kürze des eigenen Lebens.

Inzwischen gibt es auch einen technikhistorischen und einen [für Laien allerdings völlig unbrauchbaren mathematischen Zollstock.)

Angenommen nun, wir messen die Länge einer Holzlatte mit zwei Zollstöcken und brauchen dazu

  • Als erstes lesen wir ab, dss die Holzlatte ungefähr cm lang ist:

    • "ungefähr", weil die Holzlatte offensichtlich "ein wenig" (?) länger als cm ist. Wenn wir deshalb genauer hinschauen   , stellen wir fest, dass die Holzlatte länger als cm ist.

    Daraus schließen wir heute natürlich umgehend, dass die Holzlatte cm lang ist

    (wobei die hinter dem Komma mm bedeutet).

    Das ist uns so selbstverständlich, dass es uns schwer fällt, wieder hinter dieses intuitive Wissen zurück zu gehen. Aber versuchen wir es dennoch mal, indem wir uns klar machen, warum wir heute so problemlos " cm" sagen können:
    1. geht uns das Dezimalsystem so leicht von der Hand, weil wir im Alltag gar kein anderes kennen und es deshalb gerne für das einzig mögliche oder zumindest einzig praktische Zahlensystem halten;
    2. sind unsere Längenmaße ebenso dezimal aufgebaut wie unsere Gewichtmaße und unsere Währung
    (z.B. gilt 1 cm =  10 mm , 1 kg = 1000 g  = 10 • 10 • 10g, 1 € =  100 Cent  = 10 • 10 Cent);
    1. ist uns Stevins Dezimalzahlen-Schreibweise oder genauer Napiers Kommaschreibweise selbstverständlich.
    Zur Zeit Stevins war aber nur 1. halbwegs erfüllt, da sich die arabische Stellenwert-Zahlenschreibweise seit Fibonacci lamgsam durchgesetzt hatte, allerdings nur für natürliche / ganze, also Nichtkommazahlen.

    Zu 3.: den Schritt hin zu Nachkomma-, also Dezimalzahlen hat aber überhaupt erst Stevin vollzogen.

    Für uns interessant ist hier aber vor allem 2.:

    zur Zeit Stevins gab es nirgends in Europa dezimal aufgebaute Längen- und Gewichtsmaße bzw. Währungen. Es gab also auch keinen „Zentimeter-Stock“, an dem Stevin die Dezimalzahlen hätte entdecken können.

    Ja, solch ein „Zentimeter-Stock“ wurde durch Stevins Vorarbeit überhaupt erst möglich - und über zweihundert Jahre nach Stevin mit der Einführung des Meters erstmals Wirklichkeit.

    Es sieht also so aus, dass der ansonsten so praktische Stevin nur auf innermathematischem Weg zu kommen konnte. Dazu musste er aber „nur“ die bereits gängige Vorkommalogik dezimaler natürlicher Zahlen nach dem Komma fortsetzen.

    (Aber von wegen „nur“: das sagt sich [wieder mal] im Nachhinein so leicht. Aber auf dieses Durchbrechen der „Komma-Schallmauer“ und diesen Sprung in eine [damals noch] terra incognita (unbekannte Welt) muss man erst mal kommen!:  

     

         

    Wenn man nun die Exponentenreihe 2 / 1 / 0 ins Negative fortsetzt (also 2 / 1 / 0 / -1 / - 2 / - 3 ), ergibt sich

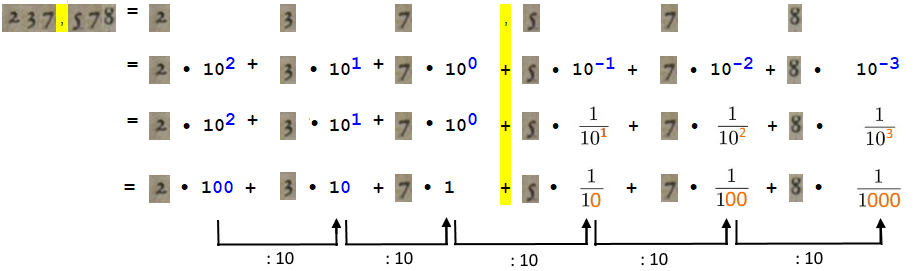
    Daran ist dreierlei bemerkenswert:

      1. ist dieser Gedankengang eben doch nicht ganz so einfach, wie oben kurz suggeriert wurde: um ihn zu verstehen, muss man zumindest das Dezimalsystem für natürliche Zahlen sowie die Potenzgesetze gut verstanden haben (z.B.: warum ist = ? ).
      1. haben wir mit

     

    ein Verfahren, mit dem man von links nach rechts Dezimalzahlen in Brüche umwandeln kann. Die umgekehrte Rechnung, also die Umrechnung beliebiger Brüche in Dezimalzahlen, ist allerdings nicht ganz so einfach.
      1. und im Hinblick auf Stevin am wichtigsten: mit

    sind mir ihm dicht auf den Fersen.

    Da es uns um die Nachkommastellen geht, fassen wir der Einfachheit halber die bereits bestens bekannten Vorkommastellen und  und   zusammen:

     Als Vorbereitung auf das Folgende verändern wir jetzt nur die Zahlenabstände:


    Mit Stevins Zahlen geschrieben:

    Vielleicht hat Stevin sich da gedacht: ich lasse bei den Potenzen die ewig gleiche Basis 10 weg

    („das weiß ja jeder, dass wir uns im Zehnersystem bewegen“)


    • ergibt oder endlich kurz

    . = .

    Dabei sind Stevin allerdings auch die Minuszeichen abhanden gekommen, wofür es zwei Gründe geben mag: