 ),
),warum Mathematiker es so mit Dreiecken haben
Ich bin mir ja für Veranschaulichung zu (fast) nichts zu schade.
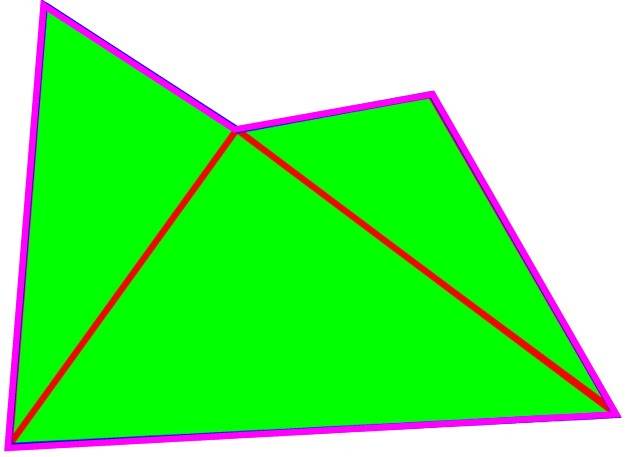
Alle Vielecke (ebenen Figuren mit geraden Rändern) lassen sich in Dreiecke unterteilen
(z.B.  ),
),
woraus folgt: wenn man mit Dreiecken (Geometrie!) rechnen (Algebra!) kann
(Flächenberechnung, Winkelsumme, Satzgruppe des Pythagoras, Trigonometrie),
kann man auch alle anderen Vielecke berechnen - und muss sich nicht für jedes Vieleck
(unendlich viele Vieleck-Arten!)
jeweils eine extra Formel merken.

... wobei natürlich zu beachten ist, dass die meisten Mathematiker nach wie vor MathematikER, also Männer sind - vielleicht eben wegen der Faszination für solche Dreicke:

Aus dieser Art von Dreiecken lässt sich aber durchaus auch mathematisch etwas lernen:
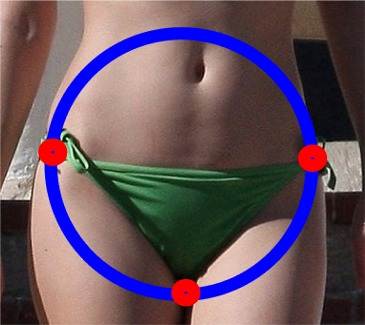

(Man könnte also
sprechen.)
Bzw. dreidimensional
 ,
,
womit wir in der sphärischen (= Kugel-)Geometrie sind - und beispielsweise die Winkelsumme des Dreiecks größer als 1800 ist.
(Männer hingegen sind rechteckig  - und tragen sehr viel mehr Tuch.
- und tragen sehr viel mehr Tuch.
Nun hat jedes Rechteck zwar immerhin einen Um-, aber [außer Quadraten] keinen Inkreis - was mir weniger "harmonisch" erscheint.)
| PS: |
Dieses Plakat wurde von vielen Feministinnen (wobei "Feministin" für mich ein Ehrentitel ist!) als sexistisch angesehen. Das mag ja stimmen, nur: ist es frauen- oder männerfeindlich?
|
| PPS: |
 |
| PPPS: |  |