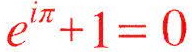
die schönste Gleichung der Welt: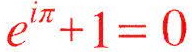

("Goat")

Vgl.

An der Gleichung 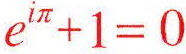lässt sich auch für Laien (Schüler) immerhin ansatzweise (vgl. PS) zeigen, weshalb sie von Mathematiker oft als „schönste Gleichung der Welt bzw. aller Zeiten“ gehandelt wird - und was Mathematiker überhaupt an Gleichungen schön finden.

Schön an der Gleichung e ^{i π} + 1 = 0 ist 

• natürlich nicht die äußere, optische Verpackung

(wenn es danach ginge, könnte da genauso gut f ^{k ρ} + 3 = 5  stehen),

• sondern die „Denkwelt“, die hinter der Gleichung e ^{i π} + 1 = 0 steckt:

• die Zahlen 1 und 0:

Das ist zwar kürzer, aber dabei sind

• die einfachste Zahl 1 zugunsten der schon ein wenig schwierigeren negativen Zahl - 1

• und die scheinbar überflüssige, in der Mathematik aber so bedeutsame Zahl 0

verschwunden.

• die Zahl π :
  

Von der  Gleichung e ^{i π} + 1 = 0 wird Laien vermutlich zumindest noch die "Kreiszahl" π ≈ 3,14 ansatzweise bekannt sein.

Wenn aber die 1, die 0 und π bedeutsame Zahlen sind, lässt sich schon vermuten, dass auch e und i solche bedeutsamen Zahlen sind.

• die Zahl e :

Nun ist bei π mit 3,14 und bei e mit 2,71 noch lange nicht das Ende der Fahnenstange erreicht, sondern wenn wir die Dezimalschreibweisen beider Zahlen auf hundert Nachkommastellen genau anschauen, erhalten wir

• π ≈ 3,1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679

• e ≈ 2,7182818284590452353602874713526624977572470936999595749669676277240766303535475945713821785251664274

Das ist bei beiden Zahlen schon ein fieser Rattenschwanz, denn da ist keine Regel (Periode) erkennbar, und somit gibt es bis dahin keine Möglichkeit, die Zahlen in Dezimalschreibweise exakt, aber kürzer aufzuschreiben.

Aber es kommt noch schlimmer

(bzw. für Mathematiker schöner):

es lässt sich zeigen, dass sowohl bei π als such bei e in den Dezimaldarstellungen

• unendlich viele Nachkommastellen vorkommen

• und keine Perioden.

Solche Zahlen mit unendlich vielen nicht-periodischen Nachkommastellen nennt man

(im Gegensatz zu den „rationalen“ Zahlen, die

• in Dezimalschreibweise entweder endlich oder periodisch hinter dem Komma sind
• und deshalb auch als Brüche aus ganzen Zahlen geschrieben werden können)

„irrationale“ Zahlen.

(Nebenbei [das wird unten noch wichtig]: rationale und irrationale Zahlen zusammen ergeben zusammen die "reellen" Zahlen, und diese füllen den Zahlenstrahl komplett aus, d.h. es gibt auf ihm keine Lücken mehr:

)

Irrationale Zahlen kann man nie vollständig aufschreiben, und weil jede Abkürzung nur ungenau ist, machen die Mathematiker aus der Not eine Tugend, benutzen sie nämlich der Einfachheit halber nur die beiden kurzen Buchstaben π und e.

(Wenn eh alles aussichtslos ist: warum kompliziert, wenn's auch einfach geht?) 

Die Zahl e ist sowohl innermathematisch als auch bei Anwendungen von fundamentaler Bedeutung:

• z.B. ist die Exponentialfunktion f(x) = e^x die einzige Funktion, deren Ableitung ganz einfach wieder e^x  ist, also f ‘ (x) = e^x .

Hier sieht man eine Gemeinsamkeit mit der Kreiszahl π : wenn man ein Problem

(Kreisumfang und -fläche bzw. Ableitung)

sehr einfach lösen will, handelt man sich dabei als „Kollateralschaden“ manchmal sehr schwierige Zahlen ( π bzw. e) ein.

• Die Zahl e taucht immer wieder auf, wenn man Wachstumsprozesse und Zufallsereignisse beschreiben möchte.

Bleibt zuguterletzt noch

• die Zahl i :

Aber es gibt halt Leute, die, wenn sie die Erdoberfläche abgegrast haben, auch noch die Ozeane oder den Weltraum entdecken wollen, und da die reinen Mathematiker auf die Widrigkeiten der Außenwelt pfeifen, denken sie oftmals:

1. : „Ich mach mir die Welt / widewide wie sie mir gefällt“: wenn der Zahlenstrahl abgegrast ist, nutzen die Mathematiker eben die „terra incognita“ (unbekannte Welt)   neben dem Zahlenstrahl:

2. "Zwei mal drei macht vier / und drei macht neune": so wie Pipi Langstrumpf sich neue Rechenregeln definiert

(die anfangs zum falschen Zwischenergebnis 4, am Ende aber doch wundersam zum richtigen Ergebnis 9 führen),

definieren sich auch die Mathematiker für die neue Zahl eine neue Rechenregel, nämlich i • i = -1 bzw. i ² = -1 :

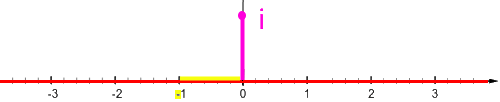
Bemerkenswert ist es aber insbesondere, dass die so harmlos daherkommende Gleichung i ² = -1 in Wirklichkeit eine ist. Da wird den Schülern in der Schule immer zweierlei eingebläut: 

1. : wegen - • - = + und + • + = + ist das Quadrat

• sowohl einer negativen Zahl
• als auch einer positiven Zahl

immer positiv, d.h. a ² = -1 ist unmöglich.

Was Schüler in der Schule allerdings nicht erfahren, ist, dass

• a ² = -1 nur für die in Schulen meist nur durchgenommenen Zahlen auf dem Zahlenstrahl unmöglich ist,

• während  i ² = -1 für die neben dem Zahlenstrahl liegende Zahl i sehr wohl funktioniert

(weil die Mathematiker es sich einfach tolldreist so definiert haben;

wobei ergänzt werden muss, dass die Motivation der Mathematiker, Zahlen neben dem Zahlenstrahl zu betrachten, nicht einfach nur darin begründet lag, dass sie einfach nur aus Jux auch mal neben dem Zahlenstrahl spielen wollten, sondern dass es dafür durchaus aus auch handfeste innermathematische Gründe gab, die hier aber nicht weiter betrachtet werden).

2. : "die Wurzel aus einer negativen Zahl ziehen" ist fast so eine  schlimme mathematische Todsünde wie "durch Null teilen".

Aus i ² = -1 könnte man nun aber nicht ganz korrekt folgern. Auch das gilt jedoch nur für die Zahl i  neben dem Zahlenstrahl, nicht für die reellen Zahlen auf dem Zahlenstrahl.

Man nennt i auch eine "imaginäre" Zahl, wobei "imaginär" wohl "eingebildet" bedeutet, aber nicht im Sinne von "arrogant, überheblich", sondern im Sinne von "mit großer Phantasie erdacht".

Mit i wurde die wunderbare Welt der "komplexen" Zahlen (aller Zahlen neben dem Zahlenstrahl) erschaffen, die sowohl innermathematisch als auch bei Anwendungen eine große Rolle spielt.

Die "Funktionsweise" von i und der komplexen Zahlen soll hier nicht erklärt werden, sondern es reicht hier: "Schön zu wissen, dass es diese Zahlen gibt."

Bislang haben wir also erfahren:

abgesehen von + und = kommen in der Gleichung e ^{i π} + 1 = 0 trotz der Verwendung der Buchstaben e, i und π nur Zahlen vor. Die Gleichung e ^{i π} + 1 = 0  ist also eine hundsgewöhnliche Rechnung

(man addiere

• die scheinbar teuflische Zahl e ^{i π}
• und die einfache Zahl 1

und erhält dann die einfache Zahl 0 ).

Kommen wir aber nochmal zurück zur Gleichung e ^{i π} = - 1 . Sie besagt schlicht und einfach, dass

• das atemberaubende Jonglieren e ^{i π} mit den wirklich schwierigen Zahlen e, i und π

• erstaunlicherweise zu dem ganz simplen Ergebnis - 1 führt!

Wie kommt es aber, dass die völlig unterschiedlichen und hochkomplizierten Zahlen e, i und π sich derart schön (!) zur simplen - 1 zusammenfügen?:

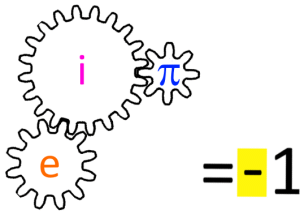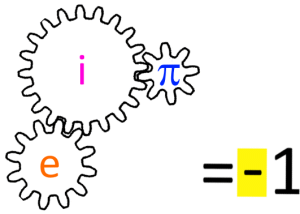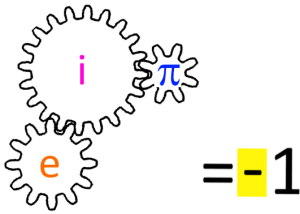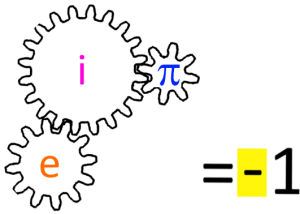
(Je fremdartiger die Zahl, desto größer ist das Zahnrad und desto mehr Zähne hat es somit.)

(Hier sei nicht erklärt, warum e ^{i π} = - 1 gilt

[wer ein bisschen Englisch kann, erfährt es hier:   ]

Immerhin erwähnt sei aber, wer dieses wunderbare Ergebnis entdeckt hat: verweist schon darauf, dass es der Mathematikgigant

Leonard Euler
(1707 - 1783)

war.

Und nebenbei: auch der Beweis ist schön.)

Schön an der Gleichung e ^{i π} + 1 = 0 ist

1. , dass sie trotz der drei komplizierten Zahlen e, i und π und insbesondere von e ^{i π}  so kurz ist;

2. , dass in ihr die fünf völlig unterschiedlichen fundamentalen Zahlen  e, i, π, 1 und 0 und damit völlig unterschiedliche mathematische Teilgebiete in Beziehung gesetzt werden,

3. also, dass die Gleichung so überaus produktiv für die Gesamtmathematik war und eine ganz neue "Denkwelt" eröffnet hat!

Fast möchte man fragen: woher wussten die drei so unterschiedlichen Zahlen e, i und π, dass sie letztlich doch so wundersam zusammenpassen?

PS:

man dürfe im Unterricht doch nicht so halb durchnehmen, also ohne genaue Kenntnisse von e und i , den Beweis von von? Doch, sowas darf, ja muss man bei einigen Themen ab und zu! Vgl. . Das schließt ja nicht aus, sondern fordert geradezu dazu auf, dass man z.B. eben doch mal ansatzweise in die komplexen Zahlen einsteigt.