fahrlässige Klassenarbeiten

Ich bin ja immer vorsichtig mit Lehrerkritik:

1. weil ich größtes Verständnis für die ungünstigen Umstände habe, die zu Fehlern führen:

• das ist keine süffisante Pseudo-Entschuldigung, aber eine Erklärung: "wo gehobelt wird, fallen Späne",
• Stress, der verlässlich zu Fehlern führt,
• in der Mathematik: Rechenfehler des Lehrers, die er trotz mehrfacher Kontrolle nicht bemerkt

(man ist ja vor allem blind für die eigenen Fehler, und einmal [falsch] Niedergeschriebenes wirkt enorm suggestiv);

2. : "wer ohne Sünde ist, werfe den ersten Stein": ich habe doch oft genug selbst Fehler gemacht.

Ein Standardfehler von Lehrern (!) in Klassenarbeiten

(also ein Fehler, den die Schüler [!] ausbaden müssen)

ist eine

(für die Schüler)

allzu umständliche oder unklare Aufgabenstellung: man ist als Lehrer derart im Stoff und der Fachsprache "drin", dass man diesen Fehler oft gar nicht mehr bemerkt

(immerhin sollte man nach Jahren der Berufstätigkeit aber die meisten Schülerprobleme

[auch beim Aufgabenverständnis]

halbwegs kennen und deshalb "benutzerfreundlicher" formulieren können).

Bzw. wenn man überhaupt halbwegs selbstkritisch ist

(wobei es natürlich viel einfacher ist, wenn man alles auf die ach so dumme "Jugend von heute" schiebt),

bemerkt man den eigenen Fehler oftmals erst nach der Klassenarbeit, wenn also das Kind bereits in den Brunnen gefallen ist, d.h. viele Schüler eine Aufgabe nicht oder nur falsch haben bearbeiten konnten.

(Und dann ist man - finde ich - verpflichtet, die Bepunktung der Aufgaben nachträglich zu ändern; einer der vielen geradezu antipädagogischen Nachteile zentraler Prüfungen ist es aber, dass man da die Bewertung nicht nachträglich ändern kann / darf.

Genau genommen muss man die Bepunktung dann ändern, wenn man merkt, dass man selbst dem "Versagen" der Schüler Vorschub geleistet hat.)

Ein guter Tipp beim Lehrerfehler "umständliche oder unklare Aufgabenstellung" ist es, die geplante Aufgabenstellung vorweg einem absoluten Laien

(z.B. der Ehefrau)

vorzulegen und dann zu beobachten, welche Hilfen nötig sind, damit der Laie den Aufgabentext versteht.

Drei Beispiele aus verschiedenen Klassenarbeiten

(die andere Lehrer gestellt haben, also nicht ich selbst):

1. : die Schüler sollen

1. aus

• den Schnittpunkt S der beiden Geraden,
• die Gleichungen der beiden Geraden

ablesen,

2. aus den beiden derart ermittelten Geradengleichungen den Schnittpunkt S berechnen.

Zeichnungen haben

• den Vorteil, anschaulich zu sein,
• aber auch den Nachteil, nie ganz genau (ablesbar) zu sein

(das ist insbesondere ein Problem, wenn die Koordinatenachsen - wie im vorliegenden Fall - nur mit ganzen Zahlen versehen sind, wichtige Koordinaten aber "krumm" sind).

Dieser Nachteil ist ja der Grund dafür, dann doch zu rechnen, um exakte Ergebnisse zu erhalten

(eine Exaktheit, die vielen Nicht-Mathematikern maßlos übertrieben erscheint).

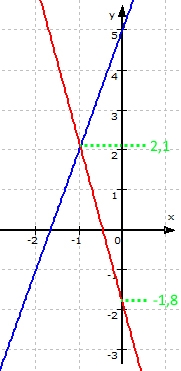
Im vorliegenden Fall scheint der Schnittpunkt S die x-Koordinate -1 zu haben, und die y-Koordinate ist ungefähr (!) 2,1, womit sich insgesamt S ( -1 | 2,1 ) ergibt.

Mit den beiden ebenfalls aus der Zeichnung abgelesenen Geradengleichungen y = 2,9x + 5 und y = - 3,9x - 1,8 ergibt sich für den Schnittpunkt S  rechnerisch ebenfalls S ( -1 | 2,1 ), d.h. wir haben sowohl den Schnittpunkt S als auch die beiden Geradengleichungen erstaunlich gut aus der Zeichnung abgelesen.

Der Lehrer, der die Aufgabe gestellt hatte, hat aber weder den aus der Zeichnung abgelesenen noch den berechneten Schnittpunkt S ( -1 | 2,1 ) akzeptiert, sondern hielt

(sowohl beim Ablesen aus der Zeichnung als auch bei der Rechnung)

einzig und allein den Schnittpunkt S ( -1 | 2 ) für korrekt.

Wie konnte das passieren? Ich vermute mal, dass der Lehrer versehentlich (!) ungenau gezeichnet und in Wirklichkeit Folgendes gemeint hat:

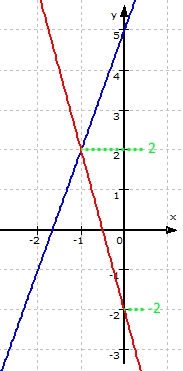
Damit ergeben sich durch Ablesen aus der Zeichnung S ( -1 | 2 ) sowie die beiden Geradengleichungen y = 3x + 5 und y = - 4x - 2 und daraus auch rechnerisch S ( -1 | 2 ).

Die Aufgabe war also einfacher gemeint, als sie durch die ungenaue Zeichnung wurde.

Dass eine Zeichnung versehentlich ungenau ausfällt, mache ich keinem Lehrer zum Vorwurf. Nur sollte ein Lehrer natürlich seine Bewertung nachträglich den (versehentlichen) Tatsachen anpassen, also S ( -1 | 2,1) als richtige Lösung akzeptieren.

Es ist sogar noch komplizierter: die Rechnungen für S ( -1 | 2,1) sind

(wenn auch nur minimal)

schwieriger als die für den eigentlich gemeinten Schnittpunkt S ( - 1 | 2 ), weshalb die Schüler dafür mehr Zeit brauchen, als der Lehrer ursprünglich geplant hat

(und noch schwieriger konnte es werden, wenn ein Schüler andere Näherungswerte für den Schnittpunkt und die Geraden abgelesen hat):

Zeit, die den Schülern eventuell später für nachfolgende Aufgaben gefehlt hat. Das könnte bedeuten, dass der Lehrer wegen einer versehentlich ungenauen Aufgabe die Bewertung der ganzen Klassenarbeit ändern müsste.

(Ich habe mal in einer Abitur-Vorklausur versehentlich

[und trotz mehrfachen Korrekturlesens]

in der zentralen Aufgabe einen Vorzeichenfehler gemacht, der zur Folge hatte, dass der einzige Prüfling, ein ansonsten wirklich "guter" Schüler, sich um Kopf und Kragen gerechnet und daher große Teile der Klausur nicht mehr geschafft hat.

[Ich konnte während der Klausur nicht anwesend sein und somit auch nicht auf eine eventuelle Rückmeldung des Schülers reagieren.]

Da muss man als Lehrer doch im Nachhinein höchst flexibel reagieren [dürfen].)

Fragt sich nur, ob der Lehrer seinen Fehler (die zeichnerische Ungenauigkeit) überhaupt bemerkt hat: er hat ja S (-1 | 2) gemeint und sieht daher S ( - 1 | 2,1) als falsch an. Und gerade diejenigen Schüler, die nicht genau gemessen, also auch S ( -1 | 2 ) erhalten haben, bestätigen den Lehrer ja noch in seinem Irrtum.

Vorwerfen kann man dem Lehrer dann nur, dass er nichtmal für die richtige Rechnung mit vermeintlich falsch abgelesenen Werten Punkte vergeben, sondern alles als falsch angesehen hat

(ein Fehler, der leicht unterläuft, wenn ein Lehrer aus Zeitmangel, Faulheit oder mathematischem Fundamentalismus

["es zählt nur, was absolut richtig ist"]

nicht die Rechnungen, sondern nur die Ergebnisse anschaut und bewertet).

2. : weil ich das Originalblatt der Klassenarbeit, aus der die Aufgabe in 1. stammt, nicht mehr finden konnte, habe ich die Zeichnungen sinngemäß neu erstellt.

In Wirklichkeit war die Originalzeichnung sehr undeutlich ausgedruckt und offenbar eine schlechte Kopie einer Kopie einer Kopie

(vermutlich aus einer Klassenarbeit, die der Lehrer schon  mal Jahre vorher gestellt hatte).

Nunja, einiges war in der guten (?) alten Zeit vielleicht auch besser: im Zeitalter der mild duftenden (:-) Spiritusmatrizen

war es noch kaum möglich, uralte Arbeitsblätter andauernd für neue Schulstunden und Klassenarbeiten zu recyceln

(manchmal verraten sich Lehrer heutzutage dadurch, dass sie [versehentlich?] nicht mal das alte Datum durch das neue Datum ersetzen;

und überhaupt: heutzutage ertrinken die Schüler ja geradezu in einer Sintflut von Kopien

[Standardfrage an den Lehrer: "Können Sie die Kopien demnächst bitte vorher lochen?", "Denn was man schwarz auf weiß besitzt, kann man gestrost nach Hause tragen" und abheften - und vergessen],

ja, ihre ganze Schulzeit besteht weitgehend aus Kopien, Kopien, Kopien; da müssen sie ja fast den Eindruck gewinnen, dass das ganze Leben oder zumindest alle Wissenschaft nur eine Kopie ist: ein Eindruck, den sie allerdings vermutlich sowieso schon haben, da sie andauernd fremde Erkenntnisse wiederkäuen müssen, statt mal eigene haben zu dürfen).

Ein schönes (mir aber leider nicht mehr vorliegendes) Beispiel für das Kopierunwesen war eine Matheaufgabe, bei der die Schüler (mittels Mittelsenkrechten) den Punkt ermitteln sollten, der gleich weit von einer Kirche, einer Schule und einem Bahnhof entfernt war. Allerdings war die Kirche auf der beiliegenden schlecht kopierten Skizze gar nicht zu erkennen!

3. : bei 1. und 2. handelte es sich um rein formale Fahrlässigkeiten. Beim nun folgenden Beispiel ist aber die abgeprüfte Mathematik selbst das Problem:

in einer Klassenarbeit über Gleichungssysteme wurde erst eine Aufgabe gestellt, bei der einfache Brüche rauskamen

(ich hätte ja zu Anfang erstmal eine Aufgabe gestellt, bei der ganze Zahlen rauskommen, denn schließlich ist das abgeprüfte Thema in erster Linie "Gleichungssysteme" und sind Brüche höchstens ein Nebeneffekt).

Auf die erste Aufgabe folgte dann als zweite Aufgabe:

            24x + 15 = 22y
         - 10y - 24x = 4 

Offensichtlich bestand der Sinn dieser Aufgabe darin, die Schüler - böse gesagt - dadurch reinzulegen, dass

• in der ersten Gleichung die Terme mit x und y nicht (wie sonst üblich) beide auf der linken Seite der Gleichung stehen,
• in der zweiten Gleichung nicht die übliche Reihenfolge "erst der Term mit x, dann der mit y" eingehalten wurde.

Wenn sich die Schüler dadurch nicht haben reinlegen lassen, erhalten sie (hoffentlich) erst das (richtige!) Ergebnis y = .

Der psychologische Effekt wird da wohl bei den meisten Schülern "das kann nicht stimmen" sein. Und dann rechnen sie eventuell nochmal nach - und verlieren viel Zeit.

Wenn sie später y = z.B. in die erste Gleichung 24x + 15 = 22y einsetzen, erhalten sie eventuell das (richtige!) nicht weiter kürzbare Ergebnis x = 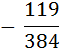, womit die Verwirrung wohl endgültig perfekt ist.

(Da die Ergebnisse y = und x = 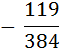auch in meinen Augen zweifelhaft wirkten, habe ich für das Lösen des Gleichungssystems samt Probe in beiden Anfangsgleichungen drei Seiten gebraucht!)

Da stellt sich doch die Frage, warum ein Lehrer solch eine Aufgabe stellt. Reicht es nicht, die o.g. Schwierigkeiten

("falsche" Anordnung der x- und y-Terme)

einzubauen, oder muss "man" das noch zusätzlich mit schwierigen Brüchen verzieren

(obwohl doch die Beherrschung der Brüche schon in der ersten Aufgabe abgeprüft worden war)?

Ist das ein Versehen bzw. gar grobe Fahrlässigkeit des Lehrers

(vielleicht einfach, weil er die Aufgabe vorher gar nicht durchgerechnet bzw. anhand eines Lösungsbuchs überprüft hat)

oder steckt dahinter die Absicht, möglichst schikanöse Klassenarbeiten zu stellen?

(Ich bin ja großer Anhänger von Brüchen, die letztlich viel einfacher als Dezimalzahlen sind, und sowieso dafür, dass alter Schulstoff auch in neuen Zusammenhängen wieder auftaucht. Außerdem müssen die Schüler natürlich lernen, dass sogar einfache Anfangsgleichungen zu schwierigen Ergebnissen führen können

[und umgekehrt schwierige Anfangsgleichungen zu einfachen Ergebnissen],

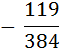ja, dass auch in der Mathematik nicht alles glatt aufgeht. Aber eine Aufgabe mit den Lösungen y = und x = hätte ich niemals in einer Klassenarbeit gestellt, allemal jedoch im Unterricht.)