"[...] mittlerweile gibt es verbesserte humane menschliche Arbeitsbedingungen am Fließband.
Es gibt - bunte Schraubenzieher."


"Alles so schön bunt hier."

Der faux pas hat mich doch schwer gefuchst:

        ein, wobei

Man mag solch eine inkonsequente Benutzung der Farbe Blau für nebensächlich halten, ja sogar meinen, dass die Schüler gar nicht früh genug lernen könnten, dass

           (sonst sind sie völlig hilflos, wenn die mathematische Gleichung y = • 10 x2 in der Physik [beim freien Fall] so daher kommt:
 s = g t2 ),

Mich stört da allerdings das "gar nicht früh genug", das sich für mich gefährlich nach "früh krümmt sich, was ein Häkchen werden will [?]" anhört.

Die Anfangsgründe der Achsen- und Punktspiegelung werden ja - wohlgemerkt! - in der 5. Klasse durchgenommen, also mit zehnjährigen Kindern.

 

Ich war ja immer unbedingter Vertreter der "Anti-These", dass ein Lehrer nicht eigene Kinder "haben" muss, um Schüler zu verstehen:

  • ich kenne Lehrer, die keine Kinder und "dennoch" größtes Verständnis für Freud, Leid und altersspezifische Lernprozesse von Kindern/Jugendlichen haben;

  • und umgekehrt kenne ich Lehrer, die zuhause einen ganz Stall voller Kinder haben und dennoch (ohne Anführungszeichen!) völlig verständnislos gegenüber Schülern sind

(das sind nebenbei jene Lehrer, die, selbst von keinerlei Zweifel geplagt, Kinder erziehen, die ebenfalls niemals von Zweifeln geplagt werden und sogar - geradezu beneidenswert - in der "Pubertät" bestens funktionieren):

"man muss die Tollkirsche nicht gegessen haben, um zu wissen, dass sie giftig ist", d.h. man muss nicht alles (direkt) erlebt haben, um mitreden zu können, sondern es reichen Aufmerksamkeit für die Probleme anderer und ein wenig soziale und emotionale Phantasie.

(Ein Beispiel: ich kann von einem "Nebenfach"-Lehrer verlangen, dass er

[ohne schlechtes Gewissen]

die unerträgliche Korrekturbelastung von "Hauptfach"-Lehrern wahr- und "ernst" nimmt: wenn man unbedingt will, kann man das auch modisch mit den "Spiegelneuronen" bzw. dem EQ erklären.)

Als Vater/Mutter eines Kindes sieht man "alles" aber doch noch mal ganz anders:

  • einerseits: bevor ich Vater wurde, habe ich mir immer Mühe gegeben, in fünften Klassen "kindlich" zu unterrichten;

nehmen wir als Beispiel nur mal das Bedürfnis vieler Kinder, ellenlang Erlebnisse zu erzählen;

spätestens dann, wenn mehrere Kinder nacheinander ihr gesamtes Wochenende erzählen wollen, wird "man" als Lehrer ungeduldig, da

  • die Erzählungen vielleicht noch assoziativ am jeweils gerade anliegen Unterrichtsstoff ansetzen, aber verlässlich immer weiter von ihm wegführen, je länger sie dauern;

  • die Erzählungen oftmals nur ihre Erzähler, kaum aber den Rest der Klasse interessieren

(was man am besten daran erkennt, wie viele Schüler unermüdlich aufzeigend darauf hinweisen, dass sie auch noch halbe Romane erzählen wollen);

  • die Schüler kein Ende finden

(man will die kindliche Phantasie ja auch nicht abwürgen)

  • und man somit schnell eine ganze Stunde verliert und somit den vorgegebenen Lehrplan nicht schafft

(fragt sich nur, ob "man" summa summarum wirklich was verliert, denn dass die Kinder Geschichten erzählen, ist ja durchaus auch ein Gewinn);

  • andererseits merke ich erst jetzt, wo ich einen Sohn in einer 5. Klasse habe, dass die Fünftklässler noch viel kindlicher sind, als ich immer gedacht habe - und dass der lehrplangemäße Schulstoff

(z.B. in Erdkunde die Koordinaten von Orten auf dem Globus bzw. im Atlas)

nicht nur Kilometer, sondern sogar Lichtjahre vom "Leben" Zehnjähriger entfernt ist

(aber vielleicht ist die Eltern-Perspektive sogar besonders "falsch": weil sie die Kinder von Geburt an groß(!) gezogen haben, sehen sie sogar in ihren erwachsenen Kindern (!) immer noch kleine (!) Kinder).

Ich meine also, dass man bei Fünftklässlern erst sehr langsam in die Formalisierung und Abstraktion aufsteigen sollte - und dass die Zehnjährigen sowieso klare Strukturen wie z.B. Klassenarbeitshefte brauchen, die pro Fach eine spezielle Farbe (!) haben

(z.B. Deutsch = rot, Mathe = blau ...).

Überhaupt kommt Farbigkeit dem offensichtlichen Bedürfnis vieler Fünftklässler

(vor allem FünftklässlerINNEN?!)

entgegen, alles hübsch bunt an- und auszumalen.

Und da ist es doch ein gewaltiger Unterschied, ob man nur die Seitenstrecken oder auch die Flächen bunt anmalt:

    

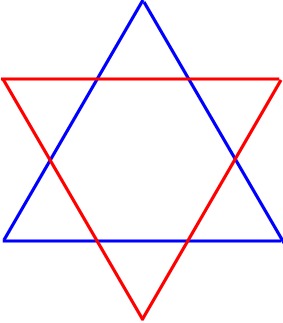
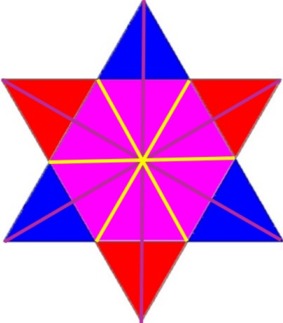
(das jeweils zweite Dreieck geht aus dem ersten durch Punktspiegelung am Mittelpunkt des ersten hervor)

Wer eine geometrische Figur derart bunt wie im rechten Bild ausmalt, zeigt

(vgl. das Ausmalen von


Mandalas,

das 

überhaupt scheint mir das Erkennen von

viel wichtiger zu sein als das ewige Konstruieren

[puristisch mit Zirkel und Lineal]

im üblichen Geometrieunterricht);

immerhin ist der Mensch u.a. ein mustererkennendes Wesen und die Mathematik u.a. eine "Mustererkennungswissenschaft";

hier sei nebenbei auch schon auf die sinnvolle Verwendung von Farben hingewiesen:

sind natürlich in der Mischfarbe von rot und blau, also lila gehalten.)

Es ist schon viel getan, wenn die Mathematik überhaupt bunt wird

  ,

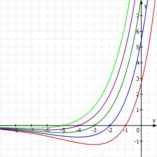statt immer nur abgenagt schwarzweiß

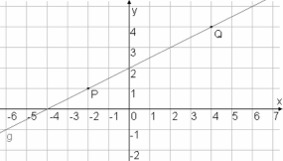
zu bleiben:

"Richtige" Mathematiker benutzen Farben hingegen höchstens, um etwa bei komplexeren geometrischen Konstruktionen verschiedene, sich eventuell sogar überschneidende Zwischenzustände unterscheiden zu können. Aber dann malen (?; wohl eher seriös: zeichnen) sie höchstens die Seiten solcher Figuren, nicht aber deren Flächen bunt. Streng ihrem Prinzip "nur so viel wie nötig, aber keinen Handschlag mehr" folgend, werden sie das Ausmalen von Flächen als unnötig und damit nachgerade "unmathematisch" empfinden.

Es ist ja tatsächlich ein Problem: wenn Fünftklässlerinnen erst mal mit dem millimetergenauen Ausmalen beginnen, kann man den Rest der Schulstunde vergessen. Da man(n) als Mathelehrer für solch weitschweifiges Ausmalen kein Verständnis hat, vor allem aber, weil der Stoffdruck des Lehrplans gnadenlos ist, würgt man freundlich, aber schnell das Ausmal-Bedürfnis ab -  und raubt somit vor allem

(Vorsicht, Sexismus!?)

Mädchen ihren ästhetischen Zugang zur Mathematik

        (ich glaube fest, dass die Mathematik für alle "richtigen" Mathematiker ein ästhetisches Spiel ist, aber da ist meistens eine "innere" Ästhetik gemeint, nämlich z.B. die Schönheit ["Eleganz", Ideenreichtum] von Beweisen).

Farbigkeit steht schnell im Ruf von

(überflüssigem, wenn nicht gar ablenkendem)

"Deko" und Schnickschnack.

Ich habe ja selbst an anderer Stelle geschrieben, dass sich das Handwerkszeug von Mathematikern auf Zirkel, Lineal und Bleistift bzw. Tafel und (weiße) Kreide beschränkt

(die "eigentliche" Mathematik

[z.B. die platonische Welt perfekter Kreise und Kugeln]

existiere sowieso nur im Kopf, und Schriftliches diene da nur als Gedächtnisstütze und zur Kommunikation mit anderen).

Beim Handwerkszeug habe ich aber nicht von Buntstiften geredet, ja, ein Mathematiker mit einem Buntstiftkästchen unterm Arm kommt einem geradezu unmathematisch = (?) unmännlich vor.

Von wegen "Deko und Schnickschnack": aufgrund neuer drucktechnischer Möglichkeiten sind inzwischen sogar die Mathe-Schulbücher bunt. Sinnvoll ist das bei geometrischen Zeichnungen, ansonsten wird Farbe in diesen Schulbüchern aber nur für nette Bildchen, also Dekorationen benutzt. Im Vergleich mit den (Schwarzweiß-)Bleiwüsten alter Schulbücher hat sich also wenig geändert

  ,

und deshalb kommen mir die neuen Schulbücher vor wie jene Reklame, in der der ewig gleiche Inhalt in neuen Verpackungen beworben wird:

 

(Überhaupt stelle ich mir das Leben eines Schulbuchredakteurs gar schröcklich vor: weil ja alle fünf Minuten neue Schulbücher erscheinen

[damit die Verlage immer gut verdienen],

muss er permanent und unter enormem Zeitdruck scheinbar Neues, also ewig Altes produzieren.)

Aber sogar im Bereich der Geometrie ist noch sehr viel mehr möglich, wie ein gewisser Oliver Byrne  schon im Jahr  1847 (!) ziemlich radikal bewiesen hat:


(jetzt neu in Faksimile erschienen)

Was die Verlage aber überhaupt noch nicht begriffen haben und auch im Unterricht kaum vorkommt

(was also meine niegelnagelneue Farbenlehre ist),

ist die systematische Verwendung von Farben auch

Das Lösen von Gleichungen hat immer das Ziel, dass in der letzten Zeile nur noch x bzw. EIN x steht

(wir wollen halt nie wissen, was z.B. 17 Mercedes kosten

[eine völlig abstrakte Zahl],

sondern immer, was EIN Mercedes kostet).

Das Lösen von Gleichungen sieht also immer so aus:

Irgendwas mit x = was  anderes

                 ...                =          ...                             

                 ...                =          ...

                                x  =     Lösung.

          zunehmende Isolierung von x

(Man könnte also auch sagen, dass x immer mehr aller zwischenmenschlichen Kontakte beraubt und in Isolationsfolter überführt wird:

              

                       ↓

            

             ↓

  

Nebenbei: die letzte Zeile sieht bei quadratischen Gleichungen immer so aus:

   )

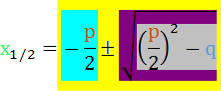Ein konkretes Beispiel:

4x + 5 = 2x - 3

Auf dem Weg zum Standardziel x = Lösung stört da zu allererst, dass das x noch auf beiden Seiten vorkommt, was wir schell beseitigen

       4x + 5 = 2x - 3 | - 2x

        2x + 5 =      - 3

Jetzt stört links noch alles außer dem nackten x, also

Wir entfernen immer zuerst, was am "weitesten" von x  entfernt ist. Da aber 2x  die Multiplikation 2•x bedeutet und die Punkt- vor der Strichrechnung kommt, ist + 5 "weiter" von x entfernt als die 2 und müssen wir zuerst dieses + 5 entfernen:

        2x + 5 =     - 3 | - 5

        2x       =     - 8

Und jetzt stört nur noch die 2 vor dem x, die als letzte beseitigt wird:

        2x      =     - 8  | : 2

           x     =     - 4

... womit das Standardziel

          x     =   Lösung

erreicht ist.

Ohne Zwischenkommentare:

4x + 5 = 2x - 3 | - 2x

        2x + 5 =      - 3 | - 5

        2x       =      - 8  | : 2

          x       =      - 4

Hier halte ich es aber für durchaus erhellend, verschiedene Farben zu verwenden:

  • x als die gesuchte Zahl schreiben wir in grün,

  • alles, was stört, in rot

  • und die Lösung

(also das, was sich von Anfang an hinter x verborgen hat)

in gelb:

4x + 5 = 2x - 3 | - 2x

         2x + 5 =      - 3 | - 5

         2x       =      - 8 | : 2

           x       =      - 4

Insbesondere muss also die letzte Zeile immer so aussehen:

           x =       Lösung .

---

Farben sind aber "nur" ein (wichtiges!) Layout-Element Hier also noch ein anderes Layout-Element, nämlich die Anordnung wie z.B. eben in

        

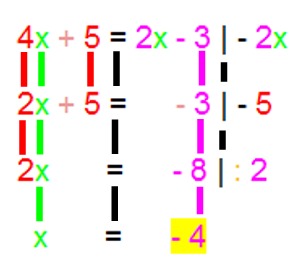
Da stehen zueinander passende Gleichungsdetails immer hübsch       

             un-
             ter-
             ein-
             an-
             der.

Das hat zwei Vorteile:

  1. wird die logische Struktur viel klarer,

  2. vergisst man dann bei Umformungen nicht so leicht Details, die längere Zeit unverändert mitgeschleppt werden müssen.

Noch deutlicher wird die Struktur, wenn man alle Zwischenschritte notiert:

                 

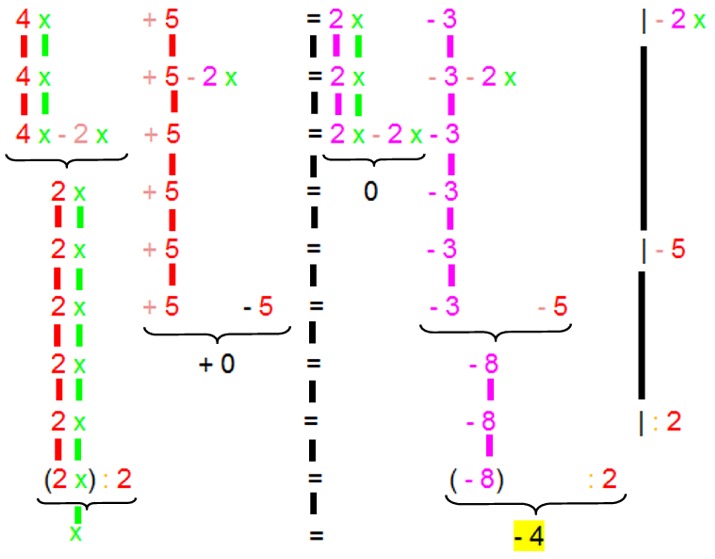
(Nebenbei: wenn das jemanden an   erinnert

[auch wenn die Gleichungslösung "top down", der U-Bahn-Plan hingegen eher konzentrisch ist],

soll's mir recht sein.)

Solch eine Schreibweise, hier mal wirklich exzessiv eingesetzt, ist sicherlich nicht immer sinnvoll, sondern nur (bzw. immerhin) dann, wenn neue Umformungsweisen gezeigt werden

(auf die Dauer darf keine

[hoffentlich längst Routine gewordene]

 Altlast vom jeweils Neuen ablenken).

Anfängern ist solch ein Untereinanderschreiben allemal zu empfehlen, wenn es auch nicht rigoros durchhaltbar ist:

man weiß ja zu Anfang einer Rechnung oftmals noch nicht, wieviel Platz man hinterher brauchen wird, um entsprechende Elemente untereinander schreiben zu können.

Für ein Schulbuch ist das allerdings kein Problem.

Noch besser finde ich es allerdings, wenn Schüler in einer Folgezeile

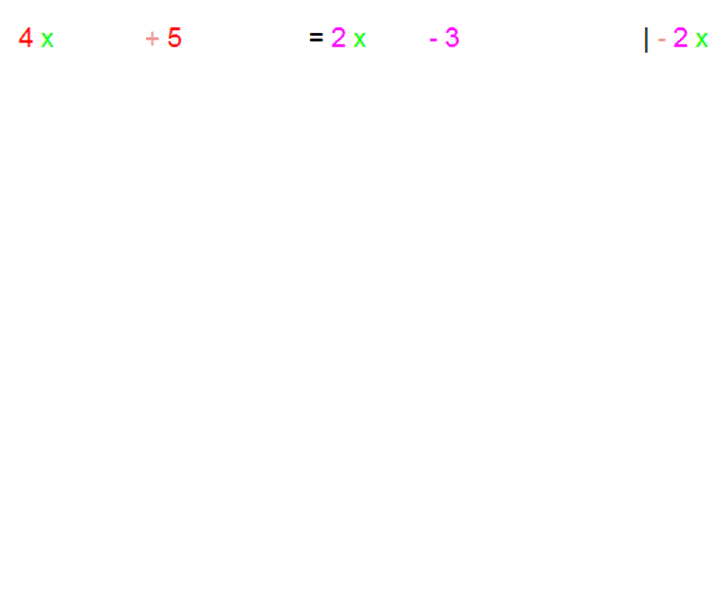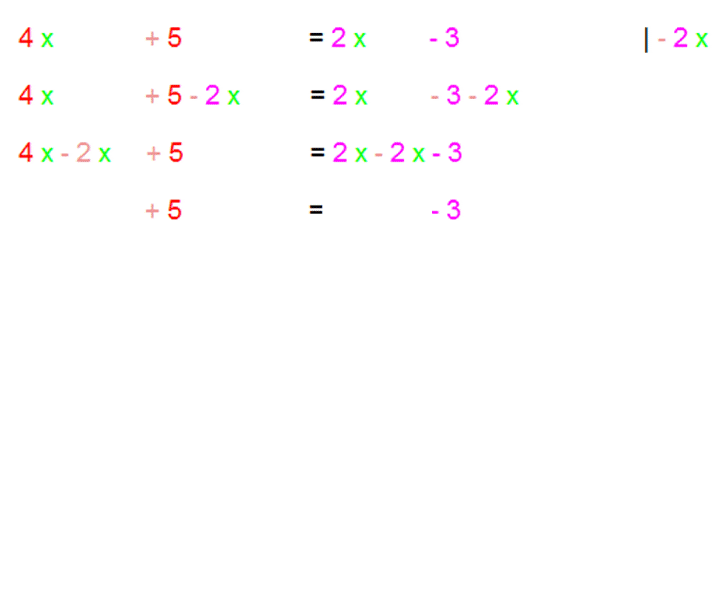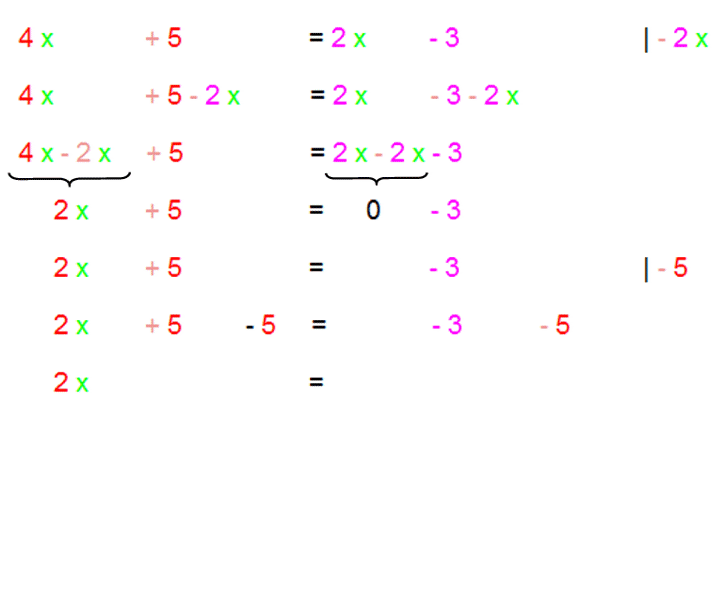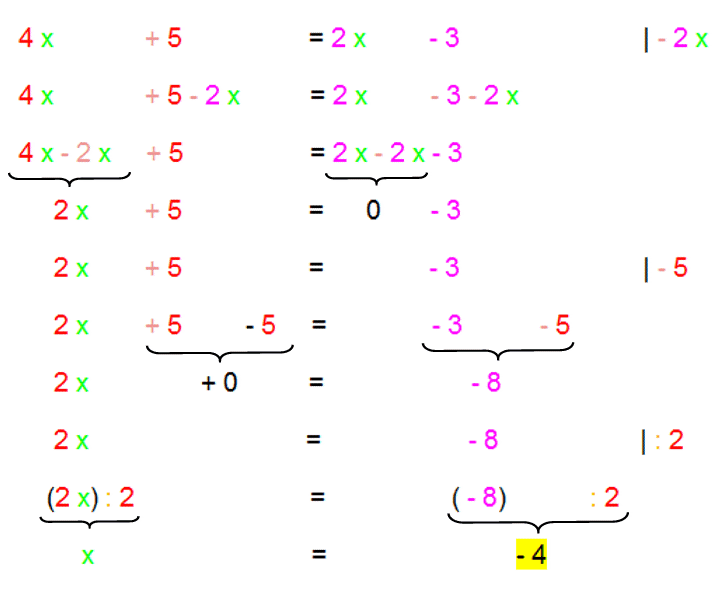
Solches Vorgehen hat mehrere Vorteile:

  1. bekommen Schüler sogar für das bloße (richtige) Abschreiben von Vorherigem Punkte,

  2. verlieren sie nicht wichtige, derzeit aber nicht anstehende Details,

  3. konzentrieren sie sich mehr auf gerade anstehende Details (immer nur eines),

  4. lassen sich ihre Rechnungen (für sie selbst!) besser nachvollziehen, wenn beispielsweise nachher ein Fehler gesucht wird: "was wollte ich eigentlich - und habe ich es denn auch wirklich getan?"

Jeder Lehrer kennt das Problem, dass viele Schüler sehr wohl Standardformeln beherrschen, aber sofort aufgeschmissen sind, wenn die Variablen mal umbenannt werden oder komplexere Terme auftauchen.

Ein Beispiel ist der "1. Binomi", also (a + b)2 = a2 + 2ab + b2, den vermutlich noch jeder Schüler runterrasseln kann

(in der Praxis wird dann allerdings liebend gerne doch das "gemischte Glied" 2ab vergessen, d.h. das Quadrat einfach nur in einer Art [falschem] Distributivgesetz auf die beiden Summanden a und b verteilt:

(a   + b  )2

  a2 + b2     )

Es reicht eben keineswegs, die binomischen Formeln nur zu kennen. Sondern man muss sie

           kennen  
      er-kennen  
  1. "anwenden"
           können.  

Zu 1., also "kennen":

in beiden Richtungen:

Zu 2., also "er-kennen":

                          

(wobei z.B. scheiß =  17 x + Æ und egal = );

nebenbei: bei der Anwendung des "1. Binomi" muss u.a. ( )2  berechnet werden. Dazu muss man aber gar nicht wissen, was  geschweigedenn ist, sondern das Quadrat macht einfach nur die rückgängig, und somit ergibt sich

( )2    = .)

(Man sollte in 9x 2 + 24   x •   y   + 25 y  2  die Binomi-Form

[vorne was Quadriertes, in der Mitte was Gemischtes, am Ende wieder was Quadriertes]

erkennen und sich dennoch nicht allzu sicher sein, dass tatsächlich ein Binomi vorliegt

[was im vorliegenden Fall tatsächlich nicht der Fall ist];

bei der "quadratischen Ergänzung" wird man sowas aber dennoch brauchen: wenn kein Binomi vorliegt, sorgt man eben "einfach" dafür, dass doch ein Binomi vorliegt:

  )

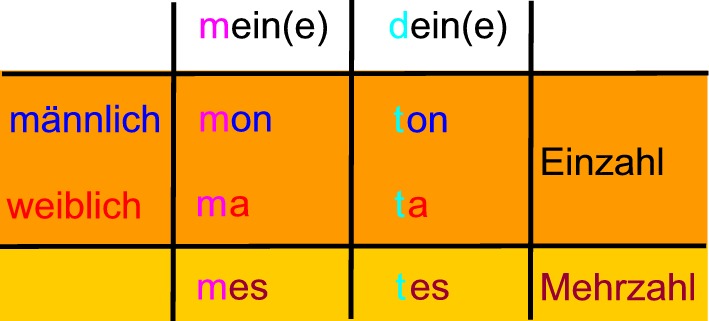
Richtig schön bunt geht's natürlich auch in allen anderen Fächern - also z.B. Französisch: