Schüler am Funktions-Fließband

Nehmen wir die erstbeste (quadratische) Funktionsgleichung  y  =  x ² + 4 x  + 5. Diese Funktionsgleichung ist erstmal eine Anweisung, wie man

• zu jedem beliebigen (unendlich vielen)  x
• immer auf dieselbe Weise
• das zu diesem  x  zugehörige  y  berechnen kann.

Die Funktionsgleichung   y  =  x ² + 4 x  + 5 schweißt also unendlich viele Zweierpärchen

,

die jeweils aus einem  x  und einem zugehörigen  y  bestehen, etwa so zusammen wie

Man könnte auch sagen: die Funktionsgleichung  y  =  x ² + 4 x  + 5 ist eine Maschine,

• in die man vorne jedes beliebige  x  eingeben kann,
• die aber mit den verschiedenen  x  dennoch immer auf dieselbe stumpfe Art und Weise rechnet,
• so dass hinten meist unterschiedliche, aber immer zum jeweiligen  x  passende  y  rauskommen.

Diese Funktions-Maschine ist also

• einerseits sehr vielseitig, da man vorne unterschiedlichste (unendlich viele)  x  eingeben kann

(ich wüsste in der "Wirklichkeit" nur eine einzige Maschine, in die man vorne [fast] alles eingeben kann und die alles gleichermaßen verarbeitet, nämlich zerstört: der Schredder:

• andererseits aber doch ziemlich einseitig: egal, welches  x  man vorne eingibt, es wird immer auf dieselbe Art und Weise zum zugehörigen  y  verarbeitet.

• schlimmste nervtötende Sklavenarbeit,
• diese aber rasend schnell und überaus verlässlich.

Im Hinblick auf Schüler bedauere ich es oft,

• dass etwa bei den Kongruenzabbildungen

(also Verschiebung, Drehung sowie Punkt- und Achsenspiegelung)

meistens

• nur der Anfangs-
• und der Endzustand ,
• nicht aber die kontinuierliche Veränderung zwischen Anfangs- und Endzustand

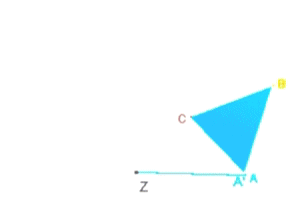
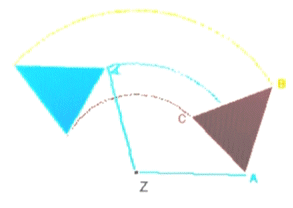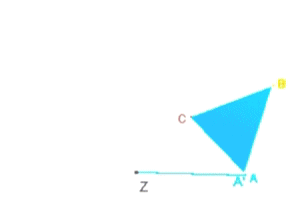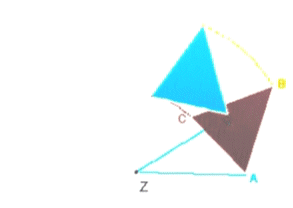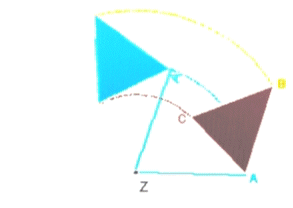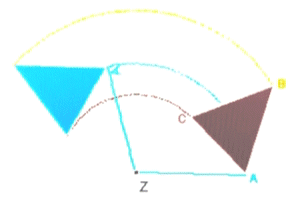
gezeigt wird,

• dass im Unterricht üblicherweise
  • ausschließlich fertige und vollständige Funktionsgraphen gezeigt werden
    

,

• nicht aber deren sukzessive Entwicklung, also eine langsam entdeckende "Bergwanderung" von links nach rechts:

Die Lage jedes Punkts  P (  x  |  y  ) ist dabei bestimmt durch seine beiden Koordinaten  x   und  y   :

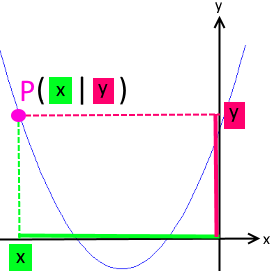
Dabei wird zu einem beliebigen  x  mittels der Funktionsgleichung

(im vorliegenden Fall   y  =  x ² + 4 x  + 5 )

das zugehörige  y   berechnet.

In

• erscheinen nacheinander elf Punkte, für die zu dem jeweiligen  x  das jeweils passende  y    berechnet werden muss,

• so dass insgesamt elf Rechnungen nötig sind.

(Dabei ist noch nichtmal berücksichtigt, dass für die dünne durchgehende blaue Linie noch sehr viel mehr, nämlich eigentlich unendlich viele unendlich nah beieinander liegende Punkte berechnet werden müss[t]en.)

Unendlich viele Punkte berechnen kann aber nichtmal ein Computer, da auch er, so schnell er auch rechnen kann, dafür unendlich lange Zeit benötigen würde. Deshalb behelfen sich Computer mit zwei Tricks:

1. berechnen sie nur Punkte, die nah genug beieinander liegen, damit das menschliche Auge die Lücken zwischen ihnen nicht mehr erkennen kann,
2. können Computer eigentlich nur eines sehr einfach zeichnen, nämlich Geraden oder genauer Strecken. Deshalb setzen sie

(was im Hinblick auf die Ableitung hochinteressant ist)

auch krumme Funktionsgraphen aus (geraden) Strecken zusammen, indem sie

• relativ wenige Punkte berechnen,
• diese Punkte mit Strecken verbinden:

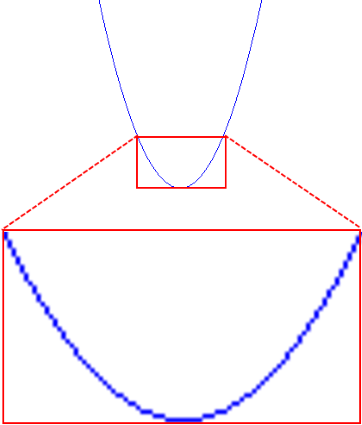
Wenn aber die Punkte nah genug beieinander liegen, erkennt das menschliche Auge gar nicht mehr, dass der scheinbar krumme Funktionsgraph in Wirklichkeit aus vielen sehr kurzen Strecken zusammengesetzt sind und daher Knicke haben.

Auf jeden Fall aber rechnen Computer derart schnell, dass in sehr kurzer Zeit ein kompletter Funktionsgraph(-ausschnitt) erscheint.

Es ist wie bei einem Film, der aus ganz vielen, sehr schnell nacheinander erscheinenden Standbildern besteht, die vom menschlichen Auge allerdings als kontinuierliche Bewegung wahrgenommen werden:

Und umgekehrt kann sich eine sehr schnelle Bewegung für das menschliche Auge zu einem Standbild verfestigen:

Ein fertiger, durchgezogener Funktionsgraph ist also sozusagen eine tiefgefrorene Version von massenhaft

(potentiell unendlich vielen)

Rechnungen auf einmal.

Man könnte also auch sagen: ein fertiger Funktionsgraph ist unendlich viele Rechnungen.

Genau das ist ja der Vorteil von Funktionen und der Grund, weshalb sie in der (Schul-)Mathematik so eine besonders wichtige Rolle spielen: dass sie - wie schon gesagt - Allesfresser sind, man nämlich mit ihnen

• für jedes beliebige, also unendlich viele  x 

• das jeweils zugehörige  y   erhalten kann (könnte).

Oder negativ gesagt: dass man sich gar nicht mehr mühsam um schnöde Einzelfälle (also z.B.    x  =  3  oder  x  =  - 217,38 ) kümmern muss.

Es reicht doch zu wissen, wie man zu jedem beliebigen   x  das zugehörige  y  erhalten kann, und es interessiert Mathematiker doch nicht die Bohne, welches  y  man erhält, wenn man z.B.  x  = wählt:

1. ist die Rechnung mit der fiesen Zahl  x  = viel zu mühsam und fehleranfällig

(Mathematiker sind stinkend faul und oftmals miserable Rechner!),

2. ist  x  = doch eine arg willkürliche Zahl,

3. hat man mit der Rechnung für  x  = arg wenig erreicht, da noch unendlich viele andere  x  übrig bleiben.

Summa summarum:

eine Funktionsgleichung wie  y  =  x ² + 4 x  + 5

• ist nicht nur eine Maschine, die rasend schnell nacheinander zu jedem beliebigen   x  das jeweils zugehörige  y  berechnet,
  
• sondern sie berechnet sogar zu allen (= unendlich vielen)   x  das jeweils zugehörige  y   gleichzeitig im selben Augenblick!

Mein Vorschlag ist es nun, die Schüler im Unterricht immer mal wieder zu solchen Maschinen zu machen (degradieren).

Das sei hier mal exemplarisch anhand der Funktionsgleichung  y  =  x ² + 4 x  + 5 vorgeführt.

Dazu sei vorweg kurz analysiert, welche Rechnungen bei  y  =  x ² + 4 x  + 5 denn eigentlich durchgeführt werden müssen:

• der Gesamt-Funktionsterm besteht aus den drei Teil-Termen ,  und

(man könnte auch sagen, die Gesamt-Maschine besteht aus den Teil-Maschinen ,  und ),

• deshalb muss das gewählte   x 

(z.B.  x  =  3  )

1. in den ersten Teil-Term eingesetzt werden

(für  x  =  3  ergibt sich dann =  9  ),

2. in den zweiten Teil-Term eingesetzt werden

(für  x  =  3  ergibt sich dann  =  12 ),

und müssen zuguterletzt

3. die Ergebnisse aus 1., 2. sowie der dritte Teil-Term =  5  aufaddiert werden

(für  x  =  3  also  9  +  12  +   5  =  26  ).

4. ist diese Summe dann das Endergebnis  y
   

(für x  =  3  also  y  =  26  ).

Ein zugehöriges Flussdiagramm könnte also so aussehen:

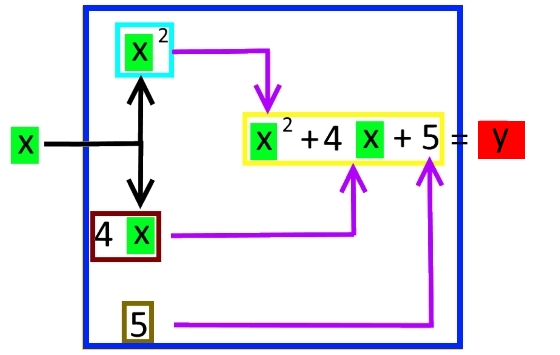
Wenn wir nun beispielsweise wie oben   x  =  3  wählen, so ergibt sich

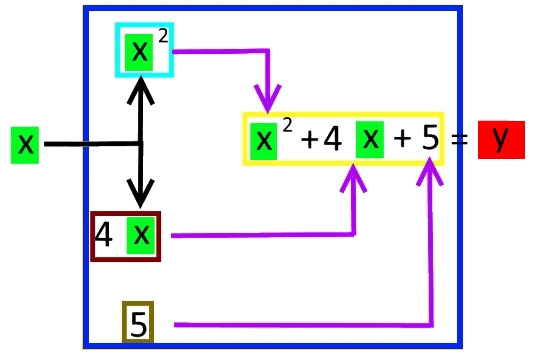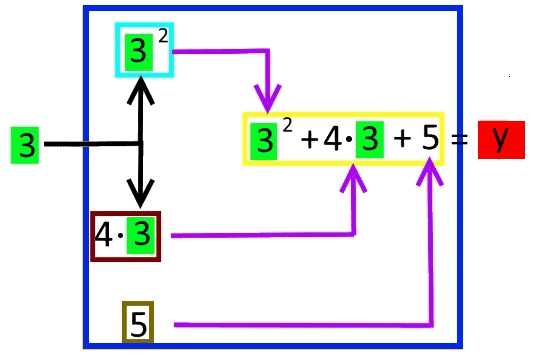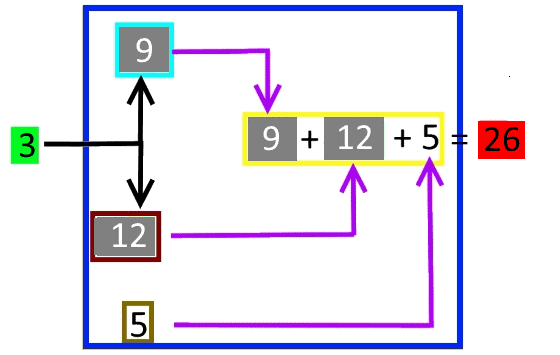
(Ich bin mir - nebenbei gesagt - noch nicht ganz sicher, ob solche Flussdiagramme

• für Schüler viel zu kompliziert sind
• oder sehr viel mehr bzw. überhaupt erst mal in Schulen durchgenommen werden sollten

[statt der einige Zeit modischen "mindmaps", die oftmals denselben Nachteil haben wie Flussdiagramme: dass man schon strukturiert denken können muss, bevor man sie erstellen kann - und dass sie dann schon fast überflüssig sind. Kein Wunder also, dass beim naiven Einsatz von mindmaps

(wie bei vielen anderen neumodischen Methoden)

meistens nur Kraut & Rüben herauskommen.

Weil ich dazu neige, alles erstmal wörtlich zu nehmen, würde mich aber eine Möglichkeit interessieren, dass beim einem Flussdiagramm wirklich etwas über verschiedene [teilweise parallele, teilweise serielle] Staustufen [= Teil-Terme/-Maschinen] fließt:

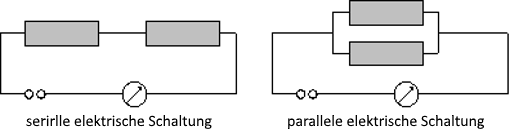
Und schon frage ich großer Modellbauer vor dem Herrn mich, ob und wie man das obige Flussdiagramm in eine Kinder-Wasserbahn oder eine illustrative elektrische Schaltung umsetzen könnte, in der nacheinander Lichter angehen.

Immerhin sei hier aber ein "Fluss", also Dynamik, mal angedeutet:

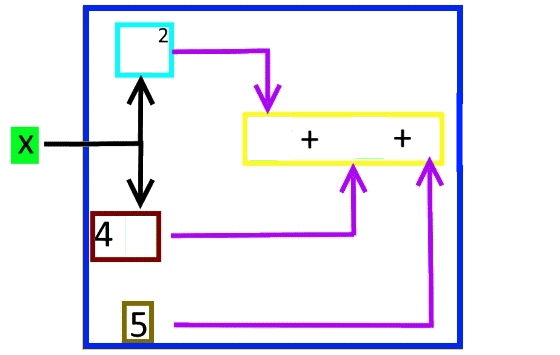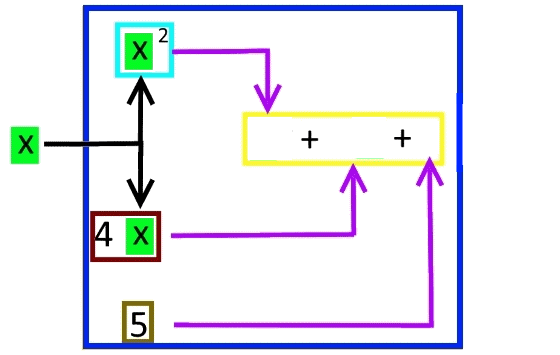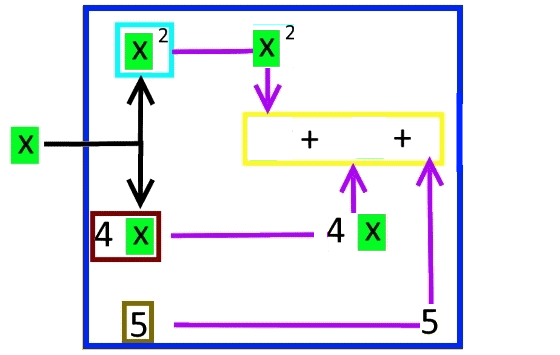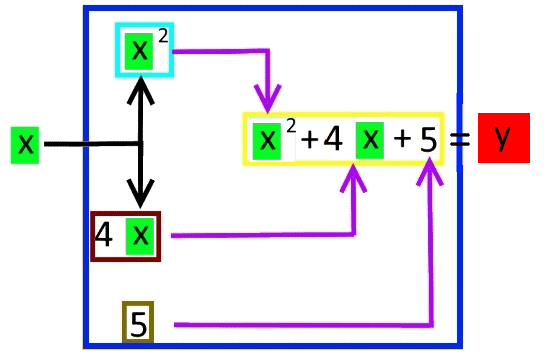
Wie auch immer:)

Schauen wir uns das Flussdiagramm aber nochmals detailliert an:

• die Gesamt-Maschine
• besteht nun aus vier Teil-Maschinen, nämlich
  • der ersten Teil-Maschine , die jedes ankommende  x  gnadenlos quadriert,
  • der zweiten Teil-Maschine , die jedes ankommende  x  stumpf vervierfacht,
  • der dritten Teil-Maschine , die wir gleich noch genauer betrachten werden,
  • der vierten Teil(?)-Maschine .
    

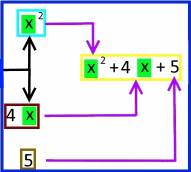
Diese vierte und im Vergleich mit oben neue Teil-Maschine

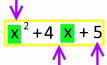
• ist sozusagen die End-Montage der in den anderen Teil-Maschinen vorgefertigten Zwischenprodukte,

• bzw. beim Autobau spricht man da auch von der "Hochzeit", womit der Augenblick gemeint ist, in dem die vorgefertigte Karosserie und die vorgefertigte Bodengruppe  zum  vollständigen Auto  zusammengefügt werden:

Interessant ist aber auch die dritte Teil-Maschine : im Flussdiagramm führte vom anfänglichen  x  kein Pfeil zu hin, da  x  ja in der Teil-Maschine gar nicht vorkommt.

Ebensogut hätte man vom anfänglichen  x  aber durchaus auch einen Pfeil zu zeichnen können, nur

• macht die Teil-Maschine nichts mit diesem  x  , ist also stinkend faul:

• sie beläßt es bei , egal, welches  x  bei ihr angeliefert wird, so dass man auch sagen könnte:

• die Teil-Maschine wirft jedes beliebige  x  , das bei ihr angeliefert wird, umgehend weg

(wir werden deshalb zur Teil-Maschine unten eine ebenso gemütliche wie lustige Schülergruppe bilden).

Nun doch mit einem Pfeil vom anfänglichen  x  zur dritten Teil-Maschine ergibt sich folgendes vereinfachtes Flussdiagramm:

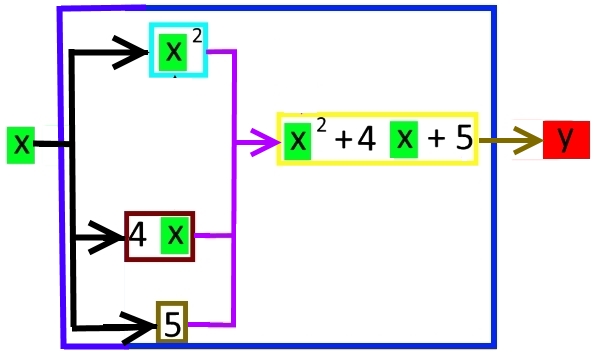
Oder elektrisch ausgedrückt:

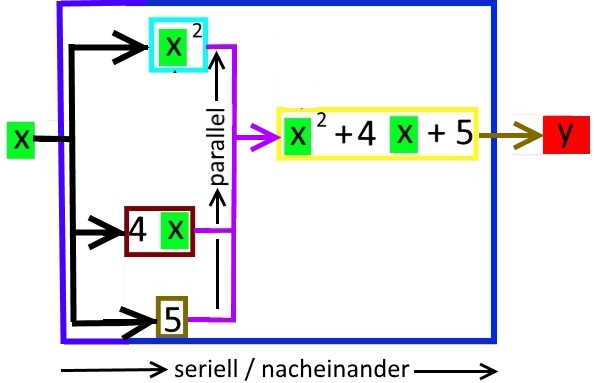
Nun verwandeln wir den Klassenraum samt den darin sitzenden Schülern in eine Funktionsmaschine. Dabei könnte der Sitzplan z.B. so aussehen:

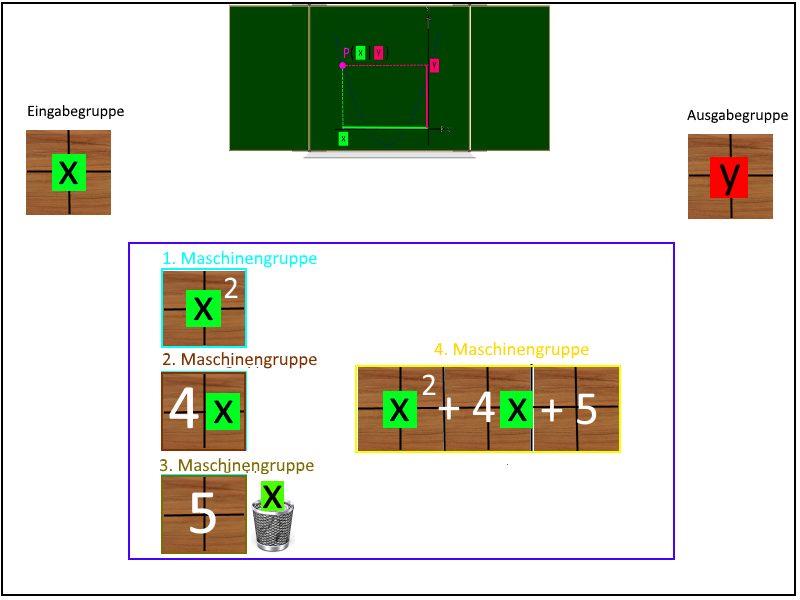
Dabei lohnt es durchaus,

• die Schülergruppen farblich zu markieren,

• um die Gesamt-"Maschine" mit blauem Klebeband auf dem Boden zu markieren,

• für die 3. Schülergruppe einen Papierkorb bereitzustellen

• d.h. alles so anschaulich und "handgreiflich" wie möglich zu machen.

Das Flussdiagramm, das man natürlich mit den Schülern vorher erarbeiten müsste, sähe dann so aus:

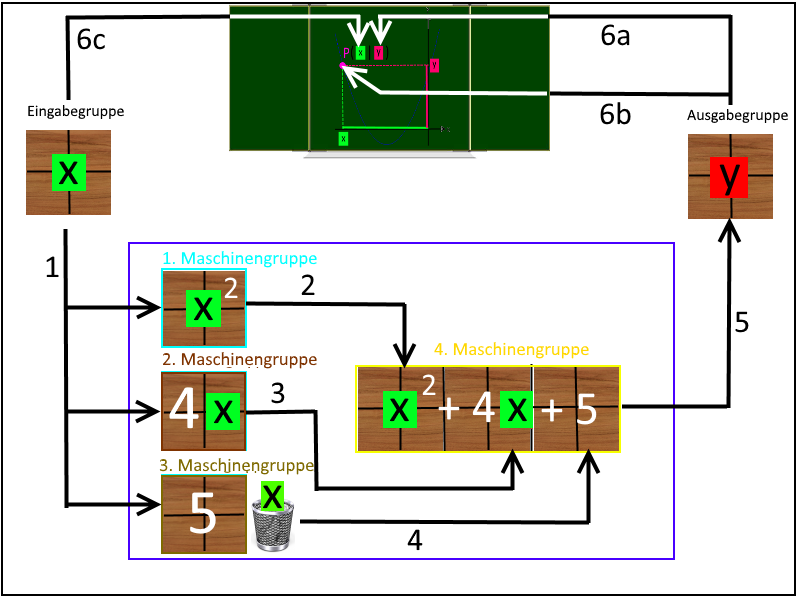
Dabei gilt folgende, wiederum mit den Schülern vorweg zu erarbeitende Vorgehensweise:

• die Kommunikation zwischen den Gruppen erfolgt ohne verbale Kommunikation zwischen den Gruppen, sondern zwischen diesen nur mittels weitergereichter Zettel, damit die 4. Maschinengruppe nicht gleich zu Anfang sofort den Gesamt-Term ausrechnen kann;

• die Eingabegruppe wählt für  x  eine beliebige Zahl und schreibt auf drei Zettel

(Beispiel-Zettel  x  =  3  ; am Anfang könnten vom Lehrer an die Gruppen vorgefertigte Blanko-Zettel verteilt werden);

• Pfeil 1: die Eingabegruppe bringt die Zettel zur. 1., 2. und 3. Maschinengruppe;

• auf die Tische der 1., 2., 4. und 4. Gruppe sind groß die jeweiligen Terme , , und geklebt;

• die 1., 2. und 3. Maschinengruppe setzen die für  x    gewählte Zahl  in ihre Terme , , ein

(die 3. Maschinengruppe wirft den ihr überreichten  x -Zettel allerdings sofort in den bereitstehenden Mülleimer);

• Pfeile 2., 3. und 4: die 1., 2. und 3. Maschinengruppe reichen ihre Ergebnisse auf Zetteln an die jeweiligen Plätze der 4. Maschinengruppe weiter

(die Zettel sehen dann z.B. für  x  =  3  so aus: = 9 / = 12 / 5 );

• die 4. Maschinengruppe berechnet daraus die Summe   und schreibt das Ergebnis auf einen Zettel; Beispielzettel:  y  =  26

• Pfeil 5.: die 4. Maschinengruppe reicht den Zettel an die Ausgabegruppe weiter;

• Pfeil 6a: die Ausgabegruppe schreibt die  y -Koordinate hinter den Punkt P an die Tafel

(also z.B. P (   |   26   ) );                                                                                                       

• Pfeil 6c: die Eingabegruppe schreibt jetzt erst die  x -Koordinate hinter den Punkt P an die Tafel

(also z.B. P (  3   |    ) );

• Pfeil 6b: die Ein- und Ausgabegruppe trägt gemeinsam den Punkt P in das Koordinatensystem an der Tafel ein

(also z.B. den Punkt P (  3   |  26  ) , wobei dieser Punkt allerdings kaum ins Koordinatensystem passt

[was Anlass sein könnte, geeignetere  x  und damit geeignetere Punkte P (  x   |  y  )  zu suchen]);

• danach scheint es mir sinnvoll zu sein, nochmals den "Gesamt-Fluss" laut mit der ganzen Klasse zu besprechen;

• als Nächstes wird ein weiterer Punkt Q (   |   ) definiert und beginnt alles mit einer anderen Zahl für  x  von vorne;

• inzwischen hat ja auch die Industrie es bemerkt: Fließbandarbeit ist insbesondere dann eintönig, wenn immer dasselbe getan werden muss - woraus man zwei Folgerungen ziehen kann:

  • die Gruppen wechseln ab und zu

(z.B.: wer eben andauernd rechnen musste, darf jetzt zur Abwechslung mal ausrechnen oder sich wohlverdient bei erholen),

• es wird alles für eine neue Funktion umgeräumt und damit neu losgelegt.

Anfangs, so glaube ich, lohnt der äußere Aufwand, auf die Dauer aber wird man wohl ohne ihn auskommen können.

Ein Problem besteht wohl darin,

• dass einerseits Routine erreicht

(bis die Ergebnisse zügig berechnet werden und verlässlich richtig sind)

und sogar die Stumpfheit der Tätigkeit "durchlitten" werden soll,

• andererseits aber genau dann die Schüler (zudem zu individuell verschiedenen Zeiten) Langeweile empfinden, deshalb unruhig werden und evtl. völlig abschalten.