
oder
die Freuden
 des Rechnens
des RechnensMehrfachbrüche

oder
die Freuden  des Rechnens
des Rechnens
Natürlich ist  hier nur
ein Eyecatcher. Wenn das jemandem zu unsachlich, anzüglich oder einfach
sexistisch ist, lese er doch mal hier nur
ein Eyecatcher. Wenn das jemandem zu unsachlich, anzüglich oder einfach
sexistisch ist, lese er doch mal    . . |
Als "reinen" Mathematiker
(bzw. „nur“ Mathematiklehrer)
interessieren mich reichlich wenig
(vgl.
![]() Anschauung statt Anwendung ),
Anschauung statt Anwendung ),
In einer einzigen Beziehung bin ich wohl wirklich ein bedeutender Mathematiker: ich verrechne mich andauernd:
meine Schüler haben immer geschmunzelt, wenn ich mich schon wieder verrechnet hatte
(dafür
stimmten meine Ergebnisse aber meistens so  , weil ich gut in
Überschlagsrechnungen bin; und
meine Rechenfehler sind mir meistens
immerhin aufgefallen, weil ich Verständnis
für die Aufgaben hatte und
damit geahnt habe, was [ungefähr] rauskommen
musste).
, weil ich gut in
Überschlagsrechnungen bin; und
meine Rechenfehler sind mir meistens
immerhin aufgefallen, weil ich Verständnis
für die Aufgaben hatte und
damit geahnt habe, was [ungefähr] rauskommen
musste).
Ich glaube aber nicht, dass meine Schüler jemals an meiner mathematischen Kompetenz
(soweit es die Schulmathematik betrifft)
gezweifelt haben, und so gesehen habe ich ihnen vielleicht doch etwas Wichtiges vermittelt, nämlich den Unterschied zwischen Mathematik und Rechnen
Nebenbei: ich hatte mal einen Schüler, der exzellent im Kopfrechnen, aber (gelinde gesagt) mäßig in Mathematik war. Wenn mal wieder eine Rechnung anstand, wurde er kurz aus seinem Tiefschlaf geweckt, lieferte er prompt das (immer korrekte) Rechenergebnis – und versank er sofort wieder im Tiefschlaf.
In der fünften Klasse nimmt man gerne mal Mehrfachbrüche
(also Brüche aus Brüchen)
wie z.B.
![]()
durch.
Solche Mehrfachbrüche kann man bis zum Exzess treiben. Vgl. etwa
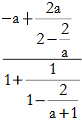
(ein
Mehrfachbruch, der sich – wie im Beispiel unten – zum simplen Bruch ![]() vereinfachen läßt),
vereinfachen läßt),
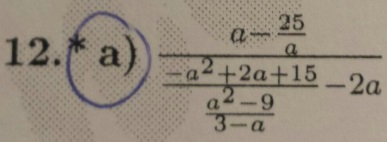
(ein fast schon perfides Beispiel, weil da auch noch binomische Formeln in einen Mehrfachbruch gequirlt wurden;
überhaupt scheint mir zumindest auf den ersten Blick, dass beide Mehrfachbrüche nur geschaffen wurden, um Schüler zu quälen, aber keinen innermathematischen Erkenntnisgewinn [s.u.] ermöglichen).
Um den Umgang mit solchen Mehrfachbrüchen zu trainieren und fast schon zum Automatismus werden zu lassen, ist es manchmal ja sogar durchaus sinnvoll, einen ganzen Stapel solcher Mehrfachbrüche abzuarbeiten und immer kompliziertere Beispiele zu wählen.
Nun muss man ja manchmal übertreiben, aber es bleibt doch zu ergänzen, dass in der Schulmathematik bis zum Abitur nie wieder solch komplizierte Umgeheuer wie beispielsweise
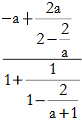
auftauchen
(mal abgesehen von irgendwelcher Anwendungs- oder gar „Lebensnähe“).
Da wäre es aber doch schön, wenn das Hantieren mit Mehrfachbrüchen immerhin einen innermathematischen Erkenntnisgewinn
(der über das im Standardunterricht übliche pure Hantieren mit Mehrfachbrüchen hinausgeht)
erbrächte.
Ein Beispiel für solch einen innermathematischen Erkenntnisgewinn ist

(Dieses
Beispiel stammt aber aus einem satirischen  Text über die Mathematik
in
Text über die Mathematik
in
 und ist da
mit dem Kommentar versehen:
und ist da
mit dem Kommentar versehen:
„Wem erschließt sich auch schon die Bedeutung [dieses] Zeichenkonstrukts?“:
eine offensichtlich rhetorische Frage mit der indirekt mitgelieferten Antwort: „sowas erschließt sich niemandem oder zumindest keinem halbwegs normalen Menschen“, was wiederum impliziert: „wenn sich sowas trotzdem jemandem erschließt [nämlich Mathematikern], ist er eben nicht ganz normal, sondern ganz schön bescheuert“.
Der Gag ist nun aber, dass der Autor des Textes offensichtlich ziemliche Ahnung von Mathematik hat, der Text also selbstironisch ist.
Nebenbei:

erinnert mich doch sehr an ein

Mobile,
und es als Mobile zu bauen
[und später unten immer weitere Ebenen anzuhängen]
wäre durchaus didaktisch hilfreich.)
Nun würde ich aber den Bruch

„der Ordnung halber“ so schreiben:

Da kann man sich zu allererst wundern, warum auf der untersten Ebene immer umständlich 3+1 statt einfach das Ergebnis dieser einfachen Rechnung, also 4, steht – und lernt damit schon Wichtiges über die Mathematik:
(Ausnahme ist da allerdings sowieso in der obersten Zeile die 2, die vermutlich gewählt wurde, weil sie genau in der Mitte zwischen 1 und 3 liegt);
Es lohnt sich also, ab und zu NICHT ZU RECHNEN!
Nun würde ich allerdings mit Schülern nicht gleich mit dem 5-Ebenen-Bruch
 ,
,
sondern mit dem 2-Ebenen-Bruch
![]()
anfangen: dieser läßt sich zu ![]() vereinfachen.
vereinfachen.
Nächster Schritt wäre dann der 3-Ebenen-Bruch
![]() ,
,
der sich zu 2 vereinfachen läßt.
(Nebenbei: hier lernen die Schüler wieder etwas durchaus Wichtiges: man vereinfacht diese Brüche immer
Viel wichtiger ist aber, was jenseits der schnöden Rechnung liegt: einige Schüler werden an diesem 3-Ebenen-Bruch vielleicht schon das Konstruktionsprinzip und damit die Fortsetzung zum 4-Ebenen-Bruch erkennen:

(... und dann wohl auch die Fortsetzung mit immer weiteren, also potentiell unendlich [!] vielen Ebenen: eine für Fünftklässler im Standard-Matheunterricht niemals vorkommende Erkenntnis, die ich aber durchaus für möglich halte
[und sich beispielsweise durch die Analogien


Sierpinski-Dreieck
und

illustrieren ließe:
ist es nicht phantastisch?: indem der menschliche Geist eine Ahnung von der Unendlichkeit bekommt
 ,
,
transzendiert er alle realen Möglichkeiten. Und Fünftklässler mögen Schwierigkeiten mit der Standard-Schulmathematik haben, aber blöd sind sie nicht.)
Wenn man nun

eben doch rechnerisch vereinfacht, ergibt
sich wieder ![]() wie schon beim
2-Ebenen-Bruch.
wie schon beim
2-Ebenen-Bruch.
Da könnte man auf die Idee zu einer weiteren Verallgemeinerung kommen:
Zwecks Überprüfung der soeben aufgestellten Vermutung könnte man die Schüler immerhin noch

bzw.


vereinfachen lassen.
Und in der Tat ergibt sich der Vermutung entsprechend
Wahrscheinlich kommen Fünftklässler nicht von selbst drauf, was der Grund für diese abwechselnden Wiederholungen ist, aber da kann man ja als Lehrer ein wenig nachhelfen:
man vergleiche mal Brüche mit demselben Ergebnis, also
![]()
![]() .
.
Da kommt beim 3-Ebenen-Bruch zusätzlich zum 1-Ebene-Bruch unten der Bruch
![]()
hinzu, der sich zu 1 vereinfachen läßt:
![]()
Somit ist der 3-Ebenen-Bruch letztlich dasselbe wie der 1-Ebene-Bruch, läßt er sich also ebenfalls zu 2 vereinfachen.
![]()
 .
.
Da kommen beim 4-Ebenen-Bruch zusätzlich zum 2-Ebenen-Bruch unten zweimal die Brüche
![]()
hinzu, die sich aber wieder beide zu 1 vereinfachen lassen:

Somit ist der
4-Ebenen-Bruch letztlich
dasselbe wie der
2-Ebenen-Bruch, läßt er sich also ebenfalls
zu ![]() vereinfachen.
vereinfachen.
(Und schon haben die Schüler wieder eine wichtige mathematische Tätigkeit gelernt:
[und zwei täuschend ähnliche Dinge in Wirklichkeit oft sehr unterschiedlich];
[auch für gestandene Mathematiker]
sehr
Kompliziertes sich oftmals
glücklicherweise enorm vereinfachen
läßt:
z.B. ist der 1000-Ebenen-Bruch letztlich dasselbe wie der
2-Ebenen-Bruch, also ![]() .)
.)
Was Fünft(!)klässler hier so nebenbei implizit lernen, ist nichts Geringeres als das eminent wichtige und staunenswert genial-einfache mathematische Beweisverfahren der (hochtrabend gesagt) „vollständigen Induktion“
(hier allerdings für jeden zweiten Bruch),
das leider nichtmal viele Oberstufenschüler kennenlernen:
(Die „vollständige Induktion“ läßt sich Fünftklässlern auch so illustrieren:
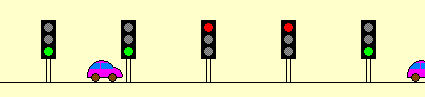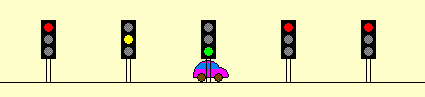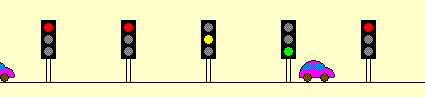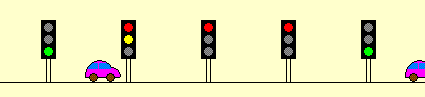
"Welle" wohl deshalb, weil
die Ampeln natürlich nicht alle gleichzeitig grün sind,
sondern wellenförmig nacheinander
[immer gerade dann, wenn man nacheinander bei ihnen ankommt].
Zu einer einzigen Zeit sehen sie also etwa so aus:
 )
)
Wenn man den Mehrfachbruch

immer weiter nach unten fortsetzt, ergibt
sich also abwechselnd
immer wieder abwechselnd ![]() und 2.
und 2.
Nun gibt es aber unendlich lange sogenannte „Kettenbrüche“ der Form
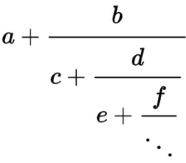 ,
,

also z.B.
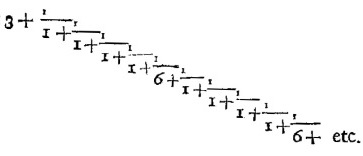
(in Leonard Eulers "De usu novi algorithmi in problemate
Pelliano solvendon" von 1767)
die
(mehr oder minder schnell gegen diesen einen Wert „konvergieren“).
Besonders interessante Beispiele sind da
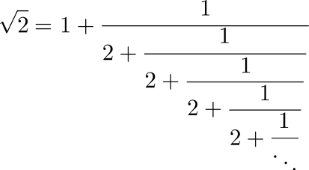 ,
,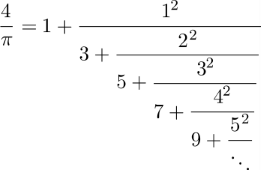 .
.In beiden Fällen passiert etwas Erstaunliches:
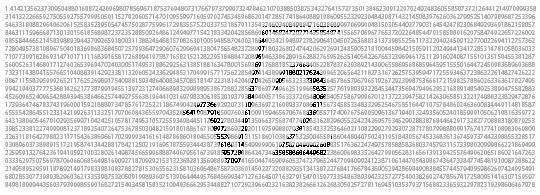 ,
, (gesprochen
"pi") auf:
(gesprochen
"pi") auf:sowohl
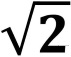 als auch
als auch  sind aber
sogenannte „irrationale“ Zahlen, d.h.
sind aber
sogenannte „irrationale“ Zahlen, d.h.
(weshalb
mir - wenn
schon, denn schon - die Dezimaldarstellungen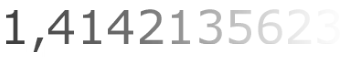 und
und
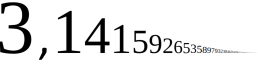 am liebsten sind).
am liebsten sind).
Aber immerhin kann man sowohl
![]() als auch
als auch ![]() durch einen immer länger werdenden
Mehrfachbruch beliebig nah annähern.
durch einen immer länger werdenden
Mehrfachbruch beliebig nah annähern.
(Da man aber nicht unendlich lange rechnen kann [und will], wird man sie nie exakt erreichen: und es gibt auch keine andere Möglichkeit, sie exakt zu erreichen!)
Allemal bemerkenswert ist auch, dass
man
![]() und
und ![]() durch
durch
(aber da scheiden sich wohl die Geister)
damit schöne (!) Mehrfachbrüche
annähern kann.
(Nebenbei: es läßt
sich sehr wohl auch schon Fünftklässlern vermitteln, wie eine auf Anhieb
scheinbar unmögliche irrationale Zahl aussehen könnte. Z.B. so: 1,0 100 1000
10000 ... Allerdings sind
![]() und
und ![]() nach dem Komma
nicht so trotz allem regelmäßig, sondern völlig
chaotisch. Um so bemerkenswerter
ist es, dass sie überhaupt durch so relativ einfache Mehrfachbrüche
annäherbar sind.)
nach dem Komma
nicht so trotz allem regelmäßig, sondern völlig
chaotisch. Um so bemerkenswerter
ist es, dass sie überhaupt durch so relativ einfache Mehrfachbrüche
annäherbar sind.)
Im Hinblick auf eine 5. Klasse ist es
unerheblich, dass die Zahlen
![]() und
und ![]() den Schüler noch nichts „sagen“.
den Schüler noch nichts „sagen“.
(Vielleicht
kennen die Schüler aber schon die Redewendung
 , die für ein
laxes „so ungefähr“ steht..
, die für ein
laxes „so ungefähr“ steht..
Dabei ist „so ungefähr“ eine schöne Umschreibung für den nie völlig genauen Annäherungsprozess, um den es bei Kettenbrüche geht.
Nebenbei:
 läßt sich
auch abkürzen zu
läßt sich
auch abkürzen zu
![]() • d und ist
somit eine
schöne Eselsbrücke für den Kreisumfang.)
• d und ist
somit eine
schöne Eselsbrücke für den Kreisumfang.)
Aber warum nicht ab und zu in die Zukunft der Schulmathematik schauen
(was im Standardunterricht, in dem man nur in der Gegenwart oder Vergangenheit lebt, fast nie geschieht)?:

Der Lehrer kann ja immerhin schonmal erwähnen, dass ![]() und
und ![]() in der späteren Schulzeit nochmal wichtig werden
in der späteren Schulzeit nochmal wichtig werden
(und in welchen Zusammenhängen das passiert).
Die Schüler können aber allemal zunehmend längere Mehrfachbrüche jeweils vereinfachen und dabei den Annäherungsprozess beobachten:
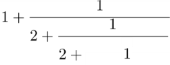 =
= 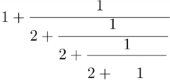 =
= 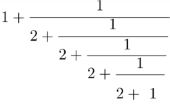 =
= (Dabei könnte auch schon
für Fünftklässler von Interesse sein, wie sich die Brüche
![]() ,
,
![]() ,
,
![]() und
und
![]() auseinander ergeben, nämlich
auseinander ergeben, nämlich
was auch eine Art "vollständige Induktion" ist
und eine Menge BruchRECHNUNG erspart)
Was die Fünftklässler bei dieser Annäherung aber lernen, ist nichts Geringeres als der
(nur noch nicht so benannte)
„Limes“!
(Nebenbei:
es gibt eine
 Internetseite, auf der
man sich
Internetseite, auf der
man sich
[die einem also die stumpfe Rechenarbeit abnimmt],
[wobei mich ja doch mal der Algorithmus interessieren würde, mit dem diese Umwandlung vorgenommen wird]:


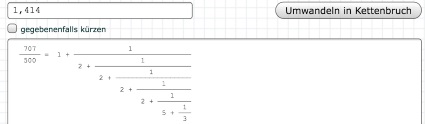
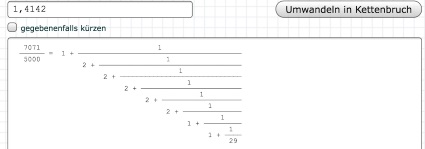 )
)
All das habe ich aber nur ausgeführt, um zu zeigen, dass hinter der auf den ersten Blick bloß stumpfen Berechnung (Vereinfachung) von Mehrfachbrüchen à la

durchaus interessante
(und schon für Fünftklässler erreichbare)
mathematische Erkenntnisse lauern.
Mein eigentliches Thema hier ist es aber, dass die in Augen eines Mathelehrers
(oder zumindest meinen Augen)
idiotische Vereinfachung langer Mehrfachbrüche in den Augen vieler Fünftklässler durchaus spannend ist, dass viele von ihnen also sehr wohl gerne RECHNEN.
Ein Beispiel: als ich mit Fünftklässlern mal Mehrfachbrüche durchgenommen habe, hat sich einer der Schüler
(ohne Anregung durch mich)
ein ganzes Wochenende hingesetzt und einen gigantischen Mehrfachbruch
(z.B. aus 50 Ebenen)
vereinfacht. Er hat dann alle Vereinfachungs-Zwischenschritte nebeneinander geklebt und ist mit der sich so ergebenden Papierschlange montags morgens stolz wie Oskar im Matheunterricht aufgetaucht. Wir haben
(ganz wichtig!)
die Papierschlange dann an die Wände des Klassenraums geklebt, wobei sich gezeigt hat, dass sie tatsächlich einmal ganz um den Klassenraum reichte:
was für ein Erfolgserlebnis nicht nur für den einen Schüler, sondern auch für seine Klassenkameraden!
(Wo im üblichen Matheunterricht hat ein Schüler jemals solch ein mit Händen fassbares Erfolgserlebnis?!)
Ich habe soeben gesagt, in den Augen eines Mathelehrers
(oder genauer: in meinen Augen)
sei die ellenlange Vereinfachung eines gigantischen Mehrfachbruchs nurmehr „idiotisch“, womit dann auch Fünftklässler, die sowas gerne machen, (noch) nur kleine Idioten sind, die schnellstmöglich zur einzig wahren Lehre, nämlich der „eigentlichen“ Mathematik; bekehrt bzw. umerzogen werden müssen:

(Quelle:
 ;
;
besonders
schnuckelig finde ich dabei das mathematische [!] Koordinatensystem mit
dem Bekehrungs-Graphen!)
So verächtlich habe ich über Schüler ja nie gedacht
(und wenn, dann nur kurz über jene Schüler-Spezies, die reflexartig „können wir nicht endlich zu Aufgaben [also zum Rechnen] zurückkehren?“ krähte, sobald ich mal interessanteren bzw. anspruchsvollen Unterricht machen wollte).
Bzw. gerade das Erlebnis mit dem soeben genannten Schüler, der einen Megabruch vereinfacht hatte, hat mich
(vor über 20 Jahren)
stutzig und dann aufmerksam gemacht:
es gibt viele, vor allem jüngere Schüler, die durchaus gerne RECHNEN.
Warum?:
(und die
Lehre von der Verschlüsselung [„Kryptographie“], also den
Geheimsprachen und –schriften, ist ja in der Tat ein Teilgebiet der
Mathematik – und wäre allemal ein lohnendes Thema für den
Matheunterricht: 
 ).
).
(was natürlich schnarchlangweilig ist, aber es gibt ja Leute, die völlig unempfindlich gegen Langeweile sind, weil diese ihrem Naturell entgegenkommt),
(Es ist wie im Fach Deutsch: wenn Schüler in einer Klassenarbeit ein Gedicht „analysieren“ sollen, fangen sie immer mit dem Strophenbau, Reimschema und Versmaß an
[sie tun das dem Lehrer zuliebe, aber nicht etwa, weil sie selbst sowas für bedeutsam halten].
Meist bleibt es bei der puren Feststellung solcher „Stilelemente“
[z.B. „das ist eine Metapher [wenn man gerade Metaphern durchgenommen hat, ist alles Metapher] und sie verbildlicht ganz ungemein“],
aber es wird kaum je gefragt, was die konkreten Stilelemente im Text leisten.
Solch eine reine Feststellung von Fakten hat immerhin den Vorteil,
[in Wirklichkeit halten die meisten Schüler nämlich sämtliche Gedichte für absolut weltfremd und „totale Scheiße“ – was sie natürlich nicht laut sagen dürfen, weshalb sie, wenn man sie nach ihrer Meinung fragt, oft schreiben: „ich finde das Gedicht »ganz gut«“].)
Viele (auch Mathelehrer) werden es kaum glauben, aber man kann auch (sogar!) in der Mathematik selbstständig denken!
(und zwar auch bzw. gerade Nichtmathematiker)
ein Mittel gegen Langeweile
![]()
und eine Art der Meditation und Erholung ist

(Für mich ist sowas hingegen derart schwachsinnig, dass ich höchstens
Aber das
ist wohl eher mein Problem: ich bin einfach auf dem Spiele- und
Knobelauge blind:
 würde mich zu Tode
langweilen.
würde mich zu Tode
langweilen.
Nebenbei: an Sudokus wird vielleicht exemplarisch der Unterschied zwischen Laien und Mathematikern klar:
den Laien interessiert wohl nur, ob ein Sudoku schwierig oder einfach ist,
den Mathematiker würde die Konstruktionsweise von Sudokus interessieren, wann sie also schwierig oder einfach sind.)
Dieser Automatismus des Rechnens ist ja durchaus faszinierend: manchmal hat man sogar das Gefühl, dass die Mathematik ein selbstständiges Wesen

ist, das auch ohne uns
(und inzwischen ja auch in Computern)
funktioniert.
Besonders faszinierend ist es aber, dass die Mathematik
(bzw. ihre Rechenregeln)
manchmal schlauer zu sein scheint als man selbst: sie führt nach langer Rechnungen oftmals zu sehr einfachen Ergebnissen, über die man nur staunen kann, weil man selbst überhaupt nicht mehr einen Überblick darüber hat, wie dieses einfache Ergebnis sukzessive zustande gekommen ist.
(Es lohnt sich aber allemal, in einem Rückblick nochmal anzuschauen, wie sich beispielsweise eine Zahl [das Endergebnis] durch all die Rechnungen geschlängelt hat.)
Lange Rechnungen, die am Ende in einem lauten

zu einem sehr einfachen und aussagekräftigen Ergebnis führen, sind wie ein Zauberer, der urplötzlich ein Kaninchen aus seinem Zylinder zieht:
Überhaupt scheint wir, das eine Menge genialer mathematischer Erkenntnisse nicht durch einen spontanen Geistesblitz zustande gekommen sind, sondern weil da jemand ewig rumgerechnet /-probiert hat und nach dem hundertsten Versuch urplötzlich etwas Erstaunliches herauskam
(und erst
als das Genie herausfand, weshalb sowas Einfaches herauskam, hatte es
sein  ).
).
