für Livia

Siehe auch am Ende das Fast-Food-Kapitel "Lösen nach Schema F".

Funktionen lassen sich auf zwei Arten darstellen:

1. algebraisch durch eine Funktionsgleichung, also z.B.

(dabei steht auf der rechten Seite der Funktionsterm [hier x² ], der zeigt, wie zu jedem x das passende y berechnet werden kann, und zwar immer auf dieselbe Weise [hier durch Quadrieren]),

2. geometrisch durch einen Funktionsgraphen, also z.B. .

Beide Arten der Funktionendarstellung haben ihre jeweiligen Vorteile:

1. : mit den algebraischen Funktionsgleichungen kann man rechnen, also exakte Ergebnisse herausbekommen und somit auch Beweise führen,

2. : die geometrischen Funktionsgraphen sind anschaulich.

Und mal braucht man dies, mal jenes - und am besten beides:

Ein zentrales Anliegen der Analysis in der Oberstufe besteht darin, beide Arten der Funktionsdarstellung zu verbinden und hin und her springen, also

• zu jeder Funktionsgleichung den Funktionsgraphen

• und zu jedem Funktionsgraphen die Funktionsgleichung

erstellen zu können:

Ziel ist also

.

Kurz erwähnt sei hier noch, dass z.B. die Funktionsgleichung nur eine Kurzversion von "y ist gleich dem Quadrat von x", also eine sprachliche Form der Funktionsdarstellung und damit

 ein Hin- und Herübersetzen zwischen Sprache und Bild ist. Vgl.

"Vorfahrt gewähren!"

Meistens sind im Mathematikunterricht Funktionsgleichungen gegeben, zu denen "Kurvendiskussionen" angefertigt werden sollen.

"Kurvendiskussionen" bedeutet dabei in der Regel, dass markante Punkte herausgefunden werden sollen, und das geschieht oftmals,

• um den zugehörigen Funktionsgraphen mit wenigen Berechnungen und Strichen zeichnen zu können

• und somit überhaupt erst eine anschauliche Vorstellung von den Funktionen zu erhalten.

Als markante Punkte werden üblicherweise angesehen

• der Schnittpunkt mit der y-Achse                        (genau einer),
• Nullstellen, also Schnittpunkte mit der x-Achse (mehrere möglich),
• der Schnittpunkt mit der y-Achse                        (genau einer),
• Minima und Maxima                                              (mehrere möglich),
• Wendepunkte                                                       (mehrere möglich),
• Sattelpunkte                                                          (mehrere möglich),

die allesamt (außer dem Schnittpunkt mit der y-Achse) nicht vorliegen müssen, sondern vorliegen können.

(Wichtig sind diese Punkte insbesondere bei Anwendungen. Wenn beispielsweise mein Kontostand eine Nullstelle hat, heißt das, dass ich pleite bin.)

Die markanten Punkte haben allesamt den Vorteil, dass bei ihnen die Rechnungen sehr einfach sind, da immer irgendwas (manchmal größer oder kleiner als)  null ist, und mit der Null lässt es sich

(wie wir unten noch dankbar erfahren werden)

besonders einfach rechnen

(nur kann/darf man nicht durch Null dividieren !):

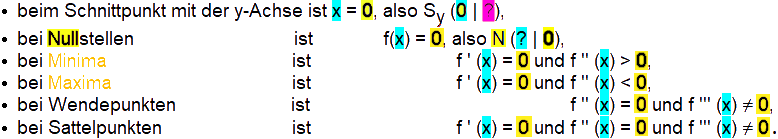
(Man muss sich also nur schlappe fünf , zudem teilweise sehr ähnliche Regeln ins Gehirn rammen

[zusätzlich braucht man eigentlich nur die pq-Formel 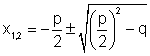für normierte quadratische Funktionen],

und dann ist alles ziemlich einfach, und zwar insbesondere, wenn es um ganzrationale Funktionen geht, die auch noch ganz einfach abzuleiten sind.

Nebenbei: man könnte die o.g. Bedingungen auch exakter und damit auch manchmal überhaupt erst korrekt formulieren, aber ich befürchte, dass im Standard-Mathematikunterricht oftmals vor lauter Exaktheit das grundlegende Verständnis flöten geht. Also Mut zur Halbwahrheit - auch in der Mathematik! Überhaupt sollte sich Schulunterricht mehr als Wissenschaftspropädeutik bzw. Populärwissenschaft denn als absolut exakte Wissenschaft verstehen. Wir brauchen also als Lehrer keine Fachwissenschaftler, die die reine Lehre verbreiten, sondern Fachdidaktiker

[nicht zu verwechseln mit den theoretischen Fachdidaktikern an Universitäten, die meist Welten von der schulischen Praxis entfernt sind und deshalb immer superschlau reden können].

Kurz ergänzt sei eine Fehlermöglichkeit bei Nullstellen und dem Schnittpunkt S_y mit der y-Achse, weil da alles "andersrum" ist:

• bei Nullstellen, also Schnittpunkten mit der x-Achse, ist y = 0,
• beim Schnittpunkt S_y mit der y-Achse ist hingegen        x = 0,

also ist alles "andersrum", als man erwarten könnte.

Das Problem ist nun aber, dass die markanten Ereignisse den Funktionsgleichungen in der Regel nicht anzusehen sind, wohl aber den Funktionsgraphen

(an denen man die markanten Eigenschaften allerdings nur ungefähr ablesen kann; wenn man's aber genau wissen will [oder muss], muss man dann eben doch mit den Funktionsgleichungen rechnen).

Nehmen wir als Beispiel für eine Funktionsgleichung mal y = x³ + 2x² .

(Unten wird noch klar werden, warum wir diese Funktionsgleichung mit dem blöden Bruch nehmen.

 Wegen der Taschenrechner haben's Schüler heutzutage ja nicht mehr so mit Brüchen - und halten sie fälschlich Dezimalzahlen für einfacher.)

Direkt im Folgenden werden wir aber sehen, dass die Funktionsgleichung y = x³ + 2x² sogar besonders einfach ist, da hinten nicht noch ein Rattenschwanz wie z.B. in y = x³ + 2x² - 7x + 3 folgt.

Einige markante Eigenschaften können wir aber durchaus schon an der Funktionsgleichung y = x³ + 2x² , also ohne jede Rechnung ablesen:

1. hat der Graph wegen des höchsten Exponenten 3 eine -Form, sieht er also etwa so aus:

Die -Form der Funktionsgraphen von Funktionen dritten Grades setzen wir bei unseren weiteren Veranschaulichungen immer als bewiesen voraus

(obwohl der Beweis im Unterricht nie vorkommt).

2. können wir vor dem Term mit dem höchsten Exponenten 3 ein Plus ergänzen, also y = + x³ + 2x² , womit nur noch Graphen übrigbleiben, die vom Negativen (links unten) ins Positive (rechts oben) gehen:

3. können wir wegen des Bruchs vor x³ sagen, dass der Graph abgeflacht ist, also so wie der schwarze Graph im Vergleich mit dem blauen.

Des weiteren können wir schon feststellen:

4. hat jede ganzrationale Funktion, also auch y = x³ + 2x² , genau einen Schnittpunkt S_y mit der y-Achse,
5. hat jede Funktion dritten Grades, also auch y = x³ + 2x² ,

• mindestens eine, aber höchstens drei Nullstellen

(also ein , zwei  oder drei  Nullstellen),

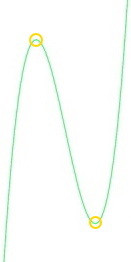
• einen Sattelpunkt oder aber ein Maximum und dann auch ein Minimum

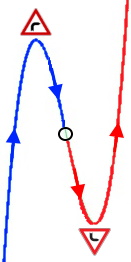
(im vorliegenden Fall y = + x³ + 2x² liegt das Maximum [falls vorhanden] links, das Minimum rechts),

• garantiert einen (einzigen) Wendepunkt, zu dem der Funktionsgraph punktsymmetrisch ist

(im vorliegenden Fall y = + x³ + 2x² hat der Funktionsgraph

• links vom Wendepunkt eine Rechtskurve

• und rechts vom Wendepunkt eine Linkskurve: ).

Einiges wissen wir aber noch nicht:

aussieht

(also wie der grüne Funktionsgraph zwischenzeitlich auch mal fällt und sowohl ein Maximum als auch ein Minimum hat - oder wie der schwarze Graph einen Sattelpunkt),

• wo genau die einzelnen markanten Punkte liegen,
• wie viele Nullstellen der Graph hat

(nur eine oder doch zwei oder sogar drei).

Um all das herauszufinden, was wir noch nicht wissen, bleibt uns nichts anderes, als loszurechnen:

1. Nullstellenberechnung, also Berechnung von N (? | 0) :

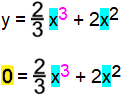
Nun ist es normalerweise mit der Schulmathematik gar nicht so einfach bis sogar unmöglich, die Nullstellen von Funktionen dritten Grades herauszufinden.

(Eine Ausnahme ist es, wenn man schon eine Nullstelle kennt

[sei's durch Ausprobieren, sei's, weil der Lehrer sie verraten hat]:

dann kann man mit der sogenannten Polynomendivision die Gleichung auf eine quadratische Gleichung reduzieren und diese [wenn's überhaupt weitere Lösungen gibt] mit der pq-Formel lösen.)

Im vorliegenden Fall ist alles aber

(wie bereits oben versprochen)

viel einfacher, da in y = x³ + 2x der Rattenschwanz wie z.B. in y = x³ + 2x² - 7x + 3 fehlt. Weil in y = x³ + 2x  aus den beiden Summanden x³ und 2x² jeweils x² ausgeklammert werden kann, erhalten wir

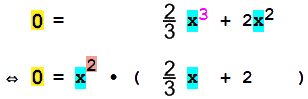
Ein erfahrener Mathematiker könnte daraus schon weitere Informationen ziehen, ohne jedoch schon weiterzurechnen: weil x² ausgeklammert werden kann, liegt im Ursprung (= Schnittpunkt der beiden Achsen des Koordinatensystems) eine doppelte Nullstelle vor, was in einem Abwasch bedeutet, dass

• der Graph dort die x-Achse berührt (und nicht schneidet),
• deshalb im Ursprung das Minimum oder das Maximum des Graphen liegt

(... und deshalb woanders noch umgekehrt das Maximum oder das Minimum  ... und genau in der Mitte zwischen beiden der Wendepunkt )

• wir schon die Nullstelle N₁ (0 | 0) haben

(... und woanders noch eine zweite Nullstelle N₂  (? | 0), aber keine dritte vorhanden ist)

• und auch schon den Schnittpunkt mit der y-Achse, also S_y (0 | 0), da der Ursprung ja auch auf der y-Achse liegt.

Damit bleiben nur noch die beiden folgenden Möglichkeiten:

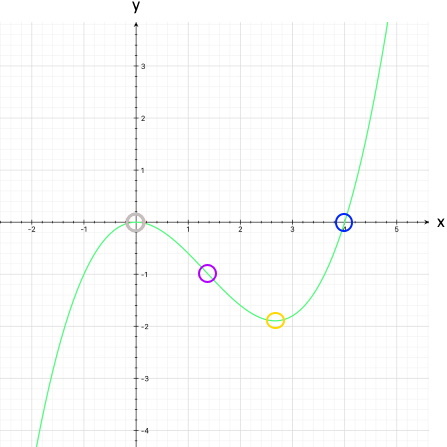
(... wobei hier nur die grundsätzliche Form stimmt, vermutlich aber nicht die konkreten Zahlenwerte für die Punktkoordinaten;
die muss man dann doch noch ausrechnen.)

Es ist doch immer schön, schon vorweg zu wissen, was (so ungefähr) rauskommen wird: dann kann man die einleitenden Gedanken und die späteren Rechnungsergebnisse miteinander abgleichen und ist nicht allzu überrascht über eventuelle merkwürdige, aber richtige Rechenergebnisse - oder erkennt Rechenfehler.

Aber rechnen wir mit 0 = x² • (  x + 2 ) doch einfach mal weiter, und zwar mit einem genialen Trick: das Produkt aus x² und (  x  + 2 )  kann nur dann 0 sein, wenn

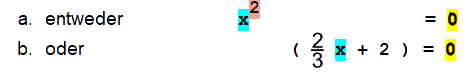
ist.

Zu a.:

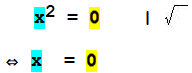
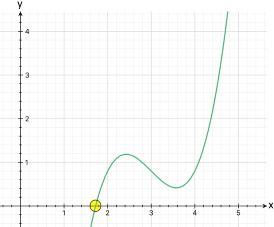
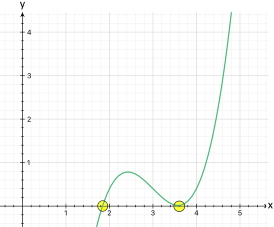
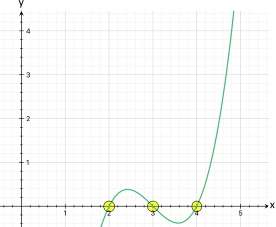
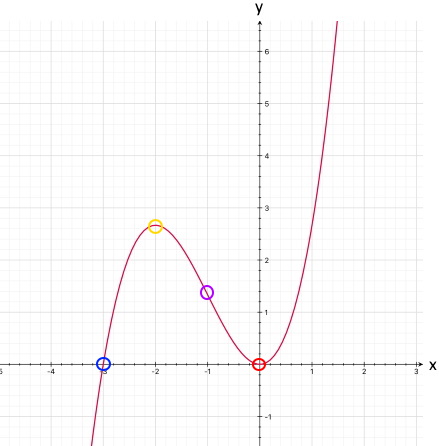
Damit haben wir schon die erste Nullstelle N₁ (0 | 0), nämlich den Ursprung, der gleichzeitig auch der Schnittpunkt mit der y-Achse ist, also S_y (0 | 0).

Zu b.:

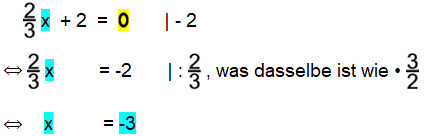
Damit haben wir die einzige weitere Nullstelle N₂ (-3 | 0).

Wenn aber nur zwei Nullstellen vorliegen, kommen wir wieder zum Ergebnis, dass der Funktionsgraph ungefähr so aussehen muss:

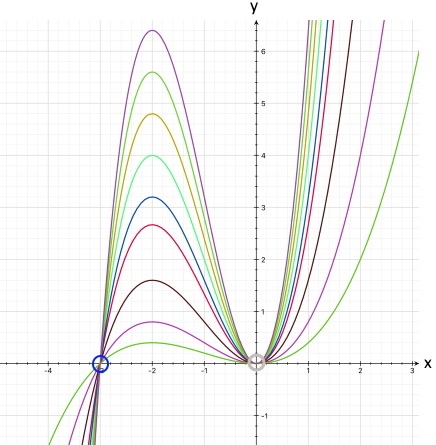 oder

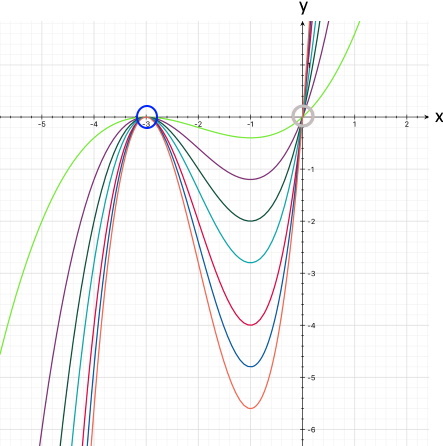
(... wobei jetzt auch die beiden Nullstellen N₁ (0 | 0) und N₂ (-3 | 0) berücksichtigt sind,
von denen einer ein Berührpunkt sein muss.)

Der Funktionsgraph

• berührt die x-Achse also entweder in N₁ (0 | 0) oder in N₂ (-3 | 0)
• und schneidet sie in der jeweils anderen Nullstelle.
  

Unklar ist aber noch, welche der beiden Möglichkeiten hier vorliegt und wie hoch bzw. tief der Funktionsgraph ansonsten liegt. Um das herauszufinden, müssen wir die Koordinaten des Maximums  bzw. Minimums berechnen.

Normalerweise haben wir zu diesem Zeitpunkt ja noch nicht so schöne (computergemachte) Grafiken, aber wo wir sie hier schonmal haben, können wir immerhin schon die Vermutung aufstellen, dass das nicht im Ursprung liegende Maximum bzw. Minimum die x-Koordinate -2 bzw. -1 hat:

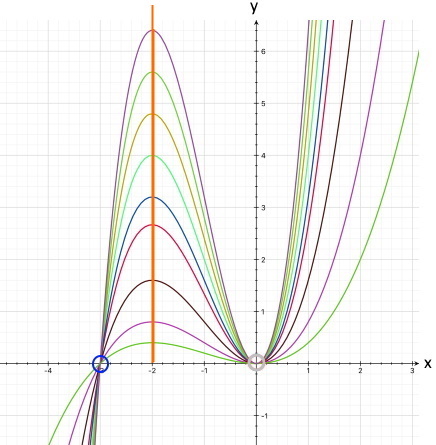
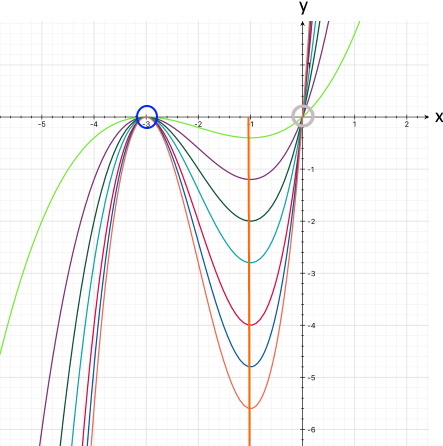
(„Vermutung", weil man von Funktionsgraphen niemals exakte Werte ablesen kann.)

2. Extremwertberechnung:

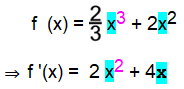
Notwendige Bedingung für einen Extremwert ist, dass f '(x) = 0, womit folgt:

      0    =  2x² + 4x

Normalerweise braucht man für die Lösung solch einer quadratischen Gleichung die pq-Formel

(nachdem man die Gleichung vorher „normiert", also die 2 vor dem x² beseitigt hat!),

aber hier geht‘s mit dem bereits oben benutzten Trick einfacher:

für und gegen   gefallen ist.

Und wir können feststellen:

• unsere Vermutung, dass der x-Wert des Maximums -2 ist, ist bestätigt worden;
• der Ursprung und nicht N₂ (-3 | 0) ist der Berührpunkt.

Aber wir wissen noch immer nicht, wie hoch der Funktionsgraph liegt. Um das herauszufinden, berechnen wir noch den zu x = - 2 gehörenden y-Wert, indem wir für x in der Anfangs-Funktionsgleichung y =  x³ + 2x²  nun - 2 einsetzen:

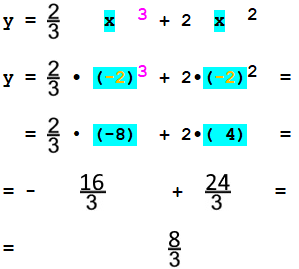
(Tja, die Bruchrechnung müsste man beherrschen. Für Bruchrechnungsanalphabeten sei aber noch ergänzt: = 2,66666666666666666666666...)

Daraus folgt für das erste Extremum M₁ (-2 | ), und damit ist dies der gesuchte Funktionsgraph:

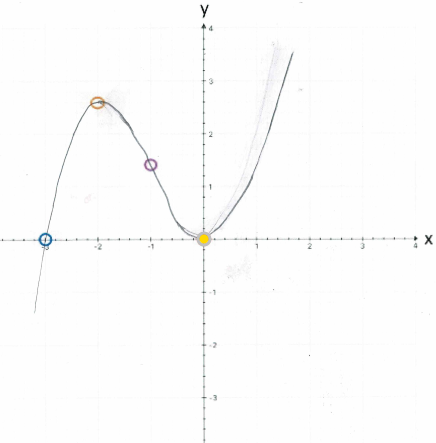
Das andere Extremum ist der Ursprung, also M₂ ( 0 | 0 ).

Und aus unseren Überlegungen geht auch schon hervor, dass M₁ (-2 | ) das lokale Maximum und M₂ ( 0 | 0 ) das lokale Minimum ist.

Wir sparen uns hier also mal die Überprüfung mittels der zweiten Ableitung, ob da ein Maximum bzw. Minimum vorliegt.

(Wieder für Bruchrechnungsanalphabeten: = 1,33333333333333333333333333333333333333333333333333333333333333...)

Aber angenommen mal, wir haben ohne jede Veranschaulichung nur völlig abstrakt bzw. sinn- und verstandlos gerechnet. Dann haben wir folgende Ergebnisse:

Diese Punkte tragen wir nun ins Koordinatensystem ein:

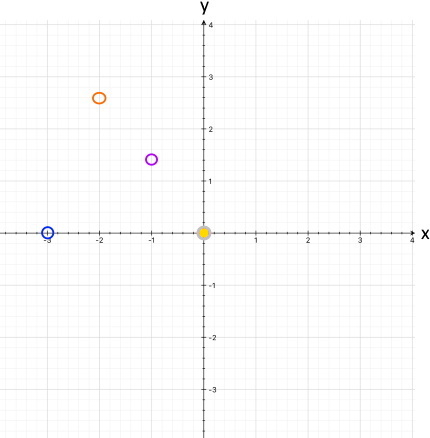
Um durch diese Punkte den kompletten Funktionsgraphen durchfriemeln zu können, müssen wir nun doch voraussetzen, dass der Funktionsgraph der Funktion f: y =  x ³ + 2  x  ² eine -Form hat.

Und damit erhalten wir dann auch

Schöner geht's mit der Hand kaum, denn unsere "Kurvendiskussion" läuft ja darauf hinaus,

• nicht alle Punkte des Graphen zu berechnen und dann einzuzeichnen

(was auch gar nicht ginge, da es unendlich viele Punkte sind),

• sondern nur die "markanten" Punkte.

Zwischen diesen wenigen Punkten müssen wir dann aber mit der Hand die Verbindungslinien einzeichnen.

Ein Computer kann's natürlich schöner, weil er zwar auch nicht alle, also unendlich viele Punkte berechnet, aber doch in rasender Geschwindigkeit sehr viele:

 Es hat also Vor- und Nachteile, einen Computer zu benutzen:

• mit ihm bekommt man natürlich einen fast perfekten Graphen,
• lernt man aber nichts über die markanten Punkte.

Insgesamt haben wir aber ENDLICH unser Ziel bzw.

y =  x ³ + 2  x  ²  

erreicht und verbinden wir mit y =  x ³ + 2  x  ² ENDLICH die Vorstellung !

Amen.

Aber eine kleine Anmerkung kann ich mir hier doch nicht verkneifen:

Die umgekehrte Herleitung der Funktionsgleichung aus dem Funktionsgraphen ist oftmals nötig, wenn es um Anwendungen geht. Beispielsweise steht an Gegenständen im Alltag ja meistens nicht ein Schild dran mit der Aufschrift

Oder wenn zwei Straßen miteinander verbunden werden sollen, ist erstmal noch gar nicht klar, mit welchen Kurven das möglich und sinnvoll ist:

Bei Anwendungen ergibt sich noch ein anderes Problem: da kommen oftmals Kurven vor, die nur ungefähr mathematischen Gesetzen gehorchen und deshalb durch Funktionsgraphen nur angenähert werden können. Und da stellt sich dann die Frage, wie (mit welchen Funktionen) man möglichst geringe Abweichungen der Funktionsgraphen von den vorgegebenen Kurven erreichen kann.

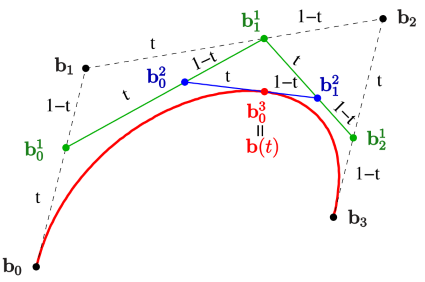
(Aber das ist eine Wissenschaft für sich. Vgl. etwa "Bézierkurven" und "Geometrische Modellierung".

Nebenbei: es ist doch merkwürdig, dass in den meisten Schulbüchern

• gar nicht [wie hier] begründet wird, weshalb man zu Graphen passende Funktionsgleichungen sucht,
• und auch nicht klar herausgestellt wird, dass die Umkehrung von ist.)

Aus einem Grund, der hier noch nicht verraten sei, möchte ich hier aber doch eine abstraktere Aufgabe behandeln

(Solche Aufgaben sind, wie wir noch sehen werden, teilweise einfach nur schwachsinnig und - so unterstelle ich mal dreist - nur dazu gedacht, Schüler zu quälen.)

Die Aufgabe habe ich nonchalant einem Schulbuch entnommen:

Bemerkenswert an dieser Aufgabe ist es allemal, dass da

• eben gerade nicht

(wie etwa bei )

eine durchgehende Kurve vorgegeben ist, zu der die Funktionsgleichung gesucht wird,

• sondern dass da nur isolierte Eigenschaften des Funktionsgraphen genannt werden

(es sei allerdings daran erinnert, dass wir oben auch "nur" wenige markante Punkte errechnet und daraus halbwegs den Graphen zusammengeschustert hatten).

scheint also ein Etikettenschwindel zu sein.

Die Aufgabe taucht aber dennoch hier im zweiten Teil auf, weil trotz aller Abstraktion die ganze Zeit

(außer bei "ganzrationalen Funktion 3. Grades")

vom (Funkions-)"Graph" die Rede ist und dazu aufgefordert wird, die noch unbekannte Funktionsgleichung zu bestimmen.

Die Aufgabe ist reine Mathematik und keine Anwendungsaufgabe, was zur Folge hat, dass wirklich jedes Detail der Aufgabe für unser Vorhaben, die Funktionsgleichung zu finden, wichtig ist:

1. "ganzrationale[n] Funktion 3. Grades":

Das bedeutet

1. algebraisch, dass die gesuchte Funktionsgleichung folgende Form hat: y = ax³ + bx² + cx + d ,
2. geometrisch, dass der Funktionsgraph eine -Form hat (s.o.).

Da muss A. wohl genauer erklärt werden:

mit y = ax³ + bx² + cx + d

(z.B. y = 3x³ + 9x² + 5x + 1 ),

(also z.B. [s.o.] oder ).

,

• Funktionenschar:   y = ax³ + bx² + cx + d ,
• einzelne Funktion: y = 3x³ + 9x² + 5x + 1 .

• auf einem Zahlenschloss gibt es für a , b , c und d nur die natürlichen Zahlen 0, 1, 2, 3, 4, 5, 6, 7, 8 und 9,
• während bei der Funktionenschar y = ax³ + bx² + cx + d für a , b , c und d
  • alle reellen Zahlen möglich sind

(also z.B. auch a = - 3,5 oder b = )

• außer a = 0 , denn dann liegt gar keine Funktion dritten, sondern z.B. nur noch eine Funktion zweiten Grades vor

(Beispiel: y = 0x³ + 9x² + 5x + 1 =

                    =           9x² + 5x + 1 ).

Bei der vorliegenden Aufgabe geht es nun darum,

• unter allen Funktionen der Funktionenschar y = ax³ + bx² + cx + d
• diejenige (Einzel-)Funktion zu finden, die die weiteren in der Aufgabe gestellten Bedingungen erfüllt

(also unten die Bedingungen b.A., b.B., c.A. und c.B.).

Also:

Hier im zweiten Teil ist ALLES andersrum als im ersten Teil :

• in
  • war die (Einzel-)Funktion mit der Funktionsgleichung y = x³ + 2x²   gegeben, waren also a =   und b = 2 schon bekannt
  • und waren die x-Werte markanter Punkte noch unbekannt und mussten sie erst errechnet werden,
• hier in hingegen
• sind die x-Werte markanter Punkte bekannt

2. „[...] deren Graph die x-Achse im Ursprung berührt [...]"

Schon hier wird deutlich, dass die vier Bedingungen im blau unterstrichenen Teil geradezu heimtückisch gut versteckt sind:

1.   „im Ursprung" bedeutet nämlich zu allererst, dass der Graph überhaupt durch den Ursprung geht, dass also U (0 | 0) auf dem Graphen liegt.

Obwohl vom Graphen die Rede ist, müssen wir doch die algebraische Konsequenz daraus ziehen:

U (0 | 0) liegt genau dann auf dem Graphen, wenn seine beiden Koordinaten 0 und 0 die Gleichung y = ax³ + bx² + cx + d erfüllen, wenn also gilt

0 = a•0³ + b•0² + c•0 + d

Da jetzt x und y nicht mehr vorkommen, können wir uns zum ersten Mal darum kümmern, nacheinander  a , b , c und d auszurechnen: 

Diese Rechnung war besonders einfach, weil der Funktionsgraph durch U (0 | 0) geht und damit wegen der Nullen fast alle Summanden in der Gleichng wegfällen

(die Autoren der Aufgabe waren also auch nett [Zucker] und nicht nur heimtückisch [Peitsche]).

Mit d = 0 sieht die Gleichung y = ax³ + bx² + cx + d nun aber so

                                                  y = ax³ + bx² + cx + 0

und dann so

                                                  y = ax³ + bx² + cx

aus, und ab sofort rechnen wir nur noch mit dieser Gleichung y = ax³ + bx² + cx weiter, vergessen wir also das d endgültig.

Von den ursprünglich vier Unbekannten  a , b , c und d sind also a , b und c übrig, und

 .

Kurze geometrische Überlegung: vom Funktionsgraphen haben wir bislang nur den Ursprung U (0 | 0) benutzt:

2. "[...] die x-Achse im Ursprung berührt [...]" bedeutet zusätzlich

(und wieder arg verklausuliert),

dass der Graph in U (0 | 0) eine waagerechte Tangente, dort also die Steigung 0 hat. Und wenn wir das wieder in Algebra übersetzen, folgt

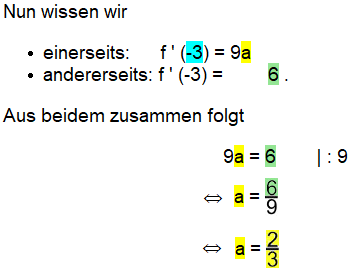
       f ' ( 0 ) = 0

(es sei daran erinnert: f ' zeigt die Steigung des Funktionsgraphen der Ausgangsfunktion f an).

Leiten wir die Funktion f: y = ax³ + bx² + cx also erstmal ab:

(Nebenbei:

• auch hier haben wir wieder x aus der Gleichung rausgeworfen;
• wir können den Aufgabenautoren wieder zutiefst dankbar sein, dass das Berühren im
Ursprung stattfindet, denn dadurch wird die Rechnung wegen der vielen Nullen auch dieses Mal besonders einfach.)

Wir wissen nun also

• einerseits:       f ' ( 0 )  =        0 ,
• andererseits:  f ' ( 0 ) =   c       .

Aus beidem zusammen folgt c = 0 , und wenn wir nun 0 für c in y = ax³ + bx² + cx einsetzen, erhalten wir

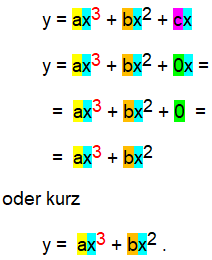
Ab sofort rechnen nur noch mit dieser Gleichung y =  ax³ + bx² weiter, vergessen wir also auch das c endgültig.

Von den ursprünglich vier Unbekannten  a , b , c und d sind inzwischen also nur noch a und b übrig, und

.

Kurze geometrische Überlegung: vom Funktionsgraphen haben wir inzwischen den Ursprung U (0 | 0) und die waagerechte Tangente dort:

3.  „[...] Tangente in P (-3 | 0 ) parallel zu y = 6x":

1. sollte es uns inzwischen schon gar nicht mehr überraschen, dass das eben auch bedeutet:

bzw.                                                                                    b = 3a    

Wenn wir in y = ax³  +  b x² für b nun 3a einsetzen, erhalten wir

                     y = ax³ + 3ax²

und damit eine Gleichung, in der von den vier ursprünglich gesuchten Unbekannten  a , b , c und d nur noch die Unbekannte  a  übrig ist:

Mit y = ax³ + 3ax² nähern wir uns aber langsam dem Ende unserer Überlegungen: weil da von den Unbekannten  a , b , c und d nur noch a übrig ist, werden wir gleich

(wenn wir auch noch x und y rauswerfen)

eine Gleichung haben, in der nur noch die einzige Unbekannte a vorkommt und die somit lösbar ist.

Hier müssen wir aber dringend festhalten: wir konnten zwar mittels b = 3a das b aus unseren Gleichungen rauswerfen

(und ab da nur noch mit a weiterrechnen),

aber das heißt nicht, dass wir damit schon wissen, welche Zahl hinter b steckt. b bleibt also vorerst eine Unbekannte.

Noch genauer: die Gleichung b = 3a zeigt zwar einen Zusammenhang zwischen a und b , aber damit kennen wir bislang weder den Zahlenwert von a noch den von b . Wir wissen nur, dass b drei Mal so groß wie a ist. Genau das werden wir unten aber noch zwei Mal brauchen können und dann auf Umwegen doch noch b berechnen.

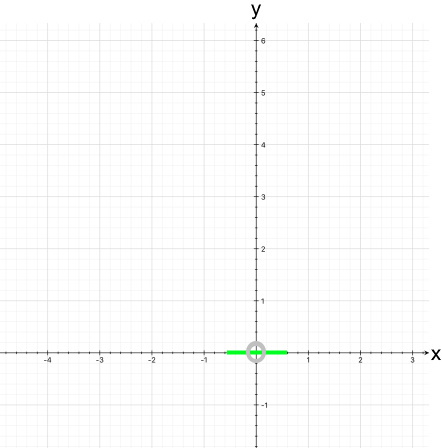
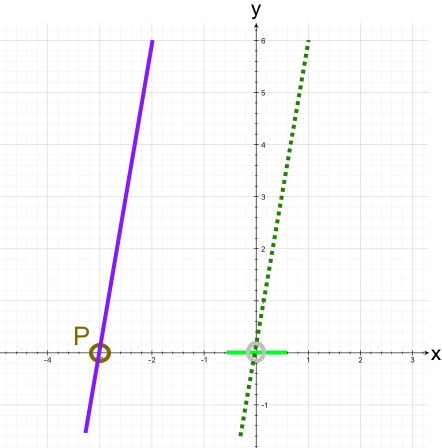
Kurze geometrische Überlegung: vom Funktionsgraphen haben wir jetzt zusätzlich den Punkt P (-3 | 0) :

2.  „[...] Tangente in P (-3 | 0 ) parallel zu y = 6x" ist für Schüler ansonsten doppelt und dreifach schwierig:

• sie müssen erkennen, dass y = 6x eine Geradengleichung ist.

• Wenn die Tangente in P parallel zu y = 6x ist, so ist hier daran nur interessant, dass die Tangente dieselbe Steigung wie die Gerade mit der Funktionsgleichung y = 6x hat. Die Steigung dieser Geraden ist aber 6.

Die Tangente in P (-3 | 0) hat also die Steigung 6.

(Warum aber sagen die Schulbuchautoren das dermaßen um drei Ecken?)

Wenn wir nun auf die Aufgabenstellung zu antworten, also die gesuchte Funktionsgleichung anzugeben versuchen, stellen wir fest, dass wir

• inzwischen zwar   a , c und d kennen

(nämlich a = , c = 0 und d = 0 ),

• aber noch immer nicht b , das uns bei all dem Rumjonglieren mit Gleichungen irgendwo abhanden gekommen ist.

Wir können bislang also nur sagen, dass die gesuchte Funktionsgleichung die Form

y = x³ + bx² + 0x + 0

bzw.

y = x³ + bx²

hat.

Nun haben wir aber sämtliche Vorgaben der Aufgabe bereits benutzt, in der Aufgabenstellung ist also keine Hilfe mehr zu erwarten, um zuguterletzt auch noch b zu berechnen.

Deshalb müssen wir uns erinnern, wo wir denn b verloren bzw. wo es in all unseren Rechnungen zum letzten Mal vorgekommen ist. Das aber war bei

 b = 3a   

der Fall, also jener Gleichung, mit der wir b zwischenzeitlich aus unseren Gleichungen rauswerfen konnten (so dass nur noch a übrig blieb).

Wenn wir nun aber in diese Gleichung  b = 3a für a den inzwischen bekannten Wert einsetzen, erhalten wir b = 3• , also b = 2  

(... womit die Gleichung b = 3a zum zweiten Mal für uns nützlich geworden und somit die vielleicht wichtigste Gleichung all unserer Überlegungen ist).

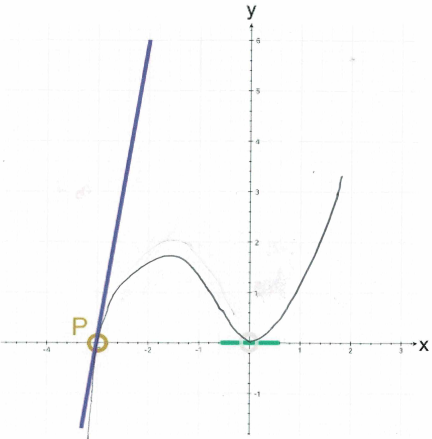
Damit können wir nun ENDLICH vollständig auf die Aufgabenstellung antworten:

die gesuchte Funktionsgleichung ist y = x³ + 2x² 

Und jetzt endlich können wir auch sagen:

Bemerkenswert ist hier vielleicht auch noch, dass wir der Aufgabenstellung zwar einige markante Punkte des Graphen entnommen haben, aber noch immer nicht wissen, wie dieser Graph vollständig aussieht.

Wir konnten also erstaunlicherweise aus einigen wenigen Eigenschaften des Graphen auf seine Funktionsgleichung y = x³ + 2x² schließen.

Kleine geometrische Anmerkung: weil die Gerade g mit der Funktionsgleichung y = 6x die Steigung 6 hat, haben wir vom Funktionsgraphen nun zusätzlich die zu der Geraden g parallele Tangente t mit der Steigung 6:

Mit

• diesen Informationen,
• dem Wissen, dass eine Funktion dritten Grades vorliegt, der Graph also eine -Form hat,
• und einiger Phantasie

Vor lauter ellenlangen Rechnungen mag es einem entgangen sein, dass

• am Anfang des ersten Teils
• und am Ende des zweiten Teils 

dieselbe Funktionsgleichung stand, nämlich y = x³ + 2x² .

Wir haben also oben

• in
  • zu der Funktionsgleichung y = x³ + 2x²
  • die markanten Punkte errechnet
  • und durch diese den Funktionsgraphen  gezeichnet,
• umgekehrt in
  • aus markanten Punkten des Funktionsgraphen
  • die Funktionsgleichung y = x³ + 2x² hergeleitet. 

Dieses Hin und Her war für mich gerade der Grund,

• im ersten Teil die ungewöhnliche Funktionsgleichung y = x³ + 2x²

(also ohne Rattenschwanz; s.o.)

• und im zweiten Teil die herrlich bescheuerte Aufgabe zu nehmen.

Bevor aber jemand immer nur noch vor der Glotze oder dem Computer dahinvegetiert, kann er gerne wochenlang

y = x³ + 2x²  und

immer wieder hin und her ineinander umwandeln, bis er ähnlich matschig in der Birne ist wie nach wochenlangem Konsum von "Privatfernsehen":

Schon allein die Länge der obigen Ausführungen macht deutlich, dass die Aufgaben für Schüler keineswegs leicht sind

(zumindest bei den ersten Aufgaben dieser Art):

die Lösung der Aufgaben erfordert

• eine enorme Menge an Vorwissen,
• ein wohlüberlegtes Vorgehen in der (einzig) richtigen Reihenfolge,
• ein großes Vorstellungsvermögen

(solange nicht einfach nur ein stumpf eingepauktes, aber unverstandenes "Schema F" runtergespult wird)

• und verlässliche Rechenfertigkeiten.

Nicht eingehen möchte ich hier auf die Frage, ob solche Aufgaben wie die oben gelösten überhaupt sinnvoll sind, wobei ich mit "sinnvoll" nicht eine (fragliche) Anwendbarkeit meine, sondern ob Schüler beim Lösen solcher Aufgaben etwas innermathematisch Sinnvolles lernen.

Noch kurz möchte ich hingegen auf die Anwendung zurück kommen, die so ähnlich auch in dem Schulbuch vorkommt, aus dem ich die Aufgabe geklaut habe.

Dort allerdings lautete die Rutschen-Aufgabe:

Das ist ja durchaus eine schöne Aufgabe

(wenn man mal von der viel zu frühen "mundgerechten" Mathematisierung absieht [Koordinatensystem, Punktkoordinaten, Definitionsbereich]).

Was mich allerdings gewaltig stört, ist,

• dass da vorausgesetzt wird, dass die Rutsche in den Punkten A und B waagerecht ist, also die Steigung null hat (wieder so eine zu frühe Mathematisierung),
• statt dass mal überlegt wird, warum das bei vielen Rutschen so ist, ob das also sinnvoll ist. Vgl. etwa auch

.

Ich will diesen "Sinn" hier gar nicht verraten, aber man stelle sich mal vor, die Rutsche sähe so aus:

Da kann ich nur sagen: arme Kinder!

Besser als die staubtrockene Schulbuchaufgabe

ist es zweifelsohne, mit den Schülern mal - horribile dictu! - aus der Schule raus und auf den erstbesten Spielplatz mit Kinderrutsche zu gehen!

(... und zwar ohne den Schülern vorweg zu verraten [!], dass heute dran ist, und auch nicht, welche Funktionenklasse für die Modellierung einer Rutsche am besten geeignet ist.

Man nehme mehrere mit.

Es wäre aber auch eine schöne Hausaufgabe, wenn die Schüler mal eine Rutsche auf einem Spielplatz in der Nähe ihrer Wohnung vermessen würden

[Arbeitsanweisung an die Schüler: "Liebevoll mit den Kinder auf dem Spielplatz umgehen, nichts beschädigen oder verdrecken, basta!"]

Solch eine Rutsche wäre mir da allemal auch willkommen, denn da stellt sich doch die Frage: "Was bewirkt der Buckel in der Mitte bzw. was daran macht Kindern besonderen Spaß?"

Ein interessantes Thema wäre da auch die Messung der Geschwindigkeit[en], was heute mit Film-Einzelbildern durchaus möglich sein müsste:

  →  )

Lösen nach Schema F

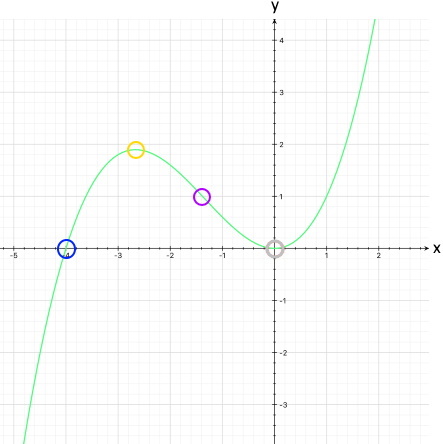
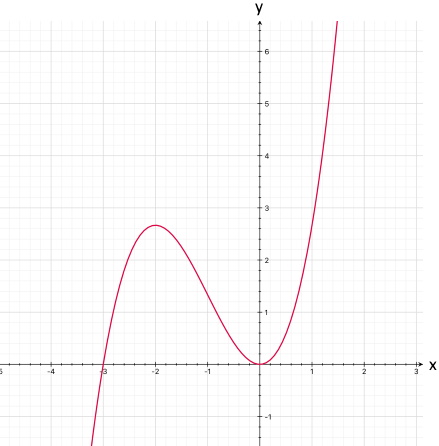
Gegeben ist der Funktionsgraph 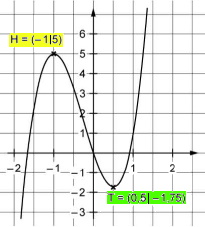, gesucht ist die Funktionsgleichung der zugehörigen Funktion dritten Grades.

"
Funktion dritten Grades" bedeutet, dass die Funktionsgleichung so aussehen muss:

y = ax³ + bx² + cx + d

Das ist die Gleichung der Schar aller (also unendlich vieler) Funktionen dritten Grades, und wir suchen

• unter all diesen Funktionen jene (einzige), die die Vorgaben des Graphen erfüllt,

• also die passende Zahlenkombination von  a , b , c und d .

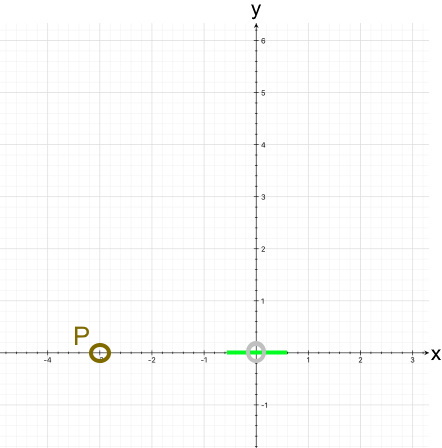
Nutzen wir also die einzigen Informationen, die der Funktionsgraph hergibt, nämlich H ( -1 | 5 ) und T (0,5 | -1,75 ). Das sind aber anscheinend nur zwei Informationen, also zu wenig.

In Wirklichkeit enthält aber jede der beiden Informationen zwei Informationen:

• zu H ( -1 | 5 ) :

• zu T (0,5 | -1,75 ) :

Schauen wir uns nun also an, was die soeben gefundenen vier Bedingungen rechnerisch bedeuten:

zu 1.: H ( -1 | 5 )

• liegt genau dann auf dem Funktionsgraphen,
• wenn seine beiden Koordinaten x = -1 und y = 5
  

• d.h. wenn gilt:

zu 2.: H ( -1 | 5 )

(die eigentlich sonst noch nötige zweite Ableitung brauchen wir hier glücklicherweise nicht;

und ebenso wenig brauchen wir hier den y-Wert 5 ).

Dazu bilden wir kurz die erste Ableitung:

     f   ( x ) =   a   x³    +   b   x² + cx + d

⇒ f ´ ( x ) = 3a   x²   + 2b   x    + c

⇒ f ´ (-1) = 3a•(-1)² + 2b•(-1)  + c

Da wir wissen, dass  f ' ( - 1) = 0 sein muss, gilt also

zu 3.: T (0,5 | -1,75 )

zu 4.: T (0,5 | -1,75 )

• ist ein Tiefpunkt,

• wenn dort die Steigung 0 ist, wenn also f ' ( - 0,5 ) = 0 ist,

• d.h. wenn gilt

              D.         0     = 3a•(-0,5)² + 2b•(-0,5)  + c

Mit A. , B. , C. und D. haben wir nun unsere gesuchten vier Gleichungen

(und können den Funktionsgraphen endgültig vergessen - und nur noch rechnen).

Schreiben wir nun die Gleichungen A. , B. , C. und D. schön übersichtlich direkt untereinander:

           A.         5        = a•(-1)³ + b•(-1)² + c•(-1) + d

          B.         0 .      = 3a•(-1)² + 2b•(-1)  + c

          C.         -1,75 = a•(0,5)³ + b•(0,5)² + c•(0,5) + d

  D.         0       = 3a•(-0,5)² + 2b•(-0,5)  + c

Nun haben die Mathematiker sich darauf geeinigt, die hier bislang immer einsam links vor Gleichheitszeichen stehenden Zahlen immer rechts nach dem Gleichheitszeichen zu schreiben, also die beiden Seiten der Gleichungen auszutauschen:

          A.         a•(-1)³ + b•(-1)² + c•(-1) + d       = 5

          B.         3a•(-1)² + 2b•(-1)  + c                 = 0

          C.         a•(0,5)³ + b•(0,5)² + c•(0,5) + d = -1,75

  D.         3a•(-0,5)² + 2b•(-0,5)  + c           = 0

Wenn wir nun in allen Gleichungen die Terme weitestmöglich vereinfachen, erhalten wir

          A.       -  a + b - c + d                      = 5

          B.         3a - 2b + c                         = 0

          C.       0,125a + 0,25b + 0,5c + d = -1,75

  D.         0,75a - b + c                      = 0

Und wenn wir jetzt noch die Variablen hübsch ordentlich untereinander schreiben, ergibt sich

          A.              -  a +        b -        c + d  = 5

          B.               3a -       2b +       c        = 0

          C.       0,125a + 0,25b + 0,5c + d = -1,75

  D.         0,75a -          b +      c        = 0

Falls einen in den Gleichungen C.  und  D. die Dezimalbrüche stören, kann man noch

•        in C. die beiden (!) ganzen (!) Seiten der Gleichung mit 8
• und in D. die beiden (!) ganzen (!) Seiten der Gleichung mit 4 multiplizieren

und erhält dann

          A.              -  a +        b -        c +   d  =    5

          B.               3a -       2b +       c          =    0

          C.                a +       2b +    4c + 8d = -14

  D.              3a -        4b +     4c         =    0

Jede dieser vier Gleichungen ist unlösbar, da in jeder Gleichung mehrere Unbekannte vorkommen. In jeder Gleichung bekommen wir also nur Abhängigkeiten der Unbekannten voneinander.

(Ein Beispiel: Anna, Berta und Carla sind zusammen drei mal so groß wie Dora - bzw. a + b + c = 3 • d.

• In dem Satz bzw. der Gleichung sind vier Unbekannte enthalten, und damit wissen wir noch keineswegs, wie groß Anna, Berta, Carla und Dora sind.
• Und selbst wenn wir die Größe von Dora wüssten, blieben noch immer drei Unbekannte, wüssten wir also noch immer nicht die Größen von Anna, Berta und Carla.
• Wenn wir zusätzlich noch die Größe von Carla wüssten, blieben noch immer zwei Unbekannte, wüssten wir also noch immer nicht die Größen von Anna und Berta.
• Erst wenn wir dann noch die Größe von Berta erfahren,  bleibt nur noch eine Unbekannte [Annas Größe], die wir dann aber berechnen könnten.)

Aber im Viererpack , also zusammen, sind die vier Gleichungen sehr wohl lösbar

(Es sei daran erinnert, dass man eine Kombination mehrerer Gleichungen mit mehreren Variablen „Gleichungssystem“ nennt.)

Man kann ein Gleichungssystem auf zwei Arten lösen:

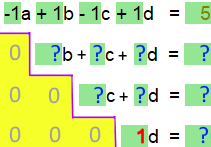1. händisch, wobei dringend das ziemlich idiotensichere, allerdings mit viel Schreibarbeit verbundene Gaußsche Dreiecksverfahren empfohlen sei, um Übersicht im Zahlendschungel zu behalten.
2. mit einem Graphischen Taschenrechner oder Computer, wofür allerdings Nullen und Einsen zu ergänzen sind:

          A.              -1a + 1b - 1c + 1d  =    5

          B.               3a -  2b + 1c + 0d  =    0

         C.               1a + 2b + 4c + 8d  = -14

  D.               3a -  4b + 4c + 1d  =    0

Für die Eingabe in den Computer interessieren nun gar nicht die Unbekannten a , b , c und d , sondern nur die Zahlen mit Vorzeichen vor den Unbekannten, also

          A.              -1a + 1b - 1c + 1d   =    5

          B.               3a -  2b + 1c + 0d  =    0

         C.               1a + 2b + 4c + 8d  = -14

  D.               3a -  4b + 4c + 1d  =    0

Wenn man nun diese Zahlen in den Computer eingibt, erhält man dann aber doch die Ergebnisse für die Unbekannten  a , b , c und d .

Weder die händische noch die Computer-Lösung sei hier aber vorgemacht, sondern nur die Ergebnisse angegeben:

          A.              a =    4

          B.              b =    3

         C.              c  = - 6

  D.              d  =   0

Eingesetzt in die Funktionenschargleichung y = ax³ + bx² + cx + d ergibt sich somit

die gesuchte       Funktionsgleichung            y = 4x³ + 3x² - 6x + 0

oder kurz                                                           y = 4x³ + 3x² - 6x .

Angenommen, ausgehend vom Funktionsgraphen einer (quadratischen) Funktion zweiten Grades wird die zugehörige Funktionsgleichung gesucht.

Dann muss diese Funktionsgleichung Element der Funktionenschar y = ax² + bx + c sein.

• Es sind also die 2 + 1= drei Unbekannten  a , b und c zu berechnen,
• wozu wir dem Funktionsgraphen drei Bedingungen entnehmen
• und diese in drei Gleichungen umsetzen müssen,
• die zu einem Gleichungssystem aus drei Gleichungen mit drei Unbekannten führen,
• mit dem wir dann die drei Unbekannten a , b und c berechnen können
• und damit die Funktionsgleichung erhalten.

Allgemein gilt für eine gesuchte Funktionen n-ten Grades:

        Funktionsgraph → dem Graphen n+1      Bedingungen für n+1      Unbekannte entnehmen

                                   → Gleichungssystem aus   n+1   Gleichungen mit n+1     Unbekannten → Lösungen für die n+1     Unbekannten → Funktionsgleichung.

Also z.B.         für eine                  Funktion     6-ten Grades:

                                   → Gleichungssystem aus 6+1=7 Gleichungen mit 6+1=7 Unbekannten → Lösungen für die 6+1=7 Unbekannten → Funktionsgleichung.