
Gottfried Wilhelm Leibniz, 1646-1716, benutzte den Begriff "functio" als erster im heutigen mathematischen Sinne (vgl.
)
Zuordnungen, Funktionen und Funktionenscharen
|
|
![]() Einleitung
Einleitung
![]() Zuordnungen
Zuordnungen
![]() Funktionen
Funktionen
![]() Funktionenscharen
Funktionenscharen
| Sinusoïde C'est fatigant dans les montées |
|
| E. Guillevic, Euclidiennes | |
vgl. auch ![]() Funktionen ... fühlen!
Funktionen ... fühlen!
Es reicht allerdings auch ein ganz normales Schultreppengeländer, Hauptsache, es ist nicht neumodisch weitgehend stückweise linear mit einigen Knicken. Sondern man suche sich einen schön elegant geschwungenen, handschmeichlerischen "Handlauf" (!).
An das Schultreppengeländer lasse man die SchülerInnen nun mittels Tesakrepp alle Eigenschaften dranschreiben, also "Wendepunkt", "Linkskurve" usw.
Probleme bzw. eher Herausforderungen können sich allerdings ergeben,
wenn das Geländer durch mehrere Stockwerke läuft, sich also übereinander wiederholt, d.h. keine Funktion darstellt: dann definiere man (mit Tesakrepp) eben abschnittsweise Funktionen;
dass das Geländer dreidimensional ist: dann gibts eben von der Seite gesehen andere Wendepunkt als von oben gesehen.
| Es kann kein Zweifel bestehen, dass Funktionen einer der Zentralbegriffe nicht nur der Schul-, sondern auch der gesamten Mathematik sind. |
Alle Klarheiten beseitigt?
Das ja eben ist das alte Leid nicht nur mit den Fach-, sondern auch mit den Universallexika, die doch eigentlich - sicherlich ausgehend von einer gewissen Grundbildung - eine erste Orientierung zu bislang Unbekanntem geben soll(t)en: um etwas zu verstehen, muss man schon alles verstanden haben.
Der Lexikonartikel ist - wenn überhaupt - nur dienlich als Verweis auf eingehendere Mathematikbücher. Aber da greife ein Laie doch besser gleich zu solchen Büchern.
Mir scheint, man hatte mal wieder Angst vor einer halbwegs anschaulichen, damit aber auch evtl. fachterminologisch unsauberen Einführung.
Also einfacher und anschaulicher:
Die meisten der im Folgenden gezeigten graphisch-anschaulichen Eigenschaften müssten natürlich auch rechnerisch durchdrungen bzw. bewiesen werden (was in der Mittelstufe ja auch schon teilweise geschehen ist). Aber ich vertraue darauf,
|
- oftmals weniger für Einzelwerte
(das Lieblingskuscheltier eines Kindes),- als für ganze Serien von Werten
(die Lieblingskuscheltiere vieler/aller Kinder),- insbesondere für die Beziehungen von Werten zueinander
(z.B. enthält eine Weinflasche 11% Alkohol, und zwar, egal wie groß die Weinflasche und also auch die Alkoholmenge in ihr ist)Die Mathematik interessiert sich also weniger für die "Dinge" (die nummeriert sie einfach mit Zahlen durch) als für ihre Beziehungen zueinander, also sozusagen für den

Bzw. die Einzel"dinge" interessieren oftmals nur insoweit, als sie sich zueinander verhalten.
(Genauso könnte man sagen: ein Mensch wird erst definiert durch sein Verhältnis zur Umwelt und zu Mitmenschen, und ohne sie ist er nichts.)
Und da interessieren sich MathematikerInnen insbesondere für Beziehungen, die nach einer klaren Ordnung verlaufen
(vgl. unten Zuordnung, die "Regel" und die Zuordnungsvorschrift).
MathematikerInnen unterstellen also eine geordnete, klare Welt - statt einer willkürlich chaotischen
(wenn sie paradoxerweise sogar auch für den Zufall und das Chaos Modelle entwickelt haben).
Man könnte auch sagen:
Mathematik ist die Wissenschaft von den geordneten Beziehungen
Alles, was jenseits dieser geordneten Beziehungen liegt, interessiert MathematikerInnen nicht
(zumindest nicht solange sie Mathematik betreiben; aber vielleicht durchaus als Privatmenschen)
bzw. darüber können sie (als MathematikerInnen) nichts sagen.
(Einige MathematikerInnen mit Angst vor der Farbigkeit, aber auch Unvorhersehbarkeit der Welt [also Angst vor dem Leben!] leugnen dann aber einfach, dass es das Ungeordnete und Irrationale bzw. eine andere als die rein mathematische Logik [z.B. die Logik Bilder, Intensitäten und Assoziationen] überhaupt gibt.)
Ein Mittel, um Ordnung zu schaffen oder abzubilden, sind Zuordnungen und Funktionen.
Menge der
durchnummerierten SchülerInnen einer Klasse
{1;2 ... 27}
(Definitionsmenge)
wird zugeordnet
Menge der Schuhgrößen
{37;38 ... 49}
(Wertemenge)
x |→ y Schüler 1 |→ Schuhgröße 41 Schüler 2 |→ Schuhgröße 38 Schüler 3 |→ Schuhgröße 37 ...
- jedem Kind sein Lieblingskuscheltier,
- jedem BMW-Fahrer seinen Intelligenzquotienten,
- jedem Schüler seine Schuhgröße,
- jeder Schuhgröße all jene Schüler, die diese Schuhgröße haben
- ...
aber
Mathematiker interessieren sich vor allem für Zuordnungen von Zahlen zu Zahlen. (Selbstverständlich geht durch die Reduktion auf reine Zahlen viel verloren, ja wird Mathematik potentiell gemeingefährlich. Vgl.
)
Dabei ist klar: Mathematik kann vieles behandeln, aber nicht alles. Z.B. kann Mathematik zwar erstaunlicherweise die Planetenbahnen und die Formen der Planeten (z.B. die Ringe des Saturn) erklären
(und nicht mal das können sie absolut exakt, sondern nur die gegenseitige Anziehung zweier Körper; für mehr als zwei Körper [geschweige denn für die Sonne, ihre neun Planeten und deren Monde] haben sie aber immerhin erstaunlich gute Annäherungen),
aber niemals ihre anrührende Schönheit.
Dennoch ist es erstaunlich, wie viel mathematisch erfassbar ist, nämlich z.B.
- ein komplettes Fußballspiel (außer seiner Dramatik) durch
- die Position des Balls (Länge, Breite, Höhe bzgl. des Spielfeldmittel- bzw. Anstoßpunkt),
- den Zeitpunkt:
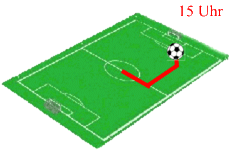
Ein "Tor" liegt dann vor, wenn der Ball zur richtigen Zeit (also weder vor noch nach dem Spiel) in der richtigen Position (im Netz) ist;
Farben:
weil jede Farbe aus den Grundtönen rot, grün und blau zusammenmischbar ist, kann man jede Farbe - wie Computer es tun - durch die Anteile dieser Grundtöne bestimmen (die hier zwischen 0 und 255 angegeben werden).Z.B.
ist
darstellbar als RGB (228|46|227)
Schwarz als RGB (0|0|0)
Weiß als RGB (255|255|255)
Zudem hat die Behandlung nackter Zahlen den entscheidenden Vorteil, dass Erkenntnisse auf viele Beispiele anwendbar und übertragbar sein können (worin der eigentliche Grund für den enormen Erfolg der Mathematik liegt). Z.B. kann die reine Zahlen-Zuordnung
1 |→ 37
2 |→ 40
erstens bedeuten:
Schüler 1 hat Schuhgröße 37
Schüler 2 hat Schuhgröße 40
zweitens:
Schüler 1 hat normale Körpertemperatur (370 C)
Schüler 2 hat hohes Fieber (400 C)
drittens:
Fußballstar 1 ist 37 Jahre alt
Fußballstar 2 ist 40 Jahre alt
...
x  y
y
Von besonderem Interesse ist, wie sich y ändert, wenn man x vergrößert. Z.B.:
- Wie verändert sich y, wenn ich x verdopple? Wird dann auch das y verdoppelt?
(Womit eine proportionale Funktion vorläge.)
Oder nimmt bei steigendem x das y ab?
Oder tut bei steigendem x das y mal das eine (zunehmen), mal das andere (abnehmen) - und warum?- Wie verändern sich die politischen Einstellungen (hin zur CDU und FDP?), wenn jemand Karriere macht, also mehr Geld verdient (also auch mehr zu verlieren hat)?
Grafisch werden die x-Werte im Koordinatensystem immer auf der waagerechten x-Achse aufgetragen und die y-Werte immer auf der senkrechten y-Achse (vgl. auch
).
Die Betrachtung eines Funktionsgraphen findet immer für wachsende x statt, d.h. der Graph wird grundsätzlich von links
nach rechts
"gegangen" (und nie umgekehrt!).
(Deshalb ja auch zeigt der Pfeil an der x-Achse nur nach rechts, obwohl die x-Achse natürlich nach beiden Seiten ins Unendliche geht.)

Im vorliegenden Fall steigt der Berg also anfangs bis zur Spitze, weil mit dem wachsenden x auch das y wächst.
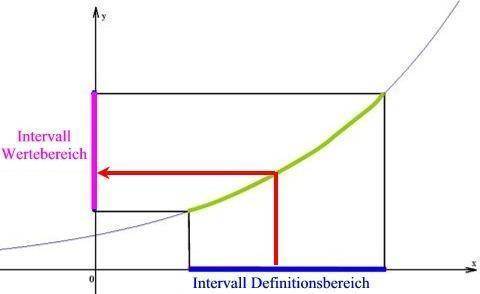
Wenn kontinuierliche Intervalle vorliegen, ist es auch sinnvoll, vom Definitions- und Wertebereich zu sprechen
(wenn man aus dem Wort "Menge" noch eher eine Ansammlung von getrennten Einzeldingen [die Rosinen in einem Teig], aus dem Wort "Bereich" aber eine homogene Masse [den Teig] heraus hört).
Schüler |→ Schuhgröße
uninteressant, weil
- sich weder aus der Schuhgröße des Vorgängers die Schuhgröße des Nachfolgers
- noch aus der Schülernummer x seine Schuhgröße y
berechnen lässt.
Sondern
Mathematiker lieben Zuordnungen, die in allen Fällen nach einer einzigen Regel verlaufen, mittels derer man zu jedem x sein zugehöriges y berechnen kann. Ein Beispiel:
Weil sonntags nachmittags die Züge von Köln nach Kiel mit Bundeswehrsoldaten überfüllt sind, die wieder zu ihrer Einheit müssen, setzt die Bahn Zusatzzüge ein, also z.B. zusätzlich zum Zug X noch einen Zug Y, der immer 20 km vor dem Zug X fährt:
y = x + 20
wobei y der Ort des Zuges Y und x der Ort des Zuges x ist.
Geregelte Zuordnungen stellen
- eine (!) allgemeine Regel auf,
- einen (!) prinzipiellen Zusammenhang dar
(der noch unabhängig vom Einzelfall ist bzw. für jeden der unendlich vielen möglichen Einzelfälle gilt).Wichtig dabei ist, dass diese Regel immer gilt, egal, wo der Zug X sich gerade befindet:

Setzt man in die Zuordnung/Regel konkrete Werte ein, so erhält man
- einen Spezialfall,
- einen Punkt bzw.
- ein Standbild.
Wenn man nun für x konkrete Orte einsetzt, so erhält man das jeweils zugehörige y :
Leverkusen = Köln + 20
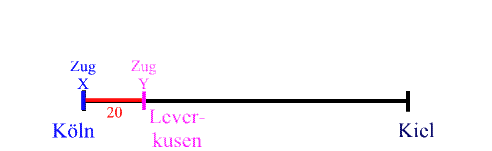
Dortmund = Bochum + 20
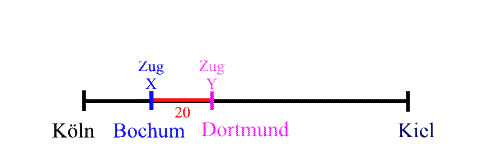
(Eigentlich müßig zu ergänzen, dass hier schon erheblich abstrahiert, nämlich von - insbesondere bei Bahnhöfen eintretenden - Brems- und Beschleunigungsmanövern abgesehen wurde.)
Dennoch scheint es mir äußerst zweifelhaft, dass in der Schulmathematik immer nur fertige Funktionen durchgenommen werden, d.h. dass üblicherweise erst die Regel (Zuordnungsvorschrift bzw. Funktionsgleichung) feststeht und dann aus ihr automatisch der Graph folgt:
sieht jede Anwendung ganz anders aus: beispielsweise steht am freien Fall ja nicht die Formel "s = 1/2gt2" dran, sondern diese Gleichung ist überhaupt erst zu finden
(ja es ist nicht mal so selbstverständlich, dass die Natur sich überhaupt nach einer mathematischen Formel verhält).Im Unterricht werden viel zu selten "Messpunkte" genommen, zu denen überhaupt erst eine (annähernde!) Gleichung zu finden ist
Bzw. wenn überhaupt, so werden "Steckbriefaufgaben" behandelt, bei denen aus gewissen Eigenschaften (Punkten, Verhalten) auf die von Anfang an gemeinte und eindeutige Funktion zurück geschlossen werden muss.
ist "in der freien Wildbahn" üblicherweise die Zukunft offen
(während in der Mathematik immer schon klar ist, wie es weitergeht: wenn z.B. der Graph von y = x2 jetzt noch fällt, wird er demnächst auch wieder steigen),
und im besten Fall deuten sich Trends an:
Es ist wie eine Bergwanderung im Nebel, bei der man nie verlässlich weiß, wie es weiter geht:
Solche "Offenheit" scheint mir durchaus auch innermathematisch bedeutsam: wie sonst soll denn anschaulich klar werden, was beispielsweise ein Wendepunkt ist - nämlich ein Trendwechsel (und damit vielleicht wichtiger als solch kurzfristige Verheißungen bzw. Enttäuschungen wie Maxima und Minima).
y =
,
wobei das Kästchen für die Standardregel steht, mittels derer man zu jedem x sein zugehöriges y erhält. Man kann sich das Kästchen auch als eine Maschine vorstellen, die aus jedem x automatisch sein zugehöriges y macht:
x rein →
→ y raus
Solch eine Funktionsmaschine ist
- bienenfleißig bzw. absolut geistlos, weil sie jedes x aus dem Definitionsbereich "frisst" (oftmals unendlich viele),
- meistens absolut wahllos
(Manchmal aber "verschlucken" sich solche Funktionsmaschinen und speien dann mit Riesengetöse all ihre Zahnräder aus; z.B. - igitt! - bei einer Division durch 0. Woraus folgt: man bedenke immer vorher, was man überhaupt in die Maschine eingeben darf).
Um zu verdeutlichen, was da geschieht, wird ab spätestens hier
- das x immer blau,
- die Maschine/Regel immer rot
- und das sich
- aus x
- mittels der Maschine/Regel
ergebende y immer violett (also mit der Mischfarbe
aus blau und rot) dargestellt.
Ein Beispiel ist die (egal was)hoch 3-Maschine:
| Ausgangsmaterial x | Maschine | Fertigprodukt y |
Diese (egal was)hoch 3-Maschine verarbeitet nun sämtliche reellen Zahlen in ihre zugehörigen y-Werte, also z.B. x = 5:
Und dann gibt es noch
Großmaschinenwie z.B. y =
, bei der mehrere Arbeitsschritte (Zahnräder) hintereinander liegen, um das x vielfach zu bearbeiten, bevor am Ende y rauskommt. Aber auch diese Maschinen machen mit allen x stumpf dasselbe nach einer Regel.
Typische Regeln sind z.B.:
- bevor die Menschen sich ins Bett des Prokrustes legen
Prokrustes [...], in der griech. Mythologie ein riesenhafter Unhold, der Vorbeiziehende durch Abhacken bzw. Strecken ihrer Glieder in ein Bett einpaßt [...]
© Meyers Lexikonverlag ,sind sie unterschiedlich groß, nachher nicht mehr:

womit eine linear-konstante Funktion vorläge, weil allen unterschiedlichen anfänglichen Körpergrößen x dieselbe spätere Länge y zugeordnet würde; man könnte auch sagen: konstante Funktionen sind die "ausgleichende Gerechtigkeit": "take it from the rich, give it to the poor")
- für niemanden wird mehr eine "Extrawurst gebraten", sondern alle werden radikal gleichbehandelt;
- es gibt keine unterschiedlichen Steuersätze mehr, sondern jede Person x zahlt 15 % von seinem jeweiligen Einkommen als Steuer;
(wie alle Funktionen, die Prozente behandeln, eine linear-proportionale Funktion: wenn jemand das n-fache verdient, muss er auch n-mal soviel Steuern bezahlen)- schäle egal welche (große, kleine) Kartoffel x solange, bis eine (große, kleine) geschälte Kartoffel y dabei herauskommt
- y = x2 , d.h. quadriere gnadenlos jedes x
- y = 5●x, d.h. multipliziere gnadenlos jedes x mit 5.
(Solch eine Vielzahl von Eigenschaften lässt sich später durchaus mit sogenannten Vektoren erfassen.)
Unter der Voraussetzung, dass niemand zwei Schuhgrößen gleichzeitig hat, ist also die Zuordnung
Schüler |→ Schuhgröße
eindeutig
(wobei durchaus mehrere Schüler dieselbe Schuhgröße haben dürfen).
(Nebenbei: die Zuordnung Schüler |→ Schuhgröße kann man notfalls auch dann eindeutig machen, wenn einige SchülerInnen jeweils zwei verschieden große Füße und damit unterschiedliche Schuhgrößen haben. Dann grenzt man eben - ein typisches Verfahren - den Definitionsbereich
auf diejenigen SchülerInnen ein, die jeweils gleichgroße Füße und damit eine Schuhgröße haben, d.h. man lässt die anderen SchülerInnen einfach probeweise weg.)
Die umgekehrte Zuordnung
Schuhgröße |→ Schüler
ist aber üblicherweise nicht eindeutig, denn zu jeder Schuhgröße kann es mehrere Schüler mit dieser Schuhgröße geben
(man weiß insbesondere dann, wenn alle Schuhe gleich aussehen, nicht mehr, wem welche Schuhe gehören).
Zuordnungen, die auf dem gesamten Definitionsbereich eindeutig sind, nennt man auch "Funktionen". "Ein Gerät funktioniert nicht, wenn etwa beim Betätigen einer Taste gar nichts oder nicht das Gewünschte geschieht, etwa die falsche Lampe aufleuchtet. Wir erwarten also wie bei einer Maschine auf eine bestimmte Eingabe eine eindeutig bestimmte Ausgabe, und damit ist dann schon etwas Typisches des Funktionsbegriffs angesprochen: die eindeutige Zuordnung."
(zitiert nach)
Stellen wir uns also eine Funktion als ein Gerät vor, das eindeutige Ergebnisse liefert - also z.B. eine Fußgängerampel:
Sie kann (übereinander!) entweder nur rot oder nur grün, nie aber gleichzeitig rot und grün anzeigen
(eine Autoampel
wäre hier eine schlechte Illustration wäre, weil sie gleichzeitig rot und gelb sein kann [kurz bevor es grün wird]).
Graphisch erkennt man Funktionen daran, dass
- sie niemals parallel zur y-Achse verlaufen:
- sie niemals zurück (erst nach rechts und dann wieder nach links bzw. umgekehrt) laufen:
- niemals mehrere Punkte übereinander liegen:
MathematikerInnen biegen sich "die Welt" notfalls solange zurecht, bis sie ihnen "in den Kram" passt. Wenn z.B. die Zahlen y gesucht werden, deren Quadrat 9 ist, also
y = 3
y2 = 3 2 = 9
y = (-3)
y2 = (-3)2 = 9,
so gibt es offensichtlich zu dem einen 9 zwei y, nämlich y = 3 oder y = -3, und somit ergibt sich insgesamt als Graph
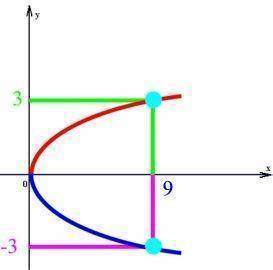
Hier liegt aber offensichtlich keine Funktion vor, weil zwei Punkte übereinander liegen. Deshalb lassen die MathematikerInnen einfach den unteren Ast des Graphen weg, und schon erhalten sie einen Funktionsgraphen:
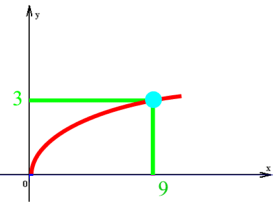
Die Vereinfachung (Funktion) hat allerdings auch eine Erschwernis zur Folge: weil als Wurzel von 9 nur noch die positive Zahl 3 erlaubt ist, ist ab sofort immer eine Fallunterscheidung nötig, um dennoch beide Lösungen zu erfassen.
y2 = 9
y = +
oder y = -
y = + 3 oder y = - 3
y = 3 oder y = - 3
Es gibt
umkehrbare Funktionen, d.h. die umgekehrte Zuordnung ist auch wieder eine Funktion. Z.B. sind
y = 2 x , d.h. verdopple jede Zahl
y =
x , d.h. halbiere jedes Ergebnis wieder
beides Funktionen;
unumkehrbare Funktionen, d.h. die umgekehrte Zuordnung ist nicht mehr eine Funktion (vgl. oben Schüler |→ Schuhgröße).
Den Funktionsgraphen einer (falls vorhanden) Umkehrfunktion kann man durch Spiegelung an der Winkelhalbierenden des 1. Quadranten erhalten. Z.B.
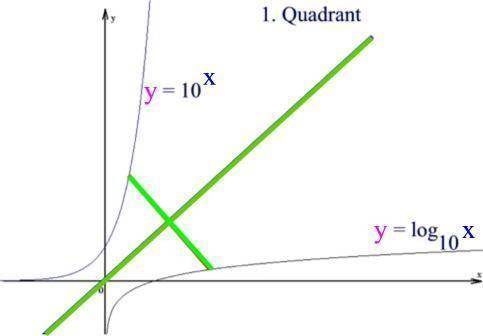
(ebenso y = x2 → y =
oder y = 2x → y =
x )
Ein einzelner Punkt besteht immer aus zwei Koordinaten.
Geometrie Algebra ein Punkt P (a | b) liegt genau dann auf dem Graphen der Funktion f wenn seine Koordinaten (Zahlen!) die Funktionsgleichung von f erfüllen: b = f(a)
Dabei bedeutet "genau dann ... wenn", dass die geometrische und die algebraische Aussage immer gleichzeitig (nicht) gelten.
Beispiele:
- Liegt der Punkt P(2|10) auf dem Graphen der Funktion
f: y = 3 ● x + 4?
Einsetzen der Koordinaten von P in die Funktionsgleichung ergibt 10 = 3 ● 2 + 4, also eine algebraisch richtige Aussage, und damit liegt der Punkt P tatsächlich auf dem Graphen von f.- Liegt der Punkt Q(2|11) auf dem Graphen der Funktion
f: y = 3 ● x + 4?
Einsetzen der Koordinaten von P in die Funktionsgleichung ergibt 11 = 3 ● 2 + 4, also eine algebraisch falsche Aussage, und damit liegt der Punkt P nicht auf dem Graphen von f.
(Nebenbei: da f eine Funktion ist, kann Q gar nicht auf dem Graphen liegen, wenn schon P auf ihm liegt, denn Q liegt über P.)
f : y = f(x) Funktionsname zur Unterscheidung von anderen Funktionen (also z.B. g oder h).
Der Doppelpunkt bedeutet hier nicht "geteilt durch", sondern "definiert als"Funktionsterm
(vgl. oben: die Rechenmaschine, mit der man zu jedem x das zugehörige y errechnet)Funktionsgleichung
Zuordnungsvorschrift: x |→ f(x)
= yDiese ZuordnungsVORSCHRIFT entspricht der einen oben genannten Regel, die unterschiedslos auf sämtliche x angewandt wird. Es ist eine brutale Vorschrift, nach der sich alle x zu richten haben:


Wichtig dabei ist, dass in die Funktion
für x jede Zahl aus dem Definitionsbereich eingesetzt werden kann,
dass aber - wenn man erst mal eine Zahl für x ausgewählt hat - für x (wie immer bei Variablen) immer dieselbe Zahl eingesetzt werden muss.
Ein Beispiel:
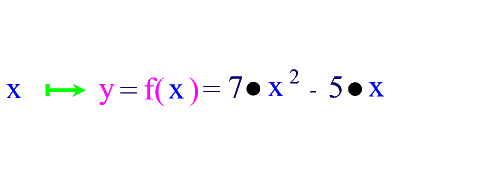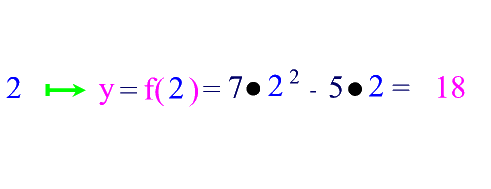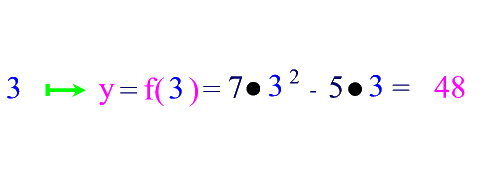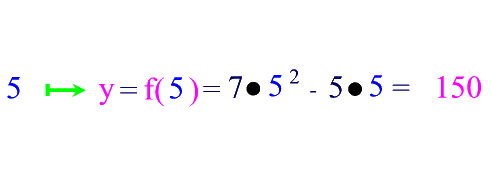
Bei Funktionsgraphen gibt es einige Standardpunkte, die von besonderer Bedeutung sind, weil
- man mit ihnen schnell die Lage der Graphen erfassen und sie somit zeichnen kann,
- sie inhaltlich sehr aussagekräftig sind
(z.B. besagt ein Nullpunkt beim Verlauf von Firmengewinnen, wann die Firma in die Pleite rutscht bzw. wieder aus ihr heraus kommt).

Hier sind A, C und D lokale Maxima (in ihrer Umgebung die höchsten Punkte), während B absolutes Maximum ist (der höchste Punkt des gesamten [auf dem Bild sichtbaren] Gebirges).
(Vgl.
"der größte lebende Mensch" = der größte derzeit lebende Mensch, aber nicht unbedingt der größte Mensch aller Zeiten,
"der größte, lebende Mensch" = der größte Mensch aller Zeiten, der außerdem derzeit lebt.)
Hier sind A, B und C lokale Minima (in ihrer Umgebung die tiefsten Punkte), während D absolutes Minimum ist (der tiefste Punkt des gesamten [auf dem Bild sichtbaren] Gebirges).
Zudem liegt in D ein sogenanntes "Randextremum" vor: es bleibt unklar, ob das Gebirge rechts von D (außerhalb des Bildes)
doch wieder ansteigt (dann wäre D ein Minimum)
gleich hoch bleibt (dann wäre D kein Minimum, sondern ein Knick- oder Sattelpunkt),
weiter abfällt (dann wäre D kein Minimum, sondern nur ein Punkt in einer abfallenden Kurve).
Ein Beispiel ist das Verhalten des Funktionsgraphen von f: y = x3 im Koordinatenursprung:
Da sticht der Graph nicht schräg durch die x-Achse, sondern macht (von links und rechts) eine "weiche" Landung:
MathematikerInnen interessieren sich oftmals weniger für Einzelpunkte (Einzelfälle) als für den Gesamtverlauf eines Graphen (einer ganzen Serie). Denn ein Einzelpunkt besagt reichlich wenig über die Entwicklung und könnte auf unterschiedlichsten Graphen liegen:
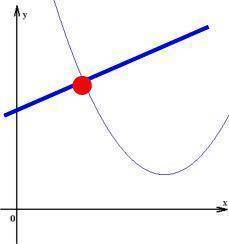
Bzw. Einzelpunkte sind daher oftmals nur insofern von Interesse, wie sie etwas über den Gesamtgraphen aussagen. Solche Aussagen wie "Wende-", "Hoch-", "Berühr-" oder "Sattelpunkt" machen nur im Hinblick auf die Gesamtentwicklung eines Graphen, nicht aber im Hinblick auf einen Einzelpunkt Sinn.
(Vgl.: man kann alleine nicht Bester oder Schlechtester sein.
Einzige Ausnahmen sind da die Schnittpunkte mit den Koordinatenachsen, die auch solche bleiben würden, wenn der ganze sonstige Graph wegfiele.)
Z.B. besagt ein Maximum zwar, dass ein Höhepunkt erreicht ist, aber eben auch, dass es danach wieder bergab geht. Ein Maximum (z.B. von Unternehmensgewinnen) ist also weniger Anlass zur (verfrühten) Freude als vielmehr einer zur Sorge.
(Vgl. "die Hochzeit ist [angeblich] der schönste Tag im Leben einer Frau"; d.h. aber doch, dass es danach nur noch weniger gut, wenn nicht gar schlimmer werden kann.)
- zwar immer Funktionen enthalten,
- mit denen aber teilweise extrem unterschiedlich gerechnet wird,
- die sich graphisch extrem unterschiedlich verhalten
- und die man deshalb niemals verwechseln darf.
Daraus folgt:
Bevor man mit einer Funktion losrechnet oder sie zeichnet, mache man sich grundsätzlich klar, zu welcher Funktionenfamilie sie gehört. (Beispielsweise mache man sich vor jeder Rechnung immer klar, wie viele Nullstellen eine untersuchte Funktion denn überhaupt haben kann - damit man nicht zu viele oder zu wenig berechnet.)
Die Unterschiede zwischen den Funktionenfamilien betreffen erst mal das äußerliche Erscheinungsbild (seine Aussagekraft, aber auch seine Ästhetik)

- steigend oder fallend,
- punkt- oder achsensymmetrisch,
- stetig (mit einem durchgehenden Strich zeichenbar) oder nicht stetig (Lücken),
- differenzierbar (ohne Knicke und Spitzen) oder nicht (überall) differenzierbar
- harmloses Verhalten (z.B. linear wachsend) oder gefährliches Verhalten (z.B. exponentiell explodierend),
- periodisch (s.u. trigonometrische Funktionen),
- asymptotisch gegen andere Linien (Geraden) laufend,
- nach einer Regel (s.o.) oder völlig chaotisch.
Solche Grundeigenschaften sollten auch in Planskizzen immer deutlich werden
(weil man sonst ausgehend von der suggestiven Planskizze auch zu falschen rechnerischen Ergebnissen kommt: man rechnet nur, was man sieht).
Beispielsweise eine Parabel darf also nicht "zackelig" und unsymmetrisch "daherkommen".
Die wichtigsten Funktionenfamilien (jeweils mit besonderen Eigenschaften):
- ganzrationale Funktionen
y = axn + bxn-1 ... + c
(wichtig: das x steht in der Basis!)
Das Aussehen richtet sich weitgehend nach dem höchsten Exponenten.
Insbesondere gibt
- a die Streckung/Stauchung und die Öffnung (nach oben/unten) an
(kann aber auch eine horizontale Verzerrung bewirken),- c den y-Achsenabschnitt
Sy (0 | c).
Spezialfälle:
- höchster Exponent n = 1
y = mx + c
- lineare Funktionen, d.h. der Graph ist eine Gerade; m ist die Steigung und c der y-Achsenabschnitt:
- für m > 0 steigend, für m < 0 fallend
- Spezialfälle (für c = 0) der linearen Funktionen sind die proportionalen Funktionen, die zusätzlich durch den Ursprung gehen.
(Nur) bei proportionalen Funktionen gilt: wenn man den x-Wert vervielfacht, wird der y-Wert genauso vervielfacht
(vgl. wenn man dreimal so viele Bananen kauft, muss man auch dreimal so viel bezahlen)
- höchster Exponent n = 2
y = ax2 + bx + c
- quadratische Funktionen, parabelförmig
Vgl.
- all die parabelförmigen Brücken,
(Nebenbei: es war ein wahrhaft genialer [genial einfacher] Gedanke Roger Angels, die Parabelform von Rotationskörpern und Teleskopspiegeln miteinander zu verbinden:
"Die [...] war der Einfall, sie [die Spiegel] im Inneren rotierender Öfen zu gießen. Der Effekt gleicht der Wirkung, die Sie erzielen, wenn sie die Suppe in einem Topf heftig umrühren. Das verflüssigte Glas schwappt zu den Rändern des Behälters, so daß sich in der Mitte eine Vertiefung bildet. [...] Da das Glas während des Abkühlens seine Rotation beibehält, ist die Parabel auch nach dem Erstarren des Glases noch vorhanden. Durch den Rotations-oder Schleuderguß fällt ein ganzer Abschnitt des Schleifprozesses fort. Angel schätzt, daß er sich dadurch zwei Jahre Arbeit an dem 8,4-MeterSpiegel erspart und 27 Tonnen Glas, die nicht herausgemeißelt werden müssen."
[zitiert nach Michael Lemmonick: Neue Welten im All]Bleibt allerdings die Frage, warum sowohl Spiegel als auch Rotationskörper parabelförmig sind.)
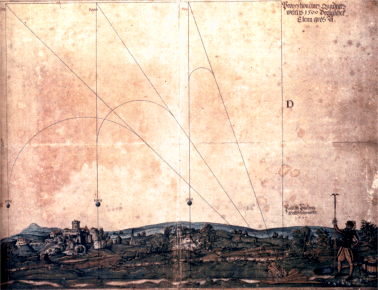
"Kometen haben elliptische Umlaufbahnen. Die Perioden von ungefähr 200 Kometen sind berechnet worden. Eine Periode ist die Zeit, die sie benötigen, um einmal um die Sonne zu kreisen. Sie liegt zwischen 3,3 Jahren für den Encke’schen Kometen und 2 000 Jahren für den Donati’schen Kometen von 1858. Die Umlaufbahnen der meisten Kometen sind so groß, dass sie nicht von Parabeln zu unterscheiden sind. Dies sind offene Kurven, die die Kometen aus dem Sonnensystem hinausführen würden. Aber aus technischen Analysen leiten Astronomen die Annahme ab, dass auch diese großen Umlaufbahnen Ellipsen sind, und zwar sehr exzentrische, deren Umlaufzeiten bis zu 40 000 Jahren oder vielleicht noch viel länger sein können."
(Microsoft Encarta Professional 2002)
- für a = 1 liegt eine Normalparabel vor
- für a > 0 nach oben geöffnet, für a < 0 nach unten geöffnet
- für 0 < |a| < 1 gestaucht
(von oben bzw. unten zusammengedrückt
(da wird die Normalparabel also regelrecht in den Boden gestampft)
- für 1 < |a| gestreckt
(nach oben hoch- oder nach unten runtergezogen:
ein wenig erinnert das an das mittelalterliche Folterinstrument namens Streckbett, in dem die Opfer länger gezogen wurden)(die Koeffizient a vor der höchsten Potenz höhergradiger ganzrationaler Funktionen bewirkt dasselbe!)
- Nullstellenberechnung durch
- quadratische Ergänzung oder
(nach Normierung)- keine, eine oder zwei Nullstellen
- Scheitelpunktsberechnung: quadratische Ergänzung zur Scheitelpunktsform:
y = a (x-d)2+ c
hat den Scheitelpunkt S( d | c)
- Parabeln sind grundsätzlich achsensymmetrisch zu einer Parallelen zur y-Achse, die durch den Scheitelpunkt geht:
- höchster Exponent n = 3
- kubische Funktionen
- s-förmig:
- mindestens eine, höchstens drei Nullstellen
- Nullstellen (in der Schulmathematik) nur berechenbar, wenn mindestens eine bekannt; dann Polynomendivision, um die anderen zu finden
- für a > 0 aus dem Negativen kommend und ins Positive gehend, für a < 0 umgekehrt;
- Spezialfall: rein ungerade Exponenten
punktsymmetrisch zum Ursprung
- die Graphen von Funktionen dritten Grades sind grundsätzlich punkt- bzw. drehsymmetrisch zu ihrem Wendepunkt:
- höchster Exponent n = 4
(honi soit qui mal y pense)
(man könnte auch der Anschaulichkeit halber sagen: eine Pobacke hängt neben dem Hocker runter)
- Nullstellenzahl: 0;1;2;3;4
- Spezialfall: nur gerade Exponenten/biquadratisch:
- achsensymmetrisch zur y-Achse
- Nullstellen (soweit vorhanden) durch Substitution z = x2 ermittelbar
- höchster Exponent n gerade
- im Prinzip parabelförmig (s.o.), evtl. mit Schlenkern in der Mitte
(solche Funktionen gehören fast ins Kuriositätenkabinett eines mittelalterlichen Jahrmarkts: sie haben mehr als zwei "Pobacken";
es gibt auch Funktionen ohne "Po-Ritze", nämlich z.B. die einfachsten:
)
- evtl. keine Nullstelle, höchstens n Nullstellen
- höchster Exponent n ungerade
- im Prinzip s-förmig (s.o.) mit Schlenkern in der Mitte
- mindestens eine, höchtens n Nullstellen
- Wurzelfunktion
y =
(wichtig: das x steht unter der Wurzel)
(nach rechts geöffnete Parabel, nur oberer Ast)
- Hyperbelfunktion
y =
"Sie berühren sich [an allen Koordinatenachsen] im Unendlichen!" - "Wie romantisch!"
bzw. sie berühren sich eben gerade niemals
(wichtig: das x steht im Nenner)
- asymptotisch gegen die x- und y-Achse laufend:
"»Ach«, sagte die Maus, »die Welt wird enger mit jedem Tag. Zuerst war sie so breit, daß ich Angst hatte, ich lief weiter und war glücklich, daß ich endlich rechts und links in der Ferne Mauern sah, aber diese langen Mauern eilen so schnell aufeinander zu, daß ich schon im letzten Zimmer bin, und dort im Winkel steht die Falle, in die ich laufe.« – »Du mußt nur die Laufrichtung ändern«, sagte die Katze und fraß sie." (Franz Kafka)
- Exponentialfunktionen
(Wachstum der Erdbevölkerung;
Modell im Deutschen Museum, München)y = b ● ax
(wichtig: das x steht im Exponenten)
auch hier gilt wieder: "Sie berühren sich [links] im Unendlichen!" - "Wie romantisch!"
bzw. sie berühren sich eben gerade niemals
- nur für a > 0 definiert!
- für 0 < a < 1 fallend
(dann asymptotisch gegen die positive x-Achse)- für 1 < a steigend
(dann asymptotisch gegen die negative x-Achse)- keine Nullstelle!
- wenn man ein beliebiges x um 1 erhöht, wird das zugehörige y ver-a-facht
- b ver-b-facht jeden y-Wert, d.h. staucht oder streckt den Graphen
(nicht zu verwechseln mit einer Verschiebung nach oben oder unten)- viele natürliche und naturwissenschaftliche Prozesse verhalten sich exponentiell, d.h. sie sehen anfangs trügerisch harmlos, nämlich fast linear aus - und explodieren dann rasant und immer schneller (werden aber nie senkrecht, weil dann gar keine Funktionen mehr vorliegen würden)
- Exponentialfunktionen steigen für große x erheblich rasanter als sämtliche Potenzfunktionen (z.B. auch x1000).
- Logarithmusfunktionen
y = logb x
- eine Nullstelle
- nur für x > 0 definiert, deshalb keine Werte links der y-Achse
- asymptotisch gegen die negative y-Achse
- als Umkehrfunktion der Exponentialfunktion steigt die Logarithmusfunktion für große x erheblich langsamer als sämtliche Potenzfunktionen (und wird dennoch rechts nie parallel zur x-Achse, also nie konstant).
- trigonometrische Funktionen
- sind alle periodisch
- haben deshalb alle auch unendlich viele Nullstellen
- Sinusfunktion
Axe-Reklame: "Ach wie nett, du hast meinen Busen bemerkt."
(lat. sinus = Bucht, Busen; vgl.
)
- Cosinusfunktion
(die Sinus- und die Cosinusfunktion haben die Besonderheit, dass sie nach oben und unten beschränkt sind, also nie aus dem "Käfig" zwischen -1 und 1 heraus können:
auf die Gefahr hin, fälschlich in den Verdacht zu geraten, sexistisch zu denken oder dem Jugendkult anzuhängen: so wie Parabeln schön geschwungen aussehen sollten, müssen auch Sinus- und Cosinusgraphen harmonisch fließen wie der Busen eines "knackigen" jungen Mädchens - und nicht wie der einer alten Frau:
es liegt nicht an mir, dass "Sinus" nun mal "Busen" bedeutet, und Männer, die nur nach solchen [schönen!] äußerlichkeiten gehen, sollten vor allem mal an sich selbst herab sehen;
vgl. auch)
- Tangensfunktion
an einigen Stellen nicht definiert; in deren Nähe jeweils asymptotisch gegen Parallelen zur y-Achse laufend
(anders als bei kubischen Funktionen!)- Cotangensfunktion
an einigen Stellen nicht definiert; in deren Nähe jeweils asymptotisch gegen Parallelen zur y-Achse laufend
| "The Great Curve [...] The world moves on a womans hips The world moves and it swivels and bops The world moves on a womans hips The world moves and it bounces and hops [...]" (Talking heads) |
Wie schon oben gesagt, beschäftigen sich MathematikerInnen ungern mit Einzelfällen, sondern suchen sie immer nach möglichst allgemeine Gesetzen, also z.B.
- nicht die Winkelsumme in einem Dreieck, sondern die in allen Dreiecken
(in der Ebene immer 1800;
vgl.)
- nicht die Beziehung zwischen den drei Seiten in einem bestimmten rechtwinkligen Dreieck, sondern die in allen rechtwinkligen Dreiecken
(Satz des Pythagoras a2 + b2 = c2) .Mathematiker versuchen immer, "möglichst viele [am besten alle] Fliegen mit einer Klappe zu erschlagen".
(Es ist allemal bemerkenswert, dass die Mathematik als einzige Wissenschaft Aussagen für alle / unendlich viele Fälle machen kann - und dass die Beweise paradoxerweise oftmals dennoch sehr kurz sind.)
Meistens läuft das so, dass
- den MathematikerInneN nach der Behandlung einiger konkreter Beispiele eine (noch allgemein zu beweisende, weil eventuell nur scheinbare!) Gemeinsamkeit auffällt bzw.
- sie nach dem zweiten oder dritten Beispiel keine Lust mehr haben und deshalb nach einer allgemeinen Regel suchen.
(Man stellt mit Vorliebe dann eine Regel auf, wenn sie auf die Dauer mehr Mühe erspart, als sie anfangs bereitet. Allerdings "lieben" MathematikerInnen in ihrem Bemühen um Ordnung Regeln auch um ihrer selbst willen und staunen immer wieder, wo überall Regeln auffindbar sind.)
Z.B. stellen MathematikerInnen irgendwann fest:
- der Graph von y = 1 ● x2 ist parabelförmig,
- der Graph von y = 2 ● x2 ist parabelförmig,
- der Graph von y = 3 ● x2 ist parabelförmig
- ... also wird auch der Graph von y = a ● x2 parabelförmig sein
(wir wissen ja inzwischen, dass das a die Parabel nur streckt oder staucht, wodurch aber immer wieder eine Parabel entsteht).Also betrachten MathematikerInnen in ihrem Verallgemeinerungswahn ab sofort nicht mehr Einzelparabeln, sondern alle Parabeln mit Gleichungen der Form y = a ● x2.
Hinter der unscheinbaren Gleichung y = a ● x2 steckt also eine "Funktionenschar" aus unendlich vielen Parabeln
(wenn einem der geometrische Aspekt wichtiger ist, spricht man auch von "Kurvenscharen"):
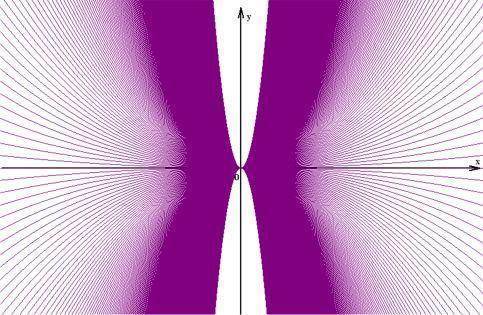
(hier sind nur einige Parabeln für -10 < a < 10 mit Zwischenschritten von 0,1 eingezeichnet, weshalb noch seitlich schmale Streifen und oben und unten große Flächen leer bleiben)
Wenn man alle Graphen zur Gleichung y = a ● x2 einzeichnen würde, so würde das gesamte Koordinatensystem violett eingefärbt (außer der dann allerdings kaum mehr erkennbaren y-Achse).
Ein besonders schöner Effekt ergibt sich aber, wenn die einzelnen Funktionsgraphen einer Funktionenschar nacheinander erscheinen:
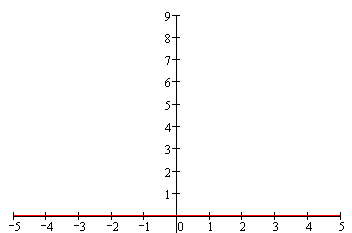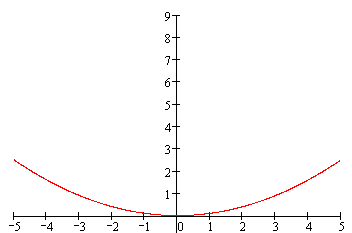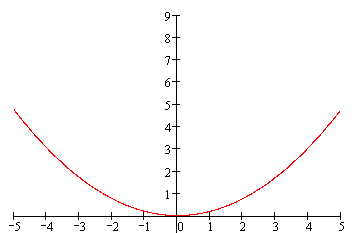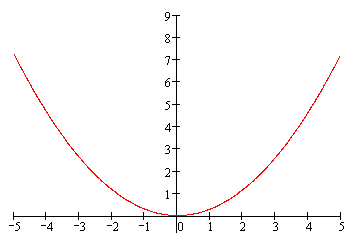
Das sieht dann so ähnlich aus wie eine sich öffnende oder schließende Blume:
Im Gegensatz zur (freien) Variablen x und der (abhängigen) Variablen y nennt man a auch "Formvariable".
Eine weitere Funktionenschar wäre z.B. y = a ● x3 :
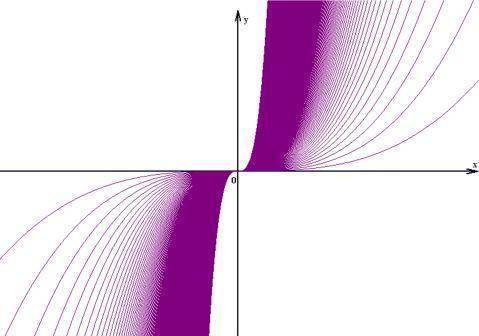
(hier sind nur einige Funktionsgraphen für 0 < a < 10 mit Zwischenschritten von 0,1 eingezeichnet, weshalb noch große Flächen leer bleiben)
Wenn man auch hier wieder alle Graphen zur Gleichung y = a ● x3 einzeichnen würde, so würde ebenfalls das gesamte Koordinatensystem violett eingefärbt (außer der dann allerdings kaum mehr erkennbaren x- und der y-Achse).
Will man nun aus der Funktionenschar y = a ● x3 eine spezielle Einzelfunktion haben, so
wählt man als erstes (!!!) einen anfangs beliebigen konkreten Wert für die Formvariable a, also z.B. a = 4,
und erhält dann (nach endgültiger Festlegung des a) die konkrete Einzelfunktion y = 4 ● x3 , bei der wohlgemerkt x noch immer völlig frei wählbar ist, woraus sich dann das jeweils zugehörige y berechnen lässt.
Solche Funktionenscharen lassen sich dann auf übergreifende Gemeinsamkeiten hin untersuchen. Z.B. liegen - wie sich beweisen lässt - alle Minima der Funktionenschar y = a x3 - x2 auf der Parabel y = -
x2 :
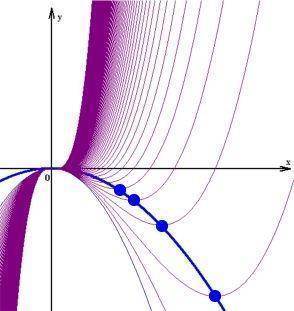
Und das ist doch allemal staunenswert:
woher "wussten" die Minima der verschiedenen Einzelgraphen voneinander?
warum liegen die Minima von Funktionen dritten Grades auf einer erheblich einfacheren, nämlich quadratisch-parabelförmigen Kurve?
bzw. warum liegen die Minima überhaupt so hübsch regelmäßig?
An Funktionenscharen wird besser als an Einzelfunktionen deutlich, was an den jeweiligen Funktionenfamilien (s.o.) besonders auffällig ist bzw. was alle Mitglieder einer jeweiligen Familie gemeinsam haben und welche Eigenschaften solch eine Familie überhaupt ausmachen.
Zudem erinnert die Betrachtung von Funktionenscharen ans mathematische Fachgebiet der Topologie:

"Topologie, Zweig der Mathematik, in dem bestimmte Eigenschaften geometrischer Figuren untersucht werden. Das Wort Topologie wurde 1930 von dem Mathematiker Salomon Lefschetz geprägt. Gewöhnlich wird Topologie der Geometrie zugeordnet; sie befasst sich mit denjenigen Eigenschaften geometrischer Figuren im Raum, die sich nicht verändern, wenn der Raum in irgendeiner Art gekrümmt, verdreht, gedehnt oder verformt wird [...]. Die Geometrie beschäftigt sich mit Eigenschaften wie der absoluten Position [...], die Topologie dagegen nur mit Eigenschaften [...] wie der relativen Position und der allgemeinen Form."
(Microsoft Encarta Professional 2002)Wie kann ich einen Funktionsgraphen verbiegen, ohne die Besonderheiten seiner Familie zu verlieren?
Funktionenscharen "in freier Wildbahn":
Bemerkenswerter als die Unterschiede zwischen den drei Ausflüssen scheint mir jeder Einzelausfluss, bei dem das auslaufende Wasser jeweils eine Funktionenschar (von Parabeln) bildet.
die (Parabel-)Funktionenschar, die sich bei jedem Viereck(rasen)regner
bildet, wenn er hin und her schwenkt.