Fleisch an die Knochen der Funktionsgleichungen

(wobei Funktionsgraphen 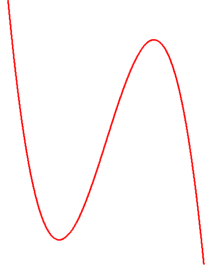allerdings auch noch nicht gerade sexy sind)

Funktionen (ohne Zusatz) sind arg abstrakte Sachen, die nur auf zweierlei Weisen "sichtbar" werden:

• als Funktionsgraphen,
• als Funktionsgleichungen.

Nun sind aber Funktionsgleichungen

(zumindest auf den ersten Blick)

• reine Texte aus Zahlen, Einzelbuchstaben und Vor-/Rechenzeichen,
• also kryptische Ansammlungen von Druckerschwärze, nämlich z.B.

y = x² - 3 - x³ + x .

Eine zentrale Tätigkeit in der Oberstufen-Mathematik ist daher die "Kurvendiskussion":

• anfangs ist immer eine Funktionsgleichung gegeben, also

(so könnte man bösartig sagen)

etwas möglichst Unverständliches;

• durch eine Reihe von Rechnungen sollen dann Einzelheiten des Funktionsgraphen herausgefunden werden wie z.B. Nullstellen, Extrem - und Wendepunkte

(also allesamt Einzelpunkte);

• wenn's hoch kommt, werden die soeben genannten Einzelheiten dann zu einem Funktionsgraphen zusammengesetzt.

Freundlicher gesagt: Sinn der "Kurvendiskussion" ist es,

• aus etwas Abstraktem (einer Funktionsgleichung)
• etwas Anschauliches (einen Funktionsgraphen)

zu machen

(was überhaupt erst mit dem Koordinatensystem möglich ist).

Die vorgebliche "Kurvendiskussion" ist also in Wirklichkeit eher eine Kurvenherstellung

(... was man durchaus wörtlich nehmen kann: wir nageln wichtige Punkte auf ein Brett und legen eine

Rohrreinigungsspirale

um die Nägel herum; s.u.).

Im Zeitalter der Computer bzw. "Grafikfähigen Taschenrechner [GTR]" könnte man sich den ganzen Aufwand sparen, weil sie nach Eingabe der Funktionsgleichung sofort den fertigen Funktionsgraphen anzeigen

(und auf Wunsch auch Zahlenwerte für o.g. "Einzelheiten").

Die Anhänger der "Computer-Mathematik-Didaktik"

(was ich hier mal fesch als "CoMaDi" abkürze)

weisen zwar immer wieder darauf hin, dass die Schüler auch noch die "manuelle" Kurvendiskussion beherrschen müssen, erhoffen sich vom Computereinsatz aber vor allem doch die Befreiung vom stumpfen Rechnen und damit Zeit für tieferes bzw. überhaupt erst Verständnis.

Ich glaube aber, dass dieses Verständnis auch viel preiswerter zu haben ist.

Zurück zu

"aus etwas Abstraktem (einer Funktionsgleichung) etwas Anschauliches (einen Funktionsgraphen) [...] machen":

ein Funktionsgraph besteht aus unendlich vielen Punkten, weshalb es doch schön wäre, ihn aus möglichst wenigen Einzelheiten zusammensetzen zu können:

1. einem Wissen über seine grundsätzliche Form,
2. einigen wenigen markanten und gleichzeitig hoffentlich möglichst einfach zu berechnenden Punkten,
3. den Verbindungslinien zwischen diesen markanten Punkten, so dass man dann doch noch die unendlich vielen Punkte erhält.

Vorgeführt sei all das anhand der schon oben genannten Funktionsgleichung

y = x² - 3 - x³ + x .

Zu 1., also dem Wissen über die grundsätzliche Form eines Funktionsgraphen:

die wichtigste Eigenschaft einer Funktionsgleichung

(genau genommen der Gleichung einer "ganzrationalen" Funktion)

ist ihr höchster Exponent, im vorliegenden Fall also

y = x² - 3 - x³ + x .

(Weil der höchste Eponent 3 weitgehend das Aussehen des Funktionsgraphen bestimmt, nennt man f auch eine "Funktion dritten Grades".)

Wenn einem also in freier Wildbahn eine schwerverletzte Funktionsgleichung begegnet und sie mit letzter Kraft "diskutiere mich!" haucht, "scanne" man sie zu allererst nach dem höchsten Exponenten ab:

.

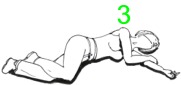Lehrer sind gerne gemein, und deshalb habe ich in y = x² - 3 - x³ + x den höchsten Exponenten 3 irgendwo in der Mitte versteckt. Üblicherweise sind aber die Einzelterme einer Funktionsgleichung schön nach der Größe der Exponenten geordnet, und deshalb hole man das mal schnell nach:

y = - x³ + x² + x - 3 .

Die grundsätzliche Form des Funktionsgraphen entscheidet sich also ganz vorne bei - x³ , und der ganze restliche Rattenschwanz + x² + x - 3 ändert daran nur noch wenig,

• fügt nämlich höchstens noch einige "Schlenker" hinzu und
• ändert eventuell die Lage des Funktionsgraphen.

Aus dem höchsten Exponenten 3 folgt, dass der Funktionsgraph "s-förmig" ist, also ungefähr so aussieht:

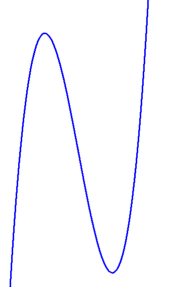
Dabei übersieht man allzu gerne den einfachsten Fall ohne Schlenker nach oben und unten, der beispielsweise bei der nackten Funktion f: y = x³ vorliegt:

 Unbedingt noch zu beachten ist, dass

• eine Funktion vorliegt,
• jedem x also genau ein y zugeordnet wird,
• beim Funktionsgraph also nicht mehrere Punkte übereinander liegen dürfen und somit
• der Funktionsgraph nie
• senkrecht werden oder
• rückläufig sein darf:

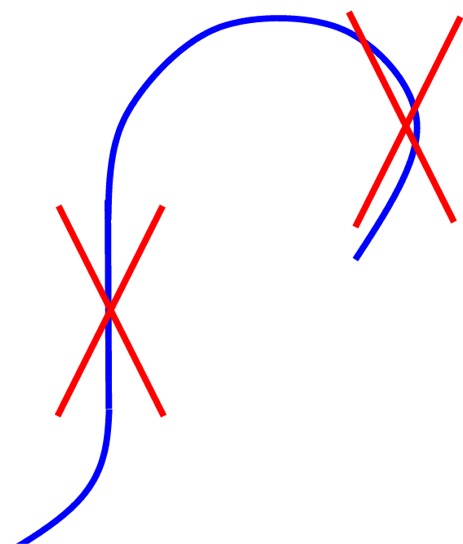
(Korrekte Funktionsgraphen sind gar nicht so leicht freihand zu zeichnen, da sie an den Seiten sehr steil werden, aber nie senkrecht werden dürfen. Glücklicherweise sind die in der Schule üblichen Funktionsgraphen aber um den Ursprung herum, wo sich alles Wichtige abspielt, noch nicht ganz so steil.)

Im Term - x³ mit dem höchsten Exponenten entscheidet sich nun noch mehr:

1. sorgt das Minus im Vergleich mit dem Standardgraphen für eine Spiegelung an der x-Achse, so dass der Funktionsgraph

• nicht mehr von unten kommt und nach oben geht, sondern

• umgekehrt von oben kommt und nach unten geht:

(Preisfrage:
wo läge hier die x-Achse?)

2. sorgt der Koeffizient für eine Stauchung des bisherigen Funktionsgraphen, der somit insgesamt flacher wird:

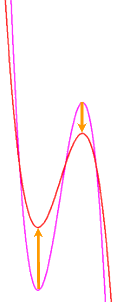
(Preisfrage:
wo läge hier die x-Achse?)

Es sei nochmals betont, dass wir aus dem Term - x³ mit dem höchsten Exponenten 3

• "nur" die ungefähre Form des Funktionsgraphen, aber
• noch nicht seine Lage ablesen konnten

(weshalb bislang auch noch kein Koordinatensystem gezeichnet wurde).

Zu 2., also einigen wenigen markanten und gleichzeitig hoffentlich möglichst einfach zu berechnenden
           Punkten:

als besonders markante Punkte sämtlicher Funktionen gelten zurecht

(soweit vorhanden)

• die Nullstellen N , d.h. die Schnittpunkte mit der x-Achse,
• der Schnittpunkt S_y mit der y-Achse,
• die Extrempunkte (Minima bzw. Maxima),
• die Wendepunkte.

Glücklicherweise sind all diese Punkte auch halbwegs einfach (?) zu berechnen:

1. ist bei Nullstellen y = 0 , also die Gleichung 0 = - x³ + x² + x - 3 zu lösen,
2. ist beim Schnittpunkt S_y mit der y-Achse x = 0,
3. muss bei Extrempunkten die

(hier nicht näher erklärte)

erste "Ableitung" gleich 0 sein

(und noch eine weitere Bedingung erfüllt sein),

4. muss bei Wendepunkten die

(hier ebenfalls nicht näher erklärte)

zweite Ableitung gleich 0 sein

(und ebenfalls noch eine weitere Bedingung erfüllt sein).

Alles läuft also darauf hinaus, Gleichungen mit Nullen zu lösen, was vor allem mit der

(unbedingt zu beherrschenden!)

pq-Formel 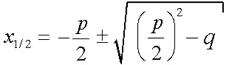möglich ist.

Ein besonders schöner, weil einfacher Fall ist b., also die Berechnung des Schnittpunkts S_y mit der y-Achse. Wie gesagt, ist da x = 0 , weshalb wir nun 0 für sämtliche x in der Funktionsgleichung

                                           y = -   x³ + x² +   x - 3

einsetzen und dann

                                           y = - •0³ + 0² + •0 - 3

                                           y =        0   + 0    + . 0 - 3

                                   y =                                -3

erhalten. Wenn wir derart erstmal verstanden haben, dass

• alle Terme, in denen x vorkommt, Null werden und
• nur der letzte Term hinten, in dem kein x vorkommt, übrig bleibt,

können wir uns ab sofort das Rechnen sparen und den y-Wert von S_y auch einfach nur hinten ablesen.

(Den letzten Term hinten, in dem kein x vorkommt und an dem somit auch kein x irgendwas verändern kann, nennt man deshalb auch "absolutes Glied".)

Es ergibt sich also S_y ( 0 | -3 ):

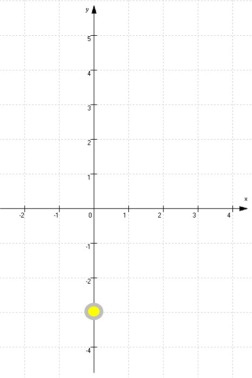
Schon oben war im Singular von DEM Schnittpunkt S_y mit der y-Achse die Rede, denn es kann

(im Gegensatz zu den Schnittpunkten mit der x-Achse, also den Nullstellen)

bei sämtlichen Funktionen und Funktionsarten nie MEHRERE Schnittpunkte S_y mit der y-Achse geben, da diese ja übereinander lägen und somit keine Funktion mehr vorläge

(da ganzrationale Funktionen aber stetig, also "durchgehend" sind, haben sie auch tatsächlich [genau] einen Schnittpunkt S_y mit der y-Achse, denn auf ihrem Weg von links nach rechts müssen sie irgendwo die y-Achse durchqueren:

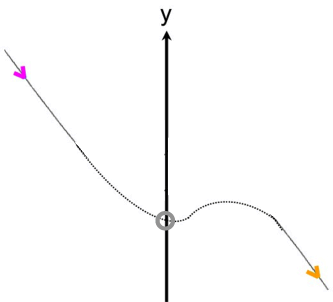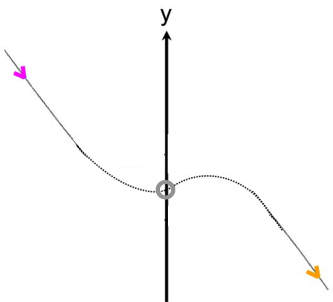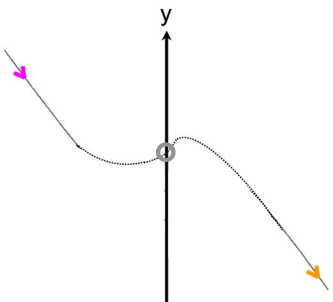
[vgl. sogenannte Feynman-Pfadintegrale wie z.B. ];

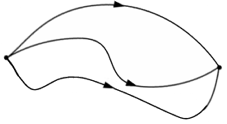es ist also nicht möglich, dass ganzrationale Funktionen keinen Schnittpunkt S_y mit der y-Achse haben;

für einige Verwirrung sorgt es bei Schülern gerne, wenn in der Funktionsgleichung [scheinbar] gar kein "absolutes Glied" auftaucht wie beispielsweise in y = x³ . "Gar kein absolutes Glied" ist aber gleichbedeutend mit dem absoluten Glied Null, so dass sich die Funktionsgleichung y = x³ + 0 ergibt, wo man am Ende dann eben doch den y-Achsenabschnitt 0 ablesen kann und somit S_y ( 0 | 0 ) ist;

•  sowohl ihren Schnittpunkt S_y mit der y-Achse

• als auch einen Schnittpunkt mit der x-Achse, also eine Nullstelle:

).

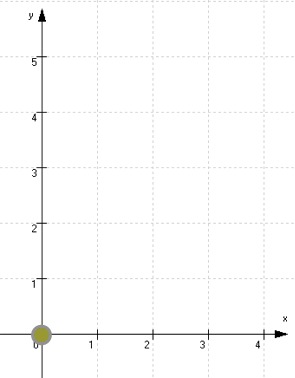Mit S_y ( 0 | -3 ) haben wir nun aber einen ersten Punkt des Funktionsgraphen und somit auch eine erste Information zu seiner Lage:

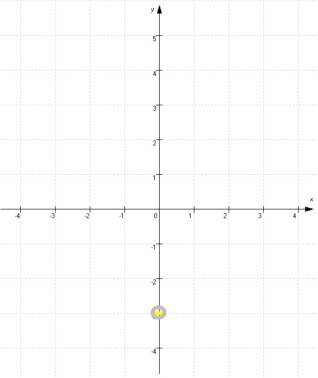
Allerdings können durch diesen Punkt unendlich viele Funktionsgraphen gehen, nämlich z.B.

,

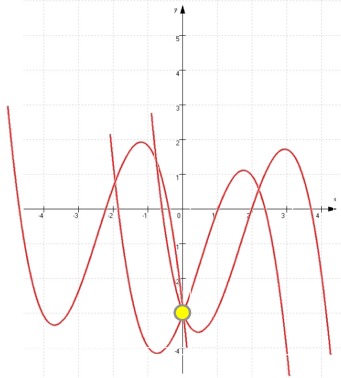weshalb wir noch ein paar andere Punkte (Nullstellen, Extrem- und Wendepunkte ) brauchen.

Wie sparen uns aber deren Berechnung (mittels der "Ableitungen"), weil Verständnis viel wichtiger ist

(kommt hinzu, dass es gar nicht so einfach ist, die Nullstellen von Funktionen dritten Grades zu berechnen; bzw. sie lassen sich in der Schule eh nur berechnen, wenn sie einfach sind;

dazu braucht man allerdings die bei Schülern so unbeliebte und dennoch grandiose Polynomendivision).

1. Funktionsgraphen dritten Grades haben

(anders z.B. als einige Funktionen zweiten Grades [Parabeln])

 immer mindestens eine Nullstelle, da die Funktionsgraphen

• "stetig", also ununterbrochen sind,

• von unten kommen und nach oben gehen (oder umgekehrt) und deshalb

• irgendwo auf dem Weg von unten nach oben (oder umgekehrt) die x-Achse durchstoßen müssen:

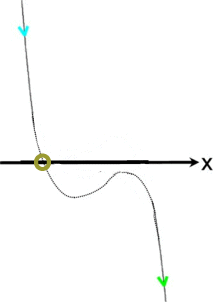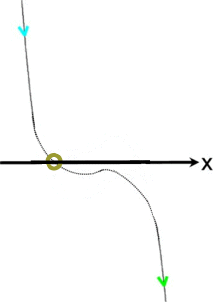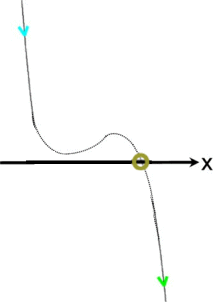
Funktionsgraphen dritten Grades können

• eine, zwei oder drei Nullstellen haben

,

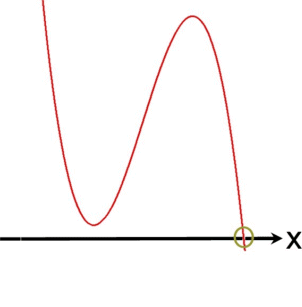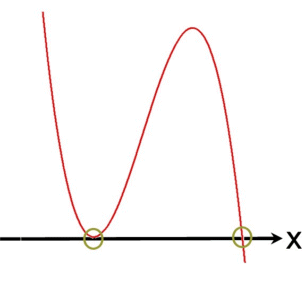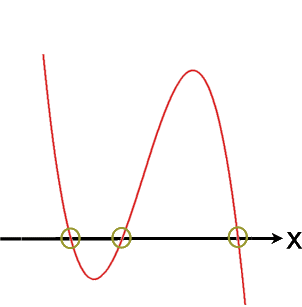• aber nicht noch mehr (vier, fünf ...).

2. Funktionsgraphen dritten Grades haben immer genau einen Wendepunkt

(an dem eine Links- in eine Rechtskurve übergeht oder umgekehrt);

dieser Wendepunkt entspricht der Nabe eines Propellers:

(b. wird hier - genauso wie c., d. und e. im Folgenden - nicht bewiesen);

Wenn eine Funktion nur (genau) einen Wendepunkt hat, folgt daraus, was oben nur ohne Begründung festgestellt wurde, nämlich, dass sie dann s-förmig ist, d.h. links vom Wendepunkt eine Rechts- und rechts vom Wendepunkt eine Linkskurve (oder umgekehrt).

(Durchaus interessant ist aber auch der Beweis, dass jede [!]  Funktion dritten Grades genau einen Wendepunkt hat. Dazu werden wir zwischendurch mal kurz unanschaulich:

• Funktionsgleichungen dritten Grades sehen immer so aus: f: y = ax³ + bx² + cx + d, wobei a ≠ 0 sein muss, da sonst keine Funktion dritten Grades vorläge, während b, c und d durchaus gleich Null sein dürfen.

• Leitet man die Funktion einmal ab, so ergibt sich f ': y = 3ax² + 2bx + c.

• Als zweite Ableitung ergibt sich f '': y = 6ax + 2b, und das ist - um wieder halbwegs anschaulich zu werden - eine Geradengleichung. Weil aber a ≠ 0 ist, hat die zugehörige Gerade eine echte Steigung von 6a ≠ 0 und damit (unabhängig von b und sowieso von c und d) genau eine Nullstelle.

• Nun ist es aber eine notwendige Bedingung für einen Wendepunkt, dass die zweite Ableitung gleich Null ist, und das geschieht, wie eben gezeigt, offensichtlich genau einmal.

Faszinierend an diesem Beweis finde ich, dass man von der Funktion nur ganz allgemein wissen muss, dass a ≠ 0  ist.)

3. Funktionen dritten Grades sind immer punktsymmetrisch zu diesem Wendepunkt.

4. Funktionsgraphen dritten Grades haben

• nicht immer Extrempunkte

(z.B. hat f: y = x³ keinen Extrempunkt: )

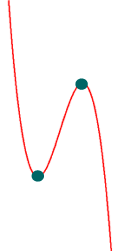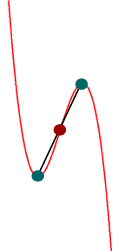
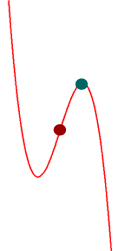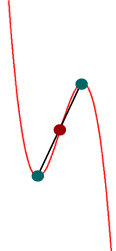
• oder aber genau ein Minimum UND ein Maximum, was sofort aus der Punktsymmetrie zum Wendepunkt folgt.

Aus b. bis d. folgt:

bei Funktionen dritten Grades liegt der Wendepunkt immer genau in der Mitte zwischen (falls vorhanden) dem Minimum und dem Maximum, woraus wiederum folgt:

• wenn man (falls vorhanden) das Maximum und das Minimum hat, braucht man den Wendepunkt gar nicht mehr großartig über die zweite (und dritte) Ableitung zu berechnen:

• wenn man ein Maximum (oder Minimum) sowie den Wendepunkt hat, braucht man das Minimum (oder Maximum) gar nicht mehr großartig über die erste (und zweite) Ableitung zu berechnen, sondern liegt es einfach "auf der anderen Seite" des Wendepunkts :

Jetzt, wo die wichtigsten Eigenschaften der Funktion f: y = - x³ + x² + x - 3 verstanden sind, holen wir uns "irgendwoher" die rechnerischen Ergebnisse für die Nullstellen, Extrempunkte und den Wendepunkt und erhalten

(teilweise gerundete Werte, da man sowieso nicht genauer zeichnen kann):

• N ₁ ( -2 | 0 ), N ₂ ( 1 | 0 ) und N ₃ ( 4 | 0 ),
• Max ( -0,8 | -4,1 ), Min ( 2,1 | 2 ),
• WP ( 0,7 | -1 ).
  

Mit dem bereits oben herausgefundenen Punkt S_y ( 0 | -3 ) haben wir dann die Punkte

.

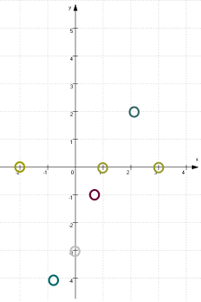Wenn man nun daran denkt, dass jeder Funktionsgraph von links nach rechts durch die vorgegebenen Punkte gehen muss; und wenn man sich des weiteren daran erinnert (s.o.), dass der gesuchte Funktionsgraph ungefähr so

,

aussieht, ahnt man vielleicht schon das genaue Aussehen des Funktionsgraphen.

Wir gehen's hier - wie oben schon angekündigt - erstmal handwerklich an und schlagen für die Punkte Nägel in ein Brett:

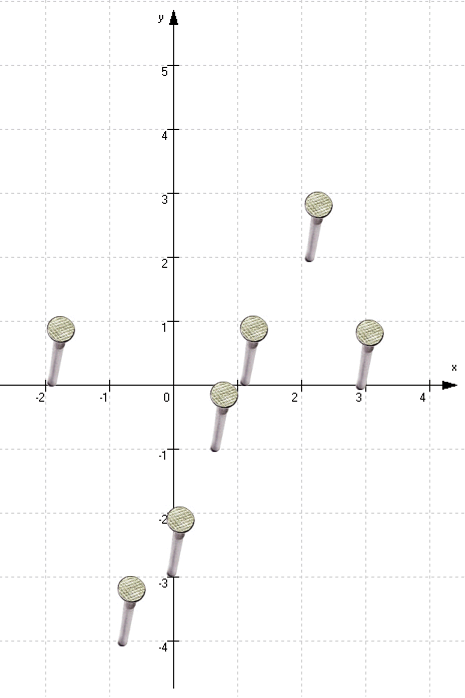
Um diese Punkte legen wir nun eine

Rohrreinigungsspirale

und erhalten damit:

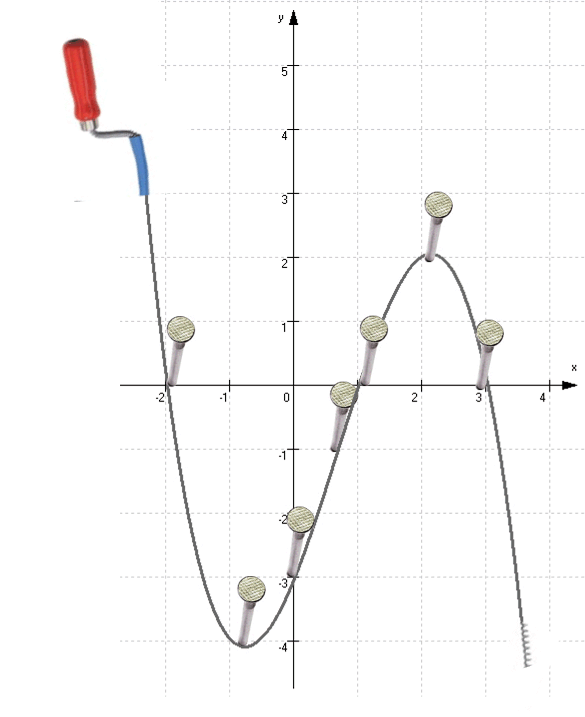
Die Spirale biegt sich dabei automatisch "rundlich", nimmt uns also die Mühen ab, selbst einen "rundlichen" Funktionsgraphen zu finden.

Hier sei aber auch vorgemacht, wie man das am der Tafel oder im Heft macht:

Funktionsgraphen ganzrationaler Funktionen sind überall "differenzierbar", was vereinfacht gesagt heißt, dass sie

• keine Spitzen haben wie z.B. in

,

• sondern überall schön "rundlich" sind.

Um dies insbesondere im Minimum und Maximum zu erreichen, zeichnen wir uns da dünn kleine Halbkreise rein

(wobei der Funktionsgraph sich im Minimum und Maximum nicht exakt, sondern nur ungefähr halbkreisförmig verhält):

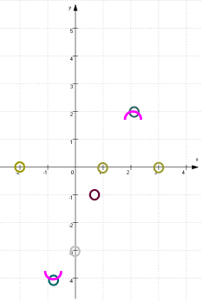
Wir wissen außerdem, dass der Funktionsgraph von links oben kommt und nach rechts unten geht :

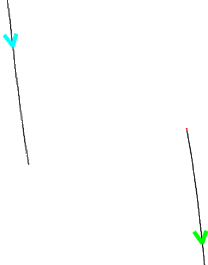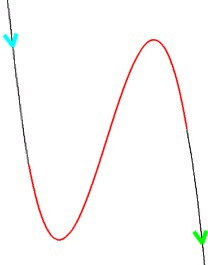
Diese beiden "Äste" des Funktionsgraphen schieben wir nun von links und rechts an die äußeren Nullstellen heran:

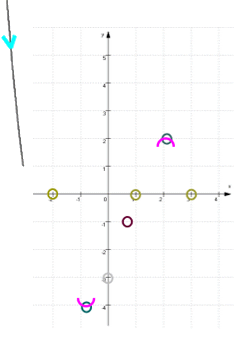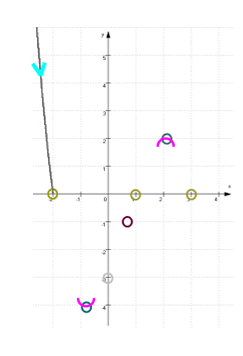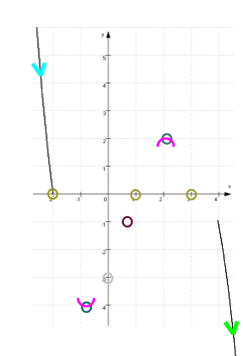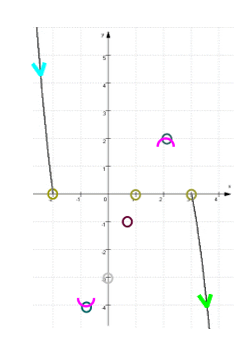
und erhalten dann

.

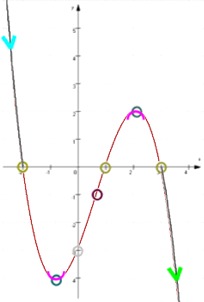Nun sollten Funktionsgraphen ja sowieso grundsätzlich mit angespitztem Bleistift gezeichnet werden, aber bis hier ist es sogar ratsam, nur hauchdünne Linien zu zeichnen und den Bleistift nicht stark aufzudrücken, damit man noch Falsches oder Ungenaues nacharbeiten und leicht ausradieren kann. Erst wenn man einen schön gerundeten Funktionsgraphen hat, trage man "dick auf".

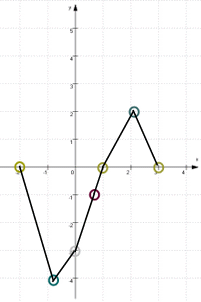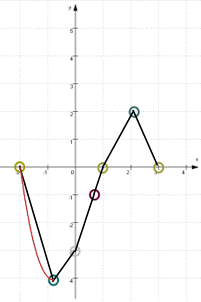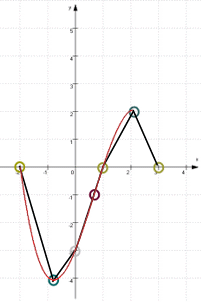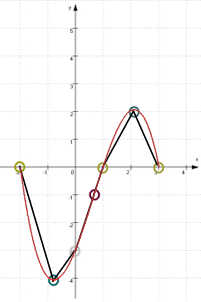
Noch ein kleiner Tipp: wenn man Funktionsgraphen nicht schön rundlich hinkriegt, verbinde man bekannte Punkte erstmal dünn mit Strecken:

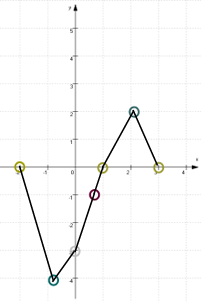
Dann sieht man besser, wo die rundlichen Linien liegen müssten, und kann sie dann ja nachzeichnen:

PS:

Funktionsgraphen geraden Grades (also mit dem höchsten Exponenten 2, 4, 6 ...) sehen im Prinzip alle so aus: bei positivem Term mit dem höchsten Exponenten:          (d.h. der Graph kommt links aus dem Positiven [von oben] und geht rechts ins Positive [nach oben]), bei negativem Term mit dem höchsten Exponenten: (d.h. der Graph kommt links aus dem Negativen [von unten] und geht rechts ins Negative [nach unten]). Funktionsgraphen ungeraden Grades (also mit dem höchsten Exponenten 1, 3, 5 ...) sehen im Prinzip alle so aus: bei positivem Term mit dem höchsten Exponenten:         (d.h. der Graph kommt links aus dem Negativen [von unten] und geht rechts ins Positive [nach oben]), bei negativem Term mit dem höchsten Exponenten: (d.h. der Graph kommt links aus dem Positiven [von oben] und geht rechts ins Negative) [nach unten]). Allerdings sind alle Graphen von Funktionen mit einem Grad von größer oder gleich 2 außen immer "rundlich" nach oben bzw. unten gebogen. Und Funktionen mit einem Grad von größer oder gleich 3 können in der Mitte "Schlenker" haben.  Z.B. der Graph einer Funktion 7. Grades: Ganzrationale Funktionsgraphen können maximal so viele Nullstellen haben, wie ihr Grad ist, ein Funktionsgraph siebten Grades also höchstens 7 Nullstellen:

PPS:	Funktionsgraphen zweiten Grades (Parabeln) wie z.B. der von f: y = x2  sind immer achsensymmetrisch zu einer senkrechten Gerade durch ihren Extrempunkt ; Funktionsgraphen vierten, fünften und höheren Grades können achsen- bzw. punktsymmetrisch sein: ,... ,   sind es aber keineswegs immer: , ...