die "geilste" Funktion aller Zeiten

"geil" sei hier durchaus im doppelten Wortsinne angewandt:

1. vielleicht ein wenig anbiedernd:

geil (Jugendspr. auch für großartig, toll)

2. im ursprünglichen, "schärferen" Sinn:

geil, Das Wort stammt von dem mittelhochdeutschen geil oder geile ab, einer Bezeichnung für den männlichen Hoden, und hat ursprünglich eine rein sexuelle Bedeutung: gierig nach sexueller Befriedigung sein, sexuell erregt sein [...]
(Brockhaus multimedial 2002)

MathematikerInnen, die ja sowieso scharf auf sind, empfinden (vermutlich für Laien unverständlich) bei solch einer Funktion wie der unten dargestellten "Weierstraßfunktion" ja tatsächlich sowas wie eine ästhetische und intellektuelle Lust!

MathematikerInnen haben aus puren Schönheitsempfinden eine Vorliebe für Funktionen, die zwei Kriterien erfüllen: sie sollen

1. "stetig" , d.h. "in einem Wusch" ohne Absetzen des Stifts zeichenbar und

2. "differenzierbar" sein, d.h. kein

"Zacken"

haben.

(vgl. auch ).

Schön in diesem Sinne ist also z.B.

• eine Parabel
   

• oder eine Sinusfunktion
  (die wir unten noch brauchen werden!).

Unschön sind hingegen so treffend benannte "Sägezahnfunktionen", also z.B.

Solche Funktionen sind etwa so anheimelnd wie

• eine Knochensäge

• oder ein Haifischgebiss .

MathematikerInnen (wie alle Menschen?) lieben also das Harmonisch-Gleitende statt des Abrupten (Unterbrechungen, radikale Umschwünge).

Die allermeisten Funktionen (und allemal - leider - sämtliche üblicherweise in der Schule durchgenommenen) legen nun aber die Vermutung nahe, dass eine Funktion,

• wenn sie die erste Bedingung erfüllt, also stetig ist,

• zumindest abschnittsweise auch die zweite Bedingung erfüllt, also differenzierbar ist:

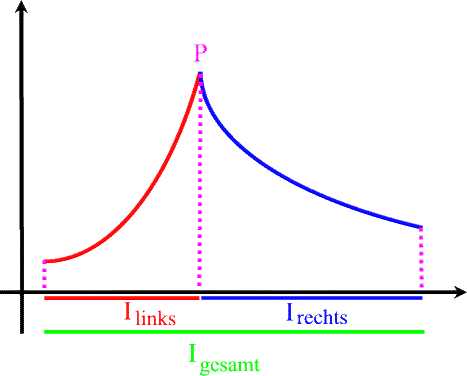
Die hier dargestellte stetige Funktion ist also

• zwar nicht auf dem Gesamtintervall I _gesamt differenzierbar, sondern hat ja in P eine "Zacke",

• aber sie ist es immerhin abschnittsweise

  • auf dem linken Teilintervall I _links

  • bzw. auf dem rechten Teilintervall I _rechts .

Und die MathematikerInnen sind es ja durchaus gewohnt, sich damit durchs Leben zu mogeln bzw. sich die "Wirklichkeit" damit hinzubiegen, dass sie nur Teilintervalle betrachten (den Definitionsbereich nach Lust und Laune einschränken).

(Natürlich machen die MathematikerInnen es sich da ohne alle Skrupel ein bisschen arg einfach. Es ist etwa so, als hielten sie den Nürburgring für eine sehr einfach zu fahrende Rennstrecke, weil sie die sogenannte "Müllenbach Schleife" nicht wahrhaben wollen:

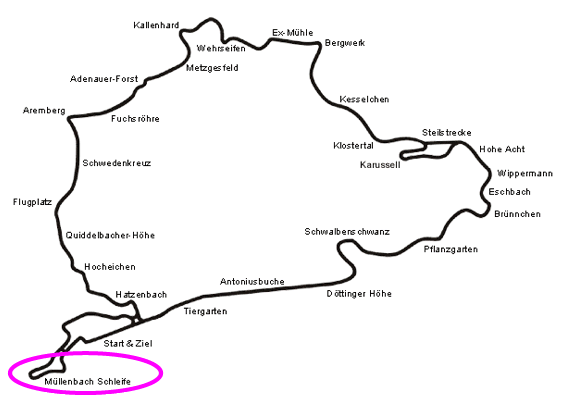
Aber solche Einschränkungen auf Teilintervalle sind eben doch oftmals praktisch und erkenntnisfördernd.)

Wenn also eine (stetige) Funktion mehrere Zacken hat, so könnte man doch meinen, dass man einfach immer nur die Teilintervalle zwischen den Zacken (die Zaunelemente zwischen den Zaunpfühlen) betrachten muss, und schon hat man zumindest auf diesen Teilintervallen jeweils differenzierbare Funktionen (und ist die "Welt" sozusagen wieder in Ordnung bzw. harmonisch).

Es scheint nun allem o.g. Harmonieempfinden krass zu widersprechen, wenn MathematikerInnen nach Funktionen suchen, die zwar die erste Bedingung (Stetitgkeit), aber nirgends die zweite (Differenzierbarkeit) erfüllen.

Da hört nun tatsächlich (vorerst) das visuell-harmonische Interesse auf und fängt ein intellektuelles Interesse an.

(Und solch ein intellektueller Zugang birgt für MathematikerInnen oftmals auch eine "innere" Schönheit und Vollkommenheit.)

MathematikerInnen reizt das reine intellektuelle Spiel, und sie denken: "anscheinend ist das ausgeschlossen, aber stimmt das denn wirklich?"

Und wenn es solch eine zwar durchaus stetige, aber nirgends differenzierbare Funktion gäbe, wäre doch zu fragen, wie sie aussehen könnte. Anscheinend müssten die "Zacken" doch unendlich nahe zusammen Rücken, damit

• die Teilintervalle dazwischen, auf denen die Funktion dennoch differenzierbar ist, immer FEINER würden und verschwänden

• und letztlich nur noch "Zacken" übrig blieben
  (man kann sich das etwa so vorstellen wie einen Zaun, der nur noch aus Zaunpfühlen besteht, zwischen denen keine Zwischenelemente mehr aufgehängt werden können).

Es müssten in jedem Bereich unendlich viele "Zacken" hautnah nebeneinander liegen.

Der große Mathematiker

Karl Weierstraß
(1815-1897),

dem immerhin auch der so treffende Satz

"Es ist unmöglich, ein Mathematiker zu sein, ohne die Seele eines Dichters zu haben"

zugeschrieben wird, hat tatsächlich solch eine äußerst exotische Funktion (oder genauer: eine ganze Klasse solcher Funktionen) aufgezeigt, und zwar z.B.

f(x) =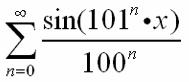

Die Funktion verhält sich erst mal ganz harmlos und konventionell, ihr Graph sieht nämlich auf den ersten Blick genauso aus wie ein Sinus, also der Inbegriff von stetig und differenzierbar (also o.g. harmonischen Schönheit):

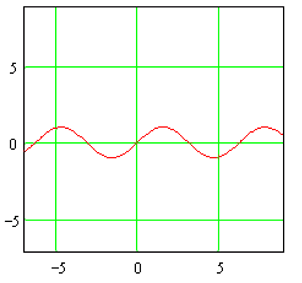
Der eigentliche "Gag" wird aber erst deutlich, wenn man den Graphen kontinuierlich vergrößert bzw. mit einer Art Kamerafahrt in ihn hinein zoomt:

Bei dieser Kamerafahrt zeigt sich, dass jeder anfänglich "glatte" Sinusbogen nochmals von feineren Sinusbögen Überlagert ist - und das unendlich so weiter bzw. immer feiner.

Der "Gag" besteht also darin, dass die Funktion nur scheinbar in einem Punkt P eine klare Steigung hat

,

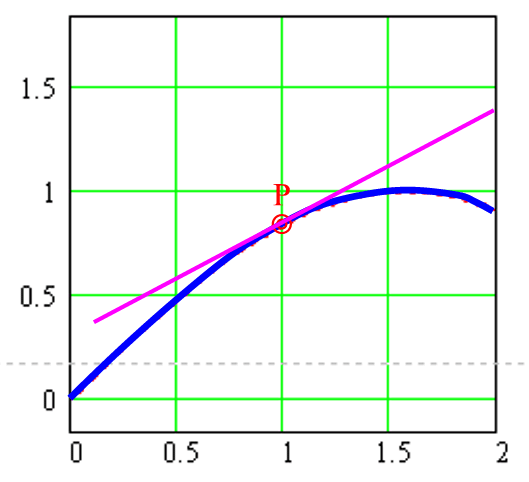da aber in einem ersten Vergrößerungsschritt schon wieder eine ganz andere Steigung vorliegt (und im zweiten Vergrößerungsschritt schon wieder eine ganz andere usw. usf.):

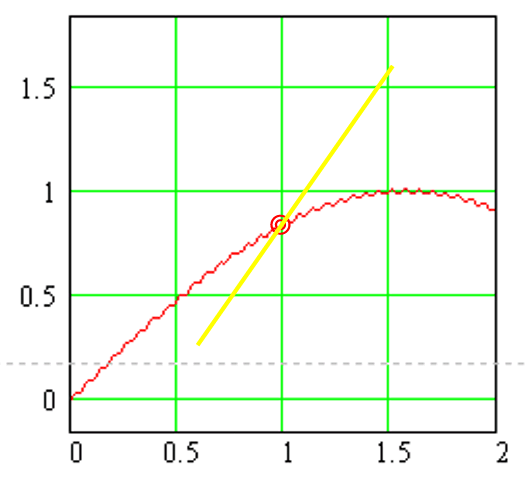
Jeder "Grobsinus" lässt sich also in einen "Feinsinus" auflösen.

(Wichtig dabei ist, dass eine unendliche Summe vorliegt: wäre das nicht der Fall, so gäbe es einen letzten Summanden, der die Steigung endgültig definieren würde, so dass also doch Differenzierbarkeit vorläge.)

An der Weierstraßfunktion ist mehrerlei bemerkenswert:

1. funktioniert sie schon wie die Fraktalgeometrie, bei der ja auch durch einen Zoom immer wieder (selbst-)ähnliche kleinere Strukturen sichtbar werden:

Und sowas vermittelt eine neue Schönheit, weil es natürlichen Prozessen viel näher liegt als die abgenagte sonstige Geometrie. Vgl. etwa Farne, bei denen der Hauptzweig ähnlich aussieht wie Nebenzweige und diese wiederum wie einzelne Blätter:

(wobei darauf hingewiesen sei, dass das kein echter Farn, sondern ein mathematisch erzeugter "Farn" ist)

2. Weierstraß ist teilweise denselben Weg gegangen wie wir oben, teilweise einen anderen:

• zwar hat auch er eine immer weitere VERFEINERUNG durchgeführt,

• aber er hat "Nicht-Differenzierbarkeit" anders verstanden, nämlich nicht über "Zacken"

(ich war oben bewusst so mathematisch unsauber vorgegangen, weil es einfach anschaulicher und näherliegender war).

D.h. ihm gelingt es, eine nirgends differenzierbare Funktion zu konstruieren und dennoch o.g. "zackenlose" Harmonie beizubehalten.

Die Funktion f(x) = behält also glücklicherweise ihren harmonisch-visuellen Reiz, der nur durch den intellektuellen Reiz ergänzt wird. Beide Aspekte müssen sich keineswegs gegenseitig ausschließen.

Als mittelmäßiger Mathematiker steht man staunend (oder geradezu andächtig) vor dieser Funktion und fragt sich, wie Weierstraß auf sie gekommen sein mag.

Nun ist es in der Mathematikgeschichte oftmals unbekannt, wie jemand zu seiner Erkenntnis gekommen ist: es werden oftmals nur die Fakten, nicht aber die Wege (und oftmals sogar nicht die Personen) überliefert, es zählt (leider) nur das Ergebnis.

(Und ich habe bisher noch keine Informationen dazu finden können, wie Weierstraß drauf gekommen ist.)

Aber der Weg lässt sich manchmal sozusagen "fiktiv rekonstruieren" (vgl.   ), und genau das will ich hier ansatzweise versuchen.

Eine häufige Frage in der Mathematikgeschichte ist, ob MathematikerInnen Sachverhalte erfinden oder entdecken:

• "erfinden" hieße, dass die Sachverhalte vorher nicht da waren und erst durch ihre Erfinder "auf die Welt kommen"
  (vgl.: Lilienthal hat das Flugzeug erfunden, denn vorher gab es noch keine Flugzeuge);

• "entdecken" hieße, dass die Sachverhalte vorher schon im Verborgenen schlummerten (noch unbekannt waren, aber schon zutrafen) und ihr "Entdecker" nur als erster auf längst Existentes aufmerksam wurde
  (vgl.: Amerika wurde [zumindest aus europäischer Sicht] von Columbus entdeckt, aber natürlich nicht erfunden: das gab's schon vorher - und war natürlich auch den Indianern längst bekannt).

Eins der berühmtesten mathematischen Beispiele ist "der Satz des Pythagoras", der besagt, dass für die Seiten a, b und c jedes rechtwinkligen Dreiecks der äußerst einfache Zusammenhang a² + b² = c² gilt (und umgekehrt).

(Wobei hier man unterstellt sei, was historisch keineswegs so gewiss ist, nämlich dass tatsächlich Pythagoras diesen Satz bewiesen hat.)

Mag ja sein, dass Pythagoras o.g. Zusammenhang als erster allgemeingültig bewiesen hat. Genau das zeigt aber doch,

• dass der Satz immer und jederzeit (nämlich für alle rechtwinkligen Dreiecke) gilt,

• also auch alle rechtwinkligen Dreiecke, die es vor Pythagoras gegeben hat.

Nur hat's keiner bemerkt. Oder genauer: den Zusammenhang haben schon die Babylonier gekannt, nur konnten sie ihn noch nicht beweisen

(bzw. hatten gar kein Beweisinteresse oder sahen gar keine Beweisnotwendigkeit?).

In diesem Sinne wäre Pythagoras also "nur" der Entdecker, nicht aber der Erfinder gewesen.

Umgekehrt ist Pythagoras aber der Erfinder zwar nicht des Zusammenhanges, aber doch des Beweises.

(Aber selbst bei den Grundlagen der Naturwissenschaften ist es ja nicht eindeutig klar, ob da erfunden oder entdeckt wird:

"[...] die [genetische] Struktur, die Watson und Crick vorgeschlagen haben, [enthält] auch eine kreative Komponente, wie sich jeder klarmachen kann, wenn er versucht, die Frage zu beantworten, wo denn die Doppelhelix war, bevor Watson und Crick sie gefunden haben. In einer Zelle sicher nicht, denn dort finden sich nur komplizierte Vermischungen und Verbindungen aus vielen Molekülen, die getrennt und in höchst künstliche Umgebungen gebracht werden müssen. Natürlich hat die vorgeschlagene Struktur des Erbmaterials eine Entsprechung in der molekularen Wirklichkeit der Zelle, aber wie diese Realität mit der des Modells zusammenhängt, das die berühmte Doppelhelix zeigt, stellt keinesfalls eine banale Frage dar. Die Doppelhelix ist sowohl Schöpfung als auch Entdeckung, und der Bereich ihres Daseins ist nicht die Natur (und erst recht nicht eine Zelle), sondern die Gedanken- und Bilderwelt der Kultur namens Naturwissenschaft."

[zitiert nach ] )

Im Hinblick auf die Weierstraßfunktion wäre also zu fragen:

• hat Weierstraß sie "nur" entdeckt, d.h. ist ihm anhand der bereits vorhandenen Funktion "nur" irgendwann aufgefallen, dass sie zwar stetig, aber nirgends differenzierbar ist?

• oder hat er sie erfunden, d.h. (systematisch) konstruiert?

Nun liegt solch eine relativ exotische Funktion wie

f(x) =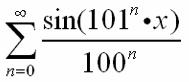

ja nicht einfach in der Landschaft rum, so dass Weierstraß über sie gestolpert und dann bei genauerem Hinsehen ihre besondere Eigenschaft entdeckt haben könnte

(dazu - so scheint mir - hätte er tatsächlich wie wir einen Computer mit Vergrößerungsmöglichkeiten gebraucht; s.u.).

Sondern jede Wette:

Aber wie?

(Zur Beantwortung dieser Frage werde ich im Folgenden nur einige wenige Details behandeln, also z.B. nicht die 101 im Zähler und die 100 im Nenner - was doch schwer danach aussieht, dass die 100 willkürlich gewählt und bei der 101 nur 1 addiert wurde; ich vermute also mal - ohne es genauer untersucht zu haben -, dass das Ganze z.B. auch für 58 im Nenner und 59 im Zähler funktioniert, womit sich die o.g. Klasse von [vielen] Funktionen ergäbe.)

Eine denkbare Vorgehensweise sieht man, wenn man die ersten beiden Glieder der unendlichen Reihe anschaut, also für n = 0 und n = 1:

• für n = 0 ergibt sich der erste Summand

,

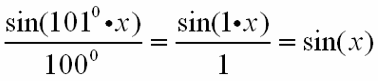d.h. die simple Sinusfunktion, die man ja auch in o.g. Animation am Anfang, d.h. noch ohne Vergrößerung sieht;

• für n = 1 ergibt sich der zweite Summand

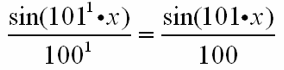
Daran ist im Vergleich mit dem ersten Summanden zweierlei neu:

1. die 101 im Zähler,

2. die 100 im Nenner.

Wenn man nun ein wenig die Anfangsgründe der Sinusfunktion kennt, so weiß man:

1. die 101 sorgt im Vergleich mit der ursprünglichen Sinusfunktion dafür, dass die neue Funktion 101 mal so schnell  "getaktet" ist, also eine erheblich höhere Frequenz hat bzw. sehr viel schneller hoch und wieder runter geht.

Und die 100 im Nenner sorgt dafür, dass

2. der Ausschlag nach oben und unten nicht mehr 1, sondern nur noch ein Hundertstel ist.

Der Funktionsgraph zu diesem zweiten Summanden ist also sowohl in horizontaler als auch in vertikaler Hinsicht viel feiner (bleibt aber eine sinusförmige Funktion).

Indem nun der zweite zum ersten Summanden addiert wird, wird der erste Sinusgraph, der weiterhin das grobe Aussehen (auf den ersten Blick) festlegt, mit dem viel feineren zweiten Sinusgraphen überlagert (was man dann nach dem ersten Vergrößerungsschritt sieht).

Genau das scheint Weierstraß also vorgehabt zu haben:

Man könnte auch sagen, dass Weierstraß eine extrem nervöse Funktion gesucht und gefunden hat: man kann noch so nah ran gehen, sie zittert immer.

Zumindest bei einer endlichen Anfangssumme (z.B. für n = 0 bis n = 10) ist dabei die unausweichliche Voraussetzung garantiert: als Summe stetiger Funktionen ist auch die Summenfunktion wieder stetig.

Als ich zum ersten Mal die Computeranimation sah, habe ich mich gefragt, wie Weierstraß überhaupt die Besonderheiten der Funktion (das immer kleinere Schwanken) entdecken (!) konnte, ohne einen Computerzu haben.

Erst jetzt im Nachhinein, also nach Rekonstruktion des Erfindungsweges, ist mir klar geworden, dass er gar keinen Computer und keine (wortwörtlich optische) Vergrößerung brauchte:

Die fiktive Rekonstruktion kann aber noch einen Schritt über den bloßen Nachvollzug hinausgehen. Ich würde mir jetzt zumindest zutrauen, nach dem Vorbild der Weierstraßfunktion selbst ganz andere solche (also zwar stetige, aber nirgends differenzierbare) Funktionen zu konstruieren.

Und solche ein pseudorealistische historische Rekonstruktion (oder eine ähnliche zu einem anderen Thema) scheint mir nicht nur in der Schule möglich, sondern auch dringend geboten, und zwar aus zwei Gründen:

1. , damit die SchülerInnen sehen, wie man "drauf kommen" kann,

2. , weil dabei besonders gut fachlich Wichtiges klar wird, nämlich im vorliegenden Beispiel der Begriff der Differenzierbarkeit dadurch besonders deutlich hervortritt, dass man ihn von seinem radikalsten Gegenteil (totaler Undifferenzierbarkeit) abgrenzt: es hat nicht nur (fast) jede Regel eine Ausnahme, sondern eine Regel wird oftmals erst durch ihre Ausnahmen verständlich.

Es ist zuguterletzt wohl kaum ein Zufall, dass ausgerechnet Weierstraß o.g. Funktion "gefunden" hat. Sondern er war ja maßgeblich an der stringenten Erfassung der Funktionenanalysis beteiligt

(und damit auch an der Herausbildung einer sehr einseitigen Mathematik; vgl. ),

womit es doch immerhin nahe lag, dass er alle denkbaren Möglichkeiten von Funktionen untersuchte.

PS:

"Die Schlangen-Linie halte ich für ein Buch für die dienlichste, und ich hatte schon in dieser Linie geschrieben, [...] ehe Tristram Shandy seine Manier en Ziczac oder Ziczac à double Ziczac bekannt machte, so ohngefähr: ." (Georg Christoph Lichtenberg) Dabei bedeutet "Ziczac à double Ziczac" wohl eine feinere Schlangenlinie, die einer groberen überlagert wird.)