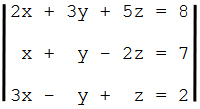
warum macht man sowas?:
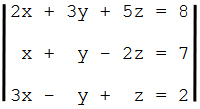
|
|
Eine Frau zum Arzt: "Ich habe einen
Knoten in der Brust." |
Irgendwann in der 7. oder 8. Klasse werden Gleichungssysteme
durchgenommen
(sogenannte 3x3-Gleichungssysteme),
also z.B.
2x + 3y + 5z = 8
x + y - 2z =
7
3x - y + z = 2
.
Was - zum Teufel - soll das?
Wenn man von an den Haaren herbeigezogenen eingekleideten Aufgaben absieht, gibt es dafür in der 7./8. Klasse keinerlei Anwendung, und zwar nicht mal innermathematische, da jede Einzelgleichung mit drei Variablen
(z.B. die erste, also 2x + 3y + 5z = 8)
die Gleichung einer Ebene im dreidimensionalen Raum ist, solche Ebenen aber noch nie Stoff der 7./8. Klasse waren und die Schüler auch wohl vollends überfordern würden.
Mit dem Gleichungssystem
E1: 2x
+ 3y + 5z = 8
E2:
x + y - 2z = 7
E3:
3x - y + z = 2
würde also die Schnittmenge der drei Ebenen E1 , E2 und E3 im Raum bestimmt, und in der Regel kommt bei sowas als Schnittmenge ein einzelner Schnittpunkt S heraus
(es gibt auch andere [evtl. leere] Lösungsmengen, aber mit Sonderfällen werde ich mich auch im Folgenden nicht beschäftigen).
Das Problem der Schnittmenge dreier Ebenen im Raum taucht allerdings in der Vektorgeometrie der Oberstufe nochmals auf und wird dann teilweise mit sogenannten "Matrizen"
(abgenagten Gleichungssystemen)
gelöst
(und da dann halte ich
[nachdem die Matrizenrechnung mal verstanden wurde]
den Einsatz von Taschenrechnern, die einem das Matrizenrechnen abnehmen, ausnahmsweise wirklich mal für sinnvoll):
 →
→
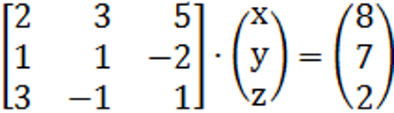
Nur werden die Schüler zwischen der 7./8. Klasse und der Oberstufe natürlich alles längst vergessen haben, was sie mal über Gleichungssysteme durchgenommen haben
(zumal Gleichungssysteme zwischendurch nie vorkommen),
so dass man in der Oberstufe diesbezüglich wieder bei Adam & Eva anfangen muss.
Sowieso ist es nicht gerade motivierend,
(eh nur innermathematisch)
später braucht,
Es muss also ganz andere Gründe geben, aus denen Gleichungssysteme aus drei Gleichungen mit drei Unbekannten in der 7./8. Klasse durchgenommen werden
(... wobei hier mal dahingestellt sei, ob das gute Gründe sind und eine Behandlung in der 7./8. Klasse dann doch rechtfertigen).
 kann auf
verschiedene Arten gelöst werden, die natürlich dennoch alle zum selben
Ergebnis führen
kann auf
verschiedene Arten gelöst werden, die natürlich dennoch alle zum selben
Ergebnis führen
Man wird aber schnell feststellen, dass diese unterschiedlichen Verfahren allzu leicht zu heilloser Verwirrung führen
(die Schüler wirklich mal durchleiden sollten!),
weshalb man vielleicht das unten durchgeführte totsichere

"Gaußsche Dreiecksverfahren"
zu schätzen lernen wird.
Um das Gaußsche Dreiecksverfahren verstehen zu können, schauen wir erstmal zurück auf zwei Gleichungen mit zwei Unbekannten
(sogenannte 2x2-Gleichungssysteme),
also z.B.
y = 3x + 5
y = - 4x - 2 .
Betrachten wir erstmal die beiden Gleichungen einzeln, also unabhängig voneinander:
Z.B. ergibt sich
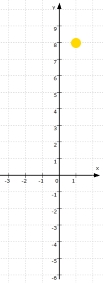 ,
,
 .
.
Da es unendlich viele x gibt, gibt es auch unendlich viele Punkte P (x|y), die alle zusammen die Gerade g bilden:
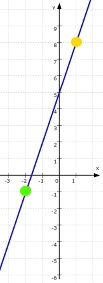
Z.B. ergibt sich
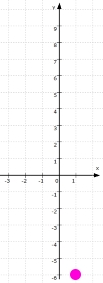 ,
,
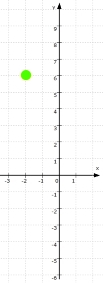 .
.
Da es unendlich viele x gibt, gibt es auch unendlich viele Punkte P (x|y), die alle zusammen die Gerade h bilden:

Halten wir also fest:
|
eine einzelne Gleichung mit zwei Unbekannten ist nicht (eindeutig) lösbar, sondern wir erhalten nur abhängig von jedem beliebigen x ein zugehöriges y. |
Betrachten wir nun aber die beiden Gleichungen
y = 3x + 5
y = - 4x - 2 .
zusammen, und zwar
liegen. Offensichtlich ist das nur der Schnittpunkt S:

| (Auf die Gefahr hin, dass es keiner bemerkt: für den Schnittpunkt S wurde natürlich mit Absicht die Mischfarbe Lila aus den beiden Geradenfarben blau und rot gewählt.) |
erfüllen.
Um diese x und y herauszufinden, setzen wir die beiden Gleichungen gleich und erhalten
3x + 5 = y = y = - 4x - 2
oder kurz
3x + 5 = - 4x - 2 .
Obwohl diese Gleichung so unscheinbar daherkommt, sollte man sie dennoch gebührend feiern:
Diese Gleichung enthält nun nämlich ENDLICH nur noch eine einzige Unbekannte, nämlich x. Damit wird plötzlich alles ganz einfach, denn nun können wir die Gleichung (eindeutig) lösen!:
3x + 5 = - 4x - 2 | + 4x
⇔7x + 5 = - 2 | - 5
⇔7x = - 7 | : 7
⇔ x = - 1
Kommen wir damit zurück zur ersten Gleichung y = 3x + 5. Erinnern wir uns:
mit dieser Gleichung können wir zu jedem beliebigen x das zugehörige y finden.
Also können wir auch zu x = - 1 das zugehörige y finden:
y = 3•(-1) + 5
Plötzlich enthält auch diese erste Gleichung nur noch eine einzige Unbekannte, nämlich y, d.h. wir können nun auch diese Gleichung (eindeutig) lösen:
y = - 3 + 5 = 2
oder kurz
y = 2 .
Damit können wir zur Geometrie zurückkehren und die exakten Koordinaten des Schnittpunkts S angeben:
S ( - 1 | 2 )
Halten wir insgesamt fest:
|
Gerade weil die meisten (Pseudo-)Anwendungsaufgaben zu 2x2-Gleichungssystemen nur an den Haaren herbeigezogene "eingekleidete" Aufgaben sind
(vordergründig geht es um lebensweltliche Anwendungen, in Wirklichkeit aber nur um die daraus destillierbare Mathematik),
scheint es mir "nur" innermathematische Gründe dafür zu geben, solche 2x2-Gleichungssysteme im Schulunterricht durchzunehmen:
|
es geht darum, mittels der 2x2-Gleichungssysteme (Funktions-)Gleichungen mit einer oder mehreren Unbekannten/Variablen noch (?) besser zu verstehen (und Funktionsgleichungen sind in der [Schul-]Mathematik nunmal extrem wichtig). |
Ich befürchte allerdings, dass die im Schulunterricht übliche Behandlung von 2x2-Gleichungssystemen meistens zum glatten Gegenteil von tieferem Verständnis führt, nämlich zu
"jetzt versteh' ich gar nix mehr!"
Wenn man dann in der 7./8. Klasse zu 3x3-Gleichungssystemen à la

übergeht, fallen für 7.-/8.-Klässler endgültig jeder geometrische Bezug und damit jede Anschaulichkeit weg.
(Bei 2x2-Gleichungssystemen gab's immerhin noch die Geraden-Vorstellung, bei 3x3-Gleichungssystemen steht 7.-/8.-Klässlern aber - wie oben bereits gesagt - die Ebenen-Vorstellung noch gar nicht zur Verfügung. Zudem sind Ebenen ja sowieso schwer vorstellbar, wenn man keine 3D-Koordinatensysteme zur Verfügung hat
[3D-Computeranimationen sind da sicherlich ansatzweise hilfreich, bleiben aber auf dem Computerbildschirm letztlich auch nur 2D].)
Bei 3x3-Gleichungssystemen bleibt 7.-/8.-Klässlern also nur noch das abstrakt algebraische Rumstochern - was ja noch lange kein Einwand gegen die Behandlung von 3x3-Gleichungssystemen im Unterricht der 7./8. Klasse ist!
Man kann es ja auch so sehen, dass das rein algebraische Rumstochern ein wichtiges, weil geradezu mathetypisches Ziel ist, das die Schüler unbedingt auch mal kennenlernen sollten:
dass man etwas (den Schnittpunkt dreier Ebenen) berechnen kann, obwohl man keine anschauliche Vorstellung (von den Ebenen) hat;
dass also die Algebra eine Raumsonde in das Universum jenseits des direkt Anschaulichen ist:

(Das Bestehen auf
ist ja letztlich
Spießerideologie, die selbst der Spießer nicht konsequent durchhält: bei seiner Vorliebe für Consense-Pop-Musik und gigantomanische action-Filme fragt er ja auch nicht nach einer Anwendbarkeit:
)
Man mag also das rein algebraische Vorgehen für wichtig halten, aber das lässt sich Schülern kaum vermitteln.
Ein anderer Grund für den Übergang von 2x2- zu 3x3-Gleichungssystemen ist der "Verallgemeinerungs-Wahn" der Mathematiker.
Ein Beispiel:
nach der Untersuchung sogenannter "ganzrationaler" Funktionen ersten Grades, also linearer Funktionen mit Funktionsgleichungen der Form y = bx + a bzw. y = bx1 + a,
stellt sich für Mathematiker natürlich umgehend die Frage, welche Eigenschaften Funktionen zweiten Grades, also mit Funktionsgleichungen der Form y = cx2 + bx + a, haben,
und welche Eigenschaften Funktionen dritten Grades, also mit Funktionsgleichungen der Form y = dx3 + cx2 + bx + a, haben,
... vierten ...,
... fünften ...,
... n-ten ..., wobei n irgendeine natürliche Zahl ist
(z.B. n = 137 291 884 123).
Aus demselben "Verallgemeinerungs-Wahn" interessieren sich Mathematiker
nach den 2x2-Gleichungssystemen für
3x3-Gleichungssysteme,
4x4-Gleichungssysteme,
5x5-Gleichungssysteme,
... ,
nxn-Gleichungssysteme.
Am interessantesten sind solche Verallgemeinerungen, wenn man ein Lösungsverfahren für sehr viele oder gar alle möglichen Fälle entdecken kann. Und in der Tat ist das unten an 3x3-Gleichungssystemen entwickelte "Gaußsche Dreiecksverfahren" (s.u.) ein hilfreicher Lösungsweg für (fast) alle Gleichungssysteme.
Nun aber langsam zur Lösung des 3x3-Gleichungssystems
2x + 3y + 5z = 8 A
x + y - 2z = 7 B
3x - y + z = 2 C :
jede der drei Gleichungen A, B und C enthält die drei Variablen x, y und z. Was das bedeutet, machen wir uns mal exemplarisch an der Gleichung C klar. Dazu formen wir diese Gleichung C ein wenig um:
3x - y + z = 2 | - 3x + y
⇔ z = 2 - 3x + y
Damit haben wir eine Arbeitsanweisung, wie aus vorgegebenen x und y das zugehörige z berechnet werden kann:
man kann für x völlig frei eine beliebige Zahl auswählen, also z.B. x = 5;
man kann für y ebenfalls völlig frei eine beliebige Zahl auswählen, also z.B. y = 12;
für z hingegen hat man jetzt keine freie Wahl mehr, sondern es ergibt sich zwingend
z = 2 - 3•x + y =
= 2 - 3•5 + 12 =
= 2 - 15 + 12 = -1
oder kurz z = -1.
Geometrisch gesagt: der Punkt P ( 5 | 12 | - 1 ) liegt in der Ebene E3 mit der Funktionsgleichung 3x - y + z = 2 .
(Aber er liegt z.B. nicht in der Ebene E2 : x + y - 2 z = 7, denn
5 + 12 - 2•(-1) =
= 5 + 12 + 2 =
= 19 ≠ 7.)
Es gilt also analog zu den 2x2-Gleichungssystemen:
|
Beim Gleichungssystem
2x + 3y + 5z = 8 A
x + y - 2z = 7 B
3x - y + z = 2 C
muss es also unser Ziel sein,
|
Kurz zur Schreibweise:
beim Umformen von Gleichungen eines 3x3-Gleichungssystems sollte immer klar bleiben, welche drei Gleichungen das 3x3-Gleichungssystem bilden, denn sonst verliert man beim Untereinanderschreiben von massenhaft Gleichungen doch allzu leicht die Übersicht, welche jeweils drei Gleichungen zusammen gehören.
Um die Zusammengehörigkeit von je drei Gleichungen zu verdeutlichen, haben sich verschiedene Schreibweisen durchgesetzt:
: man fügt (wie z.B. in
![]() ) nach je drei Gleichungen eine Leerzeile
ein;
) nach je drei Gleichungen eine Leerzeile
ein;
: man macht links und rechts von je drei
Gleichungen lange Striche:
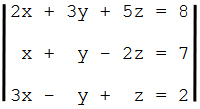 ;
;
: man macht vor je drei Gleichungen eine
dreiecksförmige Klammer: 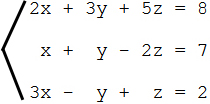 ;
;
: man macht unter je drei Gleichungen einen
Querstrich:
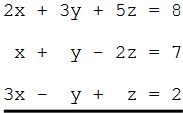 .
.
Ich werde im Folgenden der Einfachheit halber die 4. Möglichkeit (also Querstriche) anwenden.
Aber zurück zu unserem Ziel,
|
Wir gehen das Ziel in kleinen "Häppchen" an, indem wir
erstmal aus der zweiten und dritten Gleichung die Unbekannte x rauswerfen,
in der zweiten und dritten Gleichung also nur noch die beiden Unbekannten y und z haben.
Dazu sorgen wir erstmal dafür, dass in allen drei Gleichungen gleich viele x vorhanden sind
(nebenbei: die Gleichungen werden des öfteren mit Buchstaben [A, B, C ...] benannt, damit man kurz notieren kann, wenn zwei Gleichungen gleichzeitig benutzt werden;
z.B. bedeutet A + B dann, dass die beiden Gleichungen A und B komplett addiert werden;
wichtig dabei ist, dass nicht ein Buchstabe zweimal für verschiedene Gleichungen benutzt wird):
2x + 3y + 5z = 8 A |•3
x + y - 2z = 7 B |•6
3x - y + z = 2 C |•2
___________________
6x + 9y + 15z = 24 D
6x + 6y - 12z = 42 E
6x - 2y + 2z = 4 F
___________________
6x + 9y + 15z = 24 D
3y + 27z = -18 D - E
11y + 13z = 20 D - F
Damit ist unser erstes Teilziel erreicht, in der zweiten und dritten Gleichung nur noch die beiden Unbekannten y und z zu haben. Da, wo in den beiden Gleichungen vorher noch die Unbekannte x stand, steht nun nichts mehr:

Der nächste Teilschritt ist nun, aus der dritten Gleichung auch noch die Unbekannte y rauszuwerfen, so dass sie dann nur noch die Unbekannte z enthält. Dazu sorgen wir erstmal dafür, dass in in der zweiten und dritten Gleichungen gleich viele y vorhanden sind:
6x + 9y + 15z = 24 D
3y + 27z = -18 |•11
11y + 13z = 20 |• 3
_____________________
6x + 9y + 15z = 24 D
33y + 297z = -198 G
33y + 39z = 60 H
_____________________
6x + 9y + 15z = 24 D
33y + 297z = -198 G
258z = 258 G - H
Damit ist unser erstes Hauptziel erreicht, in einer Gleichung (der dritten) nur noch eine einzige Unbekannte (hier z) zu haben.
Da, wo in der dritten Gleichungen vorher noch die Unbekannte y stand, steht nun nichts mehr:

Damit haben wir
die Stufenform 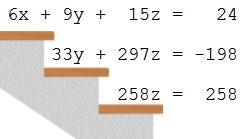 bzw.
bzw.
das Gaußsche Dreieck 
erreicht.
Da nun aber in der dritten Gleichung nur noch die eine Unbekannte z vorkommt, besteht wieder Anlass zu allergrößter Freude:
Nun können wir nämlich z ausrechnen:
6x + 9y + 15z = 24 D
33y + 297z = -198 G
258z = 258 |: 258
______________________
6x + 9y + 15z = 24 D
33y + 297z = -198 G
z = - 1 J
Um jetzt auch noch
erst die Unbekannte y und
später die Unbekannte x
zu berechnen, setzen wir in den ersten beiden Gleichungen für die z den nun aus der dritten Gleichung bekannten Wert -1 ein und erhalten
6x + 9y + 15•(-1) = 24 J in D
33y + 297•(-1) = -198 J in G
z = - 1 J
__________________________
6x + 9y - 15 = 24 K
33y - 297 = -198 L
z = - 1 J
Damit haben wir auch in der zweiten Gleichung L nur noch die eine Unbekannte y
(und in der ersten Gleichung K immerhin nur noch die beiden Unbekannten x und y),
so dass wir nun auch y ausrechnen können:
6x + 9y - 15 = 24 K
33y - 297 = -198 | + 297
z = - 1
________________________
6x + 9y - 15 = 24 K
33y = 99 | : 33
z = - 1
________________________
6x + 9y - 15 = 24 K
y = 3 M
z = - 1
Um jetzt auch noch die Unbekannte x rauszubekommen, setzen wir in die erste Gleichung für y den nun bekannten Wert 3 ein und erhalten
6x + 9•3 - 15 = 24 M in K
y = 3 M
z = - 1
Nun enthält die erste Gleichung nur noch die eine Unbekannte x, die wir somit zuguterletzt auch noch ausrechnen können:
6x + 27 - 15 = 24
y = 3
z = - 1
__________________________
6x + 12 = 24 | - 12
y = 3
z = - 1
__________________________
6x = 12 | : 6
y = 3
z = - 1
__________________________
x = 2
y = 3
z = - 1
Damit haben wir alle drei (inzwischen nicht mehr) Unbekannten x, y und z berechnet!:
(Nebenbei: die ziemlich großen Zahlen, die sich während der Rechnungen durch das mehrfach Multiplizieren ergeben hatten, waren nur Zwischenstadien, denn für x, y und z kommen am Ende dennoch sehr einfache kleine Zahlen heraus.)
Die letzten drei Gleichungen hatten die Form
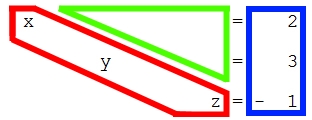 :
:
(und jetzt steht auch darüber nichts mehr);
Inzwischen könnte auch klar geworden sein, weshalb wir immer drei Gleichungen mitgeschleppt haben: wir hatten dadurch immer alles parat, um alle drei Unbekannten x, y und z auszurechnen.
Das Mitschleppen von immer drei (teilweise sogar unveränderten) Gleichungen ist nun zwar eine Menge Schreibarbeit, aber, liebe Schüler, lasst es Euch von einem langgedienten & altersweisen Lehrer sagen: wer zu faul für diese Schreibarbeit ist, wird schnell den Überblick verlieren - und deshalb letztlich mehr Fehler machen und mehr Zeit brauchen.
Ein Ziel der Beschäftigung mit 3x3-Gleichungssystemen ist es wohl, dass die Schüler mal ein idiotensicheres Lösungsverfahren
(hier das Gaußsche Dreiecksverfahren)
kennen und handzuhaben lernen. Wichtiger noch als die Handhabung scheint es mir allerdings, überhaupt das systematische Vorgehen zu verstehen:
1. Gleichung mit den Unbekannten x und y und z
2. Gleichung mit den Unbekannten x und y und z
3. Gleichung mit den Unbekannten x und y und z
_______________________________________
1. Gleichung mit den Unbekannten x und y und z
2. Gleichung mit den Unbekannten y und z
3. Gleichung mit den Unbekannten . y und z
_______________________________________
.

_______________________________________
1. Gleichung mit den Unbekannten x und y
2. Gleichung mit der Unbekannten y ← eine einzige Unbekannte, daher lösbar
3. Gleichung mit der Unbekannten z
_______________________________________
.

Insgesamt ist das, als wenn man eine Treppe erst hintunter und dann wieder hinauf steigt:

Dringend anzuraten ist auch das Untereinanderrechnen, weshalb hier alle Rechnungen nochmal in einem Schnelldurchlauf untereinander gezeigt werden:
2x + 3y + 5 z = 8 A |•3
x + y - 22 z = 77 B |•6
3x - y + z = 2 C |•2
_________________________
6x + 9y + 15 z = 24 D
6x + 6y - 2z2 z = 42 E
6x - 2y + 2 z = 4 F
_________________________
6x + 9y + 15 z = 24 D
3y + 27 z = - 18 D - E |•11
11y + 13 z = 20 D - F |• 3
_________________________
6x + 9y + 15 z = 24 D
33y + 297 z = -198 G
33y + 39 z = 60 H
_________________________
6x + 9y + 15 z = 24 D
33y + 297 z = -198 G
258 z = 258 G - H |: 258
_________________________
6x + 9y + 15 z = 24 D
33y + 297 z = -198 G
z = - 1 J
_________________________
6x + 9y + 15•(-1) = 24 J in D
33y + 297•(-1) = -198 J in G
z = - 1 J
_________________________
6x + 9y - 15 = 24 K
33y - 297 = -198 L |+ 297
z = - 1 J
_________________________
6x + 9y - 15 = 24 K
33y = 99 | : 33
z = - 1
_________________________
6x + 9y - 15 = 24 K
y = 3 M
z = - 1
_________________________
6x + 9•3 - 15 = 24 M in K
y = 3 M
z = - 1
_________________________
6x + 27 - 15 = 24
y = 3
z = - 1
_________________________
6x + 12 = 24 | - 12
y = 3
z = - 1
___________________________
6x = 12 | : 6
y = 3
z = - 1
__________________________
x = 2
y = 3
z = - 1
Da kann man jederzeit herausfinden, was man vorhatte - und ob man es auch tatsächlich (korrekt) durchgeführt hat.
Mit
dienen Gleichungssysteme insbesondere dem zweifelsohne nicht gerade beliebten Lernziel
![]() .
.