das wolln wa doch mal sehn,
ob wir den "Hypothesentest" kapieren

Vorweg: im Folgenden ist strikt zu unterscheiden zwischen der nur BEHAUPTETEN Wahrscheinlichkeit p1, mit der der Schütze trifft                         (und wenn der Schütze dann getroffen HAT, kann von Wahrscheinlichkeit gar keine Rede mehr sein), der Wahrscheinlichkeit p2, mit der wir richtige Aussagen über seine Fähigkeiten machen. reite ich vielleicht allzu sehr auf der UNsicherheit all unserer Bemühungen herum: "There's nothing sure in this world, There's nothing pure in this world."  In Wirklichkeit erstaunt mich aber, was mir geradezu paradox erscheint: dass wir über rein zufällige Ereignisse dennoch "ziemlich sichere" Urteile fällen können.

---

Der Hypothesentest wird im Folgenden zwar erst allgemein behandelt, die konkreten Rechnungen werden aber nur anhand von Binomialverteilungen durchgeführt.

Daraus folgt:

• die allgemeinen Betrachtungen kann man vermutlich auch ohne sonderliche Vorkenntnisse verstehen,
• für die Rechnungen muss man aber Vorkenntnisse zur Binomialverteilung haben

(und diese Kenntnisse zu Binomialverteilungen habe ich erst seit

);

insbesondere weiß ich seitdem erst, dass die Binomialverteilungen im Schulunterricht eine so große Rolle spielen,

• weil sie häufig bei Anwendungsaufgaben vorkommen,
• vor allem aber aus dem innermathematischen Grund, dass sich bei ihnen viele Rechnungen [!] erheblich verkürzen/vereinfachen - und somit die "eingekleideten" [Pseudo-]Anwendungsaufgaben oftmals nur Vorwand sind).

---

1. allgemeiner Teil:

gehen wir mal von folgendem Beispiel aus:

"Ein Sportschütze behauptet von sich, dass er ein regelrechter Profi ist und mit einer Wahrscheinlichkeit von p = 0,9 ins Schwarze trifft.
Um herauszufinden, ob seine Behauptung stimmt oder er nur ein Angeber ist, wird ein Probeschießen von 10 Schüssen vereinbart.
Der Sportschütze trifft bei diesem Probeschießen

1. 8 mal,
2. 3 mal.

Hat er im Fall a. bzw. b. bewiesen, dass er

1. tatsächlich so gut schießt,
2. keineswegs so gut schießt,

wie er behauptet hat?"

Zu allererst muss man sich hier klar machen, dass es sich um ein echtes Wahrscheinlichkeitsexperiment handelt:

• angenommen mal, der Sportschütze trifft üblicherweise mit der Wahrscheinlichkeit p = 0,9, ist also tatsächlich ein guter Schütze; dann kann es

(auch wenn es durchaus unwahrscheinlich ist)

dennoch durchaus passieren, dass er

(z.B. wegen ungünstiger Bedingungen oder weil er einen "schlechten Tag" hat)

nur 3 mal trifft - also fälschlich als Angeber dasteht;

• angenommen nun aber, der Sportschütze ist tatsächlich nur ein Angeber und trifft in Wirklichkeit üblicherweise nur mit der Wahrscheinlichkeit p = 0,4; dann kann es dennoch passieren, dass er "unverschämtes Glück" oder einen ungewöhnlich guten Tag hat

("auch ein blindes Huhn findet mal ein Korn"),

also zu Unrecht nicht als Angeber dasteht, sondern man ihm seine Selbstwertung glaubt.

Daraus folgt:

• nicht nur die Trefferhäufigkeit

(sowohl eines guten wie eines schlechten Schützen)

ist wahrscheinlichkeitsbedingt,

• sondern auch unsere Aussagen über den Schützen sind wahrscheinlichkeitsbedingt: wir können uns nach 10 (oder auch mehr) Schüssen im Probeschießen nie wirklich sicher sein, ob unsere Wertung

("tatsächlich guter Schütze" oder "Angeber")

stimmt, sondern

(und genau darauf laufen Hypothesentests hinaus!)

nur mit einer gewissen Wahrscheinlichkeit sagen, ob unsere Wertung richtig ist.

So ganz nebenbei haben wir hier auch schon, wenn auch bislang indirekt, den Fehler 1. und den Fehler 2. Art erwähnt:

• Wenn wir als notorische Menschenfreunde allen Menschen vorsorglich gutgläubig entgegentreten

(oder konkreten Anlass haben, dem Schützen zu glauben), 

 wenn also die (Null-)Hypothese H₀

"der Schütze trifft tatsächlich mit der Wahrscheinlichkeit p = 0,9"
bzw.
"er ist kein Angeber"

lautet, so gibt es zwei mögliche Fehler:

• ein möglicher Fehler besteht darin, dass
• der Schütze zwar üblicherweise tatsächlich mit der Wahrscheinlichkeit p = 0,9 trifft

(also sonst wirklich so gut ist, wie er behauptet), 

• im Probeschießen aber zufällig derart selten, dass wir ihn fälschlich für einen Angeber halten.

Dieser Fehler besteht also darin, dass

• wir dem Schützen (nämlich einen Könner) grob unrecht tun,
•  die Wahrheit fälschlich nicht erkannt wird.

• Ein  anderer möglicher Fehler besteht darin, dass
  • der Schütze in Wirklichkeit nur mit einer viel kleineren Wahrscheinlichkeit als p = 0,9 trifft

(also sonst viel schlechter ist, als er behauptet), 

• im Probeschießen aber zufällig doch derart häufig, dass wir ihn fälschlich für keinen Angeber halten, sondern ihm seine Selbstwertung glauben

Dieser andere Fehler besteht also darin, dass

• wir den Schützen (nämlich einen Angeber) zu gut behandeln,
• die Unwahrheit  fälschlich nicht erkannt wird.

• Wenn wir hingegen als notorische Misanthropen allen Menschen grundsätzlich misstrauisch gegenübertreten

(oder konkreten Anlass haben, dem Schützen zu misstrauen),

wenn also die (Gegen-)Hypothese H₁

"der Schütze trifft nicht mit der Wahrscheinlichkeit p = 0,9
[sondern einer geringeren Wahrscheinlichkeit]"
bzw.
"er ist ein Angeber"

lautet, so gibt es wieder zwei mögliche, wenn auch anders gelagerte Fehler:

• ein Fehler besteht jetzt darin, dass

• der Schütze zwar üblicherweise nicht mit der Wahrscheinlichkeit p = 0,9 trifft

(also sonst nicht so gut ist, wie er behauptet), 

• im Probeschießen aber zufällig derart häufig, dass wir ihn fälschlich für keinen Angeber halten, sondern ihm seine Selbstwertung glauben.

Dieser Fehler besteht hier also darin, dass

• wir dem Schützen (nämlich einen Angeber) zu gut behandeln,
• die Unwahrheit fälschlich nicht erkannt wird.

• Ein anderer möglicher Fehler besteht hier darin, dass
  • der Schütze in Wirklichkeit tatsächlich mit der Wahrscheinlichkeit p = 0,9 trifft

(also sonst wirklich so gut ist, wie er behauptet),  

• im Probeschießen aber zufällig doch derart selten, dass wir ihn fälschlich für einen Angeber halten.

Dieser andere Fehler besteht hier also darin, dass

• wir dem Schützen (nämlich einen Könner) grob unrecht tun,
• die Wahrheit fälschlich nicht erkannt wird.

Diese verzwickten bis geradezu haarspalterischen Alternativen sind nun aber (zumindest für mich) der Hauptgrund, warum der Hypothesentest so schwierig oder genauer: kaum zu merken ist

(oder es zumindest für mich bislang war).

Es wird also Zeit, ein bisschen Ordnung in dieses Kuddelmuddel zu bringen, was allerdings auf zwei Arten möglich ist:

1. Unterscheidungsmöglichkeit:

• "dass wir dem Schützen [nämlich einem echten Könner] grob unrecht tun",
• "dass wir dem Schützen [nämlich einen Angeber]           zu gut behandeln",

Hier könnte man sich fragen, was da der größere moralische Fehler ist, und ich würde dazu neigen, den ersten Fehler als schlimmer anzusehen

(vgl. das Problem, ob man

• einen des Mordes Unschuldigen versehentlich zu einer hohen Gefängnisstrafe verurteilt,
• einen des Mordes    Schuldigen versehentlich frei laufen lässt.

Es ist keine leichte Entscheidung und doch geradezu rechtsstaatlicher Grundsatz, dass Ersteres schlimmer als Letzteres ist, und dementsprechend könnte man Ersteres einen "Fehler 1. Art" und Letzteres einen "Fehler 2. Art" nennen).

Nun ist "Moral" allerdings (leider?) kein mathematisches Kriterium, und deshalb kommen wir zur zweiten Sortiermöglichkeit, die nebenbei (s.o.) nicht mit der ersten, moralischen übereinstimmt:

2. Unterscheidungsmöglichkeit:

wir unterscheiden nach dem Wahrheitsgehalt

(wobei man Wahrheit ja allerdings auch für einen moralischen Wert halten kann),

also zwischen

• die    Wahrheit wird fälschlich nicht erkannt,
• die Unwahrheit wird fälschlich nicht erkannt.

Und dafür hat man nunmal die Namen/Reihenfolge gewählt:

• Fehler 1. Art: die    Wahrheit wird fälschlich nicht erkannt,
• Fehler 2. Art: die Unwahrheit wird fälschlich nicht erkannt.

Schon haben wir aber das nächste Problem: wie kann man sich diese Reihenfolge merken?

Vielleicht eben doch, wie schon angedeutet, wieder moralisch:

• die Wahrheit steht moralisch höher als die Unwahrheit, und deshalb ist "die Wahrheit wird fälschlich nicht erkannt" der schlimmere und wichtigere Fehler, also der "Fehler 1. Art";
• oder nehmen wir wieder das Beispiel eines des Mordes "Unschuldigen / Schuldigen": in beiden Fällen ist es doch wohl  (?) schlimmer, wenn die Wahrheit fälschlich nicht erkannt wird, also

1. der Unschuldige zu Unrecht ins Gefängnis wandert oder gar hingerichtet wird,
2. der      Schuldige zu Unrecht frei bleibt (uns dann weitere Morde begeht?).

und deshalb ist es auch hier sinnvoll,  "die Wahrheit wird fälschlich nicht erkannt" als "Fehler 1. Art" zu bezeichnen.

Auffällig bei unserer gesamten Argumentation ist,

dass wir grundsätzlich strikt zwischen der Wahrheit / Wirklichkeit (die nichts mit Zufall zu tun hat!: der Schütze ist tatsächlich entweder ein Könner oder ein Angeber) und unserer Einschätzung (die wir aufgrund eines eben doch teilweise durch Zufall bedingten Experiments [im vorliegenden Fall ein Probeschießen] aufstellen) unterscheiden. Das Problem dabei ist, dass wir (zumindest in unserem kurzen Experiment = Probeschießen) die Wahrheit gar nicht kennen, sondern nur Indizien für sie sammeln können. D.h. aber eben auch, dass wir mit unserer aus dem Experiment gebildeten Einschätzung grob daneben liegen können, indem wir beispielsweise einen Könner der Angeberei verdächtigen oder einem Nichtskönner seine Angebereien glauben. Radikaler formuliert: wir können über die Wahrheit grundsätzlich nichts aussagen, sie ist uns völlig unzugänglich. Vielmehr können wir nur Einschätzungen vornehmen, die aber eben auch falsch sein können   (wobei sich allerdings das kleine, aber feine logische Problem ergibt, woran wir das messen wollen, wenn die Wahrheit unzugänglich ist). Dass aber die Wahrheit vielleicht nicht zugänglich ist und dass Einschätzungen nunmal notgedrungen daneben liegen können, enthebt uns ja nicht dieser unvermeidlichen Einschätzungen, und da wollen wir im Folgenden doch wissen (und das ist der eigentliche Sinn der Hypothesentests!), mit welcher Wahrscheinlichkeit wir richtig oder aber daneben liegen. (Man beachte den subtilen Widerspruch "wissen/Wahrscheinlichkeit", hinter dem sich ein Grundproblem der Wahrscheinlichkeitsrechnung bzw. ihr größtes Wunder verbirgt: über den Zufall eben doch halbwegs verlässliche Aussagen machen zu wollen/können.) Anders gesagt: entbehren unsere Einschätzungen jeglicher Grundlagen oder können wir sie mit einiger Verlässlichkeit aufstellen? Konkreter: bei welchem Ausfall des Probeschießens können wir immerhin halbwegs begründet sagen, dass der Schütze ein Könner oder aber ein Angeber ist? (... wobei wir - nochmals gesagt - immer im Hinterkopf behalten, dass unser Urteil trotz größten Bemühens um Gerechtigkeit falsch sein kann.)

Bislang haben wir uns arg negativ nur um die Möglichkeiten gekümmert, (unvermeidbare!) Fehler zu begehen. Werden wir also mal positiver:

natürlich können wir mit unseren Einschätzung auch richtig liegen, können die Einschätzungen also mit der Wahrheit übereinstimmen: aufgrund des Probeschießens nehmen wir zu Recht an, dass der Schütze

• ein sehr guter Schütze ist,
• oder aber ein Angeber.

Das können wir oftmals sogar intuitiv einschätzen, also ohne Mathematik:

• wenn der Schütze 8 mal trifft, so werden wir ihn als guten Schützen einschätzen, selbst wenn er einmal weniger getroffen hat als sonst im Schnitt,
• wenn der Schütze 3 mal trifft, werden wir ihn als Angeber einschätzen

(und können doch, wie inzwischen vielfach gezeigt, in beiden Fällen falsch liegen).

Insgesamt ergibt sich damit folgendes Schema:

			Wahrheit
			Hypothese ist wahr ("der Schütze ist  in Wirklichkeit ein Könner")	Hypothese ist falsch ("der Schütze ist in Wirklichkeit ein Angeber")
	Hypothese (z.B. "der Schütze ist ein Könner") wird ...	... angenommen, d.h. die Hypothese scheint durch das Experiment bestätigt ("der Schütze ist ein Könner")	richtige Entscheidung ("der Schütze ist tatsächlich ein Könner")	Fehler 2. Art ("der Schütze wird fälschlich als Könner angesehen")
		... abgelehnt, d.h. die Hypothese scheint durch das Experiment widerlegt ("der Schütze ist ein Angeber")	Fehler 1. Art ("der Schütze wird fälschlich als Angeber angesehen")	richtige Entscheidung ("der Schütze ist tatsächlich ein Angeber")
		↑ erster Schritt nach dem Experiment (Probeschießen), Entscheidung für oder gegen die anfängliche Hypothese	↑ zweiter Schritt nach dem Experiment: Überlegungen, ob die Entscheidung für oder gegen die Hypothese richtig oder falsch war
	↑ vor dem Experiment (Probeschießen)	↑ nach dem Experiment (Probeschießen)

Oder allgemein, dafür aber sehr knapp:

			Wahrheit
			Hypothese ist wahr	Hypothese ist falsch
	Hypothese wird ...	... angenommen	richtige Entscheidung	Fehler 2. Art
		... abgelehnt	Fehler 1. Art	richtige Entscheidung

Wichtig daran ist insbesondere Folgendes:

1. dass wir die Anfangshypothese vor dem Experiment aufstellen müssen, dass sie also ohne Vorinformationen getroffen wird und somit arg "gefühlsbedingt" ist;
2. wir kommen nicht um eine "wertende" Anfangshypothese drum herum, also z.B.

• weil ich ein gutgläubiger Menschenfreund bin oder beim konkreten Schützen Anlass dazu habe, unterstelle ich, dass er tatsächlich ein guter Schütze ist und mit der Wahrscheinlichkeit p = 0,9 trifft

(seine konkreten Treffer können mich immer noch zur Überzeugung bringen, dass er also trotz gegenteiliger Anfangsannahme eben doch ein Angeber ist),

oder

• weil ich ein Misanthrop bin oder beim konkreten Schützen Anlass dazu habe, unterstelle ich, dass er ein Angeber ist und nicht mit der Wahrscheinlichkeit p = 0,9, sondern z.B. nur mit der Wahrscheinlichkeit p = 0,3 treffen wird

(seine konkreten Treffer können mich immer noch zur Überzeugung bringen, dass er also trotz gegenteiliger Anfangsannahme eben doch ein Könner ist).

3. Die Angangshypothese ("er ist ein Könner" oder "er ist ein Angeber") abzulehnen, bedeutet gleichzeitig, die Gegenhypothese ("er ist ein Angeber" oder "er ist ein Könner") anzunehmen: wir ändern also unsere Meinung.
4. Wir erfahren nie die Wahrheit, sondern können uns nachträglich nur klar machen, dass wir richtig oder falsch entschieden haben können und welche Art Fehler wir eventuell gemacht haben (und mit welcher Wahrscheinlichkeit).
5. Wenn wir anfangs von der Gegenhypothese "der Schütze ist ein Angeber" ausgehen, fallen die beiden Fehler "andersrum" aus:

			Wahrheit
			Hypothese ist wahr ("der Schütze ist  in Wirklichkeit ein Angeber")	Hypothese ist falsch ("der Schütze ist in Wirklichkeit ein Könner")
	Hypothese (z.B. "der Schütze ist ein Angeber") wird ...	... angenommen, d.h. die Hypothese scheint durch das Experiment bestätigt ("der Schütze ist ein Angeber")	richtige Entscheidung ("der Schütze ist tatsächlich ein Angeber")	Fehler 2. Art ("der Schütze wird fälschlich als Angeber angesehen")
		... abgelehnt, d.h. die Hypothese scheint durch das Experiment widerlegt ("der Schütze ist ein Könner")	Fehler 1. Art ("der Schütze wird fälschlich als Könner angesehen")	richtige Entscheidung ("der Schütze ist tatsächlich ein Könner")

Kommen wir nun aber zu einem Wunsch, der oben schon genannt worden war, nämlich dem, halbwegs sichere Urteile zu fällen.

Eine Möglichkeit besteht darin, ein positives Urteil

("der Schütze ist ein Könner")

dann zu fällen, wenn die Ergebnisse des Experiments = Probeschießens nicht "allzu sehr" (???)  vom Erwarteten  abweichen, wenn sie also in einem gewissen Bereich um den Erwartungswert herum liegen, der sich aus meiner Anfangsannahme ergibt

(z.B. "ich glaube dem Schützen wohlwollend, dass er ein Könner ist, dass also p = 0,9 ist").

Dieser Bereich soll symmetrisch um den Erwartungswert liegen, also bei obigem zehnfachen Probeschießen mit der Wahrscheinlichkeit p = 0,9 folgendermaßen:

(Es sei ergänzt, dass wir hier einen merkwürdigen Trick anwenden: wir vergleichen die vermutlich keineswegs zufälligen Ergebnisse unseres Schützen mit einem völlig zufälligen Schießen, allerdings unter der Vorgabe p = 0,9.)

Diesen Bereich nennen wir auch "Annahmebereich", und im vorliegenden Fall heißt das: wenn der Schütze zwischen 8 und 10 mal trifft, glauben wir ihm, dass er üblicherweise mit der Wahrscheinlichkeit p = 0,9 trifft, dass er also tatsächlich ein so guter Schütze ist, wie er behauptet.

Komplementär dazu reicht der "Ablehnungbereich" hier von 0 (= gar keinem) Treffer bis 7 Treffer: wenn der Schütze also zwischen 0 und 7 mal trifft, glauben wir es ihm nicht, dass er üblicherweise mit der Wahrscheinlichkeit p = 0,9 trifft, und unterstellen ihm, dass er ein Angeber ist.

Nun stellt sich aber die Frage, wie breit unser Annahmebereich sein sollte, um

• dem guten Schützen, der nur mal "einen schlechten Tag hat", trotzdem eine faire Chance zu lassen,
• gleichzeitig aber einen wirklich grottenschlechten Angeber zu entlarven

(wobei - zum wiederholten Mal gesagt - natürlich die Unwägbarkeiten bleiben, dass

• der wirklich gute Schütze beim Probeschießen aufgrund widriger Umstände kaum oder sogar gar nicht trifft,
• der Angeber beim Probeschießen versehentlich sehr häufig oder sogar jedes Mal trifft).

Wie gesagt: es geht um faire Chancen, aber wir können Fehleinschätzungen nicht völlig ausschließen.

Was aber heißt "faire Chance", und das bedeutet eben auch: gibt es ein mathematisches Maß für diese "faire Chance"?

Hier kommen wir aber, wenn die Rechnungen halbwegs einfach sein sollen, nicht weiter, und deshalb kommen wir zu

2. konkreter, d.h. Binomialteil:

Wohlgemerkt:

• alles bislang Gesagte gilt (hoffentlich!) für alle Wahrscheinlichkeitsverteilungen,
• das meiste Folgende hingegen nur für den Spezialfall "Binomialverteilungen".

Hier sei vorweg auf das Vorwissen über Binomialverteilungen aus

verwiesen.

Das betrifft insbesondere

1. das Aussehen der Graphen solcher Binomialverteilungen,
2. die Bestimmung (nur beim Spezialfall "Binomialverteilungen"!)

• des Erwartungswerts als μ  = n • p,
• der Varianz als σ² = n • p •  (1 - p) =

                  =   μ    •  (1 - p) ,

• der Standardabweichung als σ , also der Wurzel aus der Varianz.

Diese Rechenverfahren sind auch in   nicht hergeleitet worden, d.h. man musste sie einfach "glauben".

(Nun ließen sich die Regeln ja im Unterricht durchaus herleiten, es scheint mir nur fraglich, ob das zumindest in einem Mathe-Grundkurs sinnvoll ist - und ob man da nicht besser die anschaulichen Folgen behandelt.)

Und damit komme ich zu "mathematischer Theologie":

(nur) für Binomialverteilungen gibt es einige sogenannte "Sigma-Regeln"

(von σ = Standardabweichung):

Diese Sigma-Regeln muss man "einfach nur glauben". Sie kommen zwar in allen Schulbüchern, die ich zu Rate gezogen habe, vor, werden dort aber nie bewiesen, so dass mir fast schien, dass sie sich gar nicht beweisen lassen, sondern nur Erfahrungswerte sind. Stimmt aber nicht, sondern sie lassen sich durchaus beweisen, wenn auch nur mit fortgeschrittenen Mitteln (vgl. etwa ).

Zudem kann man sich die umständlichen Sigma-Regeln

(z.B. )

wohl kaum merken, sondern die schlägt man in Formelsammlungen nach.

Des weiteren ist zu klären, was beispielsweise der Formelsalat eigentlich bedeutet:

• die "1σ-Regel" besagt, dass die Anfangshypothese mit der Wahrscheinlichkeit P ≈ 0,68 (entspricht 68 %) richtig ist, wenn das Versuchsergebnis im Anahmebereich [ μ  - 1 • σ ; μ  + 1 • σ ] liegt. Anhand einer vorerst beliebigen Wahrscheinlichkeitsverteilung ergibt das graphisch folgenden Annahmebereich (und Ablehnungsbereich):

• entsprechend ergibt sich nach der "2σ-Regel" eine ca. 95,5-%-ige Sicherheit im Annahmebereich [ μ  - 2 • σ ; μ  + 2 • σ ]

• und nach der "3σ-Regel" ergibt sich eine ca. 99,7-%-ige Sicherheit im Annahmebereich [ μ  - 3 • σ ; μ  + 3 • σ ]

Dabei wird schon deutlicher: je breiter der Annahmebereich, desto eher fallen Werte hinein, desto sicherer kann ich mir meines Urteils also auch sein.

Die Frage, welche Sicherheit ich verlange, hängt teilweise von meiner Risikobereitschaft ab, ist also subjektiv; und sie richtet sich nach dem Anlass: beispielsweise

• bei Umfragen verlangt man oftmals eine 95-%-ige Sicherheit,
• bei der stichprobenartigen Erprobung von Medikamenten verlangt man hingegen oftmals eine 99-%-ige Sicherheit.

Die entsprechenden Radien der Annahmebereiche entnimmt man dabei folgender Tabelle:

Allemal erstaunlich finde ich aber die in der Mathematik doch ganz ungewöhnliche

(fast schon "theologische")

 Schwammigkeit von

:

1. kommen da drei Ungefähr-Zeichen vor,
2. ist "[d]iese Näherung [...] um so besser, je größer n ist"

(auf unser Probeschießen bezogen: je häufiger in ihm geschossen wird, desto weniger spielt beim Angeber der Glücksfaktor und beim Könner die Tagesform eine Rolle [Gesetz der großen Zahlen], desto sicherer können wir uns also unseres Urteils sein):

wie groß aber muss n denn sein? 

3. "In der Regel verlangt man σ > 3": wieso? Und was ist, wenn σ in der Nähe von 3 liegt?

Werden wir damit aber konkret und kommen zu unserem Probeschießen-Beispiel unter der Hypothese p = 0,9 zurück. Es ergibt sich:

• μ = n • p = 10 • 0,9 = 9,
• σ² = μ • (1 - p)        = 9 • (1 - 0,9) = 9 • 0,1 = 0,9
• σ  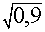=                                                                 ≈  0,94 .

                  [ μ  - 1 •    σ   ; μ  + 1 •   σ    ] =

=[ 9  - 1 • 0,94 ; 9  + 1 • 0,94 ] :

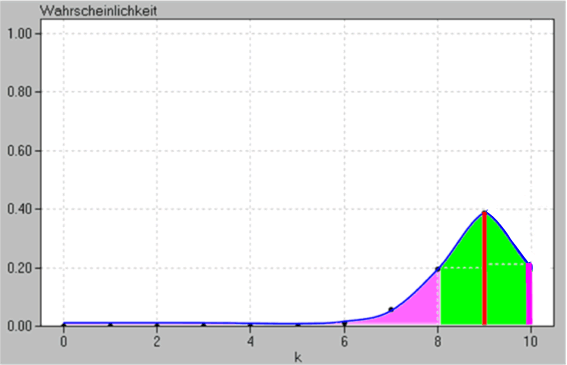
Die einzige ganze Zahl, die in diesem Annahmebereich liegt, ist die 9, so dass wir die Hypothese nur dann beibehalten, wenn der Schütze 9 mal trifft, d.h. wir halten ihn dann für einen Könner. In jedem anderen Fall, also

1. bei 0 bis 8 Treffern,
2. aber auch bei 10 Treffern,

verwerfen wir unsere Anfangshypothese p = 0,9 und halten den Schützen für einen Angeber.

Nun ist aber der Fall b. offensichtlich Blödsinn, denn dann hielten wir ja auch jemanden, der immer trifft, für einen Angeber.

Wie konnte solch ein Blödsinn aber passieren?:

1. wohl, weil n = 10 zu klein ist,
2. und auch als Folge aus 1., weil σ  ≈  0,94 zu klein, nämlich erheblich kleiner als 3 ist.

Spätestens hier wird es Zeit, eine kleine Änderung vorzunehmen:

es war von Anfang an wenig sinnvoll, für einen guten Schützen die punktuelle Wahrscheinlichkeit p = 0,9 anzunehmen. Vielmehr ist es sinnvoll, für die Wahrscheinlichkeit einen Bereich, nämlich z.B. 0,9 ≤ p ≤ 1 bzw. p ≥ 0,9, anzunehmen, denn schließlich würden 10 Treffer ja nur um so deutlicher das Können des guten Schützen herausstellen.

Deshalb nennen wir das Intervall [9; 10] "sicheren Annahmebereich", und wir kümmern uns nur noch um die Sigma-Abschätzung links davon. Wir führen also nicht mehr einen "beidseitigen", sondern nur noch einen "ein-", nämlich hier "linksseitigen" Hypothesentest durch:

Entsprechend ergibt sich für die Anfangshypothese, dass der Schütze ungeübt ist, nicht mehr beispielsweise p = 0,3,

• sondern 0 ≤ p ≤ 0,3 bzw. p ≤ 0,3,
• sicherer Annahmebereich [0; 3],
• rechts davon der Sigma-Bereich,
• also rechtsseitiger Hypothesentest.

---

Ein schönes Programm, mit dem man alle Möglichkeiten systematisch und kontinuierlich

(vgl. )

durchspielen kann, ist nebenbei

(Download) .

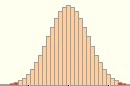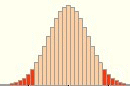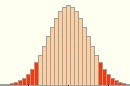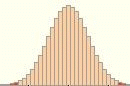
Dabei soll uns im Folgenden nur das Aussehen des Annahme- (hier hellblau) und Ablehnungsbereichs (hier dunkelblau) interessieren: 

• p wird sukzessive größer, n und der Sicherheitsanspruch bleiben hingegen unverändert:

 

• n wird sukzessive größer, während p und der Sicherheitsanspruch unverändert bleiben:

• der Sicherheitsanspruch wird sukzessive größer, während p und n unverändert bleiben:

(Nebenbei: mit dem Programm sind auch einseitige Hypothesentests darstellbar.)

Wenn wir nun beispielsweise die 1σ-Regel" anwenden, also sehr risikofreudig mit einer ca. 68-%-igen Sicherheit zufrieden sind, ergibt sich als Annahmebereich