innermathematische Veranschaulichung
(am Beispiel von Termumformungen)
Unter "Termen" versteht man in der Algebra alle Ausdrücke, dieIn diesem Sinne ist z.B. 3x2 oder 2x2 oder 3x2 -2x2 oder 4 ein Term, nicht aber 3x2 -2x2 = 4. Letzteres ist eine Gleichung, die aus den beiden Termen 3x2 - 2x2 links und 4 rechts besteht.
- aus Zahlen, Unbekannten (also Platzhaltern wie z.B. a, b oder x und y für noch unbekannte Zahlen), Rechenzeichen (incl. Wurzel, sin ...) sowie Klammern bestehen, aber
- KEIN Gleichheitszeichen enthalten.
Terme tauchen also oftmals in Gleichungen auf, und Gleichungen gilt es oftmals zu lösen (um herauszufinden, was für eine Zahl sich hinter einer Unbekannten wie z.B. x befindet). Der wichtigste Weg, Gleichungen zu lösen bzw. die Unbekannte zu finden, ist die sogenannte Termumformung (meist gleichbedeutend mit Termverkürzung bzw. –vereinfachung). Z.B. lässt sich der Term 3x2 – 2x2 zu (1)x2 vereinfachen, und dementsprechend wird aus der Gleichung 3x2 – 2x2 = 4 die einfachere Gleichung x2 = 4. Da aber kann man nun einfach ablesen, was hinter der Unbekannten x steht, nämlich entweder x = 2 oder x = -2.Termumformungen (und damit Gleichungslösen) sind nun aber unvermeidbar das A und O aller Mathematik, jede mathematische Anwendungsaufgabe läuft auf Terme bzw. Termvereinfachungen sowie Gleichungslösen hinaus. Gerade deshalb liegt es nahe, dass sich die Mathematiker das Prinzip selbst (eben die Termvereinfachung) vornehmen und erst mal von aller Anwendung absehen. Das ist ja gerade das Phantastische an der Mathematik, dass ein und dieselbe Gleichung(-sklasse) auf verschiedenste Anwendungen zutreffen kann und deshalb nicht immer neu (auf jeweils verschiedene Art) gelöst werden muss, sondern auf eine Art (nach einem Prinzip) gelöst werden kann. Die Schulmathematik hat daraus zwei Konsequenzen gezogen:
Die Wahrheit liegt vermutlich mal wieder in der banalen Mitte: die T & G nun völlig oder weitestgehend den Rechnern zu überlassen, scheint mir eben auch wieder gefährlich. Denn dann bleibt ein (nun mal) GRUNDHANDWERKSZEUG der Mathematik garantiert weitgehend unverstanden (weshalb soll ichs lernen bzw. nochmals rechnen, wenn ein Rechner es doch viel schneller kann?). Und was eigentlich ist, wenn der Rechner mal ausfällt – oder Quatsch rechnet? Denn mit oder ohne Rechner scheint mir das eigentliche Problem doch ganz woanders zu liegen, bzw. dieses Problem wird meiner Meinung nach in der derzeitigen Diskussion zumindest völlig unterschätzt oder verschwiegen:
(Wenn ich den Schnitt der SchülerInnen als so begriffsstutzig darstelle, dann nicht, weil ich - wie inzwischen wieder viele - meine, "die Jugend von heute" werde immer dümmer, sondern weil es mir letztlich um die Ursache für Begriffsstutzigkeit also [meinen] unanschaulichen Unterricht geht. Nebenbei: bei dieser konventionellen Mathepädagogik hat der Schnitt der SchülerInnen früher auch nicht mehr verstanden.)
Woran liegt es, dass die SchülerInnen mit rein inner(!)mathematischen Termumformungen und Gleichungslösen so große Schwierigkeiten haben? Nun, einerseits liegt es vielleicht (trotz ewig langer Behandlung der T & G?) an mangelnder Übung: so einiges Standardhandwerkszeug muss man nunmal in ewig langer, manchmal auch frustrierender Übung so zu beherrschen gelernt haben, dass man die Handgriffe geradezu unbewusst und mit links beherrscht. Z.B. über eine der berühmtesten Termumformungen, den 1. Binomi, also (a + b)2 = a2 + 2ab + b2, kann und darf man im Eifer des Gefechts (wenn ein Binomi in einer komplizierteren Rechnung nur noch Hilfsmittel ist) nicht mehr lange nachdenken, sondern er muss einem ins Blut übergegangen sein und automatisch (und dann fehlerfrei, also incl. des 2ab) abspulbar sein. Und doch kann solch mangelnde Übung eigentlich kein Grund für Probleme von SchülerInneN mit T & G sein: dazu werden sie gerade in der Mittelstufe allemal lange genug, ja, geradezu exzessiv lange durchgenommen. Fast könnte man sich da fragen, ob die ewig lange Behandlung geradezu kontraproduktiv ist. Der eigentliche Grund für die Schwierigkeiten von SchülerInnen mit Terumumformungen und Gleichungslösen scheint mir ganz woanders zu liegen:
| Termumformungen und Gleichungslösungen werden für SchülerInnen nie INNERmathematisch anschaulich. |
(Mir wird in der derzeitigen mathematik-pädagogischen Diskussion viel zu viel über [außermathematische] Anwendungen [und auch Computer, die allemal - alles zu seiner Zeit - ein geeignetes Hilfsmittel sein können], aber viel zu wenig über den eigentlichen Beruf des Mathematiklehrers, nämlich die INNERMATHEMATISCHE VERANSCHAULICHUNG, gesprochen!)Aber was soll das denn eigentlich sein, diese innermathematische Veranschaulichung, die ich ja offensichtlich von außermathematischen, also anwendungsorientierten Veranschaulichungen absetze? Schauen wir uns dazu die übliche Funktion von Anwendungsaufgaben im Mathematikunterricht an: für Mathematiker ist jede andere Wissenschaft/Anwendung nur eine Hilfswissenschaft mit dem einzigen Zweck, mit ihrer Hilfe innermathematisch Wichtiges zu veranschaulichen. Meistens sind die Anwendungs- bzw. Text-Aufgaben allerdings auch danach, d.h. von der Mathematik (dem gerade beizubringenden mathematischen Stoff) aus hochgerechnet und dementsprechend unrealistisch:
im Rahmen einer sogenannten landwirtschaftlichen Flurbereinigung sollen zwei quadratische äcker zu einem flächengleichen quadratischen Acker zusammengelegt werden.
Das ist offensichtlich der in Landwirtschaft verpackte Satz des Pythagoras, also
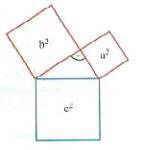
Nun, solche Aufgaben haben durchaus ihre Vorteile: die eigentliche Mathematik dahinter ist relativ einfach wiedererkennbar. So gesehen können die SchülerInnen sogar heilfroh sein, keine echten Anwendungsaufgaben zu bekommen, bei denen es teuflisch schwierig sein kann, die dahinter liegende (falls überhaupt eindeutig vorhandene) Mathematik herauszudestillieren. Solche Aufgaben haben aber auch zwei entscheidende Nachteile:
- so was kommt nichtmal in realistischer Flurbereinigung vor,
- und was haben SchülerInnen eigentlich mit Flurbereinigung (die letzte war vor ewigen Zeiten) am Hut?
(Wie schon angedeutet, ist es oftmals gar nicht einfach, solche Mathematik aus der Anwendungsaufgabe heraus zu destillieren.)Viel problematischer ist aber aus innermathematischer Sicht, dass die Anwendungsaufgabe rein gar nichts zur Veranschaulichung des Terms beiträgt, weil der Weg von der Anwendungsaufgabe zum Term viel zu lang ist, als dass er noch überschaut werden könnte. So oder so (seis innermathematisch, seis als Konsequenz aus einer außermathematischen Anwendungsaufgabe) müssen SchülerInnen aber nun mal mit solchen Termen hantieren können. Also bedarf es einer anderen, inner-mathematischen Veranschaulichung: wie kann man den Term 4x2 + 4x3 + 9x2 + 3x + 8x + 7x3 sowie den korrekten Umgang mit ihm veranschaulichen, ohne zu allzu weit entfernten äußeren Anwendungsaufgaben zu greifen? Und selbst mal angenommen, es gäbe eine Anwendungsaufgabe, die sehr nahe mit dem aus ihr resultierenden Term 4x2 + 4x3 + 9x2 + 3x + 8x + 7x3 zusammen hinge:
a 2 + b 2 = c 2
a Quadrat plus b Quadrat gleich c Quadrat
/ - - | _ | / - - | _ | / - -
(also ein Daktylus [ / - - ] bzw. ¾-Walzertakt!)
Bzw. man hört dann einfach, dass beim Binomi (a + b)2 = a2 + 2ab + b2 das sogenannte gemischte Glied, also 2ab, nicht wegfallen darf (der häufigste SchülerInnenfehler dabei).Worums mir hier am Beispiel der Termumformung geht, ist der entscheidende erste Schritt, also die innermathematische Veranschaulichung – und ihre bezeichnende Problematik. Mein Vorschlag: x3 als Würfel (räumliches Objekt), x2 als Quadrat (Fläche) und x als Strecke zu illustrieren. Natürlich ist auch das nicht puristisch innermathematisch, sondern hat mit gegebenen Dingen der Außenwelt zu tun – und ich würde es ja durchaus mit echten, anfassbaren Würfeln, Quadraten und Strecken illustrieren.
(Denn letztlich geht es ja - soweit irgend möglich - um echtes Be-GREIFEN!)Würfel, Quadrate und Strecken sind aber doch wieder nur geometrische Gegenstände, und die Geometrie ist wiederum ein Teilgebiet der Mathematik. Solche Veranschaulichung ist also höchstens außeralgebraisch, aber (weil geometrisch) nicht außer-, sondern innermathematisch. Mit Würfeln, Quadraten und Strecken veranschaulicht, sieht der Term
4 x2 + 4 x3 + 9 x2 + 3 x + 8 x + 7 x3
folgendermaßen aus:
4
+ 4
+ 9
+ 3 x + 8 x + 7
(*)
Und weil nun ja jeder weiß, dass man wohl (gleichgroße) Würfel zu Würfeln bzw. Quadrate zu Quadraten bzw. Strecken zu Strecken, diese drei Objektarten aber nicht untereinander addieren kann (was soll ein Würfel plus eine Strecke sein?), ergibt sich automatisch die Termumformung bzw. –vereinfachung
11
+ 13
+ 11 x ,
d.h. wird
(Ich hab all das mit mehren Laien [deren Schulzeit zwanzig Jahre her ist] ausprobiert. Und ich bin mächtig stolz drauf, dass ich die Probleme [**] und Fehler [***] haargenau vorausgesehen hatte [ja, sie mittels der Reihenfolge 4 x2 + 4 x3 fast schon hinterhältig überhaupt erst heraufbeschworen hatte], dass aber auch mein Veranschaulichungsansatz [*] alle Probleme sofort behob! Denn einE LehrerIn lernt ja überhaupt nur aus den typischen Fehlern seiner SchülerInnen!)Für meine gesamte Argumentation in diesem Text ENTSCHEIDEND ist aber:
| Innermathematische Veranschaulichungen haben also erst mal mit Anwendungen reichlich wenig zu tun, und deshalb ist es ein Denkfehler, man müsse nur Anwendungsaufgaben (die ja durchaus auch ihren anderen Sinn haben) geben, und schon verstünden die SchülerInnen alles (die Mathematik) besser. |
Innermathematische Veranschaulichung wird mir aber viel zu wenig betrieben, und DAS ist der Grund, weshalb viele SchülerInnen nichtmal Mathematik (geschweige denn mathematische Anwendungen) wirklich begreifen.
Der Versuch, z.B. x2 durch ![]() zu veranschaulichen, ist vielfach aufschlussreich:
zu veranschaulichen, ist vielfach aufschlussreich:
"Das indische Zahlensystem eignete sieh sehr gut für alltägliche Aufgaben wie Addieren und Multiplizieren, aber die Wirkung der indischen Zahlen war noch weitaus tiefgründiger. Die Zahlen hatten jetzt nicht mehr nur in der Geometrie eine Bedeutung und dienten nicht mehr nur dazu, die Abmessungen oder Anzahlen von Gegenständen anzugehen. Anders als die Griechen sahen die Inder in Quadratzahlen keine Quadrate und in Produkten zweier verschiedener Zahlen keine Rechtecke. Statt dessen erkannten sie das Wechselspiel von Zahlenzeichen - von Zahlen, die ihrer rein geometrischen Bedeutung entkleidet waren. Das war der Ursprung dessen, was wir heute Algebra nennen. Diese Einstellung verwehrte es den Indern zwar, wesentlich zur Geometrie beizutragen, hatte aber eine andere, unerwartete Konsequenz: Sie befreite sie vom den Beschränkungen der griechischen Denkweise - und von deren Ablehnung der Null. Sobald die Zahlen ihre rein geometrische Bedeutung verloren hatten, mussten sich die Mathematiker nicht mehr um den geometrischen Sinn der mathematischen Aktionen kümmern. Wir können zwar kein Feld mit drei Hektar von einem Feld mit zwei Hektar wegnehmen, aber nichts hindert uns, drei von zwei abzuziehen. Heute wissen wir, dass 2 - 3 = - 1 ist, also minus eins ergibt. Im Altertum und im Mittelalter war das jedoch keineswegs einleuchtend. Oft löste man Gleichungen, erhielt ein negatives Ergebnis und schloss daraus, die Lösung habe keine Bedeutung. Was soll denn auch für jemanden, der in rein geometrischen Begriffen denkt, eine negative Fläche bedeuten? Sie ergab für die Griechen einfach keinen Sinn. Die negativen Zahlen waren für die Inder durchaus sinnvoll und traten tatsächlich erstmals in Indien (und in China) auf." (Charles Seife)
Aber stimmt es eigentlich wirklich, dass die Vorstellung völlig weg-abstrahiert wurde?:
Bei der Untersuchung der Hirnleistung rechnender Menschen fanden Forscher [...] ihre Vermutung über das Arbeitsgedächtnis bestätigt. Bei allen Probanden leistete es Schwerstarbeit. Das galt besonders für jenen [Gehirn-]Bereich, der sich mit der Zwischenspeicherung räumlich-visueller Informationen beschäftigt; Hirnforscher nennen ihn den »räumlich-visuellen Notizblock«. Dieser Befund ist insofern bemerkenswert, als Zahlen an sich keine räumlich-visuelle Qualität haben. Eine Neuronengruppe, die gewöhnlich immer dann aktiv wird, wenn wir unsere Finger bewegen, lief ebenfalls heiß. Offensichtlich hinterlässt die frühkindliche Art des Zählens und Rechnens Spuren im Gehirn: Die gleichen Neuronen, die damals beansprucht wurden, beteiligen sich auch an den Rechenleistungen der Erwachsenen.
[...]
Nach eigenem Bekunden strukturiert er [ein sogenannter Rechenkünstler] den Dschungel der Zahlenwelt mit Hilfe visueller Vorstellungen."
(Spektrum der Wissenschaft, 6/2001, S. 16f)Es ist wie mit dem Leise-Lesen: In einer anderen Untersuchung scheinen Wissenschaftler herausgefunden zu haben, dass dabei im Gehirn durchaus die meisten motorischen Regionen angeschaltet werden, die man zum (Laut-)Sprechen braucht, und erst ganz am Ende erfolgt der Befehl "doch nicht aussprechen".
Bauen sich Menschen letztlich nicht eben doch (neue) Bilder?:
Beispielsweise ein Quantenphysiker wie Niels Bohr, der immer wieder darauf bestanden hat, dass die Quantentheorie "gehirnausrenkend" sei und (auch und gerade ihm selbst) unanschaulich-unverständlich, muss dennoch irgendwelche "Bilder" für sie gehabt haben - und hat dementsprechend auch das (ebenso erkenntnisfördernde wie -behindernde) bohrsche Atommodell entwickelt:
![]()
Ein weiteres Beispiel:
Bei der Erkundung mehrfacher Nullstellen kubischer Funktionen liegt es natürlich nahe, das auch graphisch zu tun:
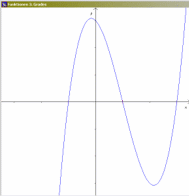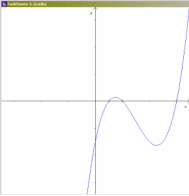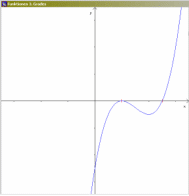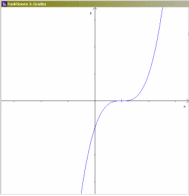
© Robert Hohm
Um aber eindrücklich zu "kapieren", was da passiert, scheint mir noch mehr nötig:
ein "inneres" Bild, das den doch ziemlich abstrakten Vorgang visualisiert, der da passiert. Schauen wir uns dazu nochmals an, was
im ersten Teil der oben gezeigten Animation passiert:
die linke Nullstelle wandert gegen die mittlere, und dabei wird der linke "Berg" (zwischen linker und mittlerer Nullstelle) immer kleiner, bis die mittlere Nullstelle eine doppelte Nullstelle wird (ein Berührpunkt).
Nehmen wir nun das Bild des Berges mal wörtlich - und ergänzen, dass die x-Achse der Meeresspiegel ist:
da versinkt ein Berg im Meer (wird immer kleiner bis hin zu einem Hügel, einer Sandbank usw.) - und urplötzlich ist er ganz abgetaucht, berührt aber noch gerade den Meeresspiegel von unten.
entsprechend kann man sich auch den zweiten Teil der Animation erklären:
jetzt wandert auch noch die rechte Nullstelle gegen die mittlere, und dabei wird das rechte "Tal" (zwischen rechter und mittlerer Nullstelle) immer höher, bis die mittlere Nullstelle eine dreifache Nullstelle wird (ein Sattelpunkt).
Nehmen wir nun auch hier das Bild, in diesem Fall also das Tal, wieder wörtlich:
da steigt ein Tal langsam aus dem Meer empor (wird immer weniger tief und breit bis hin zu einem Fluss, einem Rinnsal usw.) - und urplötzlich berührt es gerade eben den Meeresspiegel von unten.Das entsprechende Bild wäre hier das Auftauchen neuer Inseln aus dem Meer.
Das Bild (ein ins Meer absinkender Berg bzw. ein aufsteigendes Tal) ist keinerlei "Anwendung" und hat natürlich rein gar nichts mit der mathematischen Sache zu tun - und veranschaulicht sie dennoch wunderbar.
Ein "Sattelpunkt" (diese ja nicht zwecklos gewählte mathematische Metapher) ist dann tatsächlich ein Sattelpunkt
,
also der Punkt eines Pferderückens, an dem der Reiter sicher sitzt (an dem die Tangente waagerecht ist).
Auch und gerade Mathematik erfährt (!) man erst richtig in einer Art (mystischen) "Schau", d.h. in einem Zusammensehen von Konzepten und Strukturen in inneren Bildern:
"Du aber, lieber Timotheus, wenn Du Dich um die mystische Schau strebend bemühst, verlaß die sinnliche Wahrnehmung und die Denktätigkeit, alle Sinnendinge und Denkinhalte, alles Nicht-Seiende und Seiende, und strebe erkenntnislos zum Geeintwerden - soweit dies möglich ist - mit dem über allem Sein und Erkennen Liegenden empor. Denn durch das von allem Gehaltenwerden freie und rein von allem gelöste Heraustreten («Ekstase») aus Dir selbst wirst Du, alles von Dir abtuend und von allem gelöst, zum überwesentlichen Strahl des göttlichen Dunkels emporgehoben werden."
(Dionysius Areopagita: Von der mystischen Theologie)