∫
 (oder das Drama der Erkenntnis)

Ich werde hier nicht die Differential- und Integralrechnung erklären.

Nur so viel:

• beide befassen sich (in der Schulmathematik) mit krummlinigen Funktionsgraphen

... wofür die Normalparabel, also der Funktionsgraph der quadratischen

(also sozusagen ersten nicht-linearen)

Funktion f: y = x² das einfachste, aber doch ein hinreichend aussagekräftiges Beispiel ist:

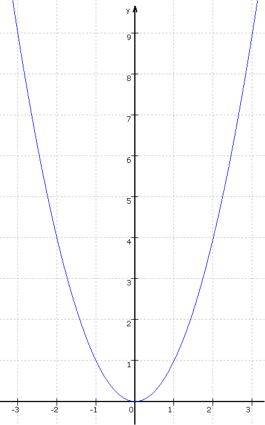
Die Probleme ergeben sich gleich, wenn man an diesen Funktionsgraphen Standardfragen stellt, die

• bei linearen Funktionen

• und überhaupt in der üblichen Schulgeometrie

(außer bei Kreisen)

sehr leicht zu beantworten sind:

1. wie groß ist die Steigung?

(Bei einer linearen Funktion mit der Funktionsgleichung f: y = mx + b ist eben m die Steigung;
 oder man kann die Steigung auch leicht am Graphen ablesen: 1 nach rechts, m nach oben bzw. unten.)

2. wie groß ist die Fläche unter dem Graphen?

(Bei einer linearen Funktion ist das eine Dreiecks-, also die Hälfte einer leicht zu berechnenden Rechtecksfläche.)

(Hier sei mal nicht gefragt, warum man überhaupt solche "Standardfragen" stellt.)

• Schauen wir uns zuerst 1., also die Steigungs-Berechnung an:

dabei ergibt sich das gravierende Problem, dass die Normalparabel

• nicht mehr

(wie noch lineare Funktionen)

immer dieselbe Steigung hat,

• sondern (rechts der y-Achse, also für positive x) immer stärker (von Punkt zu Punkt) steigt, so dass

  • in jedem der unendlich vielen, nah beieinander liegenden Punkte (also beispielsweise o oder o) eine andere Steigung vorliegt,

  • insgesamt also unendlich viele Steigungen vorliegen:

• Im Grunde dasselbe Problem ergibt sich, wenn man eine Fläche unter der Normalparabel berechnen will:

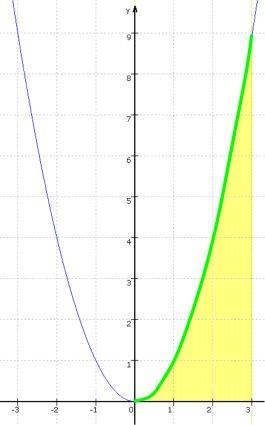
Weil die "Oberkante" der Fläche, also der Ausschnitt der Parabel, nicht gerade, sondern krumm ist, hilft hier nicht mehr

(zumindest nicht auf Anhieb)

die einfache Flächenberechnung mittels Dreieck/Rechteck, die noch bei linearen Funktionen schnell zum Ziel führte.

Und hier nun beginnt sozusagen "des Dramas erster Teil" :

1. ist es doch wohl bemerkenswert, dass man das scheinbar unlösbare Problem

(eben z.B.  "unendlich viele Steigungen")

doch lösen kann

(und das haben vor allem Newton und Leibniz geschafft):

1. zur Steigung:

   • man nähert die "endgültige" Tangente --- in einem Punkt o

_{(deren Steigung dann auch die Steigung der Parabel in diesem Punkt ist)}

mittels Geraden ······ an, die durch zwei Punkte (o und einen anderen Punkt o) gehen und daher mit Hilfe der "Zweipunkteform" der Geradengleichung leicht zu berechnen sind:

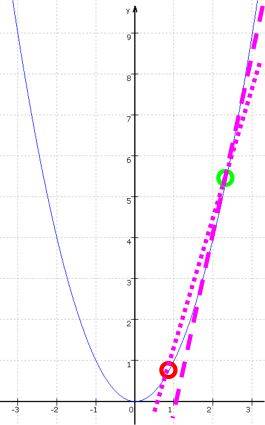
Bemerkenswert daran ist die Kombination zweier genialer (genial einfacher?) Kunstgriffe:

1. dass man einfach das tut, was man bereits kann, nämlich mit Geraden hantieren,

2. die unendliche Annäherung (Limes) des roten Punktes an den grünen Punkt;

• rechnerisch führt das

(was hier nicht genauer erklärt werden soll)

zu folgendem Verfahren:

1. die "Ableitung" (das "Differential") von f(x) = x² ist erstaunlich einfach zu erhalten, indem man die 2 vor das x zieht

(und den Exponenten um 1 von 2 auf 1 verringert),

ergibt sich also als f (x) = 2x;

2. wenn ich nun die Steigung beispielsweise im Punkt P(3|9) wissen will, setze ich einfach die 3 für x in f (x) ein und erhalte als Steigung 2 • 3 = 6

(und so erhalte ich analog für jeden Punkt Q(x|y) die ganz eigene Steigung in diesem Punkt; oder anders gesagt: f (x) = 2x ist - gar nicht so selbstverständlich! - wieder eine hübsche und zudem einfachere, nämlich lineare Funktion, die jedem Punkt Q kontinuierlich die Steigung in eben diesem Punkt zuordnet.)

2. zur Flächenberechnung:

• ich finde es doch höchst erstaunlich und damit auch dramatisch, dass hier glücklicherweise fast dasselbe Verfahren wie bei der Steigungsberechnung zum Ziel führt:

1. dass man einfach das tut, was man bereits kann, nämlich mit Rechtecken

(statt - wie bei der Steigung noch - Geraden)

hantieren,

2. die unendliche Annäherung (Limes) durch zunehmend schmalere Rechtecke:

• und auch das Rechenverfahren ist wieder sehr einfach:

arg fachsprachlich geschludert:

1. das "Integral" von f(x) = x² ist erstaunlich einfach zu erhalten, nämlich F(x) = x ³

(die 3 kommt dabei durch 2 + 1 zustande);

2. wenn ich nun die Fläche unter der Parabel bis zum Punkt P(3|9) wissen will, setze ich einfach die 3 für x in F(x) ein und erhalte als Fläche  ● 3³ = ● 27 = 9

(und so erhalte ich analog für jeden Punkt Q(x|y) die ganz eigene zugehörige Fläche bis dorthin; oder anders gesagt: F(x) = x ³ ist - gar nicht so selbstverständlich! - wieder eine hübsche, wenn auch diesmal kompliziertere Funktion [3. Grades], die jedem Punkt Q kontinuierlich die zugehörige Fläche bis zu eben diesem Punkt zuordnet.)

2. Obwohl doch

• einerseits die Ableitung (Steigung in einem Punkt)

• und andererseits die Integration (Fläche bis zu einem Punkt)

von ganz Unterschiedlichem handeln, hängen sie erstaunlicherweise über den

"Hauptsatz der Differential- und Integralrechnung"
(also einen der dramatischen Gipfel der gesamten Mathematik!)

doch eng zusammen, wie sich oben mit der hellblauen Einfärbung andeutete:

wenn ich

• f(x) = x² integriere, erhalte ich als Ergebnis F(x) = x ³,

• und wenn ich nun F(x) wieder ableite, erhalte ich F (x) = x²,

• also wieder f(x).

Ableitung und Integration sind also das glatte Gegenteil voneinander bzw. stehen in wechselseitiger Verbindung miteinander.

Wie so oft, kommt das rechnerisch (mit einem lauten Knall!) einfach raus - und bleibt doch unanschaulich.

Denn was - bittschön - hat

• die Steigung in einem einzigen Punkt

• mit der Fläche bis dorthin

zu tun, wo sich doch die Fläche durch alle Oberkantenpunkte bis dahin definiert?

Erste, wenn auch kaum anschaulichere Lösungsansätze für dieses Problem:

• in die Fläche gehen alle Oberkantenpunkte ein, in denen jeweils spezifische Steigungen vorliegen;

• alles wird zusammengehalten durch die Ausgangsfunktion f: y = x², die "stetig", also mit einem einzigen durchgezogenen Strich gezeichnet werden kann; man kann sich diese Funktion fast wie eine spezifisch gespannte Kunststoffleiste vorstellen, deren Biegung

  • gleichermaßen in die Steigung

  • wie auch in die Fläche

  eingeht.

Damit aber zu "des Dramas zweitem Teil"  bzw. meinem ganz eigenen "Drama", das hier für mich überhaupt Schreibanlass ist.

1. Schon immer habe ich mich gefragt, warum (zumindest im Schulunterricht) andauernd

• die Steigung eines Funktionsgraphen

• und die Fläche unter ihm berechnet wird,

• aber nie die Bogenlänge in

.

Gibt es keine irgendwie sinnvolle Bedeutung (vgl. 2.) dieser Bogenlänge - oder ist ihre Berechnung für die Schule einfach zu schwierig?

(Denn natürlich habe ich mich auch gefragt, wie diese Bogenlänge denn zu berechnen wäre; vgl. ).

Zwar finde ich

"Die Berechnung der Bogenlänge ist für die Bearbeitung innermathematischer und vieler technischer (insbesondere bautechnischer) Probleme bedeutsam. Als Beispiele seien die Berechnung der Länge eines Parabelbogens, der Kettenlinie, einer Schleife oder eines Brückenbogens genannt."
(zitiert nach ),

aber leider bleibt da gerade der Teil, der mich am meisten interessiert, nämlich "für die Bearbeitung [welcher?]  innermathematischer [...] Probleme", arg allgemein.

(Für bessere Tipps bzgl. einer eventuellen "Bedeutung" der Bogenlänge wäre ich allemal dankbar!)

2. Für die Steigung bzw. Ableitung gibt es eine ganz einfache physikalische Bedeutung, nämlich die (Momentan-)Geschwindigkeit beim freien Fall

(und die zweite Ableitung ergibt dann die Beschleunigung; woher wusste die Natur das bzw. warum hat sie sich danach gerichtet?).

Da frage ich mich doch seit Langem, ob das Integral auch so eine hübsche physikalische Anwendung hat (und gar beim freien Fall)?

Zwar bin ich fündig geworden bei

"[...] die Arbeit [kann] als Fläche unter der Bedeutung der Kraft verstanden werden [...]"
(zitiert nach ),

was aber für mich als Nichtphysiker auch nicht gerade sonderlich anschaulich bzw. ergiebig ist.

(Auch hier wäre ich für anschauliche[re] Tipps dankbar!)

Man wird bemerkt haben, dass all das ein unbefriedigendes "Stochern im Ungefähren" ist.

Seit Langem geistert mir aber im Kopf herum, dass ich mal was Wichtiges über die "Bedeutung" des Integrals gewusst, es aber inzwischen (leider!) wieder vergessen habe. D.h. also, ich weiß nicht mal mehr, was ich (tatsächlich oder angeblich) mal gewusst habe.

Aber es hat mich nicht mehr in Ruhe gelassen!

Gestern aber, bei der Lektüre des Buches von Arthur Zajonc

(vgl. Bücher des Monats 10/06)

hatte ich plötzlich ein déjà-vu-Erlebnis mit aller solchen Erlebnissen eigenen eindrücklichen Macht, ja es war wieder mal, als wenn alle  bisherige Halbkenntnisse urplötzlich zu einem zentralen Punkt implodierten.

In den genannten Buch stand nämlich:

"Im Gegensatz zu den «differentialen» Gesetzen der Physik, die angeben, welche Kräfte von Augenblick zu Augenblick auf das Teilchen einwirken, während es sich bewegt, scheint sich das Prinzip der kleinsten Wirkung auf den gesamten, ungeteilten Weg zu beziehen. Formal kann man immer vom Integral zum Differentialverfahren übergehen, doch in jedem ist ein bestimmte Einstellung zur Welt beschlossen. Im differentiale Vorgehen sind wir der Baustellenleiter, der die Handwerke und die verwendeten Materialien beaufsichtigt; dann sind wir nur mit den notwendigen Ursachen befaßt. Doch wir könne auch einen Schritt zurücktreten [= integrieren] und das Werk bewundern, bevor es vollendet ist, und das Ganze vor unserem geistige Auge sehen. Dann können wir uns andere Entwürfe, andere gangbare Wege vorstellen, um den besten auszuwählen und eine göttliche Ursache zu erkennen. Beide Arten, die Aufgab zu betrachten, haben ihre Berechtigung.
[...]
Wir leben in der Schwebe zwischen dem Teil und dem Ganzen , dem Differential und dem Integral [...]"
(Hervorhebungen von mir, H.St.)

Vor lauter Betriebsblindheit benutzt man viel zu viele Wörter, deren (Hinter-)Sinn und Geschichte (Ethymologie) man nicht kennt, z.B.

• Mathematik: [...]  wurde im 15. Jh. aus [...] lat. (ars) mathematica entlehnt, das seinerseits aus griech. mathematike (téchne) übernommen ist. Das zugrundeliegende Adjektiv griech. mathematikós »lernbegierig; wissenschaftlich; mathematisch« ist von griech. máthema "das Gelernte, die Kenntnis" abgeleitet [...]. Stammwort ist griech. manthánein (Aorist: mathein) »[kennen]lernen, erfahren« [...]
  (Duden)

• in|te|g|ral (ein Ganzes ausmachend; vollständig; für sich bestehend)
  (Duden)

Das Integral ist also sozusagen das "Ganze", zusammengesetzt aus

• der Grundseite, über der die Fläche gemessen wird,

• allen (!) einzelnen (!) Punkten (samt den Steigungen in ihnen)

• sowie der Höhe des Graphen über der Grundseite,

während die Steigung immer nur einen einzelnen Punkt betrifft.

Und das ist ja geradezu auch anschaulich klar: die Steigung ist nur ein-, das Integral hingegen zweidimensional.

Eine der gigantischsten "Veranschaulichungen" (?) dieser Bedeutung von "Integral" ist das sogenannte "Feynman-" oder auch "Pfad-Integral":

"Viele Wissenschaftler halten [die Pfadintegralmethode] für die schönste Formulierung der Quantenphysik. Ihr zufolge [fliegt ein Quantenteilchen nicht einfach von A nach B, sondern] werden alle [!] Wege von einem Quantenteilchen, gleichgültig ob Licht oder Materie, zurückgelegt. Wenn man die zahllosen Wege zusammenfasst, kristallisiert sich einer [!; nämlich der von A nach B] heraus, dessen Wirkung am kleinsten ist."
[... wobei die Verbindung zwischen A und B nicht immer gerade sein muss; vgl. etwa die Ablenkung von Licht durch eine große Masse oder die Brechung beim Übergang von Luft in Wasser.]
(ebenfalls nach Arthur Zajonc zitiert).

Und doch bleibt ein schaler Nachgeschmack: "das Ganze" ist - auch in der Mathematik - ein bisschen arg viel und verleitet zu "Schwiemeligkeit": man kann froh sein, wenn man ein bisschen erahnt,

• wie sich das Ganze aus seinen Teilen zusammensetzt (das Ganze als Summe seiner Teile),

• wie z.B. zwei (von vielen) Teil-Komponenten zusammen mehr ergeben als ihre bloße Summe.