
hochtrabende Wörter, wichtiger Inhalt: Invarianz & Dualität

Jean Victor Poncelet
(1788 - 1867)
"Im Vorwort zu seinem klassischen Werk »Applications d'analyse et de géométrie« (1822) schildert Poncelet seine Erlebnisse auf dem katastrophalen Rückzug aus Moskau. Am 18. November 1812 wurden die erschöpften Reste der französischen Armee unter Marschall Ney bei Krasnoi überwältigt. Unter denen, die auf dem gefrorenen Schlachtfeld liegen blieben, war der junge Poncelet. Seine Uniform als Pionieroffizier rettete ihm das Leben. Ein Suchtrupp entdeckte, daß er noch atmete, und brachte ihn zum Verhör vor den russischen Stab.
Als Kriegsgefangener war der junge Offizier gezwungen, fast fünf Monate in den Fetzen seiner Uniform mit spärlichen Rationen von Schwarzbrot über die gefrorene Ebene zu marschieren. In einer so bitteren Kälte, daß häufig das Quecksilber im Thermometer einfror, kamen unterwegs viele von Poncelets Kameraden elend um, doch seine robustere Veranlagung ließ ihn das Ziel, das Gefängnis von Saratow an den Ufern der Wolga, erreichen. Zunächst war er zu erschöpft, um nachzudenken. Doch als ihn die »herrliche Aprilsonne« wieder zum Leben erweckte, erinnerte er sich daran, daß er eine gute mathematische Ausbildung genossen hatte; um sein hartes Los in der Verbannung zu erleichtern, beschloß er, sich so viel von dem Gelernten wie möglich ins Gedächtnis zu rufen. [...]
Ohne Bücher und anfänglich ohne den kleinsten Fetzen Papier spürte er allem nach, was er über die Mathematik, von der Arithmetik angefangen über die höhere Geometrie bis zur Infinitesimalrechnung, gewußt hatte. Diese ersten Versuche wurden durch Poncelets Bemühungen belebt, seine Mitgefangenen für die Prüfungen vorzubereiten, falls sie je Frankreich wiedersehen sollten. Zunächst hatte Poncelet nur ein Stück Kohle aus dem armseligen Becken, das ihn vor dem Erfrieren bewahrte, um seine Diagramme an die Wände des Gefängnisses zu zeichnen. Dabei machte er die interessante Feststellung, daß sich fast alle Einzelheiten und komplizierten Ableitungen der Mathematik verflüchtigt hatten und ihm nur die allgemeinen grundlegenden Prinzipien im Gedächtnis geblieben waren."
(zitiert nach: E. T. Bell: "Die großen Mathematiker)(Um vorweg den erahnbaren Einwand
"ja war der eigentlich bescheuert, dass der sich in solcher Not ausgerechnet mit Mathematik beschäftigt hat"
zu entkräften:
muss sich ein Mensch vielleicht gerade in solcher Not an irgendwas [Geistigem] festhalten - warum also nicht an der Mathematik?
gibt´s erheblich dämlichere Möglichkeiten als Mathematik.)
Und aus der typischen "Not" im fettgedruckten Satz
(An welche mathematischen Details erinnert sich denn jemand noch zehn Jahre nach dem Abitur, der nicht gerade Mathematik, Natur- oder Ingenieurswissenschaft studiert hat? Was von der Schulmathematik "braucht" man also "im Leben" - und auch in einem späteren Mathematikstudium?)
hat Poncelet eine Tugend gemacht, nämlich mangels genauerer Erinnerungen und Schreibmaterials an Grundsätzlicheres gedacht, und zwar an "Invarianzen":
Invariante [lateinisch »Unveränderliche«], Mathematik, Physik: eine für eine gegebene Klasse mathematischer (Zahl, Funktion, Vektor, Gruppe) oder physikalischer Objekte definierte Größe oder Eigenschaft, die sich bei Abbildungen, Symmetrieoperationen oder Transformationen nicht ändert; so sind z.B. die Längen und Winkel Invarianten in Bezug auf die Kongruenzabbildungen. Die Eigenschaft der Unveränderlichkeit von Größen (Invarianz) ist v.a. in der Physik von Bedeutung, da aus bestimmten Symmetrien auf Erhaltungssätze oder -größen (z.B. Energie, Drehimpuls) geschlossen werden kann.
(Brockhaus multimedial 2002)
Für einen Laien daran verständlich ist - wenn überhaupt zwischen all dem Fachchinesisch - nur:
"Größe oder Eigenschaft, die sich bei [bestimmten Tätigkeiten] NICHT äNDERT",
dass der ganze mathematische Invarianz-"Krempel" irgendwie auch eine ANWENDUNG (u.a. in der Physik) hat
(um die es im Folgenden nicht gehen soll).
Was da bei Poncelet passiert ist, rechne ich mir brachial auf die Schulmathematik runter:
"ich weiß zwar nicht mehr genau, wie man den Scheitelpunkt von quadratischen Funktionen der Form y = ax2+bx+c berechnet (und das lässt sich auch prima in Formelsammlungen nachschlagen), aber ich weiß noch, dass all ihre Graphen Parabeln sind und deshalb immer einen Scheitelpunkt haben;
d.h. Form und Scheitelpunktexistenz sind »invariant« gegenüber den Formvariablen a, b und c bzw. in »normalem« Deutsch: für die Form und die Scheitelpunktexistenz sind a, b und c herzhaft egal";
(um das klar zu machen, würde ich auch die Funktionenschar y = ax2+bx+c als eine, sich mit den kontinuierlich verändernden Formvariablen a, b und c kontinuierliche verändernde, aber immer Parabel bleibende Funktion ansehen)
"entsprechend ist y = ax2+bx+c auch bzgl. des sich kontinuierlich verändernden x invariant; ich kann alle/unendlich viele x einsetzen, wodurch sich jeweils ein Spezialfall ergibt, der ganze Krempel aber eine Parabel bleibt";
"ich weiß zwar nicht mehr genau, wie man geometrisch korrekt dreht, spiegelt und verschiebt, aber ich habe was ganz Alltägliches begriffen: man kann eine Figur solange drehen, spiegeln und verschieben, wie man lustig ist, sie ändert nie ihre Form, sondern nur ihre Lage: das wäre ja noch schöner, wenn beispielsweise die Form (Größe) eines Goldklumpens sich allein dadurch ändern würde, dass ich ihn ein wenig durchs Zimmer trage;
d.h. die Form (nicht jedoch die Lage) ist »invariant«bzgl. Drehung, Spiegelung und Scherung" (vgl. auch ![]() ).
).
"keine Ahnung, wie man Ähnlichkeitsabbildungen konstruiert (zentrische Streckung), aber ich weiß, dass sich bei ihnen wie auf einem Kopierer wohl die Größe verändert, nicht aber die Form (die also bzgl. der zentrischen Streckung »invariant« ist); bzw. dass sich wohl (im Gegensatz zu Kongruenzabbildungen) die Details, nicht aber (schon auf höherer Abstraktionsstufe) deren Beziehungen zueinander verändern";
"der »Binomi« (a + b)2 = a2 + 2ab + b2 ist »invariant« bzgl. der Wahl von a und b, d.h. er gilt für jede Wahl von a und b; oder allgemeiner gesagt: sämtliche Rechengesetze sind »invariant« gegenüber konkreten Werten";
"der Satz des Pythagoras a2 + b2 = c2 gilt für alle rechtwinkligen Dreiecke, ist also »invariant« gegenüber der konkreten Wahl von a, b und c; und die Winkelsumme 1800 ist sogar noch »invarianter«, gilt nämlich nicht nur (wie der Satz des Pythagoras) für rechtwinklige, sondern für sämtliche [ebenen] Dreiecke"
"eine (Zwölf-Stunden-)Uhr ist »invariant« gegenüber jedem Weiterdrehen um zwölf Stunden (aus 3 Uhr morgens wird nur 3 Uhr nachmittags), der Sinus ist »invariant« gegenüber jeder Vergrößerung von x um 2![]()
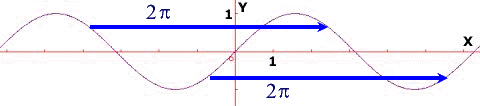 ";
";
...
| Der Mathematikunterricht sollte sehr viel mehr bzw. deutlicher auf solche "Invarianz" hinauslaufen, der gegenüber alle konkreten Werte und alles konkrete Rechnen sekundär (nur Hilfsmittel) sind.
|
Und wenn man solche Invarianz erst mal an ganz simplen Beispielen "kapiert" und als Grundprinzip der Mathematik verstanden hat, könnte man auch in der Schule durchaus zu dem übergehen, was bei Poncelet mit "Invarianzen" gemeint war:
"was bleibt »invariant«, wenn ich Gegenstände projiziere, bzw. was macht beispielsweise ein Rechteck - abgesehen von Kleinigkeiten - eigentlich aus?"
Und da kann man doch wunderbar mit Lampen und verschiedensten Projektionsflächen experimentieren; ich wette aber, dass der Unterricht dabei mehr auf "Verständnis" als auf Abprüfbares hinausläuft!
(die Projektion eines x-beliebigen Gegenstands
- und sogar ein ganzes ![]() )
)
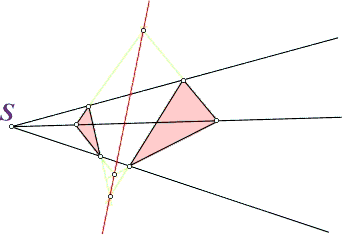
(Projektion eines Dreiecks auf eine Ebene)
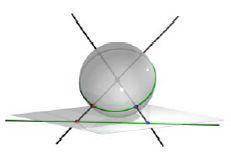
(Projektion einer Ebene auf eine Kugel oder umgekehrt)
![]() Von der Perspektive in der Kunst zur Relativitätstheorie
Von der Perspektive in der Kunst zur Relativitätstheorie

(eine Parabel erscheint aus Zentralperspektive als Ellipse)

(Bildquelle
![]() )
)
(bei solchen Kegelschnitten ganz unbedingt wichtig ist die kontinuierliche Verlagerung der Schnittebene und dabei die kontinuierliche Veränderung der Schnittgleichung)
Insbesondere interessant wären auch Ausflüge in die Kartographie, vgl. z.B.
.
Ausflüge in die Topologie:

Dann wird halt im Unterricht regelrecht geknetet!
| Solche Beschäftigung mit Invarianzen scheinen mir weit über die Mathematik hinaus von Bedeutung, bzw. dadurch überhaupt erst gewinnt Mathematik ihren Platz in der "Allgemeinbildung": |
es geht um
"Erziehung" zur Abstraktion
(was an einer Planskizze ist wichtig [substantiell] und was nicht [akzidentiell]?),
das Unveränderliche im Veränderlichen.
das Denken in Analogien und die kritische Unterscheidung, wann (in welchen Punkten) eine Analogie vorliegt und hilfreich ist - und wann nicht,
Und damit sind wir bei Poncelets zweitem, im Unterricht sicherlich schwierigerem und hier (vorerst?) nur angedeutetem Prinzip, der "Dualität".
"[...] wenn der eine [Satz] von ihnen bewiesen ist, gilt auch der andere ohne weiteren Beweis gemäß dem Prinzip der Dualität."
(E. T. Bell)
Das ja eben macht mathematischen Fortschritt zentral mit aus: dass neue, oftmals unscheinbare Erkenntnisse (oder "Abfallprodukte" wie etwa beim Beweis des "zu nichts brauchbarem" letzten Satzes von Fermat) nach dem Prinzip der Dualität dann auf ganz andere, ungeahnte Felder übertragen werden können.
Musterbeispiele waren da in der Mathematikgeschichte insbesondere die Mengen- und Gruppentheorie
(mit manchmal schier unglaublichen Analogien: beispielsweise bildet die Gesamtheit aller Rotationen eines regelmäßigen Ikosaeders
um seine Symmetrieachsen dieselbe "Gruppe" wie die der Permutationen der Lösungen [derjenigen x, für die sich y = 0 ergibt] von Gleichungen fünften Grades, also der Form y = ax5 + bx4 + cx3 + dx2 + ex + f;
oder einfach gesagt:. da kann eine sehr einfache geometrische Erkenntnis [Veranschaulichung!] direkt auf teuflisch schwierige Algebra übertragen werden, und das eine erklärt das andere, obwohl beide Dinge nichts [außer eben der Gruppenstruktur] miteinander gemeinsam haben.)
Ganz besonders wichtig ist aber die in der Schule immer wieder zu betonende, ja als Leitfaden zu benutzende und letztlich doch nach wie vor höchst erstaunliche Traumhochzeit von Algebra und Geometrie
"Jedes geometrische Problem ließ sich zumindest algebraisch ausdrücken, wenn schon nicht sofort lösen, und aus jeder Verbesserung oder Entdeckung in der Algebra konnte sich eine Anwendung oder Interpretation in der Geometrie ergeben. Die Kenntnisse über Raum und Zeit [...] wurden dadurch innig miteinander verflochten und unauflöslich miteinander verbunden. Von da an war es fast unmöglich, eine der beiden zu verbessern, ohne auch die andere zu verbessern. Das Problem, Tangenten an Kurven zu legen, führte zur Entdeckung der Differentiale, das der Längen- und Flächenberechnung zur Umkehrung der Differentiale, zu den Integralen, die Untersuchung der Flächenkrümmung zum Verfahren der partiellen Differentiale, das isoperimetrische Problem zur Variationsrechnung. Und umgekehrt fanden alle diese großen Fortschritte in der Algebra sofort ihre Anwendung auf die Geometrie und führten zur Entdeckung neuer Beziehungen zwischen Punkten oder Linien oder Flächen."

William Rowan Hamilton
(1805-1865)
Zu fragen wäre allerdings, wo sonst die Dualität in Schulen eingebracht werden könnte. Hier seien nur zwei Beispiele genannt:
dass, wer in der 10. Klasse die Exhaustionsmethode für Kreise begriffen hat, eigentlich auch schon (in der 12. Klasse) integrieren kann
(also bereits sehr viel mehr "erledigt" hat, als er ahnt);
dass der uralte "Satz des Pythagoras" unter Zuhilfenahme der Vektorgeometrie plötzlich äußerst einfach bewiesen werden kann.
Wichtig an solcher "Dualität" ist, dass
von derzeitigen Erkenntnissen im Unterricht aus immer auf andere (frühere oder spätere) Erkenntnisse ausgegriffen und somit ein "Netz" gebildet wird;
die Dinge, wenn möglich, immer von mehreren Seiten aus betrachtet werden, z.B.
ein Graph ist die Spur eines sich bewegenden Punkts
oder die Spur einer sich bewegenden Tangente:
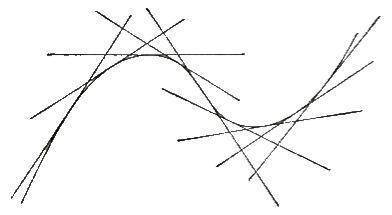
die markierte Zeile im pascalschen Dreieck
gibt einerseits die Koeffizienten an für (a + b)5
und zeigt andererseits: aus fünf verschiedenen Elementen können fünf Einzelelemente, zehn Paare, zehn Dreiergruppen sowie eine Fünfergruppe entnommen werden.