in Kiew
in Kiewdie Geometrie der Kanaldeckel  in Kiew
in Kiew
(was im Mathematikunterricht allerdings höchst ungewöhnlich ist)
immerhin die simpelsten Informationen über Kiew durchgenommen werden:
Hauptstadt der Ukraine (Lage in Europa),
aktuelle politische Lage in der Ukraine
wobei man sich natürlich fragen kann, was all das mit Kanaldeckeln zu tun hat: die von mir fotografierten Kanaldeckel [s.u.] sind großteils in miserabel schlechtes Pflaster eingebettet, was wohl auch ein Zeichen der Armut ist;
die Patina und den „shabby chic“ der Kanaldeckel findet aber vielleicht nur attraktiv, wer im Luxus lebt und dessen perfekte Glätte schon wieder satt hat),
ca. 3 Millionen Einwohner,
wunderschöne Innenstadt  ,
,
gigantische Hochhaus-Wohnviertel ringsum  .
.

Wenn man Kanaldeckel durchnimmt, geht es zudem nicht an, ihre Funktion auszublenden: sie sind Schnittstellen zwischen der Ober- und der meist unsichtbaren und damit fast unwirklichen Kanalisations-„Unterwelt“
(mit treffenden Metaphern auch als „Gedärm der Städte“ oder „Städte unter den Städten“ bezeichnet):
Kanaldeckel
schließen einerseits die Ober- von der Unterwelt ab
(damit keiner unfreiwillig in letztere hinunterfällt, aber auch, damit kein Unbefugter letztere betritt),
eröffnen aber andererseits auch den Zugang zur Unterwelt.
Kanaldeckel sind also Türen. Fast am interessantesten an Türen ist aber, was dahinter (darunter) ist:

Beim Begriff „Kanalisation“ denke ich aber natürlich
sofort an den Filmklassiker  und
insbesondere dessen legendäre Schlussszene:
und
insbesondere dessen legendäre Schlussszene:
Zwar gibt es in einigen Städten Führungen durch die Unterwelt der Kanalisation
(eben z.B. in Wien
aber mir ist nicht bekannt, ob es sowas auch in Kiew gibt.
(Dafür hat Kiew aber im Untergrund was anderes zu bieten, nämlich die teilweise 105,5 m unter der Erdoberfläche liegende und damit tiefste U-Bahn der Welt:
 )
)
Und selbst wenn es in Kiew eine Führung in die Kanalisation gäbe, kann man ja nicht einfach mal kurz „nur“ zwecks Kanalisations-Tour mit einer Schulklasse nach Kiew reisen.
Ein empfehlenswerter Ersatz ist aber das leider vergriffene und deshalb nur antiquarisch erhältliche Buch .
.| „Glotzt nicht beim Loben immer nur nach oben, schaut auch mal zur Seite [und wichtiger noch: nach unten  ], ],dann sehr ihr die Pleite.“ |
Warum in die Ferne schweifen, wo das Gute (Kanaldeckel) liegt so nah, nämlich direkt zu unseren Füßen?!
Überhaupt ist mir ja jedes (am besten alltägliche) Mittel recht, um den
„mathematischen Blick“  zu üben.
zu üben.
Und „mathematischer [und überhaupt wissenschaftlicher] Blick“ bedeutet ja u.a. Mustererkennung bzw. Muster-„making“:


Wie gesagt: das Gute liegt so nah: man muss nicht extra nach Kiew reisen, um interessante Kanaldeckel zu sehen, sondern es reicht,
(hier nur ein Beispiel aus Palma [Mallorca]:
 )
)
(denn am besten sind noch immer "be-greifbare" Kanaldeckel, vor denen Schüler sich hinsetzen und die sie abmessen können).
Nun sind allerdings die meisten Kommunen (aus Kostengründen?) arg phantasielos und verwenden Standard-Kanaldeckel à la
 .
.
Aber selbst an diesen Standard-Kanaldeckeln läßt sich viel lernen, nämlich z.B. die Punkt-, Achsen- und Drehsymmetrie:

Jetzt aber die Ergebnisse einer Kanaldeckel-Forschungsreise nach Kiew:











Darunter sind
 oder
oder 
(die aber gut für den Einstieg geeignet sind),
 ,
,  oder
oder  .
.
Ziel eines "Kiewer-Kanaldeckel-Unterrichts" ist es, dass die Schüler

Nun haben mir ja schon die Fachleiter während meiner Referendarszeit beigebracht, dass "verstehen" kein brauchbares Lernziel ist, da es sozusagen in den Köpfen der Schüler eingesperrt bleibt.
(Die Rolinck-Brauerei hat vor
Jahren die Crux der
Konstruktivismus-Mode mal schön auf den Punkt gebracht: „Es zählen die
inneren Werte. Nur wie kommen die da rein?“ [durch Biertrinken!])
Die beliebte Lehrerfrage, ob die Schüler etwas (z.B. einen Text) verstanden haben, ist ziemlich blöd, denn die direkten Antworten sind da wohl "ja", "teilweise" oder "nein".
(Wenn die Schüler fälschlich meinen, etwas verstanden zu haben, liegt das oftmals auch daran, dass ihr "Gedankenkonstrukt" durchaus in sich stimmig ist.)
Die Lehrer-Frage, ob die Schüler etwas verstanden haben, ist also oftmals rhetorisch: die mitgelieferte Antwort und fast schon bösartige Unterstellung ist da, dass die Schüler es sowieso nicht verstanden haben.
(und es vielleicht auch gar nicht verstehen wollen):
(Schule läuft allzu oft darauf hinaus, den Schülern zu zeigen, dass sie strunzdumm auf die Welt gekommen sind und erst mühsam schlau gemacht werden müssen.)
Das „gar nichts“ rührt oftmals auch daher, dass die Schüler nicht verorten können, was sie nicht und was sie durchaus verstanden haben: sie sehen dann einfach vor lauter Bäumen (Unverstandenem) den Wald (das durchaus Verstandene) nicht mehr.
Manchmal ist die Behauptung, etwas (gar) nicht verstanden zu haben, aber durchaus schlau, denn so ist der Lehrer fast gezwungen, es nochmals zu erklären.
(Aus dem gleichen Grund behaupten Schüler gerne: "Das haben wir [beim vorherigen Lehrer] noch nie gehabt.")
Mit durchaus gutem Grund wird immer vorausgesetzt, dass immerhin der Lehrer alles (richtig) verstanden hat. Und doch ist das manchmal penetrant besserwisserisch:
"»Ich habe bemerkt«, sagte Herr K., »dass wir viele abschrecken von unserer Lehre dadurch, dass wir auf alles eine Antwort wissen.«"
(Bertolt Brecht, Geschichten vom Herrn Keuner)

Aber zurück zum Ziel eines "Kiewer-Kanaldeckel-Unterrichts", nämlich dass die Schüler
Wie gezeigt, reicht 1., also "verstehen", allein nicht aus, sondern muss es "offenbar" werden, und zwar
(und zwar mehr als nur „ich habe es [nicht / teilweise] verstanden“),
Nehmen wir als erstes Beispiel  : hier könnten die Schüler
: hier könnten die Schüler
(denn oftmals sind [wie wir gleich nochmals sehen werden] die Hände schlauer als der Mund),
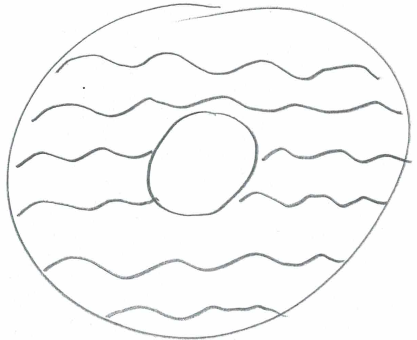
Ein zweites Beispiel ist  : obwohl das Muster hier kaum schwieriger ist als
: obwohl das Muster hier kaum schwieriger ist als  , läßt es sich
, läßt es sich
Und nur noch ansatzweise sagbar ist wohl
 :
:
Außenkreis, Innenkreis
außen Sternform,
innen achsensymmetrische "Blitze".
 ein
abstraktes Ornament oder ein stilisiertes Symbol [für
elektrischen Strom?] ?)
ein
abstraktes Ornament oder ein stilisiertes Symbol [für
elektrischen Strom?] ?)“Wovon man nicht sprechen kann, das muss man tun“:
ob die Schüler ein Muster erkannt / verstanden haben,
kann daran klar werden, ob sie es nachzeichnen / machen können.
Solches Nachzeichnen ist aber zugegebenermaßen „unnatürlich“:
mag ja noch sein, dass auch die Schüler dem ästhetischen Reiz der Kiewer Kanaldeckel erliegen,
aber wieso sollten sie den Wunsch haben, diese bereits fertigen Kanaldeckel nochmals nachzuzeichnen, also zu kopieren?!
Diese Frage zeigt ein erhebliches methodisch-didaktisches Problem auf, zu dem mir leider nur eine einzige Lösung (?) einfällt: der Lehrer gibt die Anweisung, die Kanaldeckel zu zeichnen.
Hinter dem gezeigten Problem steckt ein viel grundsätzlicheres:
beispielsweise in den heutigen
„Mitmach-Naturwissenschaftsmuseen“, aber auch in Wissenschafts(?)sendungen
wie  werden
oftmals spektakuläre und schöne Effekte gezeigt,
werden
oftmals spektakuläre und schöne Effekte gezeigt,
aber wie regt man das Publikum an, diese Effekte auch verstehen zu wollen?
(Man könnte fast sagen: indem die Museen und Sendungen nur die Effekte zeigen, aber kein [allzu kompliziertes?] Verständnis ermöglichen, machen sie Naturvorgänge nur [passend zu unserer kapitalistischen Zeit] konsumierbar und lenken sie somit nur von der eigentlichen Wissenschaft ab.)
Das „natürliche“ (nicht-mathematische) Kopieren eines Kanaldeckels sähe z.B. so aus: man setzt sich vor dem Kanaldeckel auf den Boden, legt ein großes Blatt Papier über ihn und fährt mit einem dicken Kohlestift darüber, so dass nur die Erhebungen auf das Papier übertragen werden
(der Fachbegriff dafür ist „Frottage“).
Also etwa so, wie man mit einem Bleistift eine Münze
kopieren kann: 
Für solches Kopieren braucht man allerdings keinerlei geometrisches Verständnis.
Wie bereits oben gesagt:
die normalen Kanaldeckel  sind arg langweilig,
sind arg langweilig,
und man kann ja nicht eben mal kurz mit einer Schulklasse nach Kiew fliegen.
Es bleiben also nur Fotos von (Kiewer) Kanaldeckeln, und die sind ja bereits Kopien. Wieso sie also nochmals kopieren?!

Heutzutage gibt es weniger Anlass zum Konstruieren denn je: wenn ich beispielsweise einen Kreis mit dem Durchmesser 30 cm brauche
(eine Größe, für die ich nichtmal einen Zirkel habe),
hole ich mir einen beliebigen Kreis aus dem Internet,
bringe ich ihn mit einem Bildbearbeitungsprogramm auf die richtige Größe
und drucke ihn dann aus.
Außerdem ist es eben doch schade, dass heutzutage alles so glatt & fertig ist, die Muster also vorgegeben sind und nicht mehr gemacht werden müssen / können.
Also mal angenommen, man findet
 elegant. Das mag
u.a. an der geschwungenen Seitenlinie
elegant. Das mag
u.a. an der geschwungenen Seitenlinie
 liegen. Aber
liegen. Aber
diese muss ja erstmal
(nach ästhetischen, mathematischen und Luftwiderstands-Kriterien)
entworfen
(d.h. ihr Muster muss erstmal gemacht)
werden,
um dann die „Blechbiege-Form“ herzustellen, mit der
in einem dritten Schritt die Bleche
(und mit ihnen die Seitenlinie)
hergestellt werden.
Bei der „Rezeption“ des Autos gibt es drei Schritte:
findet man es (komplett) elegant
(ein Impuls, der ja durchaus Selbstzweck sein darf!),
zerlegt man es „analytisch“ in verschiedene
elegante Teile, und eines davon ist die
Seitenlinie

(wobei natürlich die Beziehung der Einzelteile zueinander, also die harmonische Gesamtkomposition interessant bleibt),
schaut man sich die Einzelteile (die Seitenlinie) genauer an und versucht (u.a. mathematisch) herauszufinden, weshalb sie so elegant wirken
(wobei Eleganz letztlich vielleicht subjektiv und damit un-mathematisch bleibt).
Die meisten Menschen bleiben aber auf der ersten Stufe stehen - und erst mit der zweiten beginnt die Wissenschaft.
Nun wird die Herstellerfirma allerdings wohl kaum verraten, wie die Seitenlinie konstruiert wurde
(nach welcher mathematischen Formel?),
aber es läßt sich doch immerhin sagen, welche Form sie so ungefähr hat, nämlich die eines dreidimensionalen Sinus. Vgl. z.B.


(Nebenbei: ein besonders krasses Beispiel für derzeit moderne völlig
missglückte
Linienführung und damit Potthässlichkeit ist
 .
.
Im Vergleich damit finde ich ja sogar
 schön, weil
immerhin konsequent.)
schön, weil
immerhin konsequent.)

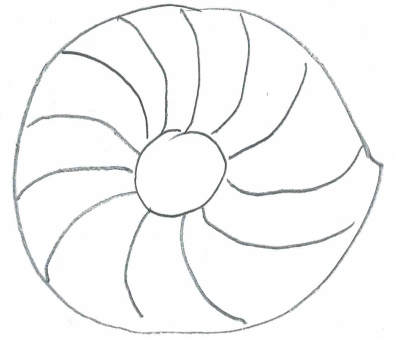
Erstes Beispiel eines nachzuzeichnenden Kanaldeckels sei
 ,
,
Daran lassen wir noch die "Ausbuchtungen" oben und unten und die kryptische (kyrillische) Beschriftung in der Mitte weg:

(Nebenbei: das Muster
dieses Kanaldeckels erinnert mich an Flugzeugdüsen
 - und solche
Eselsbrücken sind bei der Mustererkennung immer hilfreich: die Wirklichkeit
wimmelt von ähnlichen [Grund-]Mustern. Vgl. z.B. auch
- und solche
Eselsbrücken sind bei der Mustererkennung immer hilfreich: die Wirklichkeit
wimmelt von ähnlichen [Grund-]Mustern. Vgl. z.B. auch

 )
)
Nun ist zu fragen, in welchem Maßstab dieser Kanaldeckel nachgezeichnet werden soll. Am liebsten wäre mir ja die Originalgröße, da man dann in einer Ausstellung
(für die Abbildungen sehr groß sein müssen)
das Foto des Originals und die Konstruktionszeichnung nebeneinander hängen könnte.
Nun haben Schüler aber keine Zirkel, mit denen ein Radius von ca. 40 cm gezeichnet werden kann, und deshalb würde ich die Konstruktionszeichnung im Maßstab 1:5
(also mit einem Außenradius von 16 cm)
zeichnen lassen. Indem man die so entstehenden Konstruktionszeichnungen einscannt und auf dem Computer mit dem Faktor 5 vergrößert, kann man dann eben doch wieder die Originalgröße erreichen.
Sehr einfach ist noch die Konstruktion des Außen- und Innenkreises
(... wobei es für das Folgende sehr wichtig ist, den gemeinsamen Mittelpunkt der beiden Kreise deutlich zu markieren):

Schwieriger ist nun die Konstruktion der 16 (!) „Rippen“:

Die Rippen sehen aus wie Kreisteile bzw. Kreissegmente. Fragt sich nur, wo die (verloren gegangenen) Mittelpunkte dieser Kreise liegen, denn die Mittelpunkte braucht man, um mit einem Zirkel die Kreise (und damit Kreissegmente) zeichnen zu können.
Da muss man sich erinnern, wie man zu einem gegebenen Kreis seinen verloren gegangenen Mittelpunkt wiederfinden kann:
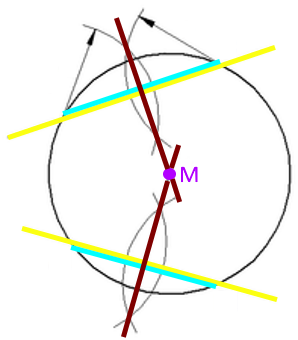
man zeichnet durch den Kreis zwei Geraden,
wodurch innerhalb des Kreises zwei Strecken entstehen.
Zu diesen Sekanten zeichnet man die beiden Mittelsenkrechten,
deren Schnittpunkt der gesuchte Kreismittelpunkt ist.
Nun ist dieses Verfahren bei unserem Kanaldeckel allerdings nicht so einfach anzuwenden, weil jede Rippe nur ein sehr kleiner Kreisausschnitt ist. Deshalb lohnt es sich, mit einem sehr großen Ausschnitt des Kanaldeckels zu arbeiten:
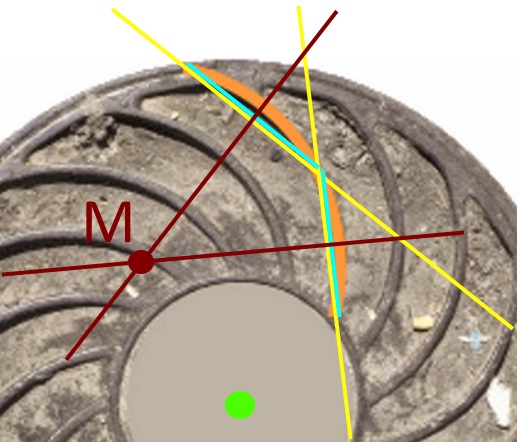
Mit diesem Mittelpunkt M und dem Radius r lassen sich nun der Kreis und das Kreissegment / die Rippe zeichnen:
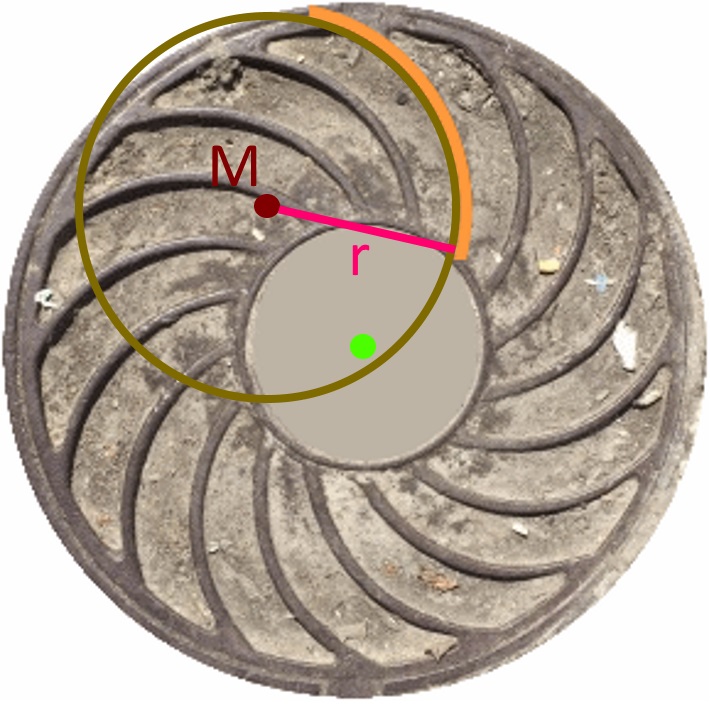
Wichtig ist jetzt noch die Entfernung e des Mittelpunkts M vom Mittelpunkt des Kanaldeckels:
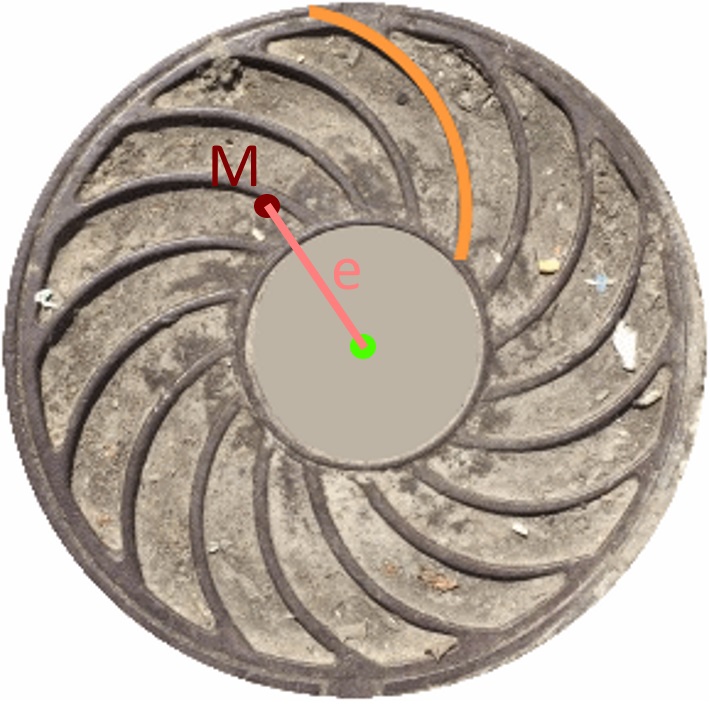
Die Mittelpunkte aller für die Rippen benötigten Kreise liegen also auf einem Kreis mit dem Radius e um den Mittelpunkt des Kanaldeckels:
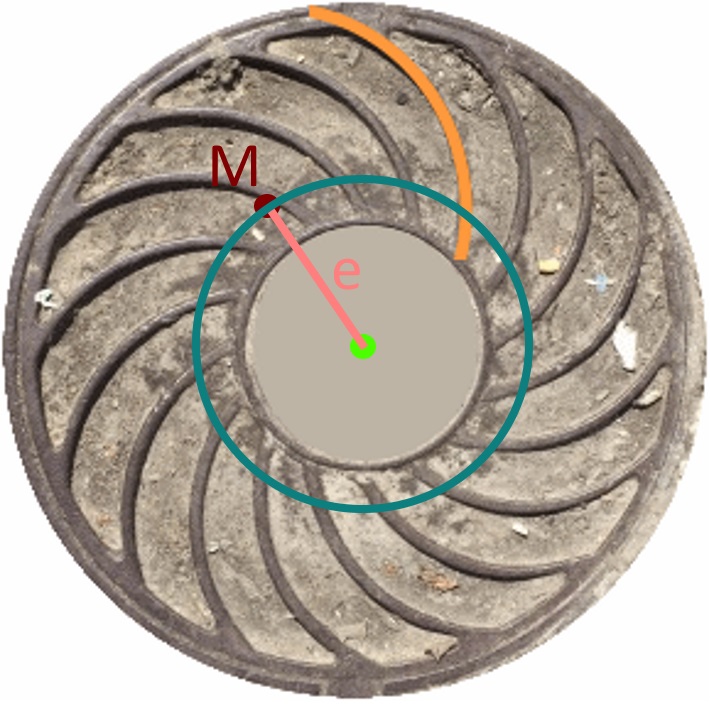
Wenn wir nun den Kreis
 in unsere
Anfangszeichnung
in unsere
Anfangszeichnung 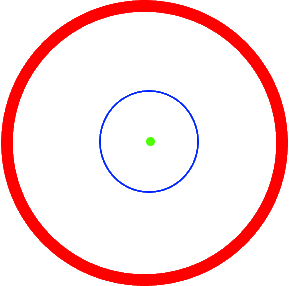 übertragen, ergibt sich
übertragen, ergibt sich
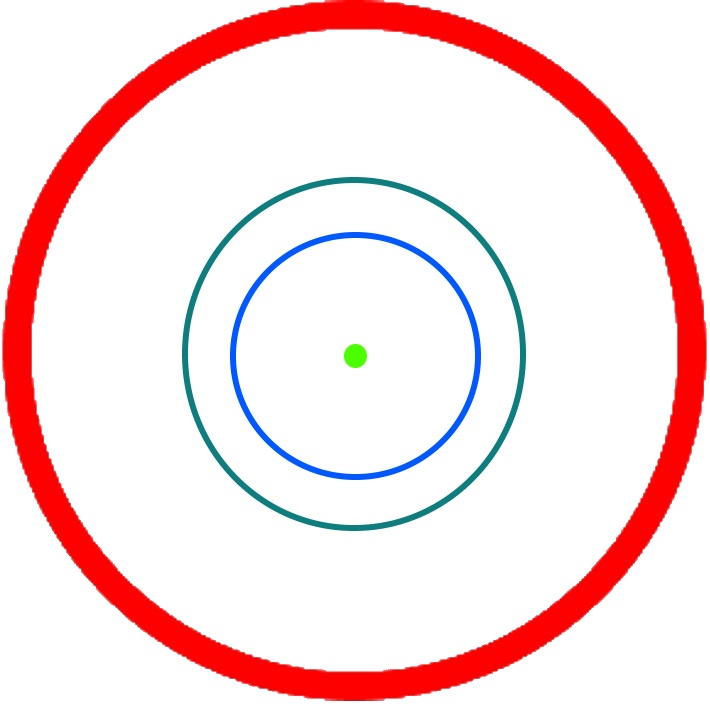
Um die 16 Rippen zu
zeichnen, brauchen wir 16 Kreise, deren
Mittelpunkte reihum auf dem Kreis
 liegen.
liegen.
Die gesuchten Mittelpunkte
sind auf 3600 verteilt, so dass alle
![]() =
22,50 ein
Mittelpunkt liegt:
=
22,50 ein
Mittelpunkt liegt:
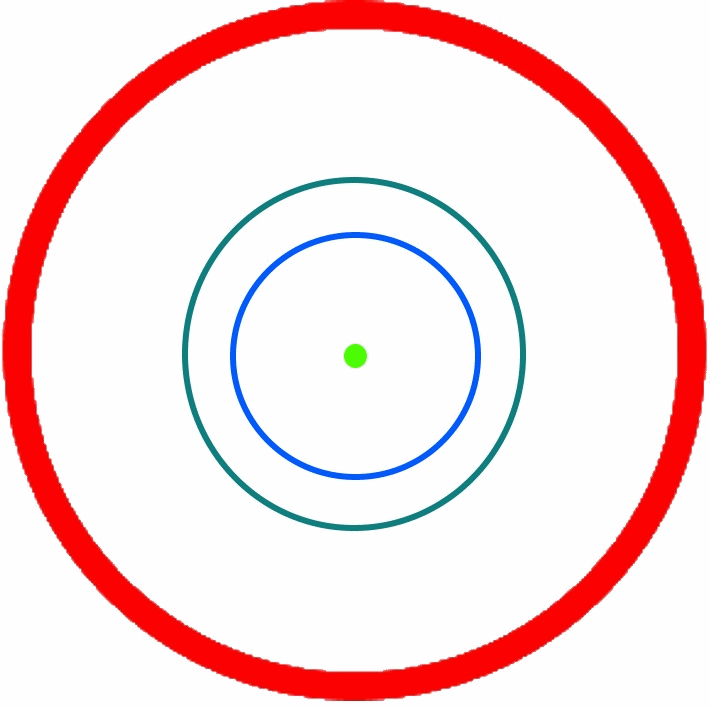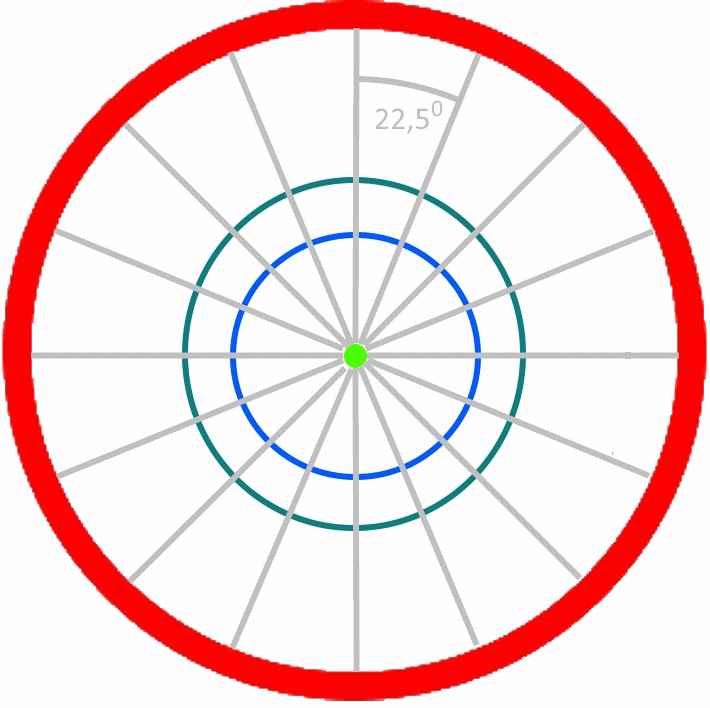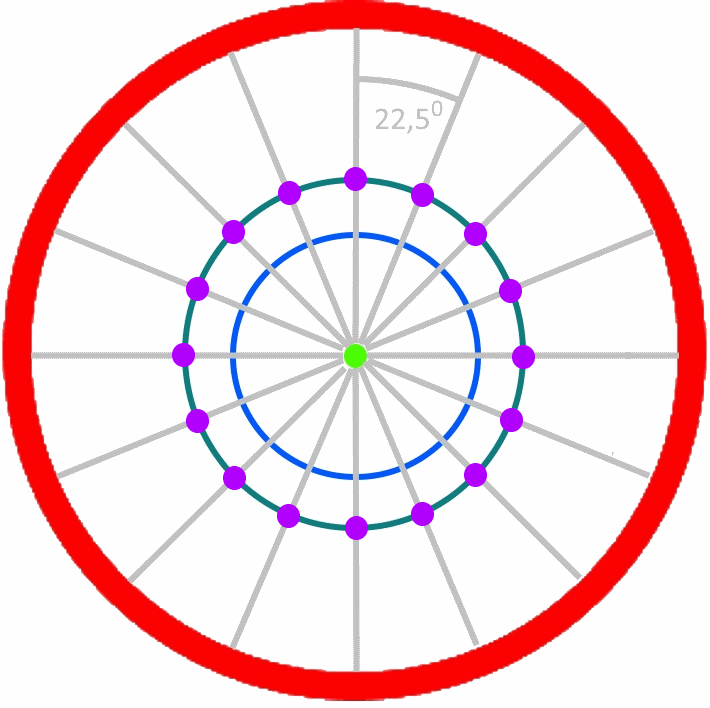
(Nun sind 22,50 sind auf dem Geodreieck schwer ablesbar. Deshalb eine Preisfrage: wie kann man ein Sechzehneck konstruieren?)
Für das weitere Vorgehen brauchen wir nur
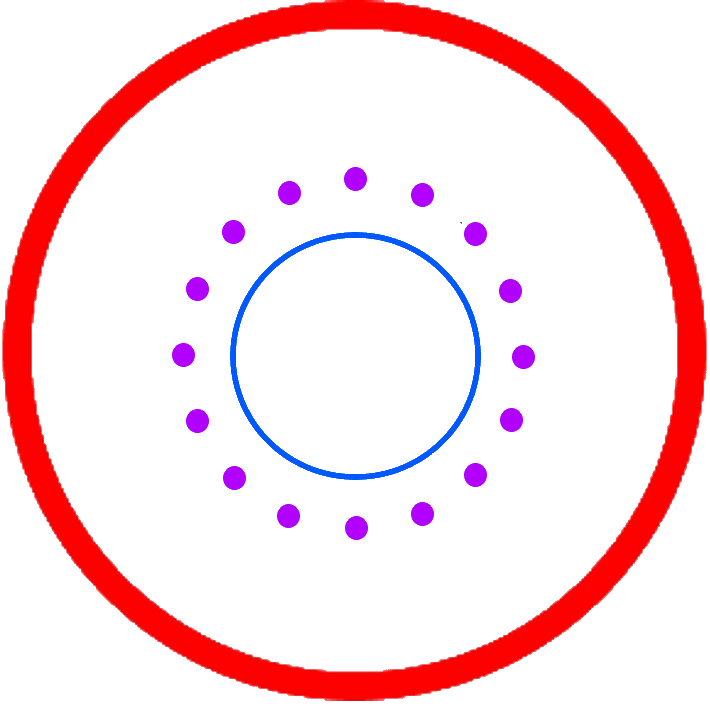 .
.
Nun zeichnen wir erst um einen Punkt • einen Kreis mit dem bereits oben ermittelten Radius r
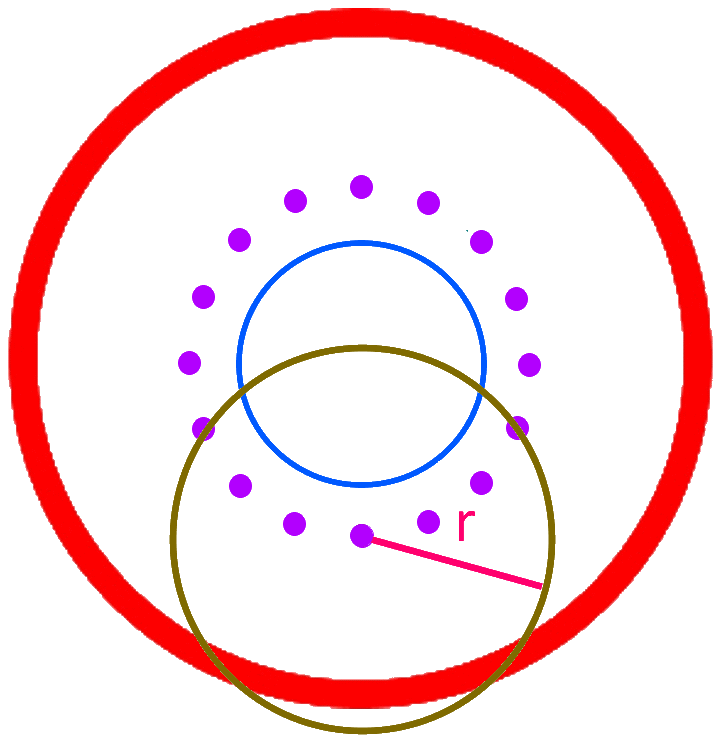
und dann um alle Punkte • :
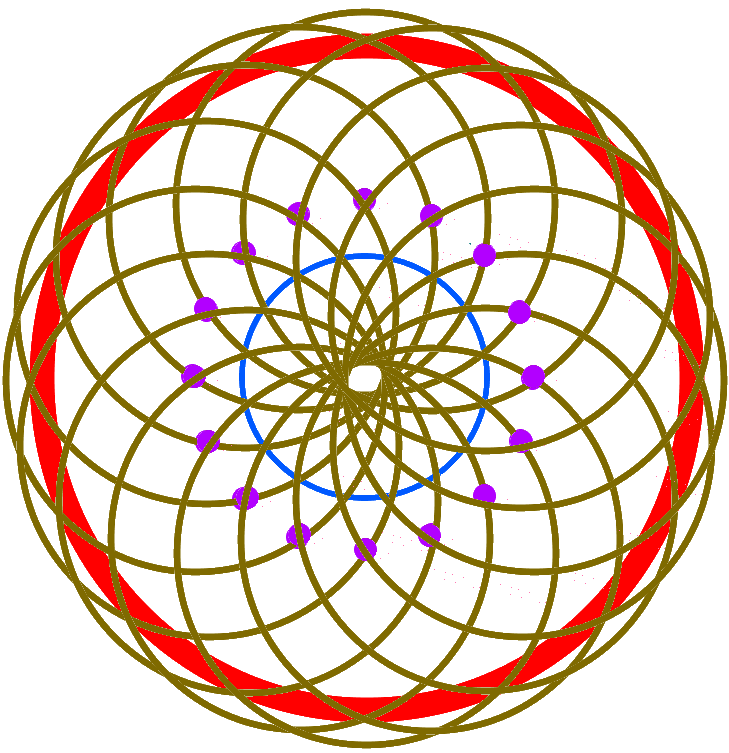

Obwohl ich auf dem fernöstlich-esoterischen Auge
blind bin, kommt es mir doch gerade recht, dass die Zeichnung
 an Mandalas
erinnert: die Schönheit von Mathematik kommt mir doch viel zu selten (als
Selbstzweck!) im üblichen Mathematikunterricht vor.
an Mandalas
erinnert: die Schönheit von Mathematik kommt mir doch viel zu selten (als
Selbstzweck!) im üblichen Mathematikunterricht vor.
Also nutzen wir
 doch mal zum
Ausmalen:
doch mal zum
Ausmalen:

Denn Mathematik muss auch mal
vom ewig gleichen abgenagten Zeichnen
zum (Aus-)Malen

und zuguterletzt zum Räumlichen
 ,
also zum prallen Leben
,
also zum prallen Leben
 kommen
kommen
(d.h. von der eindimensionalen Linie zur zweidimensionalen Fläche zum dreidimensionalen Körper [!]; denn [mathematisch!] streng genommen ist nichts in der äußeren Wirklichkeit ein- oder zweidimensional).
Der Normalsterbliche denkt ja wohl (wenn überhaupt) vom Drei- zum Zwei- zum Eindimensionalen
(der vollständigen Vereinfachung und Abstraktion),
der Mathematiker hingegen denkt meistens genau
umgekehrt: er
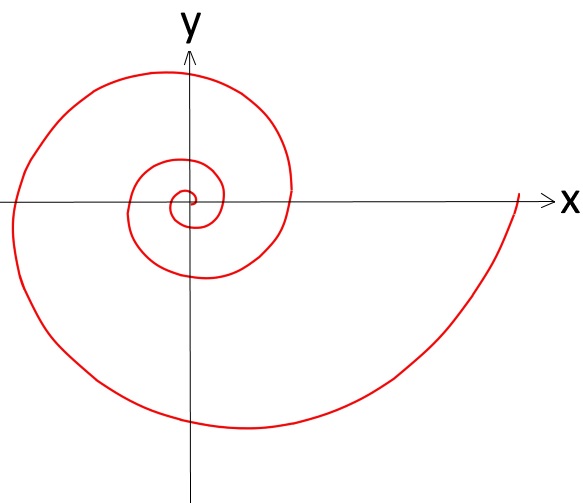
entwickelt erst (z.B. mit der Gleichung
![]() ) die
logarithmische Spirale
) die
logarithmische Spirale
 , und es
ist für ihn nur eine hübsche Dreingabe, dass sie auch in der Natur
vorkommt:
, und es
ist für ihn nur eine hübsche Dreingabe, dass sie auch in der Natur
vorkommt: 
(Nebenbei: die schönsten Mandalas werden nicht nur
zweidimensional ausgemalt, sondern von buddhistischen Mönchen
dreidimensional mit Farbpigmenten „aufgehäuft“:
 )
)

Wenn wir nun in
 noch die „Rippen“
markieren und alle Hilfspunkte und -kreise
weglassen, erhalten wir zuguterletzt
noch die „Rippen“
markieren und alle Hilfspunkte und -kreise
weglassen, erhalten wir zuguterletzt
 .
.
(Nebenbei: das Muster des Kanaldeckels
 taucht
auch anderweitig auf:
taucht
auch anderweitig auf:
 :
Einsaugöffnung einer Klimaanlage [ebenfalls in Kiew fotografiert],
:
Einsaugöffnung einer Klimaanlage [ebenfalls in Kiew fotografiert], : ein
Schwungrad [?] aus meiner Mechaniksammlung.
: ein
Schwungrad [?] aus meiner Mechaniksammlung.Bei diesen beiden Gegenständen hat die "Rippenform" allerdings vermutlich
mechanische Gründe, ist sie also nicht - wie beim Kanaldeckel
 - nur
Ornament:
- nur
Ornament:
 lenken die Rippen den Luftstrom,
lenken die Rippen den Luftstrom, sorgen die gekrümmten Rippen dafür [?], dass die Kräfte zwischen
Mittelachse und Außenrand gleichmäßig übertragen werden und die Rippen
nicht "weggeschert" werden, was leichter bei geraden Rippen
sorgen die gekrümmten Rippen dafür [?], dass die Kräfte zwischen
Mittelachse und Außenrand gleichmäßig übertragen werden und die Rippen
nicht "weggeschert" werden, was leichter bei geraden Rippen
 passiert.)
passiert.)Ein zweites Beispiel ist
 .
.
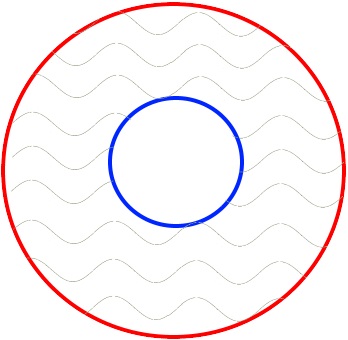
(Nebenbei: wenn das ein Wellenmuster sein soll, passt es besonders gut auf einen Kanaldeckel für einen Abwasserkanal.)
In einem ersten Schritt abstrahieren wir wieder den
Außen- und Innenkreis
 und erhalten
somit
und erhalten
somit  .
.
Jetzt kümmern wir uns aber erstmal um das Wellenmuster. Daran ist zu allererst bemerkenswert, dass alle Wellenlinien die gleiche Form haben und „gleich getaktet“ sind:

Wir nehmen uns daher erstmal nur eine einzige Welle vor:

bzw. vergrößert

und jetzt noch ausgeschnitten:

Hier scheiden sich nun die (Schüler-)Geister:
Schüler höherer Jahrgänge kennen den Sinus schon und können ihn hier anwenden,
die anderen kennen ihn noch nicht:
(was allerdings nur mal so nebenbei wohl kaum möglich ist;
immerhin soviel sollte allerdings möglich sein: wie
mag ein Sprayer diese Linie gesprayt haben?:
 Indem er
einfach [?] immer die Hand hoch und runter bewegt hat und gleichzeitig
an der Mauer entlanggegangen ist!
Indem er
einfach [?] immer die Hand hoch und runter bewegt hat und gleichzeitig
an der Mauer entlanggegangen ist!
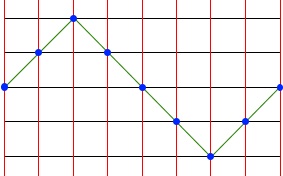
Wichtig dabei sind allerdings aufeinander abgestimmte Geschwindigkeiten:
 ;
;
 ;
;
erstaunlicherweise beherrscht aber fast jeder diese komplizierte, mal langsamere und dann wieder schnellere Auf- und Abbewegung - was so erstaunlich dann aber doch wieder nicht ist: man kann eine gleichmäßige Auf- bzw. Abbewegung nicht urplötzlich stoppen und danach prompt zu einer [wieder gleichmäßigen] Gegenbewegung übergehen, sondern ist gezwungen, die eine Bewegung langsam zu stoppen und dann wieder in Gegenrichtung zu beschleunigen;
der Mensch scheint also eine natürliche Fähigkeit zum Sinus-Zeichnen zu haben),
2. Möglichkeit: den Schülern wird einfach nur ein fertige Sinus-Schablone an die Hand gegeben:

Fragt sich nur, ob dieser (evtl. verkleinerte oder vergrößerte) „Fertig-Sinus“ annähernd mit den Wellen auf dem Kanaldeckel übereinstimmt. Und in der Tat:

Um Sinus-Graphen über die gesamte Breite des Kanaldeckels zeichnen zu können, benötigen wir die folgende, verlängerte Schablone:

Nun müssen wir uns nochmals ansehen, wie die neun (!) Sinuswellen auf dem Kanaldeckel angeordnet sind:

Da fällt auf:
: es liegt immer gerade der blaue, „halbhohe“ Punkt • der Sinuswelle auf der roten Mittellinie des Kanaldeckels;
: wenn zwei blaue Punkte • • jeweils eine Einheit e voneinander entfernt liegen, liegen oben bzw. unten ein blauer Punkt • und ein violetter Punkt • eine halbe Einheit e voneinander entfernt;
bzw. einfacher gesagt: wenn zwei blaue Punkte • • jeweils zwei Einheiten d voneinander entfernt liegen, liegen oben bzw. unten ein blauer Punkt • und ein violetter Punkt • eine Einheit d voneinander entfernt - und es gibt 18 solche Einheiten d auf der roten Mittellinie.
Das heißt aber, dass wir die rote Mittellinie in 18 Einheiten d unterteilen müssen.
Wenn wir all das beachten, erhalten wir
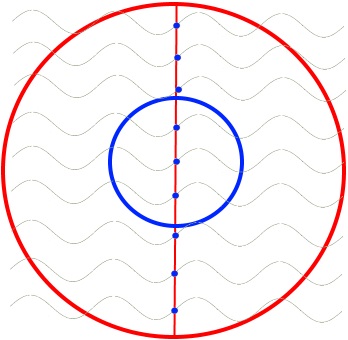 .
.
Nun lassen wir noch die rote Mittellinie und die blauen Punkte weg und erhalten
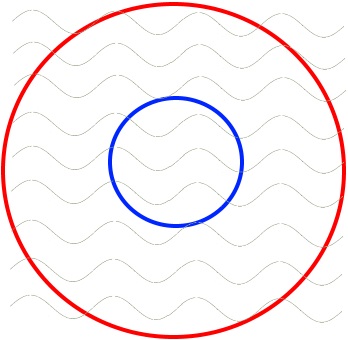
Und zuguterletzt löschen wir noch alles außerhalb des roten und innerhalb des blauen Kreises: