der Mensch ist für Kombinatorik nicht geschaffen

"Wenn das in der Klausur dran kommt, dann ..."
(ein Schüler)

Wenn es stimmt, dass der Mensch für Kombinatorik nicht geschaffen ist, so ist die Kombinatorik das glatte Gegenteil von .

"Der" Mensch = alle Menschen? Zumindest ich nicht - und, wie mir scheint, viele SchülerInnen auch nicht.

Mag allerdings sein, dass es Kombinatorikgenies gibt. Und mit ein bisschen Übung

(sowie unten gezeigten Tricks)

sieht man Vieles vielleicht auch schneller.

Wie auch immer: ich sehe die Lösung der folgenden, doch wahrhaft noch sehr einfachen Aufgabe nicht auf Anhieb:

"Wie groß ist die Wahrscheinlichkeit, bei zwei Würfelwürfen nacheinander eine gerade Summe zu erhalten?"

Als ich SchülerInneN in zwei verschiedenen Klassen mal diese Aufgabe stellte, kam als erste Antwort jeweils

(was nebenbei dasselbe wie ist),

und da ahnte ich, dass das sozusagen "richtig und doch falsch" war. Beide antwortenden Schüler konnten nämlich auf Anhieb nicht begründen, warum herauskommt. Einer stellte dann folgende These auf:

als Würfelsummen seien die Zahlen 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 möglich, und davon seien genau 6 Zahlen gerade (und 6 ungerade).  Also sei der Anteil der geraden Summen eben .

Da regte sich aber schnell Widerspruch:

dass nämlich die Würfelsumme 1 gar nicht vorkomme (also eine ungerade Zahl weniger) und somit nur die elf Zahlen 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 verblieben, von denen 6 gerade und 5 ungerade seien, so dass der Anteil der geraden Zahlen sei

(und ist größer als, d.h. so gesehen ist es wahrscheinlicher, eine gerade Summe als eine ungerade Summe zu würfeln).

Als die SchülerInnen derart (von mir auch absichtlich) verunsichert waren, griffen wir erstmal zum Baumdiagramm, das vollständig so aussieht:

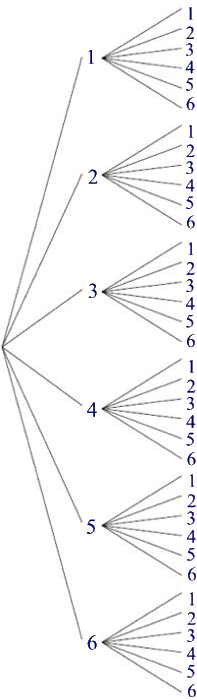
Das ist zwar (bei nur zwei Würfen) arg umständlich, aber doch oftmals das einzige Mittel, sich in all den Eventualitäten zurecht zu finden.

Man kann sich das Baumdiagramm aber vereinfachen, wenn man bedenkt, dass eine gerade Summe auf zwei Arten zustande kommen kann:

1. als Summe zweier ungerader Zahlen,
2. als Summe zweier gerader Zahlen.

Deshalb schauen wir uns exemplarisch an, was passiert

1. , wenn der erste Wurf ungerade, nämlich z.B. 1 ist,
2. , wenn der erste Wurf gerade, nämlich z.B. 2 ist:

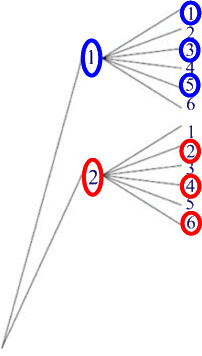
Offensichtlich bleiben dann

(egal, ob die erste Zahl gerade oder ungerade war)

im zweiten Wurf jeweils 3 Möglichkeiten, und das gilt natürlich genauso für die Zahlen 3, 4, 5 und 6 im ersten Wurf.

Insgesamt gibt es also 3 • 6 = 18 Möglichkeiten, eine gerade Summe zu würfeln, und das sind 18 von 36 Möglichkeiten, so dass sich die Wahrscheinlichkeit ergibt.

Und wenn ein Schüler mit geantwortet hätte, hätte ich, der ich die Aufgabe ja schon kannte, sofort "richtig" gesagt.

Nun ist aber auch gleich , so dass auch die anfängliche Antwort richtig und somit die Zwischenantwort falsch gewesen sein muss.

Wo aber lag bei  2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 der Denkfehler? Es kostet schon einige Mühe, es zu erkennen, und ist eben nicht intuitiv klar, dass die Summen 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 verschieden häufig vorkommen können, nämlich z.B.

• 2 auf nur eine einzige Art, nämlich als 1 + 1,
• 3 hingegen auf zwei Arten, nämlich als 1 + 2 oder 2 + 1,
• oder 5 sogar auf vier Arten, nämlich als 1 + 4 oder 4 + 1 oder 2 + 3 oder 3 + 2.

Nun bin ich allerdings zu faul, alle Möglichkeiten durchzuspielen, sondern mich interessiert der Trend: dass

• zwar mehr gerade Summen möglich sind,
• aber die beiden geraden "Ecksummen" 2 (1 + 1) und 12 (6 + 6) nur jeweils auf eine Art, also seltener.

Und das eben gleicht sich zur Wahrscheinlichkeit für gerade Summen aus

(vgl. ).

Nun stellen wir uns dasselbe Experiment

(Wahrscheinlichkeit für eine gerade Summe nach zwei Würfen)

mit einem Fünfer-"Würfel" vor.

Eigentlich brauchen wir dabei nicht einmal eine Vorstellung, wie solch ein Fünfer-"Würfel" aussehen könnte, aber es lässt sich eben doch schnell einer konstruieren:

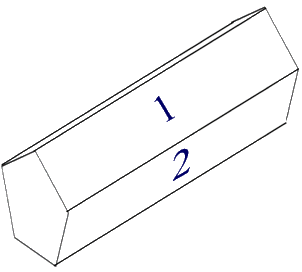
Jetzt müssen wir nur noch die Enden abrunden, damit der Fünfer-"Würfel" nicht auch auf diesen landen kann.

Die Schüler-Reaktionen waren nun:

1. : offensichtlich kommen unter den jetzt möglichen Zahlen 1, 2, 3, 4, 5 die geraden Zahlen seltener als die ungeraden vor, und deshalb wird die Wahrscheinlichkeit für eine gerade Summe kleiner als sein;
2. : ein Schüler ahnte allerdings schon, das sich das mit dem zweiten Wurf ausgleichen könnte, da ja auch die Summe zweier (häufiger vorkommender) ungerader  Zahlen gerade ist, und somit vermutete er, dass die Wahrscheinlichkeit für eine gerade Summe doch wieder sei.

Für eine Entscheidung blieb aber doch nur wieder ein Baumdiagramm, nämlich

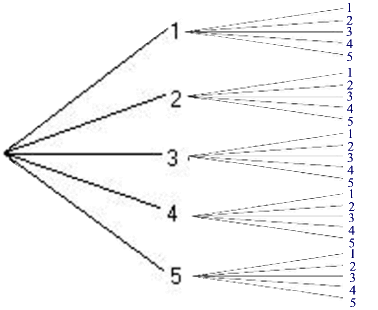
Eingedenk unserer Vorerfahrungen oben

(dass gerade Summen als Summe zweier gerader oder aber als Summe zweier ungerader Zahlen zustande kommen können)

schauen wir uns vorerst nur zwei Fälle an:

• eine ungerade Zahl im ersten Wurf, nämlich die 1,
• eine gerade Zahl im ersten Wurf, nämlich die 2.

Damit reduziert sich unser Baumdiagramm vorerst auf

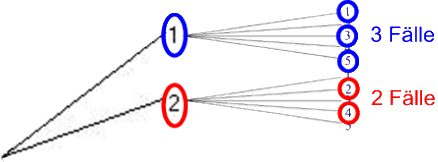
Und analog ergibt sich natürlich für die anderen Zweige:

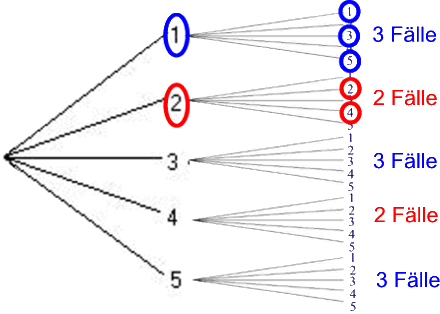
Wir erhalten also eine gerade Summe in 3 + 2 + 3 + 2 + 3 = 13 von insgesamt 25 möglichen Fällen, d.h. die Wahrscheinlichkeit für eine gerade Summe ist hier   und damit wider alles Erwarten (alle Intuition) sogar ein bisschen größer als .

Auf die Dauer kann man sowas wohl auch

(wie gezeigt anhand ausgewählter Zweige)

 im Kopf überschlagen. Aber dennoch hätte das wohl niemand intuitiv voraussagen können. Da versagt nun endgültig - und zwar (nochmals gesagt) in einem doch noch sehr einfachen Fall - unsere Intuition bzw. widerspricht die Kombinatorik aller (ersten) Anschauung.

Musterbeispiel für die Unanschaulichkeit der Kombinatorik ist aber .