warum einfach  , wenn's auch kompliziert  geht?

Gymnasiallehrer: "Ich foliiere."
Hauptschullehrer: "Ich tüte ein!"

Um einen Kreis zu zeichnen, legt man üblicherweise erst den Mittelpunkt fest (den man somit schon hat!), und der Kreis ist dann die Menge aller Punkte, die gleich weit vom Mittelpunkt entfernt ist:

Oftmals ist's aber genau umgekehrt: man hat einen fertigen Kreis und möchte

(z.B. dann, wenn man zu einem runden Tisch eine Tischdecke sucht)

nachträglich den nicht markierten Mittelpunkt

(oder den Durchmesser bzw. Radius)

bestimmen.

Auch bei der oben gezeigten Methode, den Kreis "freihand", also  ohne Zirkel zu zeichnen, kann man hinterher nicht mehr den Kreismittelpunkt sehen - und schon stellt sich die Frage, wie man ihn nachträglich doch wieder herausfinden kann.

Man kann das natürlich sehr umständlich machen, nämlich so, wie auch ich es bisher immer meinen SchülerInneN "beigebracht" habe:

  (Ohne Begründung: man zeichnet zwei beliebige Sekanten und dann zu jeder die Mittelsenkrechte. Die beiden Mittelsenkrechten schneiden sich dann im Keismittelpunkt.)  

Jüngst hat mir aber eine Hauptschullehrerin gezeigt, wie es viel einfacher geht: 

 

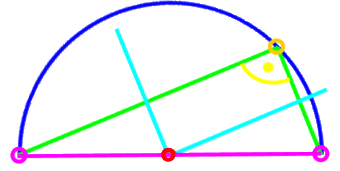
  (Man legt die Spitze des Geodreiecks in einen beliebigen Punkt auf dem Kreis und markiert dann die beiden Punkte, in denen die Katheten des Geodreicks den Kreis schneiden. Die Verbindungsstrecke dieser beiden Punkte ist der Kreisdurchmesser.

Dabei brauchen wir vom Geodreieck nur den rechten Winkel, aber sonst keine seiner Markierungen. Jeder andere rechte Winkel würde also auch reichen.)		  

Meine Reaktionen:

  1. ein Staunen, dass es so einfach geht;
  2. ein kleines Entsetzen, dass ich das so lange nicht gewusst habe;
  3. nicht ein Zweifel daran, dass die Konstruktionrichtig ist

(tatsächlich den Durchmesser ergibt),

wohl aber die Frage, warum das so ist

(also die Frage nach dem Beweis).

 

Nun ist aber (fast) nur ein Spezialfall von , denn um aus dem zweiten den ersten Fall zu machen, muss man nur

  1. die beiden Sekanten von einem Punkt ausgehen lassen:

,

  1. die beiden Sekanten zusätzlich senkrecht zueinander stellen:

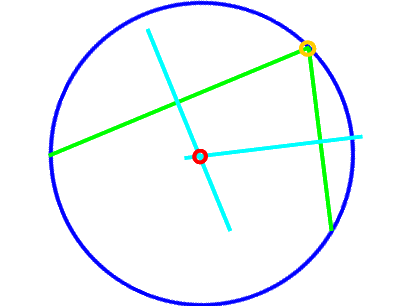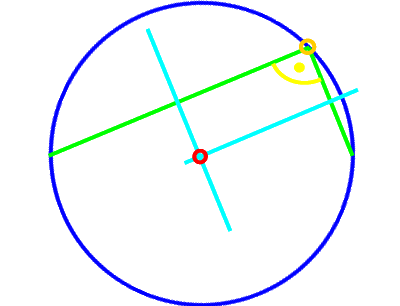
Auf diese Weise erhält man zweifelsohne wieder den Kreismittelpunkt.

Aber ist die Verbindung der beiden Sekantenpunkte dann auch tatsächlich

(wie in )

der Durchmesser - und geht diese Verbindungsstrecke tatsächlich genau durch den Kreismittelpunkt? Es sieht ja immerhin annähernd so aus:

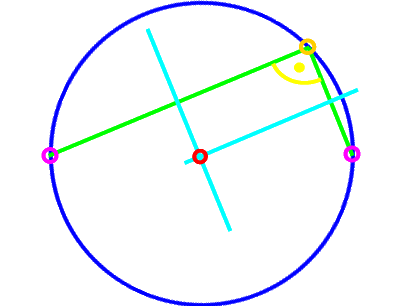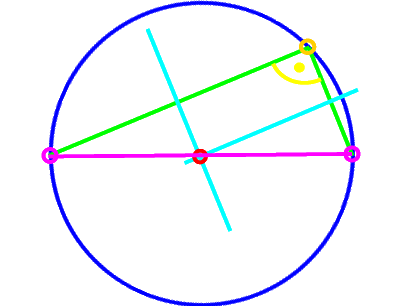
Nur ist "annähernd" natürlich kein mathematisches Argument. Es könnte ja sein, dass

  1. die Verbindungsstrecke fast unsichtbar knapp am Kreismittelpunkt vorbei geht,
  2. wir durch puren Zufall ein besonders günstiges Beispiel gewählt haben, dass also bei anderen Beispielen die Verbindungsstrecke sehr auffällig am Kreismittelpunkt vorbei geht.

Nun gilt:

WENN die Verbindungsstrecke tatsächlich der Kreisdurchmesser ist

(was wir aber eben noch nicht mit Sicherheit wissen!),

dann

Dass das Dreieck aber rechtwinklig ist, wussten wir schon vorher, d.h. wir haben nur einen Zirkelschluss durchgeführt:

rechtwinklig ... rechtwinklig

Erinnern wir uns kurz, was das Folgerungszeichen (nicht) bedeutet:

(beispielsweise kann der Regen schon aufgehört haben, die Straße aber noch immer nass sein);

                man  zeichnet ein rechtwinkliges Dreieck in einen Kreis ein die Hypotenuse des Dreiecks halbiert den Kreis
                                                                                                                    und ist daher sein Durchmesser.

 **

Den Satz des Thales werden wir weiter unten aber dennoch noch brauchen.

Nebenbei: ich ahne, was notorische Nichtmathematiker denken werden: dass das alles

(wie auch die Frage, ob die Dreieckshypotenuse in  wirklich durch den Kreismittelpunkt geht und somit der Kreisdurchmesser ist)

spitzfindig und somit überflüssig ist.

Halten wir nochmals fest, was noch nicht bewiesen ist, sondern erst bewiesen werden soll:

 man  zeichnet ein rechtwinkliges Dreieck in einen Kreis ein die Hypotenuse des Dreiecks halbiert den Kreis
                                                                                                     und ist daher sein Durchmesser.

 **

Nehmen wir aber mal an, die Hypotenuse AB unseres Dreiecks ABC halbiere nicht den Kreis, liege also neben dem Durchmesser AD:

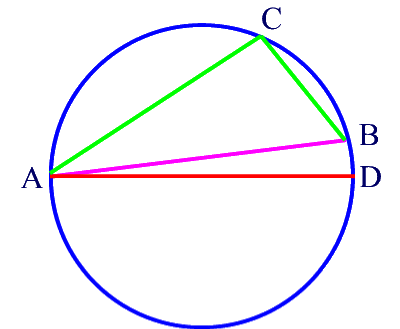
Dann hat das neue Dreieck ADC laut dem Satz des Thales bei C einen rechten Winkel:

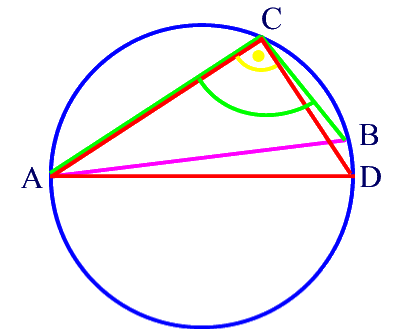
Und dann hat unser Ausgangsdreieck ABC bei C offensichtlich keinen rechten Winkel

(sondern einen größeren oder gegebenenfalls kleineren).

Das aber widerspricht unserem Konstruktionsanfang, den wir schließlich mit einem rechtwinkligen Geodreieck durchgeführt hatten.