Kuchengeometrie

Mein besonderer Dank gilt den SchülerInnen "meiner" derzeitigen (5/08) Klasse 9a

• Rachel Blume und Katharina Marguc, die den Kuchen gebacken haben,
• Charlotte Lips, die die Fotos gemacht hat.

Das (Doppel-)Problem:

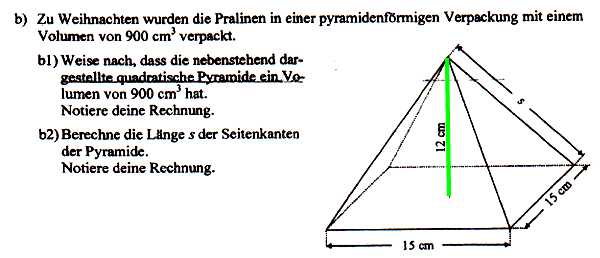
Bei der Lösung der ersten  Teilaufgabe b1) stellt sich die Frage:

wie lautet die Formel für

das Volumen einer Pyramide? Sowas weiß man natürlich nicht auswendig, sondern das schlägt man in einer Formelsammlung nach, wo steht:

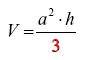
D.h. das Volumen einer Pyramide ist die Grundfläche mal die Höhe durch 3.

Das kann man natürlich einfach so hinnehmen - oder sich doch ein wenig wundern:

• da das Volumen des Quaders gleicher Grundfläche und gleicher Höhe V = a² • h ist,
• ist das Volumen der Pyramide also exakt ein Drittel so groß wie das des zugehörigen Quaders , bzw. die Pyramide passt exakt drei mal in den zugehörigen Quader .

Wenn man also aus dem Quader die Pyramide herausschneidet, muss der übrigbleibende Rest 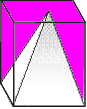dasselbe Volumen haben wie zwei Pyramiden, bzw.

(... was unten nicht bewiesen, sondern "nur" veranschaulicht werden soll.)

Darauf wird zurückzukommen sein. Vorweg aber etwas, was das Drittel um so erstaunlicher erscheinen lässt:

das Volumen eines Kegels 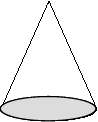wird mit der Formel

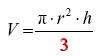
berechnet.

D.h. das Volumen eines Kegels ist die Grundfläche mal die Höhe durch 3 (!).

Also gilt:

• da das Volumen des Zylinders gleicher Grundfläche und gleicher Höhe V = π r² • h ist

• ist das Volumen des Kegels also exakt ein Drittel so groß wie das des zugehörigen Zylinders , bzw. der Kegel passt exakt drei mal in den zugehörigen Zylinder .

Wenn man also aus dem Zylinder den Kegel herausschneidet, muss der übrigbleibende Rest 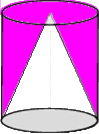dasselbe Volumen haben wie zwei Kegel, bzw. 

Daran finde ich allemal bemerkenswert:

1. dass beides Mal die 3 auftaucht,
2. dass die Pyramide ebenso exakt (!!!) 3 mal in den zugehörigen Quader passt wie der Kegel in den zugehörigen Zylinder.

(... was natürlich Zusammenhänge sind, die man nur entdeckt, wenn man sowohl die Pyramiden- als auch die Kegelformel kennt, also schon einen gewissen überblick hat.)

Kommen wir damit zur zweiten Teilaufgabe von

,

also zu b2): die besondere Schwierigkeit hier ist, dass

1. unsichtbare Hilfslinien benötigt werden und
2. zwei(!)mal der (gar nicht mitbenannte) Satz des Pythagoras angewandt werden muss

(Vgl. auch ).

Insgesamt ergeben sich damit zwei Probleme = Aufgaben:

• zu b1):

Wenn man aus dem Quader die Pyramide herausschneidet, muss der übrigbleibende Rest dasselbe Volumen haben wie zwei Pyramiden, bzw.

• zu b2):

es werden unsichtbare Hilfslinien benötigt.

Bei beiden Problemen habe viele SchülerInnen erhebliche Anschauungsprobleme, und zwar insbesondere, weil üblicherweise nur zweidimensionale Projektionen (Zeichnungen im Buch / an der Tafel / im Heft) angefertigt werden bzw. vorliegen.

Besser noch als ein dreidimensionales Fertigmodell wäre jedoch eins, anhand dessen die SchülerInnen die Zusammenhänge selbst entdecken bzw. überhaupt erst herstellen könnten.

Und das beste Modell ist immer noch ein selbstgebautes, da man oftmals erst beim Bau solch eines Modells

• die zu modellierende Zusammenhänge,
• Grenzen und Möglichkeiten der Modellierung

versteht - und sowieso beim ersten Mal alles erhellend falsch macht.

Selbstgemachte Modelle haben zudem den Vorteil, dass man endlich mal was Anfassbares hat, auf das man stolz sein kann, weshalb zumindest einige SchülerInnen sich dann manchmal auch besonders große Mühe geben

(vgl. beim Kuchen den zur Aufgabenbearbeitung eigentlich unnötigen Schokoladenüberzug).

Urplötzlich und mitten im Unterricht kam mir die Idee mit dem Kuchen, der allemal besondere Vorteile hat:

1. ist das benötigte "Material" leicht erhältlich und solch ein Kuchen relativ einfach anzufertigen,
2. lässt sich solch ein Kuchen sehr leicht schneiden.

Hier nun also das Meisterwerk in wichtigsten Etappen:

1. 
   der Ausgangskuchen, allerdings schon mit den ersten Schnittmarken versehen;
2. 
   der erste Schnitt (wobei die Schnitte durchaus einiger Vorüberlegungen bedürfen);
3. 
   der erste Rest (links) wird weggelegt; 
4. 
   das erste Zwischenergebnis;
5. 
   zweiter Schnitt mit zweitem Rest (links);
6. 
   nächster Rest (links) mit endlich freigelegter Pyramide; 
7. 
   die Pyramide von oben (mit dem bildschönen Retro-Kuchenteller :-);
8. 
   die für Aufgabe b2) halbierte Pyramide mit der ersten Hilfslinie - - -;
9. 
   Seitenansicht der halbierten Pyramide mit erster - - -und zweiter Hilfslinie ---;
10. 
    alle Reste;  
11. 
    Ausgangspyramide (rechts oben) und aus den Resten rekonstruierte zweite Pyramide (links unten);  
12. 
    danach immer noch übriggebliebene Reste, aus denen noch eine dritte Pyramide herstellbar sein müsste, was uns allerdings nicht gelungen ist (warum nicht?).

Es sei hier allerdings frischweg eingestanden, dass man die Zusammenhänge ( 3 , Hilfslinien) wohl nur entdecken (zurechtschneiden) kann, wenn man schon vorweg von ihnen weiß.

Aber ich vertraue darauf, dass man sie in später
en Aufgaben leichter entdeckt (hinein sieht), wenn man sie mal handgreiflich hergestellt und angefasst hat.