bildschöne Kurven

Wer bei "schöne Kurven" reflexartig an denkt

(Männer erinnern mich nicht an [geschwungene] Kurven, sondern an Geraden [s.u.]; vgl. auch ),

liegt natürlich zwar nicht falsch, aber mir geht es hier doch um (wenn auch in einem erweiterten Sinn) mathematische Kurven.

Dabei hätte ich allerdings auch nicht die mindesten Skrupel, einen Versuch zu starten, die Schönheit von Körperkurven mit mathematischen Mitteln zu untersuchen. Vgl. : nicht, um die Körperkurven mathematisch "abzunagen", sondern um ihnen zu huldigen!

Die einfachste mathematische (Eben-Nicht-)Kurve ist zweifelsohne die Gerade: sie geht verlässlich immer hübsch geradeaus, was sicherlich auch seinen ganz eigenen rasanten Reiz hat

,

aber eben doch auch so langweilig ist wie das Leben eines verbeamteten Reiheneigenheimbesitzers oder wie ein Highway am Ende der Welt:

Ein "richtiger" Motorradfahrer wird doch niemals Autobahnen entlang rasen

(womit er dann an einem Tag einen 1000 km langen, 1m breiten Asphaltstreifen gesehen hat),

sondern geschwungene Wege suchen:

Mathematisch gesagt: mit der Geradengleichung y = ax + b ist auch schon alles gesagt, nämlich dass die Gerade in alle Ewigkeit unverändert die Steigung a haben wird

(und b, also der y-Achsenabschnitt, regelt vollständig die Höhe bzw. Lage der Geraden):

Gähn!

Dennoch wollen wir die Geraden mathematisch nicht allzu gering schätzen: selbst die schlauesten Mathematiker können nicht direkt mit wirklich krummen Graphen umgehen, sondern müssen immer (etwa bei der Ableitung und der Integration) den Umweg über die Annäherung des Krummen durch Geraden gehen.

Geraden sind also schnödes, aber unverzichtbares Handwerkszeug, etwa so wie ein Hammer und Meißel:

Merkwürdig, dass man sich früher, in armen Zeiten, solche feingeschwungenen Treppen(geländer) leisten konnte

(aber damals konnte man sich ja auch noch massenhaft Feiertage leisten)

- und heute nicht mehr.

Als letztens in unserem Haus das Treppenhaus neu gestrichen werden musste, wollten wir - wie in alten Zeiten - auch einen  "Sockel" haben, und zwar derart, dass er parallel zu der Treppen"wange" lief:

Erst dadurch wurde ich überhaupt auf diese hölzerne "Wange" und ihre "krumme" Verlaufsform aufmerksam.

Da der Flur arg klein ist, ist es leider nicht möglich, die Gesamtwange auf ein Foto zu bekommen, weshalb sie hier in einer Fotomontage gezeigt sei:

Nun stellte sich mir die Frage, wie denn eigentlich die schön geschwungene Form der "Wange" zustande kam.

Dazu erstmal die prinzipielle Bauform der Treppe:

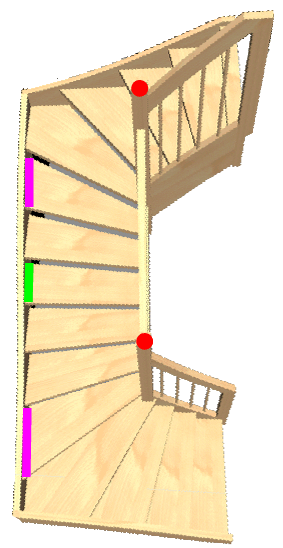
(Man nennt das wohl auch "2 x ¹/₂ gewendelt".)

Weil die Stufen aber um die "Wendelpunkte" "gefächert" sind, sind sie deshalb natürlich  dort auch breiter als die Stufen in der Mitte.

(Wie sich das genau ergibt, sei hier nicht weiter untersucht.)

Dabei sehen die "Wendelpunkte" an unserer Treppe folgendermaßen aus:

• oben: 
• unten:

Aber zurück zu "an der linken Wand breiter als die Stufen in der Mitte":

unsere Treppe hat folgende Maße:

• Höhe aller Stufen: 18cm
• Breite der Stufen an der langen Wand entlang:
  • 45 cm,
  • 33 cm,
  • 25 cm,
  • 25 cm,
  • 25 cm,
  • 25 cm,
  • 32 cm,
  • 35 cm,
  • 48 cm.

Nun verläuft die "Wange" immer 5 cm oberhalb der vorderen Treppenkante:

Damit ergibt sich als Höhe der Wange über der nächsttieferen Stufe 18 cm + 5 cm = 23 cm.

Als Stufenlinie an der Wand ergibt sich:

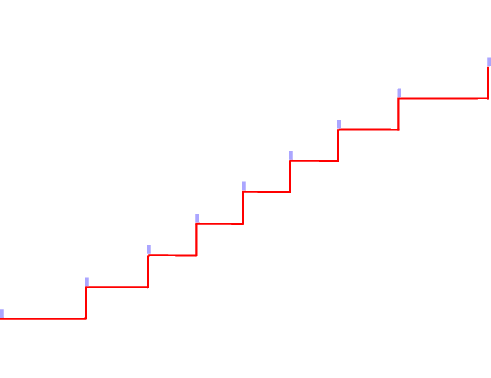
Die einfachste Möglichkeit, nun die Wange zu konstruieren, bestünde darin, die obersten Punkte der hellblauen Linien mit Geradenstücken (Strecken) zu verbinden:

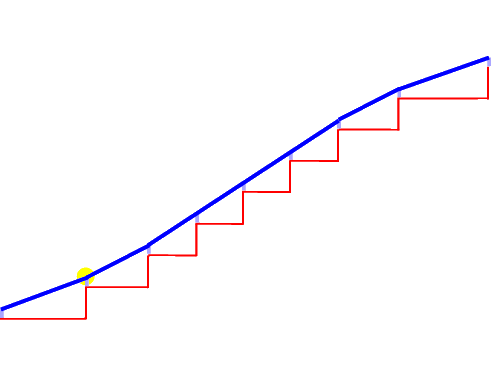
Dieses Ergebnis ist aber noch unschön, weil sich keine "geschwungene" Linie ergibt, sondern noch Knicke vorhanden sind, wie man besonders gut in der Vergrößerung sieht:

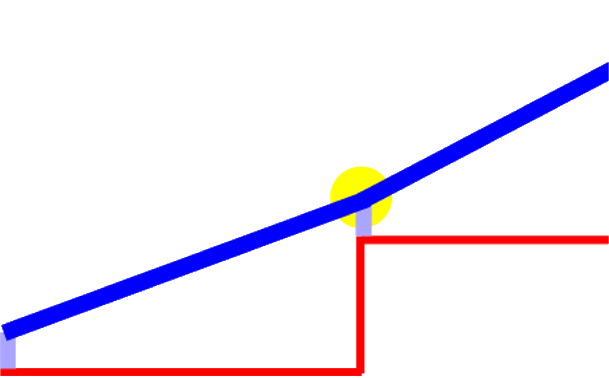
Wie nun aber bekommt man eine schön geschwungene, also knickfreie Wange hin?

Da gibt es verschiedene Möglichkeiten:

1. in der Oberstufe, indem man die Koordinaten der einzelnen Punkte in eine geeignete Gleichung eingibt. Das sei hier aber nur kurz erwähnt, weil es wohl kaum gelingen wird, eine einfache Gleichung zu finden, deren Graph durch alle Punkte geht.

Man kann sich da allerdings auch durch mathematische oder grafische Spline- bzw. Bezierkurven-Programme helfen lassen, wobei es doch allemal interessant wäre, ansatzweise herauszufinden, wie diese funktionieren bzw. rechnen.

(Ein empfehlenswertes Freeware-Übungsprogramm zu Splines wie überhaupt schönen Graphen ist nebenbei

"Spline" .)

Solch ein Programm liefert für unser Problem dann beispielsweise folgende Lösung:

2. - und das ist wirklich zentral wichtig - sollten die SchülerInnen auf die Dauer lernen, "freihand" eine geschwungene Linie durch die Punkte zu legen. D.h. sie sollten ein "Gespür" für geschwungene Kurven entwickeln.

Ratsam ist es da, erst mit Bleistift eine geeignete Kurve zu stricheln, sie langsam nachzubessern - und erst dann die endgültige, kräftig durchgezogene Kurve zu zeichnen.

Es gibt aber auch schöne - und in Schulen viel zu selten genutzte - Hilfsmittel, um geschwungene Kurven hin zu bekommen:

1. sogenannte Burmester-Kurvenlineale:

"Der Burmester-Satz z. B. besteht aus Splines dritter Ordnung und es lassen sich damit (praktisch) alle stetigen Funktionen annähern."
(Quelle:   )

Einfacher gesagt: die Burmester-Kurvenlineale sind aus so vielen verschiedenen krummen Linien gebildet, dass sich fast immer eine finden lässt, um einige vorgegebene Punkte harmonisch geschwungen zu verbinden.

2. sonstige "Kurvenlineale":

"Es gibt auch Kurvenlineale aus Gummi, die an eine Funktionsgleichung angepasst werden können. Im inneren bestehen sie aus einem Bleikern mit quadratischem Querschnitt; rechts und links davon befindet sich ein flacher Streifen Federstahl, damit das Kurvenlineal sich möglichst nur in einer Ebene biegen lässt. Biegsame Kurvenlineale sind in verschiedenen Längen zwischen ca. 300 mm und ca. 1000 mm erhältlich."
(Quelle:   )

Vorteil dieser biegsamen "Lineale" ist, dass sie sich aufgrund ihrer (mir fehlt das Fachwort:) "zähflüssigen" Konsistenz kaum in Knicken, sondern fast nur in harmonischen Schwingungen biegen lassen - und damit regelrechte Vorbilder aller stetig-differenzierbaren Funktionen sind, also solcher, die mit einem Strich ohne Knicke zeichenbar sind.

(Die "Zähflüssigkeit" wäre einer eigenen interessanten Untersuchung wert - und erinnert mich ein wenig an sogenannte "Wellenmaschinen", bei die Punkte sich auch nicht einzeln bewegen, sondern voneinander "mitgerissen" und gleichzeitig "in Zaum gehalten" werden:

 

[vgl. , wobei allerdings eine echte, also mechanische Wellenmaschine   allemal viel aussagekräftiger ist] )

Mit solchen Kurvenlinealen bekommt man vielleicht überhaupt erst ein "Gefühl" für schmiegsame Funktionsgraphen - und lassen sich schön alle gängigen Funktionstypen "nachschmiegen", also z.B.

• 
  Funktionsgraph zweiter Ordnung (Parabel)
• 
  Funktionsgraph dritter Ordnung,
• 
  Funktionsgraph vierter Ordnung,
• 
  Funktionsgraph des Sinus.

Der Vorteil dieser Kurvenlineale gegenüber jeder festen Schablone à la ist dabei die - im doppelten Sinne - Flexibilität:

1. die Biegsamkeit,
2. damit aber auch ein vielfältiger Einsatz: z.B. kann man mit solchen biegsamen Kurvenlinealen sehr schön und leicht Streckungen und Stauchungen durchführen.

Kurvenlineale gehören also in allen Unterrichtseinheiten zu Funktionsgraphen - ganz entgegen bisherigem Usus - in jede Schulklasse, und falls die Anschaffung für alle EinzelschülerInnen zu teuer ist, kann man sich auch mit einer Süßigkeit helfen, die manchmal auch "Meterkabel" genannt wird:

Vorsicht: SchülerInnen machen (erwartungsgemäß!) mit Kurvenlinealen erstmal nichts (mathematisch) Sinnvolles, sondern "verschwurbeln" und verknoten sie, bis sie brechen!

Und weitere Alternativen:

ein biegsamer Bleistift und ein biegsames Radiergummi

,

beide - nebenbei gesagt - gekauft im Museumsladen des Dogenpalastes in Venedig!

Und ideal für den Unterricht sind  

Rohrreinigungsspiralen

mit bis zu 10 m Länge!

Mit all dem ist aber noch nicht geklärt, weshalb gewisse Kurven (Funktionsgraphen) schön sind - wenn das nicht sowieso rein subjektiv ist

(aber gegen die windelweiche Pseudotoleranz der Banausen und kulturellen Allesfresser ist mir manchmal sehr danach zu behaupten, dass eben nicht "alles Geschmackssache" ist).

Kriterien für die Schönheit von Kurven scheinen mir zu sein:

1. Stetigkeit, dass sie also mit einem einzigen Strich durchgezeichnet werden können und somit keine Sprünge haben,
2. Differenzierbarkeit, dass sie also keine Spitzen haben

(Auf die Gefahr hin, [vermeintlich] sexistisch zu werden: eine Hängebusen oder ein Bierbauch, der Falten wirft, ist nicht differenzierbar.)

Aber das reicht noch nicht für Schönheit, denn die typische Schüler-Skizze wie

(vgl. )

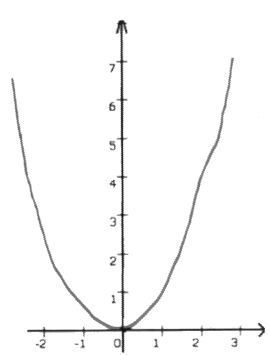
ist zwar sowohl stetig als auch differenzierbar

(und - gar nicht so selbstverständlich - tatsächlich ein Funktionsgraph, also nirgends senkrecht oder rückläufig),

aber eben doch unschön, weil sie zu "zackelig" ist, d.h. keine klaren "Trends" hat. Schauen wir uns das genauer an übersichtlicheren Kurvenlineal-Beispielen an:

1. :
   hier ist unschön, dass die Kurve weitgehend eine Links-, im rot markierten Bereich aber kurzfristig eine Links-, eine Rechts- und dann wieder eine Linkskurve ist.

Wohlgemerkt: das ist erstmal eine ästhetische Feststellung - aber auch mathematisch bedeutsam: eine Parabel ist immer entweder eine Links- oder aber eine Rechtskurve, aber nicht abwechselnd das eine und das andere.

2. :

hier liegt zwar (mathematisch korrekt) durchgehend eine Linkskurve vor, aber dennoch wirkt der Graph noch nicht schön, weil er im rot markierten Bereich einen unschönen Knick hat:

wenn man von links oben kommt, gilt fürdie Steigung (!) des Graphen:

• anfangs ist fast gleichmüßig,

• am Knick ändert sie sich rapide,

• danach bleibt sie wieder erstmal gleichmüßig,

• und erst im orangen Bereich ändert sie sich schön kontinuierlich.

Nochmals wohlgemerkt: auch in diesem Fall  wurde erstmal rein ästhetisch argumentiert - aber das ist wieder auch mathematisch bedeutsam: die Steigung einer Parabel ändert sich kontinuierlich (sogar linear) und nicht abrupt.

Die Steigung wird aber in der Mathematik mittels der Ableitung gemessen, so dass ich die These wage:

3. wird eine mathematische Kurve als schön empfunden, wenn auch der Graph ihrer Ableitung schön ist, womit die Ableitung einen ganz neuen, nämlich auch ästhetischen Wert gewinnt.

Erst Monate später lese ich zufällig dazu:

"Das menschliche Auge nimmt keine Unstetigkeiten (»Spitzen«) in der Krümmung, d.h. der zweiten Ableitung, wahr. Also werden zweimal stetig differenzierbare, kubische Splines als »glatt« wahrgenommen."
(Quelle:   )

(Dem Malermeister, der unseren Flur angestrichen hat, sind auch mehrfach Fast- Knicke unterlaufen: er hatte einfach kein "Auge" für geschwungene Linien, bzw. es ist auch gar nicht so einfach, sie mit Klebeband hinzukriegen:

)

PS:

1. Besonders schöne und mathematisch bedeutsame Kurven gibt's im " Famous Curves Index". 

2. Vgl. auch .
3. Schöne Kurven sind insbesondere auch die sogenannten Lissajous-Figuren wie z.B.