Vgl. auch "Am 1.1.1801 entdeckt Guiseppe Piazzi in Palermo einen neuen Planeten im Sternbild Stier, den er Ceres Ferdinandea nennt. Schon lange hatten die Astronomen in der großen Lücke zwischen Mars und Jupiter einen weiteren Hauptplaneten vermutet, und die Ceres schien dieser gesuchte Planet zu sein. Piazzi kann den neuen Planeten, unterbrochen durch schlechtes Wetter, jedoch nur wenige Wochen verfolgen. Die letzte Beobachtung gelingt am 11. Februar, dann verschwindet der Planet hinter der Sonne. [...] Im Oktober 1801 erhält Carl Friedrich Gauß (1777-1855), damals Privatgelehrter in Braunschweig, die Beobachtungsdaten von Piazzi. Er entwickelt daraufhin eine neue Methode der Bahnberechnung aus nur wenigen Beobachtungen, berechnet damit die Bahn der Ceres und ferner ihre Bewegung am Himmel für den Monat Dezember. Aufgrund dieser Berechnungen finden Franz Xaver Freiherr von Zach in Gotha am 7. Dezember 1801 und Wilhelm Olbers in Bremen am 1. Januar 1802 den neuen Planeten sehr nahe dem vorausberechneten Ort im Sternbild Jungfrau wieder. Der damals 24-jährige Gauß, bereits berühmt als Mathematiker, wird mit dieser Bahnberechnung mit einem Schlage auch unter den Astronomen weltbekannt. Nicht zuletzt diese Berechnungen führten später dann zu seiner Berufung als Direktor der Sternwarte nach Göttingen." (zitiert nach ; vgl. auch )

Vorweg: es stört mich ja sowieso, dass Kurven im Mathematikunterricht meist in fertigem Zustand statt auch mal in langsamer Entstehung (von links nach rechts) durchgenommen werden.

In sind die beiden Kurven 1 und 2 schon fertig gezeichnet, während von der Kurve 3 bislang nur der Anfang gezeigt ist. Wie also könnte diese Kurve 3 sinnvoll weiter gehen?

"Sinnvoll" soll dabei heißen, dass der bisherige "Trend", wie er sich in  den Kurven 1 und 2 andeutet, fortgesetzt werden soll.

Nun sehen die beiden Kurven 1 und 2 auf den ersten Blick beide annähernd wie Kreissegmente aus

,

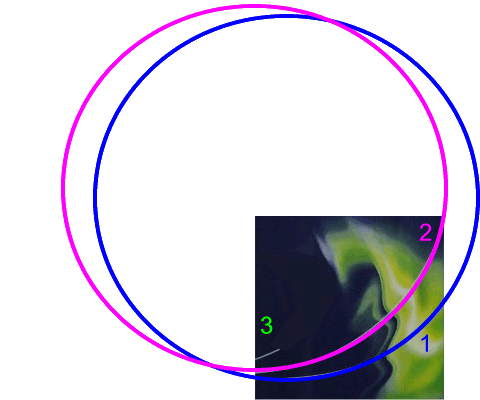weshalb es naheliegt, auch die Kurve 3 als Kreissegment darzustellen:

Damit ergäbe sich:

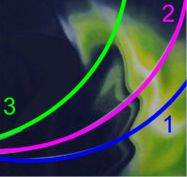
(Ein Nachteil der Konstruktion ist allerdings, dass anfangs von der Kurve 3 so wenig zu sehen war, dass jeder Versuch, einen passenden Vollkreis einzuzeichnen, nur sehr ungenau sein kann.)

Das Ergebnis ist offensichtlich abhängig von der Vorentscheidung, in den fertigen Kurven 1 und 2 Kreissegmente sehen zu wollen.

(Eine - wie der Fall Kepler zeigt - evtl. fatale Vorentscheidung, die blind gegenüber allen [evtl. sinnvolleren] Alternativen machen kann.)

Und mir scheint auch noch eine andere, typische Mathematiker-Vorentscheidung eingegangen zu sein: die Kurve 3 darf nicht senkrecht oder gar rückläufig werden, da dann keine Funktion mehr vorläge.

Eine anderer denkbarer Verlauf von Kurve 3 ergibt sich nämlich, wenn man zusätzlich eine "Zwischenkurve" 2a zeichnet: 

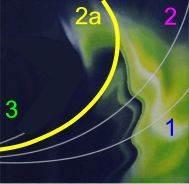
Und daraus dann ergibt sich die folgende Variante der Kurve 3:

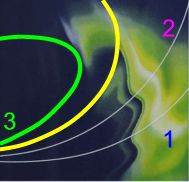
Nun erst sei die Herkunft bzw. das Geheimnis des anfänglichen Bildes gelüftet: ursprünglich steht es (mit vollständiger Kurve 3) auf einer Haarwaschmittel-Flasche:

(Ach, ist dieses Werbedeutsch nicht herrlich bescheuert? - was man aber vielleicht erst bemerkt, wenn man es in den Alltag übersetzt. Man stelle sich also mal vor, meine Frau fragt mich, was ich vorhabe, und ich antworte: "Ich verleihe meinem Haar jetzt mal auf die Schnelle einen Frische-Kick mit meinem For Men Shampoo".) 

Die Variante , in der ein bestehender Trend nur unverändert fortgesetzt wird, wäre wohl auch viel zu un-dynamisch für ein Haarwaschmittel, das angeblich einen "Frische-Kick" liefert. Dynamisch hingegen ist es hingegen, wenn - wie in -

Halten wir es nochmals als "Erkenntnisprinzip" fest, dass 

Gegeben seien in einem zweiten Beispiel eine fertige Kurve 1 und eine halbfertige, noch zu vervollständigende Kurve 2:

Hier liegt wohl als Vervollständigung der Kurve 2 nahe:

(Ein "richtiger" Mathematiker wird bei der Reihenfolge Kreis/Ellipse wohl schon etwas ahnen, was hier allerdings noch nicht verraten sei.)

Vielmehr fragen wir uns, wie der Ansatz einer Kurve 3

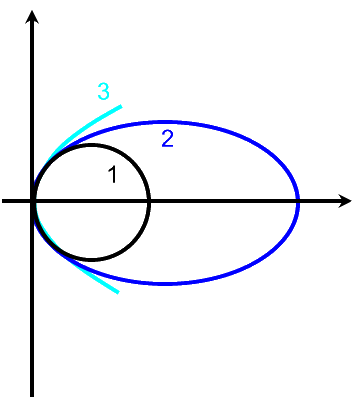
weiter verlaufen könnte.

Eine erste Möglichkeit wäre natürlich, dem Trend sklavisch zu folgen und wieder eine (noch größere) Ellipse zu zeichnen:

... und so dann in alle Ewigkeit (nur immer größere) langweilige (?) Ellipsen.

Oder man wagt

(unter Beibehaltung eines Teils des Trends, nämlich immer größerer Öffnung)

Neues, nämlich eine Kurve 3, die sich rechts nicht mehr schließt, sondern sogar immer weiter ansteigt:

Dabei ist die Kurve 3 eine Parabel, und - das sei hier schnell verraten - als nächste Kurve 4 ergibt sich eine Hyperbel:

Und jetzt sei eben doch endlich verraten, was ein "richtiger" Mathematiker längst geahnt haben wird, nämlich dass hier mit Kreis, Ellipse, Parabel und Hyperbel die klassischen vier Kegelschnitte vorliegen:

Diese Kegelschnitte mögen als netter Gag wirken. Viel interessanter ist aber, dass die vier Figuren auch die möglichen Flugbahnen von Weltraumobjekten (Planeten, Satelliten, Kometen ...) sind:

• Kreis und Ellipse bedeuten, dass solch ein Gegenstand regelmäßig wiederkehrt, also vom Bahnzentrum eingefangen wurde (vgl. die Planeten, erdumkreisende Satelliten oder regelmäßig wiederkehrende Kometen),
• Parabel und Hyperbel hingegen sind Flugbahnen von Objekten, die aus dem Unendlichen kommen und ohne Wiederkehr auch dorthin  zurückkehren, bei denen es die Gravitation des Bahnzentrums es also zwar geschafft hat, sie kurzzeitig  abzulenken, aber eben  nicht, sie einzufangen.

Und da haben wir dann mal mitten im Matheunterricht endlich mal astronomische Anwendungen, die in der Schule üblicherweise leider viel zu kurz kommen. 

Ein drittes Beispiel, das ganz ähnlich anfängt wie das zweite:

Überlegen wir uns, welche Möglichkeiten für den weiteren Verlauf der Kurve 2 da noch "drin" sind:

1. - und wie schon im zweiten Beispiel bei der Ellipse - eine Rückkehr der Kurve 2 zur x-Achse:

2. , dass die Kurve 2 wie der Logarithmus immer weiter und gleichzeitig doch immer schwächer wächst:

3.  , dass die Kurve 2 zwar immer weiter wächst, aber immer näher gegen eine Asymptote - - - kommt, die trotz ewigen Wachsens nie geschnitten oder gar überschritten wird:

4. , dass die Kurve 2 exakt parallel zur x-Achse wird:

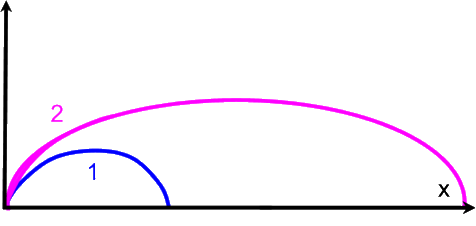
Angenommen mal, wir wählen tatsächlich diesen 4. Fall der Parallelität. Wie sieht dann die Verlängerung der Kurve 3 aus?:

Nach

• Rückkehr zur x-Achse,
• Parallelität zur x-Achse

scheint mir jetzt logisch "ewiges Steigen" zu folgen:

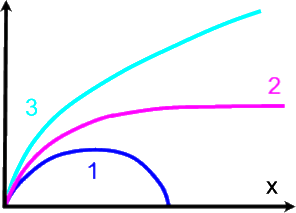
Bemerkenswert ist aber, dass auch dieser Graph aus einem astronomischen Zusammenhang stammt, nämlich aus dem Buch

Und dort sieht der Graph so aus:

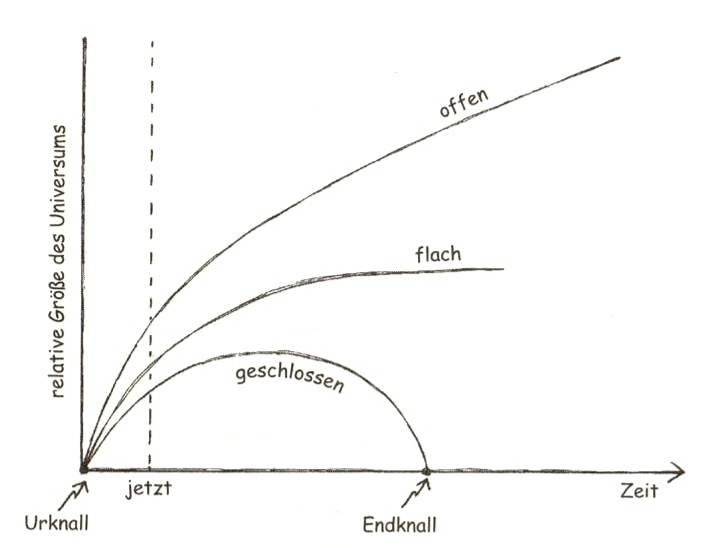
Gemeint damit ist Folgendes:

1. : wenn (falls ich es richtig verstanden habe) die "kritische Masse" des Universums zu groß ist, ist dieses "geschlossen" und kollabiert es nach langer Zeit wieder in einem Endknall; es ist wie ein Luftballon, der erst aufgeblasen wird und aus dem dann nach und nach die Luft wieder entweicht;
2. : wenn die "kritische Masse" des Universums "genau richtig" ist (und dafür scheint vieles zu sprechen), hält die Ausdehnung des Universums irgendwann einfach an, expandiert es also nicht weiter, kollabiert es aber auch nicht; das Universum ist dann "flach";
3. : wenn die "kritische Masse" des Universums zu klein ist, nennt man es "offen" und wird es in alle Ewigkeit weiter expandieren.

(Vgl. )