Mathematik verstehen 1

Jetzt, nachdem ich frühpensioniert bin, gebe ich vermehrt Nachhilfe

(vgl. ), 

und zwar

1. einigen Schülern kontinuierlich,
2. einigen Schülern

(meinem in Sachen Schule unwilligen Sohn sowie Kindern von Freunden und Bekannten)

immer nur "kurz vor knapp" bzw. "auf den allerletzten Drücker", also am besten am letzten Tag vor einer Klassenarbeit, wenn plötzlich Panik sogar die Faulsten oder Desinteressiertesten aufschreckt.

Das Wort "Nachhilfe" impliziert, dass da immer dem Unterricht hinterher(!)gehechelt wird, und zwar auch im ersten Fall

(kontinuierliche Nachhilfe, aber meistens doch nur einmal pro Woche):

über eine Hausaufgabenhilfe kommt man da kaum hinaus, denn (unverstandene) Hausaufgaben stehen immer an.

Und wenn im zweiten Fall nur einige wenige Nachhilfestunden direkt vor einer Klassenarbeit stattfinden, kann man eh nur versuchen, nach(!)träglich die allerwichtigsten Rechenverfahren einzubläuen, die Schüler brauchen, um immerhin noch eine mittelprächtige Note in der Klassenarbeit zu erreichen.

Von (tieferem) "Verständnis" kann also in beiden Fällen kaum die Rede sein

(und oftmals eben auch nicht in dem Unterricht, dem da nachgeholfen werden soll).

Wegen meiner Nachhilfestunden bin ich von einer ungenannten Person

(Nicht-Mathematiker)

mehrfach dringlich gebeten worden,

• mich nicht noch kurz vor Toresschluss um "Verständnis" zu kümmern,
• sondern "einfach nur" die wichtigsten Rechenverfahren einzupauken

(und vielleicht hatte die Person damit ja sogar recht).

Das hörte sich oft so an, als sei

• das Verstehen sowieso

(also auch unabhängig von anstehenden Klassenarbeiten)

unnötiger Luxus bzw. verlorene Liebesmüh'

• und allein die Beherrschung von Rechenverfahren wichtig

(wobei noch immer "Mathematik = Rechnen" unterstellt wird; vgl. ).

Auch viele Schüler denken so, und zwar nicht nur direkt vor Klassenarbeiten, sondern auch ganz allgemein über Matheunterricht:

• das Verstehen haben sie völlig resigniert längst aufgegeben

("ich versteh' gar nix mehr" bzw. "ich versteh' das alles nicht"),

• bzw. weil Mathe sie nicht interessiert, wollen sie auch gar nicht mehr verstehen, sondern nur halbwegs mit der Beherrschung von Rechenverfahren "durchkommen"

(wo sie nunmal schon Mathematik betreiben müssen).

Und gerade die Bienenfleißigen

(die "-Mädchen", die auch nicht an Mathematik, wohl aber an guten Zensuren interessiert sind)

bestehen oftmals auf der Vermittlung eines "Schema F": sie haben nur allzu gut begriffen, was heutzutage wirklich zählt.

Kleines Intermezzo zu "ich versteh' gar nix mehr" bzw. "ich versteh' das alles nicht": ein Eindruck bei Schülern, der beispielsweise bei der Aufgabe

"Vereinfache !"

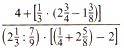aufkommen mag.

Weil in dieser Formel

(unnötigerweise, also aus Ignoranz oder Bosheit; Lehrer mögen immer bedenken, dass sie "sowas" auch ungerne rechnen)

sämtliche Schweinereien dieser Welt eingebaut sind, ist sie allemal kompliziert, so dass sie auch schön ín einem (Pseudo-)Mathematikfilm im Hintergrund auf einer Tafel auftauchen könnte:

(aus der Serie )

Da denkt sich doch jeder ehrfürchtig: "Das können doch nur Mathegenies lösen [aber ich nicht]."

Nun ist der Befehl "Vereinfache!"

(das freundlichere "Vereinfache bitte!" wäre wohl verlogen, weil die Schüler es ja vereinfachen müssen)

immerhin auch das Versprechen, dass 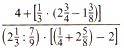tatsächlich einfacher gemacht werden kann.

Wenn die Schüler nun aber 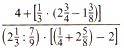vereinfachen müssen, fangen viele überall gleichzeitig an

(und machen es dadurch oftmals nur noch komplizierter; oder es wird gnadenlos vereinfacht, denn wirklich einfach ist nur 1).

Viel besser wäre es aber, wenn die Schüler den Term 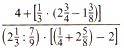vor jeder Rechnung erstmal langsam verstehen (!) würden, indem sie

• sich anfangs all die eingebauten Schwierigkeiten

("dies kann ich nicht - und das kann ich nicht - und jenes kann ich nicht")

klar machen würden:

1. Brüche und (noch schlimmer) gemischte Zahlen,
2. ein großer Bruch und viele kleine, die alle an dem großen "dranhängen": ,

(womit schon klar ist: den großen Bruch erledigen wir, falls möglich, erst ganz am Ende),

3. Bruchdivision,
4. Klammern und (noch schlimmer) Klammern in Klammern,
5. Produkt von Klammern,

(ich würde jedem Schüler einige Punkte zuschustern, der nur diese Schwierigkeiten benennt, aber nicht rechnen kann),

• die fein säuberlich herausgearbeiteten Schwierigkeiten einzeln angehen würden

(und den vorerst unbearbeiteten großen Rest unverändert neu aufschreiben würden),

• vom Kleinen (Überschaubaren) sukzessive zum Großen (vorerst allzu Komplizierten) übergehen würden: .

Wieso betreibt man dann überhaupt Mathematik?!

(Nunja, nochmals: Mathematik ist in der Schule ein Zwangsfach.)

Wolfgang Meyerhöfer war nicht der erste, der Dyskalkulie für eine "erfundene Krankheit" gehalten hat

(sondern vgl. etwa auch ).

Aber er hat es doch schön auf den Punkt gebracht:

(Quelle: ).

(Meyerhöfer bezieht sich wohl vor allem auf die Grundschulmathematik: da habe ich [zu?] wenig Ahnung von - weshalb mein Respekt vor Grundschullehrern nur um so größer ist: es scheint mir fast ein Leichtes, Schülern, die schon die Grundrechenarten beherrschen, auch noch das bisschen Gymnasialmathematik beizubringen. Aber wie vermittelt man die ersten und damit gewaltigsten Abstraktionen, nämlich die Grundrechenarten?)

Wichtig an Meyerhöfers Äußerung ist mir aber nicht das Thema Dyskalkulie, sondern dass Meyerhöfer dem puren (unverstandenen) Rechenmechanismus eine Absage zugunsten des Verstehens gibt:

Ein schönes Beispiel ist da die Bruchrechnung:

• man kann gar nicht genug Zeit in das Grundverständnis von Brüchen "investieren",
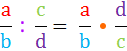• auch wenn später beispielsweise die Bruchdivision völlig abstrakt ist und überhaupt Rechnungen wie 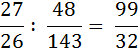ohne jede Anschauung einfach nach Schema F abgearbeitet werden.

Wenn man hingegen gleich zu den abstrakten Bruchrechenregeln

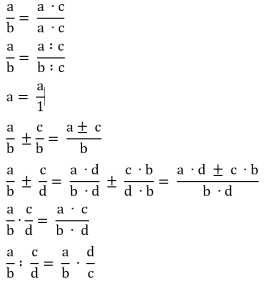
kommt

(und sie in massenhaft Aufgaben üben lässt),

scheitert doch oftmals alles am fehlenden Grundverständnis:

• da wissen Schüler z.B. nicht, dass der Bruchstrich eine andere Schreibweise für ein Divisionszeichen ist, und deshalb können sie nichtmal = 3 rechnen;
• oder die Schüler haben nicht das mindeste Verständnis für die Vorteile der Brüche gegenüber den

(von Taschenrechnern ausgespuckten)

Dezimalzahlen, also z.B.

•       0,142857142857142857142857142857... = ,
• 7 • 0,142857142857142857142857142857... = ???
• 7 • = 1 !!!

Besonders wichtig scheinen mir dabei

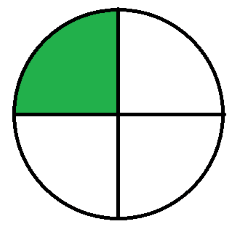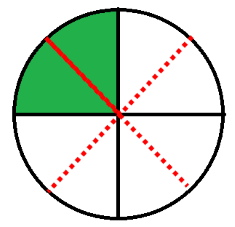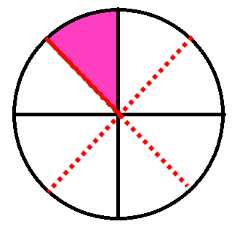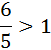• anschauliche Grundvorstellungen: z.B.
  • bedeutet das "mal" in ein "von" und somit "eine Hälfte von einem Viertel"
  ,
  • wenn man viele Teile noch weiter zerkleinert, werden es noch mehr Teile,
• das Abschätzen von Brüchen, also z.B. und ,
• Überschlagsrechnungen, also z.B.

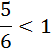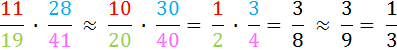
(denn das korrekte Ergebnis = ≈ 0,395378690629011553273427471116816 ist doch so oder so unvorstellbar:

• in der Bruchschreibweise: da werden 308 Kuchen auf 779 Personen verteilt???

• und sowieso in der Endlos-Dezimalschreibweise 0,395378690629011553273427471116816...).

(So ganz stimmt es aber nicht, dass das Verstehen vor dem Rechnen erfolgen muss: häufig kommt der Appetit erst beim Essen, will heißen: wenn man einen Mechanismus massenhaft stumpf angewandt hat, ergibt sich oftmals ganz nebenbei und fast unbemerkt eben doch ein Verständnis.)

In Nachhilfestunden kurz vor Klassenarbeiten mag tatsächlich keine Zeit mehr für (tieferes) Verständnis sein. Ansonsten aber bin ich der nostalgischen oder gar reaktionären Ansicht,

Ich glaube also fest, dass

• besser die Schulmathematik beherrscht

(also auch - ganz pragmatisch gesehen - bessere Schulnoten in Mathematik einheimst),

• wer versteht, was er tut, statt nur eingepaukte Verfahren abzuspulen

(was meist schon bei der kleinsten Variation der Aufgabenstellung schiefgeht - und nach wenigen Wochen schon wieder vergessen ist).

Aber

• das ist immer noch von den Rechenschemata aus gedacht, die oftmals den Standardunterricht und in Folge davon auch die Klassenarbeiten beherrschen,
• bzw. Verständnis ist da nach wie vor nur Mittel zum Zweck des stumpfen Rechnens.

In Wirklichkeit ist es aber genau umgekehrt:

• "richtige" Mathematik ist Verstehen,
• und Rechnen ist da höchstens Abfallprodukt bzw. Mittel zum höheren Zweck des Verstehens

(viele Mathematiker hassen oder verachten ja das Rechnen; vgl. ).

Nicht das Rechnen, sondern Beweise sind "das Herz der Mathematik" . Aber was ist ein Beweis denn anderes als der Versuch zu verstehen, weshalb ein (neuer) mathematischer Sachverhalt gilt?!

(Vielleicht bedeutet "Verstehen" ja wirklich,

• etwas Neues, Unbekanntes
• an bereits Bekanntes, Gesichertes anzuknüpfen.

Nebenbei: es gibt eine interessante Ausnahme vom Beweisbedürfnis:

Srinivasa Ramanujan
[*1887 +1920],

ein indischer Autodidakt, der es alleine bis in die abstraktesten Höhen der Mathematik geschafft hat,

• wusste einfach, dass ihm seine mathematischen Entdeckungen von der Göttin Namagiri in seinen Träumen eingegeben wurden und damit [weil göttlichen Ursprungs] automatisch richtig [bewiesen] waren,

• und verspürte deshalb nicht das geringste [sonstige] Beweisbedürfnis.)