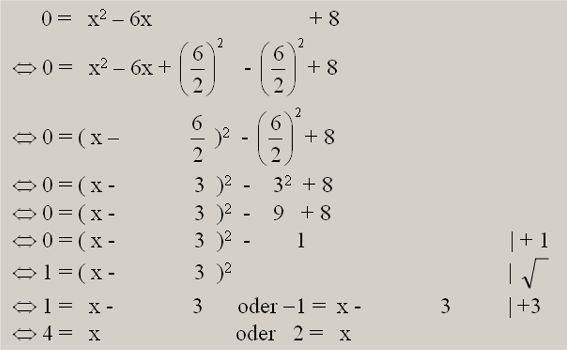wie man Mathearbeiten schreibt

Im Folgenden ist von Standard-Mathearbeiten die Rede: da mag es Ausnahmen geben - und sicherlich Variationen:

• Mathearbeiten gehen den Stoff in derselben Fachsystematik durch wie der Vorunterricht. Beispielsweise kommt da (in einer 10. Klasse) garantiert der Sinus vor dem Cosinus.

• Mathearbeiten gehen den Stoff von "leicht" nach "schwer" durch, d.h.

  • die erste Aufgabe dient netterweise zum "Warmlaufen", d.h. sie ist üblicherweise so angelegt, dass sogar die leistungsschwächsten SchülerInnen sie noch können, damit sie erstmal Sicherheit gewinnen.

• Die letzte Aufgabe verlangt einen Transfer, d.h. man kann sie zwar mit den im Unterricht durchgenommenen Mitteln lösen, braucht aber doch noch ein wenig eigenen Gehirnschmalz dazu.

Oftmals dient diese letzte Aufgabe auch dazu, schon zum Stoff überzuleiten, der nach der betreffenden Klassenarbeit im Unterricht ansteht.

Man nennt diese letzte Aufgabe auch "Einser-Aufgabe": wer diese letzte Aufgabe nicht löst, kann keine "Eins" mehr bekommen - aber immerhin in der Regel noch ein "gut".

Anders gesagt: es ist wahrhaft kein Beinbruch, wenn man die letzte Aufgabe nicht lösen kann.

• Es gibt

  • grobe Unterschiede zwischen den Hauptaufgaben (also zwischen 1., 2., 3. ...),

  • feine Unterschiede zwischen den Teilaufgaben (also z.B. zwischen 1a., 1b. 1c. ...)

  Beispielsweise handelt dann

  • Aufgabe 1 (mit allen Unteraufgaben 1a., 1b., 1c. ...) vom Sinus,

  • Aufgabe 2 (mit allen Unteraufgaben 2a., 2b., 2c. ...) vom Cosinus

  • ...

  Aber

  • 1a. wird eine noch ganz einfache Aufgabe zum Sinus sein,

  • während 1b., 1c. ... zunehmend schwierigere Aufgaben, aber alle noch zum Sinus sind.

• Man sollte also (wie auch bei Klassenarbeiten in anderen Fächern) niemals sofort loslegen, sondern sich erst mal umschauen. Es ist also äußerst ratsam, während einer Mathearbeit nicht sofort loszurechnen, sondern sich

1. zumindest alle Teilaufgaben (z.B. 1a., 1b., 1c. ...) einer Hauptaufgabe (hier 1.)

2. oder sogar erst die Gesamtarbeit (1., 2., 3. ...)

anzusehen.

Und dazu bedarf es eines "Parser"-Blicks: ein "Parser" ist ein Computerprogramm, das mathematische Ausdrücke (z.B. Terme) auf ihre speziellen Eigenarten hin untersuchen kann. Solch ein "Parser" erkennt also z.B., dass

• in 5(x+3) das Distributivgesetz angewandt werden muss,

• (3x - 4z)² mittels der zweiten binomischen Formel gelöst werden kann,

• 3•x²-7x ein quadratischer Term und der zugehörige Funktionsgraph gestreckt ist.

Wie dieser "Parser"-Blick angewandt werden kann, sei an einem Beispiel aus dem Schulbuch (dort S. 119) vorgeführt:

Das Buch ist hier relativ "nett", weil es

(das aber auch nur bei der ersten Anwendung des direkt vorher Gelernten)

• ansatzweise "verrät", was überhaupt zu tun ist: "Löse" bedeutet (im Gegensatz zu "forme um" oder "vereinfache"), dass nach dem bzw. den x gefragt ist, die die jeweiligen Gleichungen (!) lösen,

• mit "Bruchgleichungen", "Wurzelgleichungen" und "Biquadratische Gleichungen" "verrät", um welches Grundproblem es in den jeweiligen Aufgaben geht, also die Unterschiede zwischen den Aufgaben ausdrücklich nennt.

Solche "Nettigkeit" ist allerdings keineswegs üblich, und deshalb muss man die Unterschiede oftmals erst selbst herausfinden:

• in Aufgabe 1 und 2 besteht die Schwierigkeit in den Brüchen
  (genau genommen darin, dass Variable in Nennern auftauchen),

• in Aufgabe 3, 4 und 5 besteht die Schwierigkeit in den Wurzeln,

• in Aufgabe 6 geht es um biquadratische Gleichungen.

Der "Parser"-Blick sollte einem allerdings als Allererstes verraten

(und man sollte kurz überprüfen, ob da nicht doch irgendwo eine Ausnahme vorliegt),

dass in sämtlichen Aufgaben Gleichungen vorliegen, womit auch ohne ausdrückliche Nennung insgeheim "Löse" gemeint ist (s.o.) und der Lösungsweg garantiert immer folgendermaßen aussieht:

        Term 1 = Term 2

    Term 3 = Term 4

        ...     =     ....          (die Terme werden von oben nach unten immer einfacher)

    [ein] x  =     Zahl

(wobei hier davon abgesehen sei, dass

• verschiedene x Lösungen sein können,

• die vorliegenden Aufgaben erste Beispiele dafür sind, dass nicht mehr standardmäßig das Äquivalenzzeichen benutzt werden darf).

Anhand von Aufgabe 1 sei auch noch kurz untersucht, wo der Unterschied zwischen den Teilaufgaben (a, b, c ...) einer Hauptaufgabe (hier 1) besteht:

• in 1b taucht die Variable erstmals in zwei Nennern auf,

• in 1c taucht links zwischen den Brüchen ein Minus auf,

• in 1d tauchen zum ersten Mal Kombinationen in den Nennern auf (also x - 1 und x +2)

• ...

Wer aber diese nur scheinbar nebensächlichen kleinen Unterschiede nicht bemerkt, sieht auch nicht, wie das systematisch neue bzw. variierte Schwierigkeiten eingebaut sind, rechnet also alles gleich - und somit falsch.

Es gibt noch einen anderen Grund, vor allem Rechnen wenn schon nicht die gesamte Klassenarbeit, so doch zumindest alle Teilaufgaben einer Hauptaufgabe durchzulesen.

Gezeigt sei das - erstens - anhand eines "staatlichen" Vorschlags für sogenannte "Parallelarbeiten" in der 10. Klasse:

"[Ein] Dach [muss] neu gedeckt werden. Dazu werden rechteckige Dachziegel von 30 cm Breite und 40 cm Höhe verwendet.

1. Wegen der Dichtigkeit liegt jeder Dachziegel auf dem nächstfolgenden darunter liegenden ein Stück weit auf. Diese Überlappung macht 12,5 % der Ziegelfläche aus. Wieviel cm liegen die Ziegel demnach übereinander?

2. Jeder Dachziegel liegt auch auf seinem rechten »Nachbarn« 5 cm weit auf. Berechne, wie viele cm Dachfläche jeder Ziegel (außer am Rand des Daches) effektiv abdeckt."

Da ist es natürlich eine kleine Gemeinheit, dass erst in b. ganz unscheinbar die Antwort für a. auftaucht: "Jeder Dachziegel liegt auch auf seinem rechten »Nachbarn« 5 cm weit auf." D.h. doch, dass die Dachziegel sich auch horizontal - also in Aufgabe a. - um 5 cm überlappen.

(Nun muss man zwar das Ergebnis in a. noch herleiten, darf es also nicht einfach aus b. übernehmen, aber immerhin weiß man schon, was in a. rauskommen muss, nämlich 5cm.)

Ein zweites Beispiel, diesmal zu quadratischen Funktionen:

"a) Zeige, dass der Graph der Funktion y = x² -5x + 6,25 die x-Achse berührt.
 b) Zeichne den Funktionsgraphen von y = x² -5x + 6,25 in ein Koordinatensystem."

Wenn erst in b) nach der Zeichnung gefragt wird, kann "zeige" in a) nicht "zeichnen" bedeuten, ist in a) also wohl eine rechnerische Lösung gemeint.

• weitere Tipps für Klassenarbeiten:

• Man darf Klassenarbeiten in beliebiger Reihenfolge lösen, muss der Lehrkraft aber immer deutlich klarmachen, wo man gerade ist (Aufgabennummer).

• Wenn man eine angefangene Aufgabe woanders fortsetzt, muss man sehr deutlich machen, wo es weitergeht. Also z.B.:

  • „Fortsetzung auf der übernächsten Seite"

  • und auf der übernächsten Seite dann: „Fortsetzung von Aufgabe 3 b)".

Wenn die Lehrkraft eine Aufgabe oder deren Fortsetzung nicht findet, ist das nicht ihr Problem, sondern das der Schülerin/des Schülers.

• Es kann (insbesondere bei Loseblattordnern in der Oberstufe) sinnvoll sein, pro Aufgabe ein neues Blatt zu beginnen. Dann kann man später noch immer Nachträge anbringen. Wenn man aber derart mit losen Blättern arbeitet, wird man sich am Ende einer Klausur die Zeit nehmen müssen, die Blätter zu sortieren (am besten durchzunummerieren) und in richtiger Reihenfolge abzuheften.

• Bei sehr langen Termen und Gleichungen ist es manchmal ratsam, ein Blatt quer zu nehmen, damit der mathematische Ausdruck vollständig aufs Blatt passt und nicht durch eine Zeilentrennung unübersichtlich wird.

• Auch zu einer Mathearbeit (wie zu jeder Klassenarbeit) gehört eine gewisse Zeitplanung. D.h. insbesondere, dass man sich nicht allzu lange an einer Aufgabe "festbeißen" darf. Da stelle man sie lieber für einige Zeit zurück, löse erst mal andere Aufgaben - und komme dann später auf die Problemaufgabe zurück.
  überhaupt würde ich immer erst die Aufgaben rechnen, bei denen ich sicher bin, dass ich sie beherrsche.

• Es ist ratsam, Texte mit einem Füller zu schreiben, geometrische Zeichnungen aber mit einem Bleistift anzufertigen. Wenn einem nämlich eine Zeichnung noch nicht auf Anhieb gelingt, kann man sie dann immer noch schnell verbessern. Empfehlenswert ist es zudem, jede Zeichnung erst nur ganz dünn auszuführen und erst dann, wenn man sich ihrer sicher ist, deutlicher nachzuzeichnen oder z.B. auch verschiedene Elemente verschiedenfarbig zu zeichnen.

• Bei unübersichtlich langen Termen und Gleichungen ist es hilfreich, sich gleichartige und somit zusammenfassbare Elemente farbig zu markieren:

x² - 7x + 9 -3x² + 18 - 23x

 

Das hat zudem den Vorteil, dass man bei vielen Teiltermen keinen übersieht.

• Auf saubere Schrift achten: was die Lehrkraft nicht lesen kann, gilt als nicht geschrieben.

• Auf klare Unterscheidbarkeit achten: z.B. darf ein x nicht wie ein + aussehen

(all das macht man keineswegs nur der Lehrkraft zuliebe, sondern vor allem zum Selbstschutz: ich habe in meiner Schulzeit allzu oft falsch gerechnet, weil ich selbst nicht mehr mein x von meinem y unterscheiden konnte).

• Nach dem Abschreiben einer Aufgabe als allererstes überprüfen, ob man auch wirklich alles richtig abgeschrieben hat

(es ist doch einfach nur ärgerlich, wenn man mit einem Fehler anfängt und dann keinerlei Chance mehr hat).

• Aufgabenstellung genau lesen: was muss ich erledigen, was ist freiwillig?

• Man achte genau auf den Wortlaut der Aufgabenstellungen und da insbesondere auf die nur scheinbar unwichtigen Signalwörter.

(Ein Beispiel:

"Zeichne in jeweils ein Koordinatensystem die Funktionsgraphen der Funktionen

1. f(x) = - 3x +2,

2. g(x) = x²."

"jeweils ein" heißt ja wohl, dass

• in 1. ein Koordinatensystem zu zeichnen ist und in 2. ein zweites, neues,

• 1. und 2. also nicht in dasselbe Koordinatensystem gezeichnet werden sollen.

Und der Plural "FunktionsgraphEN" macht doch überdeutlich, dass zwei Graphen zu zeichnen sind, nämlich 1. derjenige von f und 2. derjenige von g.)

• MathelehrerInnen strukturieren manchmal

(in der [falschen?] Annahme, das sei besonders einfach)

überaus logisch, und diese Logik gilt es klar zu durchschauen.

(Beispiel sei da die soeben schon anzitierte, jetzt aber vollständige Aufgabe:

"a) Zeichne in jeweils ein Koordinatensystem die Funktionsgraphen der
     Funktionen

1. f(x) = - 3x +2,

2. g(x) = x².

 b) Erkläre anhand des Graphen von g, wie dem Wert x = 3 der zugehörige y-
     Wert zugeordnet wird."

Da bezieht sich die Aufgabenstellung in a) offensichtlich auf die Funktionen f in 1. und g in 2., während in b) nur noch von g aus 2. die Rede ist.

Und nebenbei: man achte hier auch wieder auf die Signalwörter "anhand des Graphen" in b): da wird offensichtlich eine zeichnerische, aber nicht eine rechnerische Herleitung erwartet.)

• Allgemeine Aufgaben wie z.B.

  • "Zeige, was eine Funktion ist!"

  (also die "Frage" nach der Definition von Funktionen, hier allerdings zweideutig gestellt, da ja nach "einer" [!] Funktion "gefragt" ist),

  • "Beweise den Satz des Pythagoras!"

  sind auch allgemein zu bearbeiten, d.h. da können einige konkrete Beispiele

  • zwar ein guter Hinweis sein, dass eine Aussage tatsächlich allgemein gelten könnte,

  • und auch deutlich machen, wie der allgemeine Beweis laufen könnte,

  aber konkrete Beispiele können den allgemeinen Beweis nicht ersetzen.

  (Merke: sobald ein einziger konkreter Zahlenwert eingesetzt wird, ist ein Beweis bzw. eine Definition nicht mehr allgemein.)

• Matheaufgaben sind meistens sehr suggestiv, d.h. sie geben oftmals die Antworten schon vor.

(Erstes Beispiel:

"Eine Pizza mit dem Radius 30 cm kostet 3 €, eine Pizza mit dem Radius 40 cm kostet 4 €. Bei welcher bekommt man mehr fürs Geld?"

Wenn einE MathelehrerIn schon so "blöd" fragt, ist doch wohl klar, dass falsch ist, was ein Laie denken könnte, nämlich dass man bei beiden Pizzas gleich viel fürs Geld bekommt.

Mathematisch ausgedrückt: das Verhältnis Preis/Pizzagröße ist nicht konstant.

 Zweites Beispiel:

"Entscheide, ob die gegebene Fläche endlich ist; schätze gegebenenfalls ihre Größe ab."

Da ist doch mit dem zweiten Teilsatz die Frage des ersten Teilsatzes fast schon beantwortet: Die Fläche lässt sich sowieso nur abschätzen, wenn sie endlich ist.)

• In Textaufgaben alle mathematischen Informationen unterstreichen und evtl. durchnummerieren; später überprüfen, ob man auch wirklich alle mathematischen Informationen benutzt hat. Bedenke: es gibt direkte (Zahlen) und indirekte (z.B. „genauso groß wie") mathematische Informationen.
  Ich selbst habe mir angewöhnt, in Analogie zur Ampel alles Bekannte grün und alles Unbekannte/Gesuchte rot anzustreichen.

• Meistens sind MathematiklehrerInnen insbesondere bei (scheinbaren) Anwendungsaufgaben so nett, nur die zur Rechnung wirklich nötigen, also keine überflüssigen oder doppelten Informationen zu geben. Daraus folgt aber, dass man zur Lösung der Aufgaben garantiert alle gegebenen Informationen braucht.

  (Ein Beispiel: Wenn die Aufgabe lautet

  "Die Eichmarke eines kegelförmigen Sektglases ist 10 cm hoch. Ein Barkeeper füllt jedoch nur bis 1,5 cm unter diese Marke. Wie viel Prozent des Sektes »spart« er dabei?",

  so ist zur Lösung dieses Problems offensichtlich die Breite des Sektglases unnötig bzw. wird trotz verschiedener Breiten immer derselbe Prozentsatz gespart.)

• Oftmals sind geometrische Informationen nur rein sprachlich gegeben. Dann zeichne man sich ein (zweidimensionales) Bild oder bastele sich sogar schnell einen (dreidimensionalen) Körper, um überhaupt eine Anschauung zu bekommen.

(Das ist keineswegs so utopisch, wie man meinen mag: Papier, Schere, ein Apfel [als Kugel] sowie Stricknadeln reichen.

Kleiner Tipp: bei dreidimensionalen Körpern

• erst solch einen dreidimensionalen Körper bauen

• und dann eine zweidimensionale Projektion davon zeichnen
  [in der man einige benötigte Hilfslinien oft leichter entdeckt].)

• Benötigte Formeln erstmal aufschreiben.

(Ein Beispiel: wenn ich (3x + 4)² umrechnen soll und erkannt habe, dass da die erste binomische Formel hilfreich ist, dann schreibe ich sie erst mal drunter:

(3x + 4)²

( a +  b)²,

womit immerhin schon mal klar ist, dass im vorliegenden Fall a = 3x und b = 4 ist.

Nun schreibe ich erst mal allgemein (a + b)² = a² + 2ab + b² und setze dann in a² + 2ab + b² wieder 3x und für b die 4 ein.)

• Es gibt ein „Gewohnheitsrecht" aus dem Unterricht: Aufgaben sind in aller Regel in genau der Form zu lösen, die im Unterricht üblich war.

• Besser einige Zwischenschritte zu viel als viele auf einmal und alles falsch.

(Auch Zwischenschritte mache man nicht der Lehrkraft zuliebe, sondern zum Selbstschutz:

• es weiß doch jeder, wie leicht er sich verrechnet, wenn er Mehreres "in einem Abwasch" versucht;

• angenommen,

  • eine Aufgabe besteht aus neun Zwischenschritten, die jeder mit einem Punkt bewertet werden

[und einen zehnten Punkt bekommt man, wenn man ausnahmslos alles richtig hat];

• man macht bei all den Zwischenschritten nur einen einzigen Fehler;

dann erhält man doch immerhin noch acht Punkte für die restlichen richtigen Zwischenschritte);

• Manchmal geben Mathelehrer "Tipps" zu Aufgaben, die zwar oft hilfreich sind, aber nicht befolgt werden müssen: evtl. führen auch ganz andere Wege als die in solchen Tipps vorgeschlagenen zum Ziel.

• Zwischenschritte sind auch wichtig, um der Lehrkraft zu zeigen, dass man selbst drauf gekommen ist und das Ergebnis nicht nur irgendwo "ermogelt" oder erraten hat.

• Es reicht also niemals das nackte Zahlenergebnis - und auf Fragen ist immer im Sinne der Frage in ganzen Sätzen zu antworten.

• Was man nur halb oder auch falsch gerechnet hat, streiche man erst dann  durch, wenn man eine ganze bzw. richtige Lösung hat, denn auch für Halbes gibt es Teilpunkte. Allerdings darf man nicht zwei Lösungswege gar noch mit verschiedenen Lösungen stehen lassen

(also nach dem Motto: "LiebeR LehrerIn, suche dir doch gefälligst selbst aus, was dir gefällt bzw. richtig ist").

• Wenn man etwas durchstreicht, dann bitte ordentlich (evtl. mit einem Lineal), nicht in wildem Gekrackel.

• Jede erledigte Teilaufgabe auf dem Aufgabenzettel abhaken, also z.B.

3a (erledigt)
  b (erledigt)
  c (noch nicht erledigt)

Erst wenn man alle Teilaufgaben erledigt hat, auch die Gesamtaufgabe abhaken, also z.B.

3a (erledigt)
  b (erledigt)
  c (erledigt), also (jetzt erst) Gesamtaufgabe erledigt.

• Vor Abgabe der Arbeit überprüfen, ob man alle Aufgaben abgehakt oder nicht vielleicht doch etwas übersehen hat.

• Wenn man noch Zeit hat: sämtliche Rechnungen nochmal durchlesen. Dann helfen einem besonders Ordnung und frühere Selbstkommentare

(z.B. | • 2 bedeutet dann: ich wollte beide ganzen Seiten mit 2 multiplizieren; habe ich es denn auch tatsächlich getan?).

• Auch wenn es Papierverschwendung zu sein scheint: immer untereinander rechnen:

  • Aufgabe 1a. hat nichts neben 1b. zu suchen

(dann ist der Bezug der Rand-Korrektur der Lehrkraft zur jeweiligen Aufgabe nicht mehr deutlich);

• möglichst auch alle Gleichungsumformungen untereinander ausführen, damit man selbst immer klar sieht, was man unverändert mitgeschleppt hat und was man an welcher Stelle verändert hat.

(Beispielsweise bei der quadratischen Ergänzung sieht das dann im Idealfall folgendermaßen aus:

.Daran kann man genau sehen,

• was von Schritt zu Schritt unverändert geblieben ist,

• wo Veränderungen stattgefunden haben

• und wie das Neue aus dem Alten hervorgegangen ist.)

• Leider ist es in der Mathematik oftmals unvermeidbar, dass man mit schwierigen Zahlen in den Aufgabenstellungen anfängt und daraus einfache Lösungen erhält - oder umgekehrt. Mir persönlich ist da die erste Möglichkeit lieber - und einfache Ergebnisse sind meistens ein gutes Kriterium für Richtigkeit.

• Damit SchülerInnen nicht meinen, dass alles nach einem Schema ablaufe, bauen MathelehrerInnen gerne Fallen ein, also z.B. mitten in quadratische Funktionen eine lineare Funktion oder mitten in lösbare Gleichungen plötzlich eine unlösbare Gleichung.

• Taschenrechner dürfen nicht weitergegeben werden

(denn damit kann man ja auch Ergebnisse weitergeben).

Wer also seinen Taschenrechner vergessen hat, muss alles "zu Fuß" rechnen.

• Klassenarbeiten gehören in ein Heft oder einen ordentlichen Ordner (mit Namen drauf!); „abgewrackte" Ordner und Loseblattsammlungen führen zu Punktabzug oder werden manchmal erst gar nicht angenommen.

• Der Rand des Klassenarbeitsheftes "gehört" der Lehrkraft.