Mathematiker können (fast) nichts

Es scheint mir ungeheuer wichtig, dass SchülerInnen erfahren, was üblicherweise nie im Unterricht gesagt wird:

Und dabei geht es keineswegs - was ja noch verständlich wäre - nur um hochkomplizierte Dinge, sondern es fängt bereits mit dem (nur scheinbar?) Allereinfachsten an:

1. MathematikerInnen können nicht einmal drei ganz einfache (kleine, natürliche) Zahlen gleichzeitig addieren, also z.B. 2 + 3 + 4 rechnen. Sondern sie müssen

• erst zwei der drei Zahlen addieren:
• um erst danach zu dem dabei entstehenden Zwischenergebnis die dritte Zahl addieren zu können:

2 + 3 + 4 = (2 + 3) + 4 =

                =     5     + 4 = 9 

Das einerseits so banale, andererseits (nur wegen des lateinischen Namens?) für SchülerInnen oftmals so schwierige "Assoziativgesetz" besagt dabei nichts anderes, als dass es egal ist, welche zwei der drei Zahlen man zuerst addiert:

(a + b) + c = a + (b + c)

(Man stelle sich mal vor, was es konkret bedeuten würde, wenn das Assoziativgesetz nicht gelten würde: man müsste beispielsweise im Supermarkt unterschiedlich viel bezahlen, je nachdem, in welcher Reihenfolge die Kassiererin die[selben] eingekauften Gegenstände einscannt.)

Schon an diesem ersten Beispiel wird klar:

Und sie sind sich auch nicht zu schade, die simpelsten Fundamente (Assoziativgesetz) abzusichern - und dann auf solch wirklich gesicherte Fundamente sukzessive gigantische Gebäude aufzubauen.

2. Und überhaupt können MathematikerInnen nur mit den allereinfachsten (ganzen) und zudem sehr kleinen Zahlen rechnen:

 "Malnehmen ist ein Kinderspiel. Wir lernen das schriftliche Multiplizieren in der Schule. Um das Produkt aus zwei beliebig großen Zahlen zu bilden, muss man nur [?] das kleine Einmaleins von 1 bis 9 beherrschen, der Rest ergibt sich, indem man die einzelnen Ergebnisse aufaddiert."
(zitiert nach "Die Zeit", 27.11.08)

Einer meiner Matheprofessoren im Studium sagte mal, rechnen täten wir eh nicht, und wenn, dann nur mit einfachen Beispielen, also den Zahlen 1 bis 10. Einen Taschenrechner bräuchten wir also nicht, und dementsprechend war er nach meinem Studium auch durch penetrantes Nichtbenutzen kaputt.

3.  

   „Die ganzen Zahlen hat der liebe Gott gemacht, alles andere [Brüche, irrationale Zahlen ...] ist Menschenwerk.“ (Leopold Kronecker)

Man mag es kaum glauben, aber MathematikerInnen können grundsätzlich nicht mit doch noch relativ simplen Brüchen rechnen, oder genauer: nicht direkt, sondern nur auf dem Umweg über die viel einfacheren ganzen Zahlen.

Z.B.

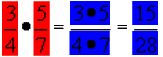
Es ist geradezu für die Mathematik typisch, was hier passiert:

... was man wohl "aus der Not eine Tugend machen" nennt.

Noch deutlicher wird das anhand der Bruchaddition, die merkwürdigerweise schwieriger als die Bruchmultiplikation ist, obwohl doch eigentlich die Addition einfacher als die Multiplikation ist

(worauf unten noch zurückzukommen sein wird):

Bemerkenswert daran ist aber auch, dass man sich vermutlich noch vorstellen kann, was und   ist

(3 Kuchen werden auf 4 Leute verteilt, also erhält jeder ein bisschen weniger als einen Kuchen;
5 Kuchen werden auf 7 Leute verteilt, also erhält jeder ein bisschen weniger als einen Kuchen;
bei der Addition erhält jeder also etwa 1,5 Kuchen),

während beim rechnerischen Ergebnis wohl jede direkte Vorstellung versagt.

Aber da machen die MathematikerInnen es sich nach all der Anstrengung einfach: der ungefähre Dezimalwert ≈ 1,4642857 interessiert sie doch nicht die Bohne

(ist ihnen mit all den Nachkommastellen viel zu kompliziert),

d.h. ihnen reicht das Rechengesetz (die Tätigkeit) und ist das Ergebnis (das fertige Produkt) egal.

4. Fast könnte man meinen, dass die MathematikerInnen masochistisch veranlagt sind: da können sie, wie in 2. gezeigt, schon kaum (direkt) mit Brüchen umgehen - und beschäftigen sie sich prompt mit noch komplizierteren, nämlich den sogenannten "irrationalen" (= unvernünftigen!) Zahlen wie z.B. , die sich eben dadurch "auszeichnen" (?), dass sie nicht mal als Brüche aus ganzen Zahlen schreibbar sind

(vgl. ).

"nicht mal als Brüche aus ganzen Zahlen schreibbar" bedeutet dabei auch, dass es nicht die mindeste Aussicht gibt, jemals den Dezimalwert von vollständig zu berechnen oder aufzuschreiben:

≈ 1,4142135623730950488016887242097 und so weiter und so unregelmäßig fort bis in alle Ewigkeit

(Einem Laien mag es sowieso herzhaft egal sein, wie diese Dezimalschreibweise weiergeht, bzw. mit - sagen wir mal - fünf Stellen nach dem Komma ist sie ihm doch allemal genau genug.)

Warum aber beschäftigen MathematikerInnen sich dann überhaupt mit solchen Zahlenmonstern?:

1. aus einem Vollständigkeitsbedürfnis: es "gibt" diese irrationalen Zahlen nunmal, bzw. so irrational sind sie anscheinend doch nicht;
2. so monströs sind sie in Mathematikeraugen gar nicht, sondern ganz im Gegenteil reizt ihre unvorhersehbare "Lebhaftigkeit" nach dem Komma.

Aber wie kommt man denn überhaupt auf ≈ 1,4142135623730950488016887242097? Irrationale Zahlen lassen sich zwar, wie bereits gesagt, nicht in Bruchform schreiben, aber immerhin doch beliebig genau durch Brüche annähern. Z.B.

• erste Näherung:    ≈ 1,4   =
• zweite Näherung:   ≈ 1,41 =
• ... 

Auch hier passiert wieder etwas für die Mathematik Typisches:

 Kommt hinzu, dass sich MathematikerInnen (wie schon oben bei ) doch nicht im mindestens für den scheußlichen Dezimalwert von interessieren - und dennoch prächtig mit rechnen können!

(Es ist wie mit hochtechnischen Geräten, die wir zwar nicht verstehen, aber doch wunderbar bedienen können.)

Denn da passiert doch etwas äußerst Merkwürdiges: obwohl in Dezimalschreibweise ein scheußliches Monstrum ist, ergibt die Multiplikation dieses scheußlichen Monstrums mit sich selbst erstaunlicherweise

(oder genauer: per Definition)

doch exakt 2 ohne jede Nachkommastelle:

( )² = 2 

Es ist, als ob die   sich bei Multiplikation mit sich selbst in einer Art Selbstmord auslöscht.

5. Es wird einen wohl kaum mehr wundern, dass MathematikerInnen auch mit Wurzeln nicht rechnen  können - oder zumindest nicht direkt. Vielmehr müssen sie auch das Rechnen mit Wurzeln (wie schon oben das mit Brüchen) auf das Rechnen mit simplen ganzen Zahlen zurückführen:

Bemerkenswert dabei ist (wieder), dass sowohl als auch in ihrer jeweiligen Dezimalschreibweise scheußlich irrationale Zahlen sind:

• ≈  1,41421356237309
• ≈  4,24264068711929

Zudem ist zumindest auf den ersten Blick keinerlei Ähnlichkeit zwischen den beiden Dezimalschreibweisen sichtbar. Und dennoch heben sie sich durch die Multiplikation gegenseitig zu einer glatten Zahl, nämlich 6, auf.

Und außerdem muss man die Zahlenwerte von und auch nicht im mindesten kennen - und kann dennoch zum Ergebnis 6 kommen.

6. Und - man wird es schon ahnen - Potenzen miteinander multiplizieren können die MathematikerInnen natürlich auch bzw. erst recht nicht (direkt)  - sondern führen sie wieder auf die Addition simpler ganzer Zahlen zurück.

2⁵ • 2⁷ = 2⁵⁺⁷ = 2⁹

Wichtiger als die ganzen Zahlen

(es geht auch mit anderen)

ist hier allerdings, dass eine komplizierte Multiplikation auf eine viel einfachere Addition zurückgeführt wird.

Das liegt - nebenbei gesagt - daran, dass

• die Potenzrechnung eine verkürzte Multiplikation ist:

3⁴ = 3 • 3 • 3 • 3

• und die Multiplikation wiederum eine verkürzte Addition ist:

3 • 5 = 3 + 3 + 3 + 3 + 3 ,

• also die Potenzrechnung letztlich eine extrem verkürzte Addition.

Dadurch hat die Potenzrechnung den Vorteil, kurz sehr große Zahlen darzustellen (z.B. 10⁸ = 100000000), aber eben auch den Nachteil, dass diese großen Zahlen schnell unvorstellbar sind.

Die Rückführung einer Multiplikation auf eine Addition (bzw. einer Division auf eine Subtraktion) wird aber insbesondere bei den Logarithmen (der Umkehrung der Potenzrechnung) hilfreich:

• zwar ist es gar nicht so einfach, die Logarithmen erstmal zu verstehen (ein Umweg!),
• wenn man sie aber erstmal verstanden hat, lassen sich mit ihnen Multiplikationen (und Divisionen) viel einfacher durchführen, nämlich auf einfachere Additionen (Subtraktionen) zurückführen

(was aber im Zeitalter des Taschenrechners kaum mehr nötig ist).

7. Wir hatten oben gesehen, dass Mathematiker in der Algebra mit kaum mehr als simplen ganzen Zahlen umgehen können.

Genauso stehts in der Geometrie, wo sie überhaupt nur mit geraden Gegenständen (Rechtecken, Quadraten, notfalls noch Dreiecken), aber grundsätzlich nicht mit krummen Gegenständen (Kreisen, Kugeln, Flächen unter krummen Graphen) umgehen können - oder zumindest nicht direkt.

Aber auch da benutzen sie den inzwischen uralten Trick, Unbekanntes (Krummes) auf dem Umweg über Einfacheres, Bekanntes (Gerades) anzunähern.

Vgl.