(Baumarkt-)Modelle

Warum in die Ferne schweifen,
wo der Baumarkt liegt so nah?!

Es ist doch so einfach:

• ein Knickstrohhalm verdeutlicht in der Vektorgeometrie eine Gerade:

mit dem Stützvektor kommt man auf die Gerade drauf, mit dem Richtungsvektor bewegt man sich in ihr (von Pusemuckel bis zur Autobahnauffahrt, und dann immer der Nase nach):

• zwei Knickstrohhalme verdeutlichen eine Ebene:

mit dem Stützvektor wieder auf die Ebene drauf, und die beiden Richtungsvektoren spannen dann die Ebene auf (man kann auf sie ein Blatt drauflegen):

Normalerweise ist ein "echtes", handgreifliches Modell immer einem Computerprogramm vorzuziehen.
Ich hab's beispielsweise im Filmmuseum Düsseldorf beobachtet: die heutzutage doch angeblich so virtualitätsversessenen SchülerInnen hatten erst richtig Spaß, wenn sie an einem Modell (z.B. einem Daumenkino) "rumpatschen" und rumfummeln konnten.

Es ist nachgerade schon "pervers" (lat. perversus "verdreht, verkehrt"), wenn

• letztens auf einer Tagung unter "den Klassenraum verlassen" nur ein virtuelles Verlassen ("Gang" durchs Internet bzw. computergestütztes Lernen von zu Hause aus; neudeutsch "e-learning") verstanden wurde;
• ein Computerprogramm in der Stochastik das Werfen von Heftzwecken simuliert - wo man doch Heftzwecken spottbillig in jedem Schreibwarengeschäft erwerben und dann hübsch (schmerzhaft?) mit ihnen rumwerfen kann.

Sinnvoll sind Computermodellierungen nur

1. , wenn nur mit ihnen etwas zeigbar ist, was ohne sie - also mit mechanischen Modellen - nicht geht (z.B. limitische übergänge),
2. , bei sehr großen (etwa statistischen) Datenmengen,
3. , wenn man beim besten Willen keinen Zeit für den umständlichen Modellbau hat (da ist es viel einfacher, eine CD einzuschmeißen und die Schüler mit Maus dran rumspielen zu lassen,
4. , wenn nach oder zur zentralen Erkenntnis Variationen nötig werden, die bei einer mechanischen Modelle eine komplette Umkonstruktion erfordern würden (beim "Integrator" unten z.B. zunehmend schmalere Stäbchen).

A) Modelle aus dem Baumarkt

"Warum in die Ferne schweifen, wo das Gute liegt so nah?"

Es ist wie mit Spielzeug für kleine Kinder: sie brauchen kein Fisher-Price und ähnlich sündhaft teure, oft nur eindimensional verwendbare "Spielzeuge", sondern oftmals reichen ganz normale alltägliche Gegenstände, z.B. Küchengeräte.

Genauso braucht man oftmals keine teuren expliziten Mathe-Modelle, sondern bediene sich im erstbesten Hobby- und Baumarkt, also z.B. mit den in ersteren erhältlichen Styroporkörpern: sie sind spottbillig, und deshalb kann man sie auch in Klassenstärke kaufen und dann durchsägen und durchbohren lassen. Hauptsache, die SchülerInnen nehmen etwas endlich mal auseinander, d.h. analysieren es.

Ab und zu gibt's aber in Baumärkten ganz besonders schöne Fundstücke, die wenn auch vielleicht nicht direkt verwendbar, so doch schöne Anregungen sind. Z.B.

1. ein "Parallelometer":

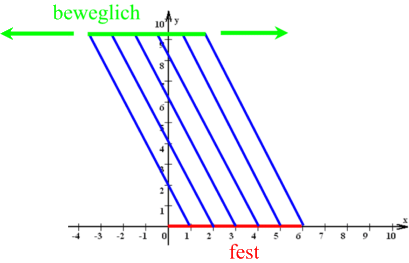
Das hier gezeigte Modell hat den Vorteil, dass man die Parallele wirklich "er-führt", also durch Bewegung (!) erzeugt. Die Trennung des Parallelen-Zeichengeräts vom Winkelmesser, also die Aufspaltung des Multifunktionsgerätes Geodreieck wieder in seine Einzelbestandteile finde ich sowieso - zumindest in der Anfangsphase - sehr sinnvoll (s.u.).
Dennoch scheint mir das vorliegende "Parallelometer" nicht direkt für den Unterricht geeignet, weil es allzu sehr mit Informationen überfüllt ist (schwer ablesbare Abstandsskala, trigonometrische Werte, Kalender!).

2. ein "Radiuszirkel":

Vorteil hier ist, dass der Radius direkt einstellbar und sichtbar ist, statt wie beim üblichen Zirkel zwischen den beiden Schenkeln nur virtuell zu sein.

3. ein "stumpfe-Winkel-Messgerät":

Dieser Winkelmesser beherrscht nebenbei aufgrund des Konstruktionsprinzips auch spitze Winkel.

Vor- und Nachteile des Modells halten sich die Waage:

• einerseits sind eben problemlos stumpfe Winkel (zwischen 180 und 2700) messbar, während beim üblichen Winkelmesser immer wieder die Gefahr besteht, dass die SchülerInnen "falschrum" ablesen und dann Winkel und Wechselwinkeln verwechseln;
• aufgrund der Konstruktion liegt die Messskala nicht direkt am eigentlich zu messenden Winkel, sondern ist mit ihm nur indirekt über ein Parallelogramm verbunden; die Funktionsweise ist also nicht ganz so offensichtlich, wenn auch aufgrund des einfachen Parallelogramms relativ einsehbar - und ermöglicht eine Einführung in Stufen-, Wechsel- und Ergänzungswinkel.

4. ein "Integrator"

(ursprünglich "Profilschablone", mit der man z.B. Ausschnitte im Parkett messen kann; auch bei der Kreisflächenmessung brauchbar),

hier probeweise auf Parabelform eingestellt:

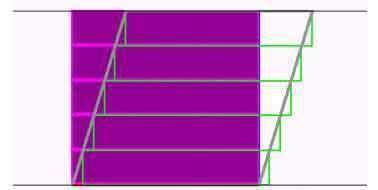
Interessant an diesem "Integrator"

(oder, um genauer zu sein, weil Fläche und Integral ja nicht identisch sein müssen: Flächenmessgerät)

ist vor allem die Konstruktionsprinzip (das ja im Grunde schon Newton "enthält"). Das Gerät in der vorliegenden Form ist hingegen wohl kaum im Unterricht brauchbar, weil die einzelnen parallelen Drähte mit 1 mm Breite viel zu dünn und somit ununterscheidbar sind.
Sinnvoller wäre wohl ein Großmodell mit 1 cm breiten Stäben, die zudem durchnummeriert und mit einer Zentimeterskala versehen sein könnten, so dass man sehr einfach die Höhe jedes Stabs ablesen könnte.

Und hier auch noch die "3D-Newton-Leibniz-Version":

5. Man wird auch anderweitig fündig:

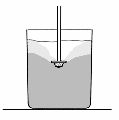
Milchaufschäumer zwecks simpelster Herstellung eines Rotationsparaboloiden in einem Wasserglas:

6. Oder warum in die Ferne schweifen, wo das Gute liegt so nah?: der in fast jedem Klassenraum vorhandene gute alte gibt in der Vektorgeometrie einen wunderbaren "Normalenvektor" zu einer Ebene ab, wobei der Kartenständer zudem den Vorteil hat, dass seine Füße in der Ebene liegen.

7. Und für Richtungsvektoren gibt's auch schöne Modelle:

• Teleskopkugelschreiber (evtl. inkl. Laserpointer, die die Geraden anzeigen):

• Angelruten:

8. ?

!

8. Kugeloberfläche und -volumen? Ja, wozu gibt's denn in jeder Schule einen Globus , auf dem praktischerweise auch schon die Breitengrade (Schichten) eingezeichnet sind?
   (Und mit den Längengraden ist man dann auch schon bei der nichteuklidischen Geometrie.)

9. Ist Ihre Schule auch so miserabel schlecht mit Mathemodellen ausgerüstet? Halten Sie die meisten käuflichen Modelle auch für total überteuert?
   Da empfiehlt sich Ihnen Ihr Bastelgeschäft:

auf dass kräftig gesäbelt werde!:

Es ist so ungeheuer wichtig, dass man die Dinge (gefahrlos) auseinander nehmen darf - sonst wird man, weil man nichts versteht, ja die Perfektion der Dinge einen beschämt, irgendwann nur noch gewalttätig destruktiv.

10. "das mitwachsende Prozentgummiband"

1. Das Band ist für alle Gefäße geeignet, deren Querschnitt sich vertikal nicht verändert (verjüngt).

2. Die Grundfläche kann jedoch sehr unterschiedlich sein (quadratisch, rechteckig, dreieckig, kreisförmig ...); es sind sogar schräge Gefäße möglich.
   (schon a. und b. sind besonders wichtig im Hinblick auf den relativen Anteil)

3. macht das Band wie kaum ein anderes Hilfsmittel den relativen Anteil, also den eigentlichen Sinn und Zweck der Prozente klar.

11. ein Weihnachts-Schachtel-Set von (Schleichwerbung!?) Ikea:

Daran lassen sich doch wunderbar

1. die Ähnlichkeitsgeometrie (eine wachsende Schachtel),

2. als erstaunliche Konstante bei verschieden großen Kreisen

(vgl.    )

 erarbeiten!

Der Set hat zudem den Vorteil, dass man eine hinreichend große Schachtelzahl für eine ganze Klasse (in Partnerarbeit) hat.

12. Cavallieriverfahren bei Rotationskörpern:

B) selbsterstellte Modelle

Der Grundgedanke hinter all meinen Prototypen ist die Verbesserung geometrischer Anschaulichkeit mittels Bewegung (vgl. ): etwa bei Scherungen werden nicht nur der Anfangs‑ und der Endzustand gezeigt (oder, wie sonst im Mathe‑Unterricht üblich, an die Tafel gezeichnet), so dass sich die Schülerlnnen den Rest (eben die Bewegung) auf Gedeih und Verderb selbst dazwischen denken müssen; sondern die Scherungen werden als kontinuierliche, sichtbare Bewegungen von einem Anfangs‑ zu einem Endzustand verstanden. Bei der Scherung hat das etwa zur Folge, dass sie bei SchülerInnen als „Scheibenwischerbewegung“ (mit markanten Unterschieden dazu; s.u.) hängen bleiben kann. Mir scheint: wer das einmal gesehen hat, wird die (andernfalls sehr abstrakte) Scherung nicht so leicht wieder vergessen. Folge der Bewegungslehre ist zudem, dass SchülerInnen oftmals gar nichts mehr großartig in einem Frontalunterricht eingepaukt werden muss, sondern dass sie die Effekte selbstentdeckend, durch Rumprobieren am Modell, erarbeiten können.

Genau genommen stelle zumindest ich mir ja auch jede Scherung fiktiv als Bewegung vor.

Ein weiterer Effekt, wie er etwa am Sinus‑ und Cosinus- bzw. Tangens‑ und Cotangensmodell deutlich wird: wenn Sinus und Cosinus am selben Modell (mit markanten Unterschieden) gelehrt werden, wird ihr Zusammenhang deutlicher. Gleiches gilt für Tangens und Cotangens. Und die Verwendung zweier Modelle

• für Sinus/Cosinus einerseits und
• Tangens/Cotangens andererseits

würde wiederum verdeutlicht, dass zwischen

• Sinus/Cosinus einerseits und
• Tangens/Cotangens andererseits

doch markante Unterschiede vorliegen:

• Sinus/Cosinus sozusagen als Dampflockgestänge,
• Tangens/Cotangens sozusagen als Uhr.

Größere Anschaulichkeit ist des weiteren auch möglich, weil etwa beim Thales‑Satz‑Modell die zusätzlich zum Beweis nötige Hilfslinie schon als Konstruktionsmerkmal des Modells auftaucht.

Die vorgestellten Modelle sind nur erste Prototypen.

1. wäre in Serienfertigung sicherlich größere Genauigkeit/Funktionalität/Haltbarkeit möglich.
2. wären analoge kleine Schüler‑ und große Tafelmodelle denkbar (etwa beim Winkelmesser, damit die Schülerlnnen mit den gleichen Handwerkszeug arbeiten können wie an der Tafel).
3. fallen mir noch sehr viel mehr Modelle ein: die vorliegenden Modelle sind nur erste Versuche (analog zum Thalessatzmodell wären z.B. Mittelpunktswinkel‑ und Umfangswinkelmodelle denkbar).
4. sind durchaus auch Modelle zu anderen Gebieten als der elementaren Algebra denkbar (z.B. ein Zuordnungsmodell für Funktionsgraphen und somit tieferes Funktionsverständnis oder in der Oberstufe zwei‑ bzw. dreidimensionales Vektormodelle oder ein Sekanten‑/Tangentenmodell zur Ableitung [Sichtbarkeit des Limesprozesses!]).

ein Verlag bzw. Lehrmittelhersteller, der meine Modelle in Serie fertigt

Meine Modelle scheinen derart hilfreich, dass sie andere, bereits benutzte Modelle völlig ersetzen könnten. Nur ein Beispiel dazu: das Geodreieck, bisher Kombination von Lineal und Winkelmesser (und gerade dadurch unübersichtlich bzw. auf 180⁰ beschränkt), sollte meiner Meinung nach wieder in beide (ein Lineal nur incl. rechtem Winkel und meinen Winkelmesser) aufgespalten werden. Viele Probleme (Verwechslung, mangelnder überblick) bei der Handhabung des mit Linien vollgestopften Geodreiecks würden dadurch vermieden. Zudem würden die Schülerlnnen wieder deutlicher auf das verwiesen, was oftmals markantes Ziel des Geometrieunterrichts wäre: Konstruktion statt Ablesen. Wer beispielsweise einen Winkel langsam von 0⁰ auf aufspannt statt nur abliest, wird sich nicht mehr so leicht zwischen positiven und negativen Winkel und Winkel und Ergänzungswinkel (z.B. 90⁰ und 270⁰) vertun.

Das Problem, wenn ich hier meine bereits vorhandenen Modelle mittels Fotos vorstelle, ist nun, dass Fotos wieder gerade nicht die Bewegungen (bzw. wenn, dann nur in verschiedenen Momentanzuständen) wiedergeben können. Ich werde daher die Fotos ausführlich kommentieren müssen.

Bis auf den Schüler-Winkelmesser im „Taschenformat“ haben alle Modelle angemessene Tafelgröße, also etwa 50 x 50 cm (wenn man mal von herausragenden Stangen absieht).

Einige der Modelle (z.B. das Kathetensatzmodell) habe ich inzwischen auch in Computerprogramme (s. die Programmsammlung ) umgesetzt (zu deren Problematik s.o.).

1. Winkelmesser:

Merkmale:

1. im Gegensatz zum Gcodreieck liegt ein Vollkreis von 360⁰ vor. Somit wird jeder Winkel als Teil einer Volldrehung deutlich. Zudem sind damit auch Winkel über 360⁰ möglich (man dreht einfach über 360⁰ hinaus). Weiterer Vorteil: alle üblichen Schwierigkeiten beim Zeichnen eines Winkels über 180⁰ (z.B. 270⁰) werden ausgeschlossen.
2. mittels anderer/zusätzlicher Skalierung (vgl. Schülermodell) ist problemlos auch ein Winkel im Bogenmaß abtragbar. Konstruktionsbedingt ist allerdings (anders als im Schülermodell) keine Winkelabtragung im Uhrzeigersinn möglich (das wird durch den Mechanismus zur farbigen Darstellung des Winkels ausgeschlossen).
3. Angenommen, es soll ein Winkel an die Strecke/Gerade g im Punkt A gezeichnet werden: dazu legt man (grundsätzlich) die rote Stange auf g und den goldenen Mittelpunkt auf den Punkt A. Das ist möglich, weil die Mitte des Modells durchsichtig ist (und das Schülermodell ja sowieso). Das Abtragen des Winkels geschieht nun folgendermaßen: anfangs liegt die weiße Stange grundsätzlich noch auf der roten, und nun wird der Winkel mittels Bewegung im wahrsten Sinne des Wortes aufgespannt: 10⁰ , 20⁰ , 30⁰ ... Durch ein bestimmtes Konstruktionsmerkmal (weiße und grüne, sich gegenseitig überlappende Innenscheiben) wird der aufgespannte Winkel dabei kontinuierlich grün sichtbar (ein Effekt, der allerdings wohl nur im Tafelmodell möglich ist). Der Vorteil scheint mir dabei: der Winkel wird nicht nur als Bewegung, sondern auch als Fläche sichtbar.

Vgl. auch das Schülermodell:

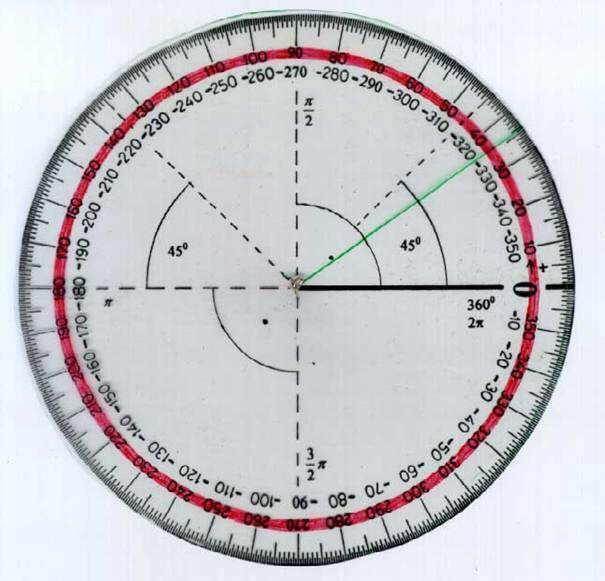
         Vgl. auch           

2. Thalessatzmodell:

Merkmale:

Gegeben ist (grün) ein Halbkreis über einer Grundstrecke AB; des weiteren ein (beweglicher!) Punkt C auf dem Halbkreis (auf dem Momentanfoto links oben). Um diesen Punkt C nun beliebig auf dem Halbkreis verschieben zu können (eben die Grundidee des Thalessatzes), ist eine Zusatzkonstruktion nötig: ein um den Mittelpunkt M der Strecke AB schwenkbarer Zeiger mit einem Nagel in C auf dem Halbkreis. Das Dreieck über AB wird nun durch ein Gummiband um A, B und C aufgespannt.

Durch diese Konstruktion sind nun kontinuierlich alle Dreiecke darstellbar bzw. verschiedenste Einzeldreiecke exemplarisch herausnehmbar. Dadurch könnte den Schülerlnnen sehr schnell und anschaulich der Gedanke kommen, daß all diese Dreiecke rechtwinklig aussehen. Womit sich die Frage ergäbe, ob das auch wirklich stimmt: eben z.B. auch für Dreiecke, deren Punkt C knapp über A oder B liegt (Herleitung der Beweisnotwendigkeit).

Damit zur Beweisidee anhand des Modells. Wegen des durch die Konstruktion notwendigen Zeigers um M liegt schon die Hilfslinie vor. Mir scheint, diese Konstruktionslinie nimmt zwar eine zentrale Idee vorweg, ohne Tip kämen die SchülerInnen aber auch kaum darauf. (Eine Verbesserung wäre es hier allerdings, das Modell überhaupt erst mit den SchülerInnen gemeinsam zu entwickeln; bzw. man bringt das fertige Modell erst ein, nachdem dieSchülerInnen die Konstruktionsidee selbst entdeckt haben.)

Mit der Hilfslinie MC liegt aber die Beweisidee (Teildreiecke AMC und BMC) nun auf der Hand.

Ein weiterer Vorteil des Modells: wegen der schnellen Beweglichkeit und der Darstellbarkeit aller denkbaren Dreiecke (bei gegebener Grundseite AB) ist die Beweisidee, anfangs an einem Beispiel durchgefiihrt, schnell auch auf andere/mehrere Dreiecke übertragbar, so daß der Eindruck vermieden wird, der ohne Modell schnell an der Tafel entsteht, wenn der ganze Beweis aufgrund des Konstruktionsaufwandes nur an einem Beispiel durchgeführt wird: daß nämlich der Beweis scheinbar nur für ein, nämlich ‑ welch ein Zufall ‑ das einzig durchgeführte Beispiel gültig ist.

Ist der Beweis erstmal erfolgt, läßt sich zusätzlich zwecks Veranschaulichung (nicht Beweis!; und deshalb erst jetzt) ein fertiger rechter Winkel in die Konstruktion legen und kontinuierlich durch sie durchziehen:

3. Scherungsmodell:

Zustand 1):

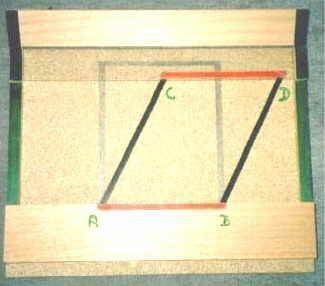
Merkmale:

Gegeben ist eine feste (rote) Strecke AB. Durch eine unter dem unteren Brett verborgene Konstruktion sind nun die Strecken AC und BD frei schwenkbar. Durch die Verbindumg CD wird dabei erreicht, daß die Strecken AC und BD immer parallel bleiben.

Im Unterricht wird nun allerdings das obere Brett erstmal zugeklappt, so daß sich folgende Bilder ergeben:

Zustände 2) und 3):

Das seien nur zwei Beispiele für die im Modell mögliche beliebige Scherbarkeit über AB bei gleichbleibender Höhe (links grün). Zusätzlich (grau schattiert) ist immer das Rechteck ABEF sichtbar (wodurch in der Tat ein Grunddanke schon vorgegeben ist; denkbar wäre es, alle Scherungen bzw. überhaupt die Scherungsidee von diesem Rechteck aus zu beginnen). Die SchülerInnen können nun jedes mögliche Parallelogramm ABDC mit diesem Rechteck vergleichen, und jedesmal wird anschaulich deutlich, daß im Vergleich mit dem Rechteck beim Parallelogramm links ein Dreieck wegfällt, das rechts hinzukommt (bzw. umgekehrt), so daß die Fläche von Parallelogramm und Rechteck gleich sein muß (Breite mal Höhe).

Wohlgemerkt: das ist mit diesem Modell kontinuierlich für alle Parallelogramme (im vorgegebenen, notwendigen Ausschnitt) möglich und nicht, wie sonst bei Tafelzeichnungen üblich, nur für ein oder zwei (so daß wieder der Eindruck aufkommen könnte, der Beweis gelte zufällig wieder nur für diese Spezialfälle).

Aber noch vor jeder Beweisidee bietet das Modell den Vorteil, die Scherung als kontinuierliche „Scheibenwischerbewegung“ zu erfahren.

Nach dem Beweis muß allerdings dasModell in den Znstand 1) geklappt werden, um dann zu zeigen, daß das „Scheibenwischermodell“ seine Grenzen hat: bei nicht‑fixer Höhe kommen keine gleichen Flächen heraus.

4. Kathetensatzmodell:

Das Modell dient dem Verfahren, den Pythagoras über die Kathetensätze zu beweisen und den Kathetensatz wiederum mittels (sehr gut zu veranschaulichender) Doppelscherung und Drehung.

Vorweg: Grundgedanke des ganzen Kathetensatz‑Beweises ist natürlich die schon notwendige Vermutung, daß a² = p • c gilt; bzw. anschaulicher, daß im Modell die Flächen des blauen Quadrats und des gelben Rechtecks gleich groß sind. Vorweg wäre also im Unterricht durchzunehmen bzw. zu wiederholen, welche Abbildungen Flächen zwar eventuell in der Form, nicht aber in der Größe verändern (halt Kongruenzabbildungen und Scherung).

Ausgangsposition 1):

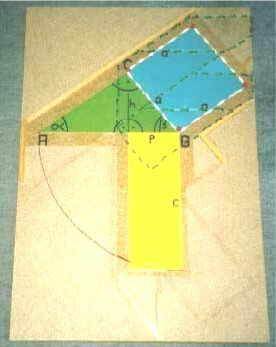
Merkmale:

Gegeben sind ein rechtwinkliges Dreieck (grün) schon mit allen im Beweisverlauf nötigen Bezeichnungen, das Quadrat (blau) über der Kathete a sowie das Rechteck (gelb) aus Hypotenusenabschnitt p und Hypotenuse c (schon incl. des „Runterklapp‑Viertelkreises“).

Vier Plexiglasstücke (grün gestrichelt) mit jeweils einem auf ihnen festen roten Nagel sind nun so angeordnet, daß die roten Nägel auf den Eckpunkten des Kathetenquadrats liegen. Um die vier Nägel ist ein (weißes) Gummiband gespannt, das das Kathetenquadrat markiert (nur ein Gummi ermöglicht Scherungen).

für den weiteren Verlauf bemerkenswert: das Plexiglasstück unten ist als einziges im Punkt B auf der Grundplatte festgenagelt, so daß später
die Drehung um diesen Punkt möglich ist. Alle anderen Plexiglasstücke  sind frei gegeneinander verschiebbar.

Durch die Konstruktion ist nun zuerst eine kontinuierliche Scherung möglich in den

Zustand 2):

Durch kontinuierliche Drehung um den vorgegebenen Fixpunkt B ergibt sich daraus wiederum

Zustand 3)

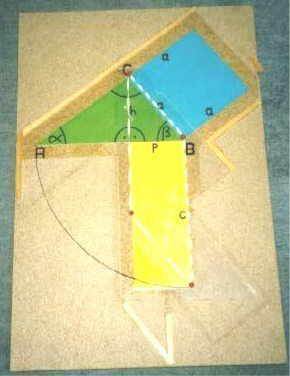
Nochmalige kontinuierliche Scherung ergibt

Zustand 4):

Es sei nochmals darauf hingewiesen, daß jede Einzel‑Veränderung kontinuierlich verläuft und sich somit insgesamt eine einzige große, kontinuierliche Bewegung ergibt. Nachteil des Modells ist, daß es vielleicht allzu suggestiv ist: z.B. scheint das Parallelogramm nach der Drehung allzu suggestiv zwischen die Schenkel a und h zu passen und die Höhe p zu haben. Jeder Einzelschritt müßte also zusätzlich durchaus theoretisch problematisiert werden.

5. Sinus‑/Cosinusmodell:

a) Sinusmodell:

Merkmale:

Gegeben sind ein Einheitskreis und rechts ein fester Zahlenstrahl zwischen ‑1 und 1 (als Verbesserung wäre nebenbei noch eine Gradeinteilung rings um den Einheitskreis denkbar). Der Einheitskreis ist beliebig um seinen Mittelpunkt drehbar, so daß sich der Punkt A beliebig auf ihm bewegen kann. Das Aufspannen des Winkels (grüner Schenkel) erfolgt nun immer von O ausgehend. Durch eine verborgene Konstruktion wird nun der „Winkelendpunkt“ A mittels der roten Linie immer parallel nach rechts auf den Zahlenstrahl projiziert, womit dort kontinuierlich der Sinus ablesbar ist.

Es wäre nebenbei (mit einigem Konstruktionsaufwand) ein Modell herstellbar, in dem passend zum Winkel automatisch der Sinus‑Graph gezeichnet würde.

Der Vorteil des Modells besteht meiner Meinung nach

1. in der Beweglichkeit/Kontinuierlichkeit, d.h. auch der Darstellbarkeit des Sinus zu jedem Winkel (nebenbei auch zu Winkeln über/unter O⁰  bzw. 360⁰);
2. wird das Grundverfahren des „Dampflockantriebs“ suggestiv deutlich;
3. wird anschaulich deutlich, daß für die Sinuswerte y nur gelten kann ‑1 < y < 1.

Durch leichte Abwandlung desselben Modells (dadurch Zusammenhang/Unterschiede Sinus/Cosinus deutlich), nämlich Drehung des ganzen Modells wie nochmals des Zahlenstrahls um O ergibt sich das

b) Cosinusmodell:

Hier muß allerdings dringend darauf hingewiesen werden, daß der Winkel nun immer vom Punkt B aus gemessen wird.

6. Tangens‑/Cotangensmodell:

a) Tangensmodell:

Merkmale:

Gegeben sind ein in einer Vorrichtung drehbarer Einheitskreis sowie rechts ein Zahlenstrahl. Von O aus ist nun wieder ein Winkel aufspannbar, wobei nebenbei in diesem Modell wieder derselbe Effekt möglich ist wie beim Winkelmesser oben: der Winkel wird grün sichtbar. Der schwarze Zeiger zeigt nun automatisch auf dem Zahlenstrahl den zum Winkel gehörigen Tangens an.

Bemerkenswert dabei ist:

1. wird durch die „Uhrähnlichkeit“ deutlich, daß der Tangens ganz anders als der Sinus funktioniert: es können Werte weit über 1 und weit unter ‑1 angenommen werden;
2. im Gegensatz zum Sinus wird nicht parallel nach „stramm rechts“, sondern entlang des schwarzen Zeigers projiziert.
3. immerhin gibt es eine Ähnlichkeit zwischen Sinus und Tangens: beidesmal liegt der Zahlenstrahl rechts (entsprechend beim Cosinus/Cotangens beidesmal oben);
4. das Modell funktioniert auch an den markanten Definitionslücken 90⁰  bzw. 270⁰: da gibt es keine Schnittpunkte zwischen schwarzem Zeiger und dem Zahlenstrahl, weil beide dann parallel zueinander liegen. Mehr noch: es wird auch ‑ durch den Zeiger in beiden Richtungen ‑ deutlich, daß kurz vor 90⁰ noch Werte weit über 1, direkt nach 90⁰ aber sofort ein Wert weit unter ‑1angenommen wird (Asymptotik‑ und Limespropädeutik).

Konstruktionsbedingt einziger Nachteil des Modells: es sind keine negativen Winkel bzw. Messungen im Uhrzeigersinn möglich (wieder durch den Mechanismus zur farbigen Winkeldarstellung ausgeschlossen).

Durch leichte Abwandlung desselben Modells (dadurch Zusammenhang/Unterschiede Tangens/Cotangens deutlich), nämlich Befestigung des Zahlenstrahls oben, ergibt sich das

b) Cotangensmodell

7. Kongruenzabbildungsmodelle:

Die drei Kongruenzabbildungen (Parallel‑)Verschiebung, Drehung und Achsenspiegelung scheinen mir geradezu Musterbeispiele dafür, daß meine Bewegungsidee hilfreich ist. Das gilt insbesondere für die 6. Klasse, wo die Konguenzabbildungen ja noch bewußt untheoretisch (oder genauer: theoriepropädeutisch) behandelt werden und es vielmehr um geometrische Anschauung und erste Konstruktionen (auch Umgang mit Zirkel, Lineal und Winkelmesser) geht. Die Frage ist da ja noch weniger „mittels welcher Abbildung (Kongruenzsätze) läßt sich zeigen, daß zwei verschiedene Figuren kongruent sind?“ als „was passiert, wenn ich auf einen Gegenstand eine Kongruenzabbildung anwende, wo wandert er (äußerlich unverändert) hin?“

Mir scheint also schlichtweg, daß man die Theorie anfangs möglichst rauslassen und statt dessen vielmehr einen Gegenstand wortwörtlich verschieben, drehen oder „spiegeln“ sollte. Das geht durchaus auch ohne explizit mathematische Modelle, also z.B. auch mit dem erstbesten Buch oder Tisch. Weil das Ziel des Mathematikunterrichts aber letztlich doch Zeichnung und Konstruktion ist (und Theorie sich dabei automatisch ergibt), scheinen mir folgende Modelle hilfreich, die nicht nur beweglich sind, sondern aufgrund der Kreidestriche auch jede dieser Bewegung automatisch an der Tafel protokollieren.

Anders gesagt: mir scheint, daß ohne meine oder ähnliche Modelle die Kongruenzlehre künstlich verkompliziert erscheinen muß: daß ein Gegenstand seine Form nicht verändert, wenn man ihn verschiebt, dreht und spiegelt, ist den SchülerInnen doch so suggestiv klar, daß man es nichtrnal problematisieren, sondern einfach tun sollte.

a) Grund‑ bzw. Verschiebungsmodell

Merkmale:

Vorgefertigt ist eine beliebige geometrische Figur (hier ein Dreieck) samt farbiger Punkt‑ und Seitenbezeichnungen. An jeder Ecke sind nun mittels (Wäsche‑)Klammern zur Eckpunktfarbe passende Kreidestücke eingespannt. Verschiebt man nun die Figur auf der Tafel, so wird automatisch die Bewegung jedes Eckpunktes aufgezeichnet. Insbesondere bei gerader Verschiebung (als Abkürzung aller anderen Verschiebungen) hat man dann automatisch für jeden Eckpunkt den Verschiebepfeil (alle Verschiebepfeile sind parallel, gleich lang und gleich gerichtet, also durch einen Repräsentanten ersetzbar). Und weil das mit einer vorgefertigten Figur passiert, bleibt suggestiv klar, daß sie ihre Form nicht verändert, sprich: kongruent bleibt.

Zur Untersuchung der gradlinigen Verschiebung könnte man das Dreieck zusätzlich auf einer Schiene hin‑ und herschieben, die mittels Saugnäpfen in beliebiger Richtung auf der Tafel befestigbar wäre.

Kommt bei allen drei hier vorgestellten Modellen hinzu, daß man wohlweislich die Ausgangsposition der Figur mit Kreide umführt und notiert, damit der Ausgangszustand festgehalten und die ganze Zeit sichtbar bleibt.

Ein möglicher Verlauf der Verschiebung:

b) Drehungsmodell:

Merkmale:

Die Figur aus a) wird nun auf einen Zeiger festgeschraubt, dessen einer Endpunkt mittels Saugnapf im vorgesehenen Drehungszentrum Z auf der Tafel befestigt wird. Die gesamte Konstruktion (Figur samt Zeiger) kann nun komplett um dieses Drehzentrum gedreht werden, wobei wieder gilt: a) es bleibt dieselbe Figur (kongruent), b) die gesamte Drehung wird aufgrund der Kreidestücke automatisch aufgezeichnet. Zeichnet man nun zusätzlich (jeweils farblich passend) die Verbindungen ZA,  ZB, ZC bzw. ZA', ZB ' und ZC ', so hat man an der Tafel nicht nur die Kreisbögen, sondern auch die (gleich großen) Drehwinkel, also alle zur Konstruktion nötigen Merkmale der Drehung.

Um als Maß für die Drehung von Anfang an den Drehwinkel messen zu können, ist zusätzlich um das Drehzentrum ein 360⁰‑Winkelmesser angebracht.

Ein möglicher Verlauf:

‑ vor der Drehung:

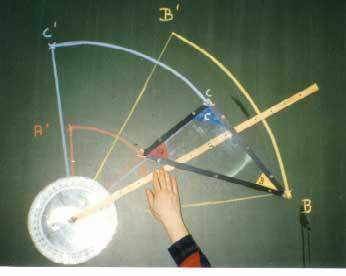
‑ nach der Drehung:

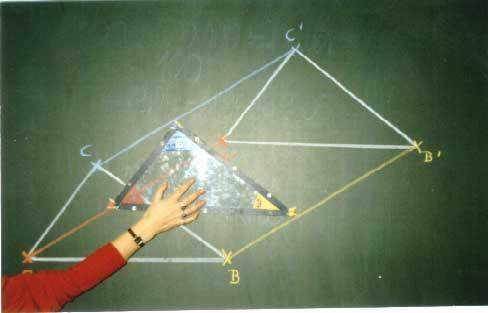
c) Achsenspiegelungsmodell:

Vorweg müßte geklärt werden, daß die Achsenspiegelung einer „Klappung“ um eine Achse entspricht (wie ich ja überhaupt meine, daß man die Modelle wenn schon nicht [wegen des Arbeitsaufwandes] mit den SchülerInnen zusammen basteln, sodoch vorweg besprechen sollte, also bevor man sie ‑ allzu suggestiv - einsetzt).

Die Klappung hat - im Gegensatz zur echten Spiegelung - nunzwar den Nachteil, daß sie dreidimensional bleibt: im Gegensatz zu a) und b) erscheinen die Bewegungsspuren nicht automatisch an der Tafel, sondern nur Anfangs‑ und Endzustand. Der Vorteil gegenüber echten Spiegelungen ist allerdings, daß das Spiegelbild ja leider immer nur virtuell bleibt und man nicht durch einen Spiegel hindurch zeichnen kann.

Das Modell besteht 1. aus einer mittels Saugnäpfen auf der Tafel zu befestigenden (Spiegel‑)Klappachse (anzulegen an einer vorgegebenen Spiegelachse auf der Tafel), 2. aus einem dazu senkrechten, mittels Scharnier an der Klappachse befestigten und um diese klappbaren Schwenkarm, an dem 3. die Figur aus a) befestigt wird. Im Ausgangszustand

werden nun die farbigen Eckkreiden auf die Tafel gedrückt. So hält man als erstes wieder den Anfangszustand. Nun wird die Figur um die Spiegelachse geklappt:

Durch erneutes Andrücken hält man den Endzustand fest. Es bleibt wieder klar: die Figur kann ihre Form nicht geändert haben, bleibt also kongruent. Und nebenbei: auf der Rückseite der Figur erscheinen nun auch die Bildpunkte A’, B’, C’, so daß man im Anschluss schnell die bei der Spiegelung umgekehrte Orientierung durchnehmen kann.

Nach Abnehmen des ganzen Modells von der Tafel liegt es nun [in Analogie zu a) und b)] nahe, alle Ur‑ und Bildpunkte miteinander zu verbinden und daraus die wichtigen Konstruktionseigenschaften (Abbildungspfeil senkrecht zur Spiegelachse, gleicher Abstand von Ur‑ und Bildpunkt zur Spiegelachse) herzuleiten.

Zuguterletzt wäre im Unterschied zur Verschiebung zu klären, daß die Abbildungspfeile zwar alle parallel, aber nicht notwendig gleich lang sind. Nicht mit diesem Modell möglich, sondern anderweitig (nur noch rein konstruktiv) zu leisten ist zudem der Nachweis, daß die Abbildungspfeile teilweise entgegengesetzte Orientierung haben können (wenn die zu spiegelnde Figur die Spiegelachse überschneidet).

d) Punktspiegelungsmodell:

Aufgrund ganz anderer (in ihrer Andersartigkeit auch zu verdeutlichender!) Abbildung ist für die Punktspiegelung auch ein ganz anderer Mechanismus erforderlich:

Merkmale:

das Modell, eine Art „Spinne“, besteht aus vier Leisten (weiß, grün, blau, rot), die um einen gemeinsamen Punkt Z jeweils in der Mitte drehbar sind. Von diesem Zentrum Z aus ist jede Leiste in beiden Richtungen mit einem Zentimetermaß versehen. Also 50 ‑ 40 ‑ 30 ‑ 20 ‑ 10 ‑ O ‑ 10 ‑ 20 ‑ 30 ‑ 40 ‑ 50.

Nun wird das Zentrum Z mittels Saugnapf auf dem Tafelpunkt befestigt, an dem gespiegelt werden soll. Die Spiegelung sei nun anhand eines Vierecks ABCD vorgemacht:

Die rote Leiste wird von Z durch A gelegt, die weiße von Z durch B, die grüne von Z durch C und die rote von Z durch D. Wenn nun A z.B. 10 cm von Z entfernt ist, so liegt A' auf der weißen Leiste bei 10 cm nur eben auf der anderen Seite von Z. Analog wird für B/B', C/C’  und D/D’ verfahren.

Dieses „Spinnenverfahren“ funktioniert für alle Vielecke (Punkte, Strecken, Dreiecke, Vierecke) in 50 cm Reichweite vom Punkt Z, also auch, wenn etwa das Vieleck den Spiegelpunkt Z umfaßt bzw. sogar, wenn A etwa auf B und B auf A abgebildet wird.

Durch eine weitere Leiste (schwarz) ist zudem für jeden Punkt zeigbar, daß dasselbe Ergebnis durch 180⁰-Drehung um Z erhältlich ist, womit die Äquivalenz von 180⁰‑Drehung und Punktspiegelung für jeden Punkt klargemacht werden kann.

Zuguterletzt ist das „Spinnenverfahren“ später
unverändert auch für Ähnlichkeitsabbildungen zwecks zentrischer Streckung verwendbar. Auch da wird der Strahlencharakter von einem Zentrum aus ja wieder wichtig.

8. Proportionalitätsfächer