Matrizen(multiplikation)
Angenommen, bei einem familiären Mittagessen gibt's Fischstäbchen mit Kartoffeln:
|
→
 |
→
 |
|
→
 |
(Man beachte, dass die Essgewohnheiten der Kinder, also
, nicht von denen der Erwachsenen, also
, abhängig sind.)
Die Familie besteht aus
|
→
 |
|
Bleiben wir aber zuerst bei den einzelnen Essensbestandteilen, also
- erst den Fischstäbchen,
- danach den Kartoffeln,
bevor wir beide Essensbestandteile zusammen betrachten.
Zu a., also den Fischstäbchen:
Erinnern wir uns vorweg, dass es zwei (genauer: drei) Arten der Vektormultiplikation gibt:
A. die s-Multiplikation, d.h.
- die Multiplikation
- eines Skalars (einer Zahl)
- mit einem Vektor;
- das Ergebnis ist ein verlängerter/verkürzter und eventuell "umgedrehter"" Vektorr:
Skalar mal Vektor = (neuer) Vektor
B. das Skalar-Produkt, d.h.
-
die Multiplikation
- eines Vektors
- mit einem (anderen) Vektor;
- das Ergebnis ist ein Skalar:
Dieses Skalarprodukt funktioniert beispielsweise so:
•
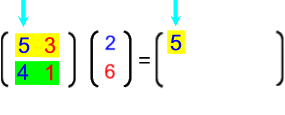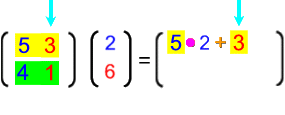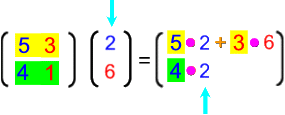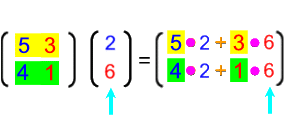
= 5 • 2 + 3 • 6 = 10 + 18 = 28
Und wenn wir den ersten Vektor ausnahmsweise mal quer legen, ansonsten aber nichts ändern, ergibt sich
•
= 5 • 2 + 3 • 6 = 10 + 18 = 28
Insgesamt werden in der Familie also 28 Fischstäbchen verzehrt.
Halten wir aber schon mal fest:
- in
•
muss der Vektor
natürlich genauso "hoch" sein wie der Vektor
,
- in
•
muss der quergelegte Vektor
genauso "breit" sein, wie der Vektor
"hoch" ist.
Zu b., also den Kartoffeln: hier ergibt sich
(wieder mit dem Skalarprodukt)
analog zu a.
•
= 4 • 2 + 1 • 6 = 8 + 6 = 14
bzw.
•
= 4 • 2 + 1 • 6 = 8 + 6 = 14
Insgesamt werden in der Familie also 14 Kartoffeln verzehrt.
Und wieder ist festzuhalten:
|
|
Nun wollen wir gleichzeitig ermitteln, wieviele Fischstäbchen und wieviele Kartoffeln in der Familie insgesamt verzehrt werden.
Mit den obigen Einzelergebnissen für Fischstäbchen und Kartoffeln liegt es nahe, folgendermaßen vorzugehen:
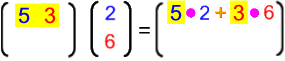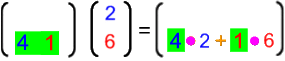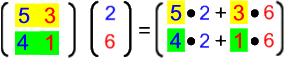
Offensichtlich funktioniert das insgesamt so:
Oder vielleicht noch anschaulicher:
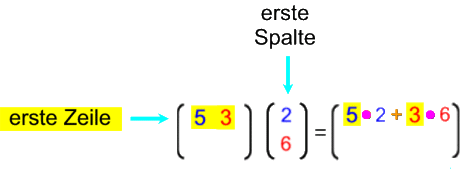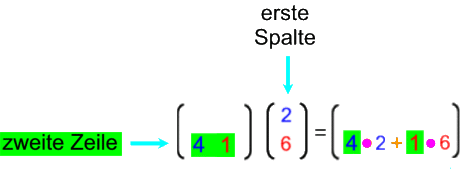
Da in den Rechnungen rechts massenhaft Multiplikationen stehen
(allerdings auch einige Additionen),
nennen wir auch das, was links geschieht, "Matrizenmultiplikation" und ergänzen dort deshalb ein Malzeichen:
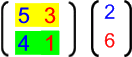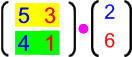
Genau genommen haben wir aber bislang nur
- eine 2 x 2 - Matrix, nämlich
, - mit einem Vektor, nämlich
,
multipliziert. Aber man kann den Vektor ja schon als eine 1 x 2 - Matrix ansehen. Vektoren sind - so gesehen - also nur besonders "schmale" Spezialfälle der Matrizen
(woraus folgt, dass die Rechenregeln für Matrizen auch für Vektoren gelten sollten, und wir hatten ja tatsächlich die Matrizenmultiplikation aus dem Skalarprodukt für Vektoren hergeleitet).
Um jetzt aber mal zwei "richtige" Matrizen miteinander zu multiplizieren, erfinden wir einfach eine zweite Familie,
- in der ebenfalls Fischstäbchen und Kartoffeln gegessen werden.
- Wir setzen dabei des weiteren voraus, dass alle Erwachsenen bzw. Kinder genauso viele Fischstäbchen und Kartoffeln essen wie in der ersten Familie,
- und ändern nur die Familiengröße: die
zweite Familie soll aus 3 Erwachsenen (Eltern + Oma) und 5 Kindern bestehen, womit sich als neuer "Familien-Vektor"
ergibt.
Damit könnten wir analog zu oben
•
rechnen, aber wir wollen im folgenden beide Familien "in einem Abwasch" erledigen, rechnen also
•
Mit der oben hergeleiteten Multiplikationsregel ergibt sich
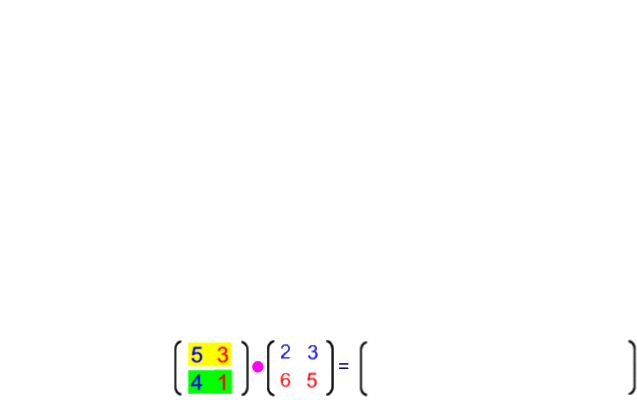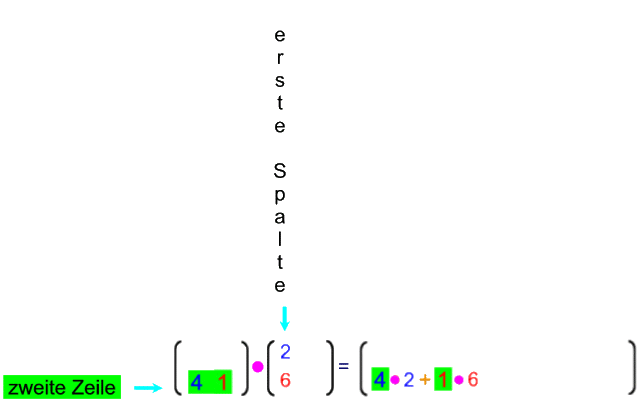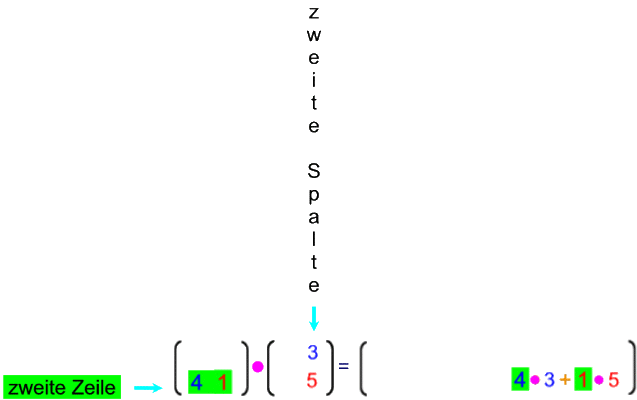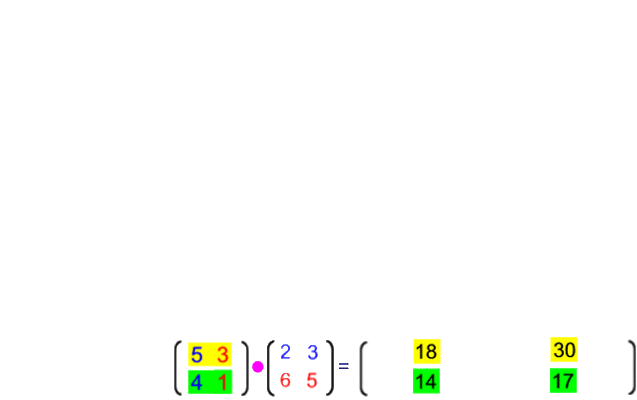
Schauen wir uns nun die Zusammenhänge genauer an:
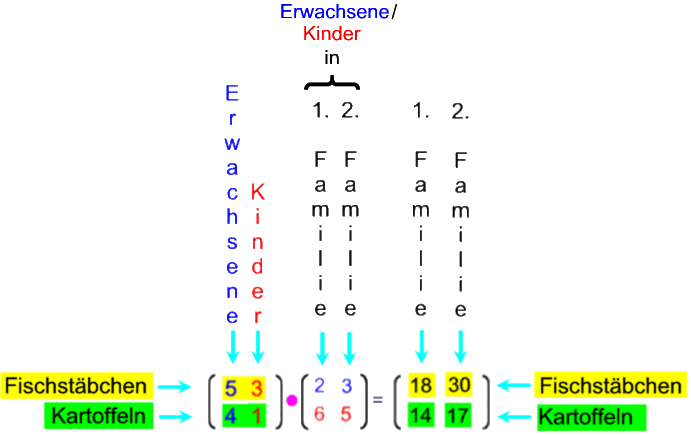
Und da ich mir ja zu keiner Veranschaulichung zu schade bin:
oder
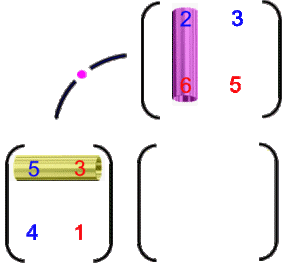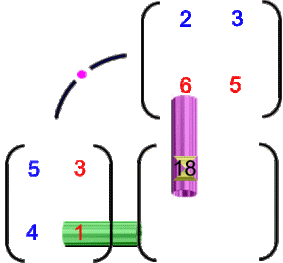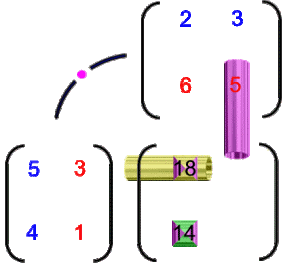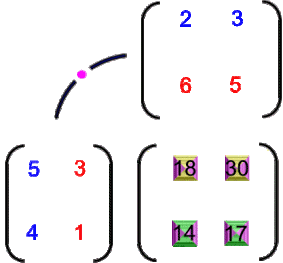
Bei all dem ist
die "Verteilungs-Matrix": sie zeigt an, wie viele
Fischstäbchen bzw. Kartoffeln die Erwachsenen bzw. Kinder essen,
die "Familien-Matrix": sie zeigt an, wie viele
Erwachsene und Kinder es in jeder der beiden Familien gibt;
die "Familien-Verteilungs-Matrix": sie zeigt an, wie viele
Fischstäbchen und Kartoffeln in jeder der beiden Familien gegessen werden.Insgesamt haben wir also
- aus der Verteilungs-
- und der Familien-
- die Familien-Verteilungs-Matrix
gemacht.
Nehmen wir nun mal an, beide Familien wollten
zusammen essen. Dann müssten wir nur noch die Vektoraddition
+
=
durchführen, wobei
die Einkaufsliste wäre.
Wir müssten also für beide Familien zusammen 48 Fischstäbchen und 31 Kartoffeln kaufen
(völlig verschwunden sind da hingegen die Informationen,
- wie viele Fischstäbchen bzw. Kartoffeln Erwachsene bzw. Kinder essen,
- wie viele Familien am Essen teilnehmen
[immerhin das noch war in
sichtbar],
- wie viele Erwachsene und wie viele Kinder es in jeder der beiden Familien gibt.
Aber bei der Einkaufsliste
wären ja all diese Details auch uninteressant.).
Nachdem wir derart anhand des Anwendungsbeispiels "Familienessen"
- eine halbwegs anschauliche Vorstellung von Matrizen bekommen und
- die Matrizenmultiplikation hergeleitet haben,
schauen wir uns nun wieder die rein (inner-)mathematischen Eigenschaften von Matrizen und ihren Multiplikationen an:
- Wie schon bei einer einzigen Familie, also bei
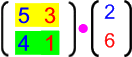, deutlich wurde, kann eine Matrix (hier die rechte) auch nicht-quadratisch (hier ein Vektor) sein.
Noch deutlicher wird das, wenn wir uns vorstellen:
- es gibt nicht zwei, sondern drei Essenszutaten, z.B. zusätzlich noch Salatblätter. Dann sieht die linke Matrix z.B. so aus:
Wenn wir noch bei einer einzigen Familie bleiben, ergibt sich damit
.
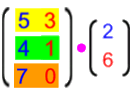Die Ergebnismatrix gibt an, wie viel von allen (jetzt drei) Zutaten die erste Familie braucht, d.h. diese Ergebnismatrix hat jetzt automatisch die Höhe 3:
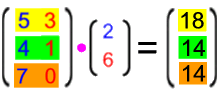
Die Ergebnismatrix hat also immer
- die Höhe der ersten und
- die Breite der zweiten Matrix:
- Nehmen wir nun des weiteren an, dass nicht eine oder zwei, sondern gleich vier Familien essen, so ergibt sich
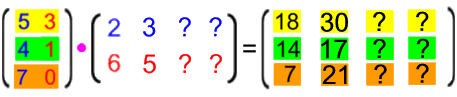
bzw.
(Spätestens hier wird man anhand der Fragezeichen bemerken, dass mich konkrete Zahlen wenig interessieren und ich zum schnöden Rechnen eh zu faul bin. Viel lieber verschwende ich meine Zeit auf die Veranschaulichung des Prinzips.)
- einige rechnerische Eigenschaften:
- wir hatten es ja so gewollt: die Multiplikation zweier Matrizen ergibt wieder eine
(Wie oben gesagt, müssten die Vektoren als Teilmenge der Matrizen ebenfalls eine multiplikative "Gruppe" bilden. Aber bei der s-Multiplikation ergibt die Rechnung "Vektor • Vektor" doch
keinen Vektor, sondern nur einen Skalar, also eine Zahl!?
Aber Skalare bzw. Zahlen sind auch nur [eindimensionale] Spezialfälle von Vektoren bzw. Matrizen: ein Skalar bzw. eine Zahl ist ein 1x1-Vektor bzw. eine 1x1-Matrix.
Also gilt doch "Vektor • Vektor = Vektor".)
- Die Matrizenmultiplikation besitzt tatsächlich ein "neutrales Element", durch das nichts verändert wird, und zwar jene quadratische "Einheits-" oder "Identitätsmatrix",
- deren Hauptdiagonale von links oben nach rechts unten nur aus Einsen besteht, während
- alle anderen Elemente Null sind:
Das sei hier nur knapp behauptet - und man probiere es einfach mal aus.
- Aber nicht zu allen, sondern nur zu einigen quadratischen Matrizen M1 gibt es eine "inverse" Matrix M2 , so das M1
• M2 die Einheitsmatrix
ergibt
(was wieder nur behauptet sei; den Nachweis spare ich mir, da es solch eine inverse Matrix ja nicht immer gibt).
- Die Matrizenmultiplikation ist in der Regel nicht kommutativ. Z.B. ist
-
-
- und deshalb
.
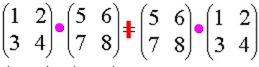Die Matrizenmultiplikation kann aber schon allein aus einem ganz einfachen Grund nicht kommutativ sein. Erinnern wir uns dazu an das Beispiel
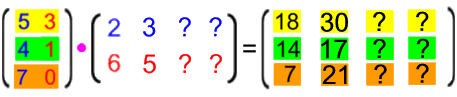
oben für vier Familien bei drei Essenszutaten. Die umgekehrte Multiplikation
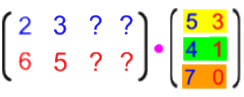
ergibt keineswegs (nur) ein anderes Ergebnis, sondern sie ist (sogar) schlichtweg unmöglich, weil die zweite Matrix nicht so hoch wie die erste breit ist.
Wenn auch die Vektoraddition ein Spezialfall der Matrizenaddition sein soll, liegt folgende Definition der Matrizenaddition nahe:
Oder:
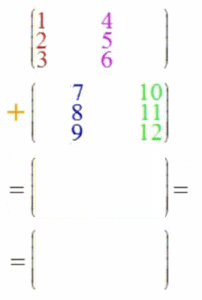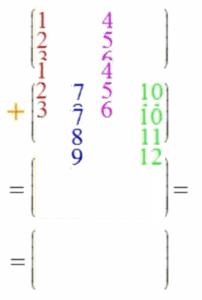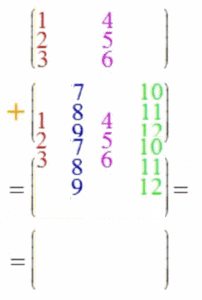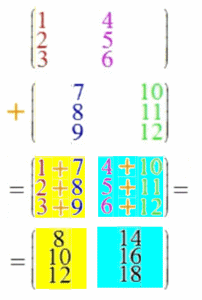
Oder:
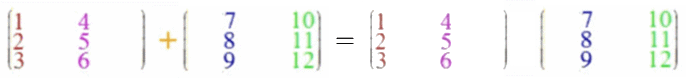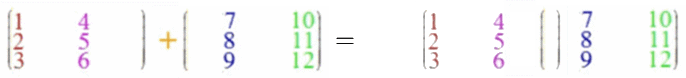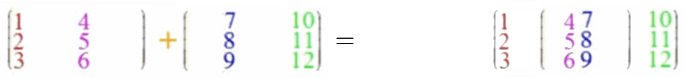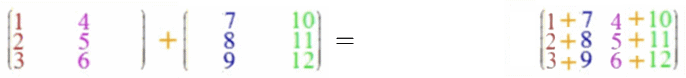
Und diese Matrizenaddition ist - im Gegensatz zur Matrizenmultiplikation - kommutativ
(weil die
Matritzenaddition sich nämlich direkt aus der Zahl-/Skalaraddition ergibt und die Additionen einfacher Zahlen/Skalare in der Matrix
kommutativ sind)!
Bei der Matrizenaddition müssen die beiden Matrizen exakt dieselbe Form
(dieselbe Höhe [hier beidemal 3] und dieselbe Breite [hier beidemal 2])
haben, aber die Höhe der zweiten (hier 3) muss nicht
(wie bei der Matrizenmultiplikation)
gleich der Breite der ersten (hier 2) sein.