: das sagt sich so leicht

Fragt sich nur, was die SchülerInnen da eigentlich können sollen:

1. einmal an einem einfachen Beispiel herleiten?
2. für jedes x-beliebige, auch kompliziertere Beispiel (wieder) herleiten können?
3. die Feinheiten von 

verstehen?

4. die Formel auf einfachere und komplexere (Anwendungs-)Beispiele anwenden können, und zwar

• ohne tieferes Verständnis, indem einfach der Taschenrechner ("nCr") benutzt wird,
• ggf. auch ohne Taschenrechner?

Alles zusammen wäre ein ganz erhebliches Programm - und das allemal, wenn die SchülerInnen all das nicht nur "von 12 Uhr bis Mittag"

(wie üblich nur bis zur nächsten Klassenarbeit),

sondern auch langfristig können sollten.

Im Folgenden möchte ich mir 1. und 2., also die Herleitung, nur kurz anschauen, und 4., also die Anwendung, nur an einem "entlarvenden" Beispiel. Mein Hauptprogrammpunkt ist also 3., d.h.

Vorweg aber doch kurz zu 1., also der Herleitung der Formeln, und zwar anhand eines Schulbuchklassikers, in dem das so aussieht:

(Der Fairness halber sei ergänzt, dass da auch noch eine erklärende [?] Grafik mit abgedruckt ist.)

Nach diesem Beispiel folgen in dem Schulbuch sofort die allgemeinen Formeln, also

D.h. aber, dass nach einem einzigen, noch relativ einfachen Beispiel sofort eine in Schüleraugen doch wohl abschreckender Wust "ganz schön schwieriger" Formel folgt:

• ,
• ,
• .

Davon ist bereits die erste, also , durch den vorstehenden Text schlecht motiviert, denn dort stand statt .

Günstiger wäre also wohl und daraus dann folgend.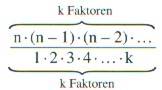

Und nochmals günstiger fände ich es auch, wenn man in die Faktoren des Zählers und des Nenners jeweils übereinander schreiben würde, damit auch durch solche klare Anordnung deutlich wird, dass im Zähler und Nenner gleich viele Faktoren vorliegen.

Unschön daran ist aber nach wie vor, dass der Zähler mit "..." endet, was doch immerhin zu dem Irrtum verleiten könnte, es gehe dort folgendermaßen weiter:

n • (n-1)•(n-2)• ... •3•2•1 = n!

Ohne "..." am Ende des Zählers würde die Formel so aussehen:

Aber mit dem dann auftauchenden Faktor (n-[k-1]) wäre das für (Mittelstufen-)SchülerInnen wohl doch zu kompliziert

(dass [k-1] auftauchen muss, damit im Zähler k Faktoren stehen).

Überhaupt findet hier etwas in Schüleraugen und -ohren wohl höchst Umständliches und kaum Motiviertes statt: aus der relativ einfachen Anfangsformel werden die zwei äußerst umständlichen (aber allgemeingültige!) Formeln und , und wir werden einige Umwege brauchen, um an letzteren wieder das (Schlangen-)Prinzip zu verdeutlichen, das man schon bei der Herleitung von hätte entdecken können.

Kleiner Einschub:

da bin ich doch "richtiger" Mathematiker: mich interessieren die Formeln und die Zusammenhänge zwischen ihnen - aber doch nicht die schnöden Ergebnisse

(deren Berechnung überlasse ich mit größter Verachtung dem Rechenknecht Taschenrechner).

Und das eben auch, weil die Formeln meistens hübsch (relativ) einfach

(wenn auch abstrakt),

die Ergebnisse oft aber grausig unübersichtlich sind

(und an ihnen nicht mehr ihre Herkunft ablesbar ist).

Z.B. beim Lotto "6 aus 49":

= 13.983.816

Es kommt halt drauf an, was man sucht: wenn ich die Gewinnwahrscheinlichkeit beim Lotto ermitteln will, ist natürlich nichtssagend, hingegen sehr aussagekräftig.

Nun kann man sich natürlich streiten, was eigentlich im Matheunterricht vordringlich "gesucht" wird:

1. die Lösung eines konkreten Anwendungs-, also z.B. des Lottoproblems? Ich wage doch mal zu bezweifeln, dass das überhaupt eine echte Anwendung ist, denn wer lässt sich schon durch das Ergebnis vom Lotto abhalten oder zu ihm ermutigen.

(Der penetrant moralische Zeigefinger "spielt nicht Lotto!" hinter ist nicht nur unangebracht, sondern trifft auch verlässlich ins Leere.)

2. anhand von "Anwendungsaufgaben" ein "Gefühl" für statistische Prozesse in der Wirklichkeit - und auch rechnerisches Handwerkszeug zur Bearbeitung solcher Prozesse? In ersterem Fall braucht man nur die Ergebnisse, in letzterem die Ergebnisse und die Formeln.
3. die Kenntnis von, ja das Jonglieren mit "innermathematischer Strukturen"? Dann braucht man nur die Formeln

(das Lottospiel ist dann nur eine "Vorstellungskrücke" bei der Erarbeitung innermathematischer Strukturen).

Die Formel ist nun aber in doppeltem Sinne kaum brauchbar:

1. ist sie sehr lang und damit kaum merkbar,
2. kann man mit den Pünktchen am Ende des Zählers kaum rechnen.

Die Autoren des Buches ziehen daraus die üblichen Konsequenzen:

  zu 1.: sie führen die übliche Kurzschreibweise ein,

  zu 2.: sie führen die Schreibweise ein.

Das aber ist mehrfach problematisch:

• kann gar nicht hergeleitet werden, sondern ist nur ein einfacherer Name bzw. eine einfachere Schreibweise

(vgl. "Dafür schreibt man auch kurz ");

• wäre zwar aus herleitbar, aber das sparen sich die Autoren völlig

(und zudem verschieben sie in eine kleiner gedruckte Randanmerkung, was so aussieht, als wäre sie ihnen unwichtig; das aber heißt doch, dass die SchülerInnen nur benutzen sollen, was wiederum bedeutet, dass sie nur "sinn- und verstandlos" in den Taschenrechner eingeben können);

• hinter den beiden neuen Formeln und

(und nur mit denen rechnet man ja später)

verschwindet völlig die Herleitung: man sieht ihnen nicht mehr an, wie sie sich aus dem "Problem" ergeben;

• insbesondere verschwindet hinter der äußerst kurzen Schreibweise schnell, dass sie eine zwar praktische, aber doch auch rasante Abkürzung von ist; und alle Abkürzungen (wie z.B. auch Potenzen) sorgen doch schnell dafür, dass der entsprechende Sachverhalt für SchülerInnen völlig abstrakt bleibt und sich daher gerne viele Fehler einschleichen

(ich fänd's z.B. durchaus bezeichnend, dass ein Schüler prompt mit kⁿ verwechselte, denn bei der Potenz steht der Exponent n schließlich auch schräg "über" der Basis k).

Wie also ergibt sich aus ? Bzw. es sei "nur" an einem Beispiel gezeigt, weshalb beide Formeln identisch sind, wobei ich aus gutem, wenn auch noch zu erklärendem Grund bewusst nicht das ungünstige Beispiel aus dem Buch, sondern nehme.

Dann wird

                          zu =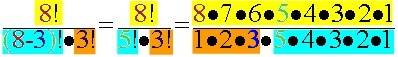

                                                                                = =

                                                                                = ,

und das ist nichts anderes als die konkretisierte Form von eben für n = 8 und k = 3.

Der Faktor (8 - 3)! im Nenner von ist also einzig und allein dazu da, vom vollständigen Zähler den Ratten- bzw. Schlangenschwanz wegzuschnibbeln, so dass dort im Zähler nur noch übrigbleibt, also genauso viele Faktoren wie im Nenner, nämlich k = 3.

überhaupt erst in der Form wird aber das Prinzip überdeutlich.

Und mit "Schlange" haben wir endlich auch eine Metapher, die = veranschaulicht

(und zwar auch dann, wenn das ursprüngliche Auswahl-Problem verschollen bleibt)

• im Zähler steht nämlich mit sozusagen der Anfang der Schlange ,
• im Nenner steht hingegen mit sozusagen das Ende der Schlange ,
• und Anfang sowie Ende sind gleich lang, bestehen nämlich aus k = 3 Faktoren:

In = gibt also

•        n = 8 die                 änge der (Gesamt-)Schlange
• und k = 3 die (gleiche!) Länge des bzw. des Endes

an.

Noch eindrücklicher ist die Metapher allerdings, wenn man

folgendermaßen darstellt:

(vgl. zur Schlangenmetaphorik auch
 
)

Wichtig daran ist auch, dass einige Zahlen (hier 4 und 5) unbenutzt bleiben können, also die Mitte der Schlange übrig bleibt.

Genauso ist es aber auch möglich, dass

1. von der Schlange rein gar nichts übrig bleibt,
2. Teile der Schlange

(und hier versagt bereits die Schlangenmetapher)

mehrfach "benutzt" werden. Das geschieht beispielsweise beim Anfangsbeispiel aus dem Buch, also , wo die 3

• sowohl Teil des                                    (des Zählers)
• als auch Teil des                                                                    Endes        (des Nenners) ist:

=

Wenn es um die Erkenntnis des "Schlangenprinzips" geht, ist das Einstiegsbeispiel aus dem Schulbuch also denkbar ungünstig.

(Aber vermutlich wollten die Autoren auch gar nicht auf dieses "Schlangenprinzip" hinaus, denn sonst hätten sie ja statt auch besser geschrieben.)

Ungünstig bis geradezu irreleitend ist aber auch noch aus einem anderen Grund: legt

• nicht nur richtig nahe, dass oben und unten je 3 Faktoren auftauchen müssen,
• sondern auch fälschlich, dass die Zahl k (hier 3) immer sowohl im Zähler als auch im Nenner auftauchen muss.

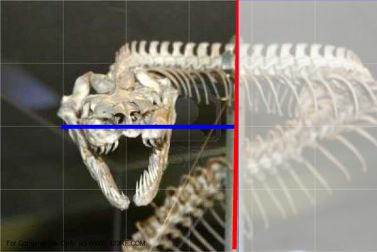
Manchmal ist Brutalität hilfreich, um sich ein mathematisches Bild zu merken: man nehme eine Schlange, hacke ihren Kopf und Schwanz ab

(und meines Wissens können Schlangen nicht, wie angeblich Regenwürmer, danach wieder einen vollständigen Körper ausbilden werden),

werfe das Mittelteil weg und dividiere den Kopf durch den Schwanz. 

Oder eine andere Veranschaulichung:

Ein nettes Schmankerl ergibt sich, wenn man SchülerInnen bittet, statt doch mal zu berechnen:

• Eine erste große Gruppe gibt stumpf in den Taschenrechner ein und erhält dann "Error". Aber was bedeutet das?

(wenn SchülerInnen überhaupt so weit fragen):

• ist es wirklich falsch (unmöglich)
• oder ist der Rechner nur wieder mal - wie etwa bei sehr großen Fakultäten - an seine Grenzen gestoßen?

• Eine zweite große Gruppe rechnet mit der Formel und erhält dann . Ein Teil dieser Gruppe fragt dann, was denn eigentlich (-5)! ist, während ein anderer Teil immerhin dann erkennt, dass das gar nicht definiert, also wohl Blödsinn ist.
• Eine dritte Gruppe wendet das Schlangenprinzip an:
  • aus einer 3-gliedrigen Schlange
  • brauchen wir den 8-gliedrigen Anfang (für den Zähler) sowie das 8-gliedrige Ende (für den Nenner).

  Und dann erst merkt diese Gruppe, dass das wohl kaum möglich ist.

• Die allermeisten haben also vor lauter Formeln längst das eigentliche Problem vergessen, bzw. ganz wenige rechnen erst gar nicht los, sondern sagen sofort, dass Blödsinn ist, weil man nicht (ohne zurücklegen) 8 aus 3 Dingen ziehen kann.

Immerhin bemerkenswert daran finde ich aber, dass hier mal eine "offene" Aufgabe in dem Sinne vorliegt, dass man auf vier verschiedene Arten merken kann, dass da "etwas nicht stimmt".

Es fragt sich doch sehr, ob die SchülerInnen die Formeln überhaupt verstehen oder sie nur anwenden können müssen/sollen.

Aber was heißt schon "nur"?: diese "Anwendung" ist ja oftmals das eigentliche Problem. Dazu ebenfalls ein Beispiel aus dem bereits oben zitierten Buch:

Von dieser Aufgabe sei nur Aufgabenteil a) genauer betrachtet - und der ist schon schwierig genug.

Oder genauer:

• Wenn man's den SchülerInneN an mehreren ähnlichen Beispielen vorgemacht und eingeblüut hat, werden sie wohl auch diese Aufgabe lösen können!?
• Aber hätte einE mittelprächtigeR SchülerIn in der 9. Klasse überhaupt die mindeste Chance,  selbst auf eine Lösungsidee für a) zu kommen?

Ich will hier gar nicht die Gedanken verraten, die zur "Lösungsformel" 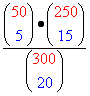führen. Aber ist doch schon ein ganz erhebliches Monstrum, und zwar um so mehr, wenn jede Klammer eine rasante Abkürzung für wüste Rechnungen ist.

Dass ich nicht den Weg verraten habe, wie man zu kommt, hatte durchaus Hintersinn. Hier liegt ein schönes Beispiel dafür vor, dass man mal

(was im Unterricht viel zu selten gemacht wird)

von der Lösung, also , ausgehen und damit "rückwärts" die Mathematisierung verstehen könnte. Hilfreich wären da

1. eine Strukturanalyse:

• im Zähler finden zwei (wegen des Multiplikationszeichens parallele) Ziehungen statt

(und das ist genau der Stolperstein: dass

• nicht nur - wie die Aufgabenstellung a) fast suggeriert - aus den Gewinnlosen,
• sondern auch aus den Nieten gezogen wird),

• im Nenner eine.

2.  ein doppelter Zahlenvergleich:

• Wo tauchen die Zahlen aus der Aufgabenstellung in auf?
• Wie hängen die Zahlen in zusammen?:

• 50 + 250 = 300 ,
•   5 +   15 =   20 .

Das wird noch verständlicher, wenn man die 's probeweise mal als genauso notierte Vektoren ansieht, denn bei ihnen ergibt sich .

überhaupt hat für mich etwas ästhetisches:

Ein halbes Jahr später frage ich die SchülerInnen, was sie noch von bzw. konkret z.B. von wissen. Und prompt kommt die Antwort "Anfang der Schlange durch Ende der Schlange".

Leider wissen sie aber nicht mehr, dass es um "Ziehen ohne zurücklegen" geht - haben sie sich also das Falsche gemerkt?

Ein schöner -Rechner vor allem für sehr große Werte: