Nullstellen oder Schnittpunkte mit der y-Achse?

Rechnen (als grundlegendes Handwerkszeug) ist ja auch wichtig, aber oftmals

• fehlt es SchülerInneN doch an der Kenntnis (und Einhaltung!) grundlegender Rechenregeln,

• rechnen sie einfach (?) drauflos ("Schrottschussladungen"), statt sich erstmal die genauen Strukturen (aus denen die anzuwendenden Rechenregeln folgen) anzuschauen,

• rechnen sie völlig kopflos, also ohne jede Anschauung.

Rein algebraische Funktionen, also kleine Rechenmaschinen, die jeden beliebigen Input nach einer stumpfen Regel abarbeiten, haben ja durchaus auch ihren schlichten Reiz (vgl. auch ).

Der Kick

(der einen Riesenfortschritt nicht nur für die Mathematik, sondern auch für die Neuzeit brachte)

kam aber doch erst mit   in die "Funktionenlehre". Dieser Kick bestand in der neuen Möglichkeit, sich die arg abstrakten Funktionen (z.B. y = x² )  zu veranschaulichen, weil man anhand der Funktionsgraphen (im Koordinatensystem) einen überblick über den kontinuierlichen Verlauf gewinnen konnte:

z.B.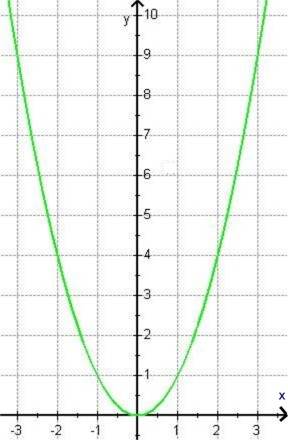

Hingegen waren bei der rein algebraischen Funktionsvorschrift immer nur Momentaufnahmen (die Zuordnung des y zu jeweils einem [und insgesamt nur sehr wenigen] x ) möglich:

x y = x2 -3 9 -2 4 -1 1 0 0 0,5 0,25 1 1 3 2 4 3 9

Aus solchen (wenigen) Momentaufnahmen konnte man sich aber wahrhaft kein Bild über den Gesamtverlauf der Funktion machen.

Funktionsgraphen dienen vor allem dazu, einen groben überblick über den Funktionsverlauf bzw. die Funktionsentwicklung zu bekommen.

Entscheidend für das grundsätzliche Aussehen "ganzrationaler" Funktionen

(genauer: der Graphen solcher Funktionen)

ist dabei der höchste Exponent

(für sehr große negative oder negative x sind die Summanden mit kleinerem Exponenten unerheblich, da dort vor allem der Summand mit dem größten Exponenten "explodiert"):

• Funktionen geraden Grades (also z.B. y = x ² oder y = 3x ⁴-5x³+7x²-6x+8) sind "im Prinzip parabelförmig", sehen also etwa folgendermaßen aus:

Es ergeben sich höchstens in der "Mitte" kleine Schlenker, während die Graphen "außen" parabelförmig bleiben:

• Und alle ("ganzrationalen") Funktionen ungeraden Grades (also z.B. y = x³ oder y = 0,5x⁵-3x⁴-5x³+7x²-6x+8) sehen "s-förmig" aus:

Auch hier kann es in der "Mitte" kleine Schlenker geben, während die Graphen "außen" s-förmig bleiben:

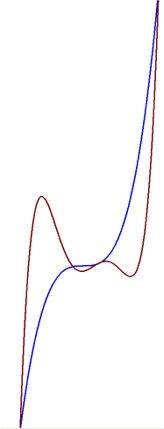
In Termen wie3x⁴-5x³+7x²-6x+8 oder 0,5x⁵-3x⁴-5x³+7x²-6x+8 ist nicht nur der höchste Exponent entscheidend, sondern überhaupt der ganze Summand, in dem dieser höchste Exponent auftaucht:

1. entscheidet sich an der Zahl (auch "Leitkoeffizient" genannt) vor der höchsten x-Potenz , ob die Kurve gestreckt (z.B. für 3 >1 ) oder gestaucht (z.B. für 0,5 < 1) ist,

2. entscheidet sich da (am Vorzeichen der Zahl) auch, ob die Kurve im Prinzip

• so oder so

• bzw. so oder so aussieht.

Anders gesagt: der ganze restliche Schlamassel (Summanden mit kleineren Exponenten) ist völlig unerheblich für den prinzipiellen Funktionsverlauf und

1. trägt höchstens einige "Schlenker in der Mitte" (s.o.) zu ihm bei,

2. verschiebt den Graphen ein wenig horizontal und/oder vertikal.

Bis hier kennen wir also (allein aufgrund des Summanden mit dem höchsten Exponenten) schon den prinzipiellen Funktionsverlauf und wissen wegen a. nur noch nicht so genau, wo der Funktionsgraph denn nun eigentlich liegt

(weshalb auch bislang das Koordinatensystem absichtlich weggelassen wurde).

Wenn man nun aber doch halbwegs wissen will, wo der Funktionsgraph liegt, braucht man einige (am besten leicht zu errechnende und merkbare) "Fixpunkte". Zusammen mit den Kenntnissen über die grundsätzliche Form des Graphen kann man dann leicht eine Planskizze zeichnen, z.B.

• bei der Geraden y = 2x + 3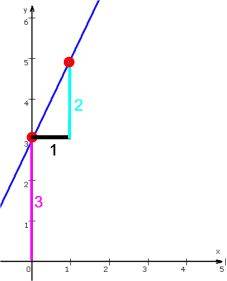

• oder bei der Parabel y = x²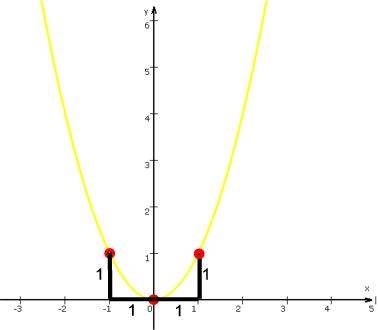

Schon allein anhand dieser spezifischen Fixpunkte bei der Geraden und der Parabel wird klar:

1. erleichtern sie enorm die Konstruktion,

2. aber es sind doch unterschiedlich gewonnene Punkte, es gibt also keine Einheitlichkeit, was zur Folge hat, dass man für jede Funktionensorte spezifische Fixpunkte auswendig lernen müsste.

Kommt hinzu, dass - wie wir gesehen haben - Funktionsgraphen (u.a. horizontal) verschoben sein können und dann spezifische Eigenarten nicht unbedingt nah am Ursprung bzw. der y-Achse liegen.

(Weil man es von einfachsten Funktionen, bei denen es ja auch sinnvoll ist, so gewöhnt ist, ist man ja immer versucht, Wertetabellen rund um den Ursprung bzw. den x-Wert 0 anzulegen. Aber manchmal ist da bei einer Funktion reichlich wenig "los", sondern findet Entscheidendes ganz woanders statt; vgl. etwa 

   )

Wir brauchen also "Fixpunkte", die nicht nur markant und einfach zu errechnen sind, sondern auch

• für möglichst viele Funktionensorten aussagekräftig sind,

• an Stellen liegen, wo für den Funktionsverlauf wirklich Entscheidendes "los" ist.

Und hier eben kommen - endlich! - die Nullstellen und der Schnittpunkt mit der y-Achse ins Spiel.

Die Gemeinsamkeit von "Nullstellen" und "Schnittpunkten mit der y-Achse" besteht darin, dass der Graph in beiden Fällen eine der beiden Achsen schneidet, nämlich

• bei "Nullstellen" die x-Achse,

• in "Schnittpunkten mit der y-Achse" natürlich die y-Achse.

Und schon fangen die sprachlichen Probleme an:

1. Irritation: es muss ja kein Schnitt zustande kommen, sondern der Funktionsgraph kann eine Achse auch  nur berühren.

(Vgl. etwa   )

Aber es gibt halt kein Wort, das sowohl "schneiden" als auch "berühren" bedeutet

(mathematisch hingegen ist alles mit x = 0 oder y = 0 eindeutig).

2. Irritation:

• es ist häufig von "Nullstellen", aber nur höchst selten von "Schnittpunkten mit der x-Achse" die Rede ist, während umgekehrt

• es bei den "Schnittpunkten mit der y-Achse" überhaupt kein Wort-äquivalent zu "Nullstellen" gibt.

Genau genommen ist nämlich

• mit "Nullstelle" nur der x-Wert (die Einzelkoordinate) gemeint, an der die x-Achse berührt bzw. geschnitten wird, aber nicht der Punkt (aus zwei Koordinaten), an dem das geschieht,

• während beim "Schnittpunkt mit der y-Achse" eben der Punkt gemeint ist, nicht aber der y-Wert, bei dem das geschieht

(und nebenbei: in der Alltagssprache sind "Stelle" und "Punkt" fast synonym, ist also auch "Stelle" sozusagen zweidimensional).

Die Ursache für diese Zwiespältigkeit scheint mir eben in der ersten Irritation und der Grundeigenschaft von Funktionen zu liegen:

• eine x-Achse kann sowohl berührt als auch geschnitten werden,

• während die y-Achse wohl geschnitten, aber nicht berührt werden kann.

3. und vielleicht sogar größte Irritation:

• ein Schnitt- bzw. Berührpunkt mit der x-Achse liegt vor, wenn y = 0 ist,

• ein Schnittpunkt                     mit der y-Achse liegt vor, wenn x = 0 ist.

Ist es nach all diesen Irritationen noch ein Wunder, wenn viele SchülerInnen

• andauernd "Nullstellen" und "Schnittpunkte mit der y-Achse" verwechseln,

• nicht wissen, wie sie jeweils berechnet werden (wo man eine 0 einsetzen muss)?

"Nullstellen" und "Schnittpunkte sind

1. nicht nur besonders (relativ) einfach zu berechnen, sondern

2. auch sehr aussagefähig dafür, wo was Entscheidendes "los" ist.

Zu 1., also der einfachen Berechnung:

1. und um mit der besonders einfachen Bestimmung des "Schnittpunkts mit der y-Achse" zu beginnen:

Kriterium für ihn ist, dass x = 0 ist.

Wir müssen also beispielsweise in der Gleichung

y = x² - 2  x - 8

an jeder Stelle, wo bislang ein x steht, nun nur die besonders einfache 0 einsetzen, und erhalten:

y = 0² - 2•0 - 8 =

           =                   - 8

(Hier muss man also gar nicht großartig rechnen!)

Nun haben wir

• schon anfangs als x-Koordinate die 0 festgelegt und

• nun für die y-Koordinate -8 erhalten,

womit sich insgesamt der Schnittpunkt mit der y-Achse als S_y( 0 | -8 ) ergibt.

(Nebenbei: wegen der Funktionseigenschaft kann eine Funktion immer nur höchstens einen Schnittpunkt mit der y-Achse haben.)

2. zur Bestimmung der "Nullstelle" bzw. des "Schnitt-/Berührpunkts mit der x-Achse":

Kriterium dafür ist, dass y = 0 ist.

Wir müssen also beispielsweise in der Gleichung

y = x² - 2  x - 8

für das y vorne jetzt 0 einsetzen und erhalten:

0 = x² - 2  x + 3 .

Die Berechnung, für welche(s) x das der Fall ist, ist nun nicht mehr ganz so einfach - und sei hier nicht vollständig vorgeführt. Vielmehr sei einfach verraten, dass die Gleichung sowohl für x = - 2 als auch für x = 4 erfüllt ist.

Wir können also schon festhalten: die Funktion mit der Funktionsgleichung y = x² - 2  x + 3 hat zwei Nullstellen:

• 1. Nullstelle ist x₁ = -2,

• 2. Nullstelle ist x₂ = 4 .

Wohlgemerkt: die Nullstellen sind Einzel-, nämlich x-Koordinaten.

Nun haben wir

• schon anfangs als y-Koordinate die 0 festgelegt und

• nun für die x-Koordinate -2 bzw. 4 erhalten,

womit sich insgesamt als Schnittpunkte mit der x-Achse S_x1(-2 | 0 ) und S_x2( 4 | 0 ) ergeben:

(Nebenbei: wie hier schon deutlich wird, können Funktionen durchaus mehrere Schnittpunkte mit der x-Achse haben - und zwar bei ganzrationalen Funktionen genau so viele wie der höchste Exponent.
Aber diese Höchstzahl der Schnittpunkte mit der x-Achse muss nicht unbedingt eingehalten werden, da ja ein Funktionsgraph so weit vertikal verschoben sein kann, dass keine oder weniger Schnittpunkte zustande kommen.
Funktionen ungeraden Grades haben aber immer mindestens eine Nullstelle, da sie ja s-förmig von unten nach oben bzw. von oben nach unten gehen.)

Die Schnittpunkte mit der x- bzw. y-Achse sind also wegen Einsetzens der sehr einfachen Zahl 0 besonders (relativ) einfach zu berechnen - und mit ihnen wissen wir nun auch halbwegs, wo die Parabel zur Funktionsgleichung y = x² - 2  x - 8 liegt.

Nun ist ja die Parabel normalerweise noch nicht eingezeichnet, sondern kennen wir nur (inzwischen) die einschlägigen Punkte:

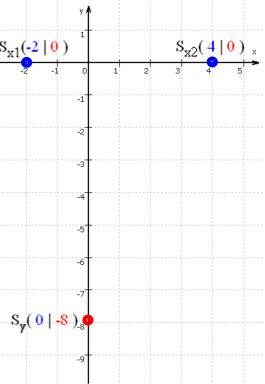
Allein mit den Schnittpunkten mit beiden Achsen und der Vorkenntnis, dass es sich um eine (Normal-) Parabel handelt, ist es zwar nicht ganz einfach, die endgültige Parabel zu zeichnen, aber so halbwegs wird man es hin bekommen.

Nun lässt sich zwar der unterste bzw. "Scheitelpunkt" ebenfalls relativ einfach mittels der sogenannten "Scheitelpunktsform" bestimmen

(was hier ebenfalls nicht detailliert vorgerechnet sei),

und zwar - wie schon die Zeichnung nahelegt - als S(1 | -9). Mit diesem Scheitelpunkt wäre die Parabel besonders einfach zu zeichnen, aber seine Bestimmung über die Scheitelpunktsform hat den Nachteil, dass sie nur für quadratische Funktionen gilt, während die Schnittpunkte mit der x- und y-Achse für alle Funktionen interessante Lageangaben liefern.

(Nebenbei: in der Oberstufe ist es dann möglich, auch für nicht-quadratische Funktionen die "Scheitelpunkte" zu berechnen, die dann allerdings wohlweislich Minima oder Maxima heißen.)

für "Nullstellen" und "Schnittpunkte mit der y-Achse" gilt

1. und sozusagen qua defintionem, dass sie markant sind, denn schließlich liegen sie auf den beiden das Koordinatensystem überhaupt erst konstituierenden Achsen;

2. aber auch - wie gezeigt - , dass sie relativ einfach zu berechnen sind, weil "nur" die einfache Zahl 0 für x bzw. y eingesetzt werden muss.

Dass diese Punkte aber auch "bedeutungsvoll" sind, wird vielleicht erst so richtig an Anwendungen klar, also beispielsweise, wenn man den Unternehmensgewinn (auf der y-Achse) gegen die Zeit (auf der x-Achse) abträgt:

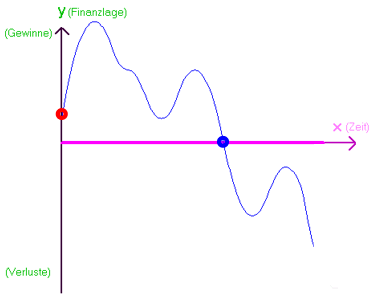
Da sind

• der Schnittpunkt mit der y-Achse, also das Startkapital,

• und die Nullstelle, also der Übergang von Gewinn in Verlust (Konkurs?) bzw. ggf. umgekehrt

doch allemal (für ein Unternehmen) sehr bedeutsame Punkte!

(Nebenbei: die Nullstelle ist nicht der blau markierte Punkt, sondern der Zeit"punkt" [!], bei dem das Unternehmen "in die Miesen" rutscht.)

Und ebenfalls nebenbei: wenn man die (soweit vorhanden) Nullstellen einer Funktion nicht kennt oder nicht ausrechnen kann, so kann man ja dafür sorgen, dass eine Funktion passende Nullstellen und somit auch eine spezifische Lage hat. Vgl. .

Die grundsätzlichen Probleme vieler SchülerInnen mit der Bestimmung von Nullstellen sowie Schnittpunkten mit der y-Achse scheinen mir allerbeste (!) Gründe zu haben:

1. mangelndes Verständnis der Beziehung zwischen (algebraischer) Funktion einerseits und (geometrischem) Funktionsgraph andererseits

(wie erhält man aus ersterer letzteren - und umgekehrt: was sagt letzterer über erstere aus?);

2. mangelndes Verständnis des Koordinatensystems und seiner Quadranten, aber insbesondere Achsen;

3. mangelndes Verständnis des Unterschieds zwischen Koordinaten und Punkten (die aus zwei Koordinaten "bestehen").

Zu 1.:

für das wichtigste, wenn auch nicht Allheilmittel halte ich es,

Funktionen und Funktionsgraphen andauernd aufeinander zu beziehen.

Da können Rechnungen zwar nicht schaden

(und sind manchmal sogar unabdingbar, denn wie sonst soll man überhaupt auf die Idee kommen, dass beispielsweise die Graphen quadratischer Funktionen parabelförmig sind?).

Aber für erheblich wichtiger halte ich dennoch, was hier in diesem Text vorgeführt wird:

"Wie sehen Funktionsgraphen ganz prinzipiell aus und wo liegen sie etwa?"

für mich heißt das auch, dass man schon sehr frühzeitig Funktionsgraphen betrachten kann (und sollte!), deren Eigenschaften man zwar (am Graphen) zwar "sehen", aber  noch lange nicht berechnen kann, ja deren Funktionsvorschrift man sogar nicht mal kennen muss

(warum nicht beispielsweise der Sinus oder Minima/Maxima/Wendepunkte ... bereits in siebten Klassen!?).

Ich meine sogar, dass das "Allgemeinbildung" ist.

Bei all dem können sogenannte "Funktionenplotter", also Programme, in die man den Funktionsterm eingeben kann und die daraufhin den Funktionsgraph zeichnen, wahrhaft nicht schaden. Ihr größter Vorteil ist, dass sie GrundFähigkeiten im Rechnen zwar (hoffentlich) keineswegs überflüssig machen, aber es doch ermöglichen, eine Fülle variierter Funktionen zu betrachten, ohne jede dass man jede haarklein berechnet haben muss. Mittels "Funktionenplotter" sind also erheblich mehr Funktionen "diskutierbar" als die ganz wenigen, die man sonst an der Tafel schafft.

Allerdings haben die üblichen "Funktionenplotter" auch entscheidende Nachteile:

1. die automatische Umsetzung von Funktionsgleichungen in Funktionsgraphen ist

   (zumindest dann, wenn die "Funktionenplotter" zu früh eingesetzt werden)

   oftmals allzu suggestiv;

2. man muss die Funktionsgleichung schon kennen (eingeben können), um den zugehörigen Graphen angezeigt zu bekommen;

3. zwar gibt es auch "Funktionenplotter" mit der Möglichkeit, Parameter zu verstellen (beispielsweise die Steigung), aber diese Parameterverstellung ist oftmals viel zu kompliziert, statt dass sie einfach mit Schiebereglern funktioniert oder - noch besser - direkt am Graphen bzw. in der Funktionsgleichung vorgenommen werden kann (sprich ).

Vgl. etwa ein Programm, das vor einigen Jahren einer meiner Schüler (Robert Hohm) erstellt hat:

 

Zu 2., also "mangelndem Verständnis des Koordinatensystems und seiner Quadranten, aber insbesondere Achsen":

Hier muss man z.B. (immer wieder) durchnehmen, d.h. man darf das Koordinatensystem nicht als selbstverständlich "verkaufen"

(was es offensichtlich für viele SchülerInnen auch nicht ist!).

Und auch ansonsten gilt: "(nur) steter Tropfen höhlt den Stein", d.h. es muss den SchülerInneN immer wieder verdeutlich werden:

(und was ist dann wohl auf den jeweiligen Achsen los?)

Denkbar wäre da auch ein Computerprogramm, bei dem man mit dem Mauszeiger über alle Quadranten eines leeren (!) Koordinatensystems fahren kann, wobei immer die x- und die y-Koordinate des jeweiligen Punktes S (x | y ) angezeigt wird und die Vorzeichen markant farbig hervorgehoben werden bzw. wechseln.

Und an dieses Programm würde jedeR SchülerIn

"zwangsweise" (und notfalls wiederholt) gesetzt, die/der wieder mal was nicht "gerafft" hat.

(Natürlich reicht "Davorsetzen" alleine nicht, sondern solche SchülerInnen hätten in einem Protokoll zu beschreiben, was sie da sehen bzw. erkennen.)

Oder eine weitere Programm-Möglichkeit: im Ursprung ist eine Art Uhrzeiger befestigt, den man über die Quadranten und Achsen drehen kann, wobei diese jeweils in einer spezifischen Farbe eingefürbt werden und nur die jeweiligen Vorzeichen angezeigt werden, also z.B. im ersten Quadranten "x + , y +" .

Im Hinblick auf unser "Schnittpunkte-mit-den-Achsen-Problem" wäre auch ein Computerprogramm ähnlich dem von Robert Hohm denkbar, bei dem man die Schnittpunkte (vorgegebener, sich dabei aber natürlich verändernder Funktionsgraphen) ziehen kann - und dabei die Koordinaten angezeigt werden, die natürlich immer entweder im x-Wert oder im y-Wert 0 sind.

Zu 3., also "mangelndem Verständnis des Unterschieds zwischen Koordinaten und Punkten":

Man kann nicht oft genug durchnehmen, wie überhaupt die x-y-Zuordnung "um die Ecke" (vgl. ) stattfindet und dass sich jeder Punkt aus seinen beiden Koordinaten zusammensetzt.

Auch hier wäre ein Computerprogramm denkbar, nämlich eines, bei dem man wieder einen Mauszeiger über ein leeres Koordinatensystem zieht und

1. an der x-Achse der x-Wert,

2. die "um die Ecke"- Zuordnung zum y-Wert,

3. an der y-Achse der y-Wert

4. und am Punkt S ( x | y ) angezeigt würde

(ansatzweise umgesetzt ist das im Modul "Punkte in der Ebene" in ).

Vielleicht viel besser (weil handgreiflicher) ist es, wenn man all das mit Bändern auf dem karierten Boden des Klassenraums übt.

Oder man lasse ein neckisches "Koordinatensystem-Spiel" spielen (und spiele mit!):

Spiegelregeln:

1. Jeder Spieler beginnt mit einer Figur beim Ursprung 0 und würfelt nacheinander mit zwei Würfeln.

2. Die Augenzahl des ersten Würfels wird nach rechts (in x-Richtung), die Augenzahl des zweiten nach oben (in y-Richtung) gegangen.

3. Wenn eine Figur gegen eine "Balustrade" knallt, ändert sich (bis zur nächsten Balustrade) die Laufrichtung. Ein Beispiel:

Angenommen, eine Figur steht bereits in D, und der Spieler würfelt nun erst eine 5, dann eine 4. Dann muss die Figur

• erst 2 Schritte nach rechts bis gegen die Wand gehen,

• dann die restlichen 3 Schritte wieder nach links,

• und dann 4 Schritte nach oben, bis er in E ankommt.

(entsprechend kann sich die Laufrichtung

• an der linken Balustrade wieder nach rechts

• und an der oberen nach unten

• bzw. der unteren wieder nach oben umkehren).

4. Ziel des Spiels ist es, die Figur in einen der Punkte A, B oder C zu bringen, wobei man nicht genau dort zum Stillstand kommen muss, sondern es reicht, durch die Punkte "durchzugehen".

Man kann auch Pech haben und wieder im Ursprung 0 landen, woraufhin man von vorne anfangen muss.

5. Eine (gegnerische oder eigene!) Figur, die dort steht, wo ein Spieler gerade "landet", fliegt raus und muss in 0 wieder von vorne anfangen.

6. Denkbar wäre es, dass jeder Spieler - wie in "Mensch ärgere dich nicht" - vier Figuren hat und jeweils dann eine neue Figur in Spiel bringen darf, wenn der erste seiner beiden Würfelwürfe eine 6 ist.

In dieser ersten Version muss immer erst der erste und dann der zweite Würfelwurf "gegangen" werden (immer x vor y).

In einer später
en Variante könnte man dann allerdings auch erlauben, dass ein Spieler sich aussuchen darf, welche der beiden Zahlen er in welche Richtung gehen möchte - was den Vorteil hätte, dass man nicht mehr völlig von den zufälligen Würfelwürfen abhängig wäre, sondern strategisch vorgehen könnte.

Eine weitere nette Variante mit sechs Zielpunkten wäre

Und noch ein Vorschlag: ein Programm oder besser noch ein "handgreifliches" Modell, auf dem man nacheinander

1. erst die x-Werte,

2. dann die y-Werte,

3. zuguterletzt beide auf einmal

verschieben kann, und zwar folgendermaßen: