Orientierung in Ebene und Raum

vgl.       "Süden ist da, wo ich stehe und meine, dass Süden ist." (E.W.) (Vgl. „Chuck Norris trägt keine Uhr. Er entscheidet, wie spät es ist.“) Ich halte räumliches Orientierungsvermögen keineswegs nur im Geometrieunterricht für unabdingbar, bzw. die Geometrie ist auch deshalb besonders wichtig, weil da solches Vermögen auch für andere mathematische Gebiete geübt wird. "Aus der Forschung [???] weiß man, dass jemand, der nicht rückwärts gehen kann [was bei so einigen Grundschulkindern der Fall zu sein scheint], auch nicht zählen kann, nicht einmal vorwärts [...]" (zitiert nach ) orientieren "jemanden von etwas unterrichten", meist reflexiv im Sinne von "sich zurechtfinden; sich umsehen, sich erkundigen, sich unterrichten; sich nach jemandem, nach etwas ausrichten, sich auf jemanden, auf etwas einstellen": Das Verb wurde im 18. Jh. aus gleichbed. frz. [s']orienter, einer Bildung zu frz. orient "Sonnenaufgang, Osten; Orient" (< lat. oriens, Orient), entlehnt. Auszugehen ist dabei von einer ursprünglich geographischen Bed. "die Himmelsrichtung nach dem Aufgang der Sonne bestimmen". - Das vom Verb abgeleitete Substantiv Orientierung "Kenntnis von Weg und Gelände; geistige Einstellung, Ausrichtung" ist seit dem 19. Jh. belegt. (Duden) "Bei den nordaustralischen Ureinwohnern des Stammes der Guugu Yimithirr richtet sich [laut Forschungen der Max-Planck-Gesellschaft für Psycholinguistik] die räumliche Orientierung ausschließlich nach absoluten Koordinaten, nämlich den vier Himmelsrichtungen. Ein Messer liegt bei ihnen nicht rechts vom Teller, sondern beispielsweise östlich oder südlich, je nach Lage des Hauses. Befindet sich ein Gegenstand nach unserem Beschreibungssystem in der linken Hosentasche einer Person, würde eine Guugu Yimithirr diesen beispielsweise als in seiner westlichen Hosentasche befindlich beschreiben; dreht er sich um 1800 auf seiner Achse, ist der Gegenstand dann in seiner östlichen Hosentasche. Dieses sehr genaue und eindeutige System setzt aber voraus, daß das Unterbewußtsein einer Person jede Bewegung der eigenen Person aber auch seines Umfeldes stets genau registriert und nachrechnet, um spontan eine Ortsbestimmung vornehmen zu können. Bei wissenschaftlichen Untersuchungen dieser verblüffenden Fähigkeit stellte sich heraus, daß der Orientierungssinn einer Brieftaube wesentlich schlechter und fehlerhafter ist, als der eines Guugu Yimithirr. Das Argument, die Verarbeitung würde nicht unbewußt, sondern bewußt durch Orientierung am Himmels-/Sternenstand erfolgen, gilt auch als entkräftet. Der schlagkräftige Beweis besteht darin, daß die Guugu Yimithirr sich sogar nachts in geschlossenen, dunklen und ihnen unbekannten Räumen perfekt orientieren können." (zitiert nach ) Mit diesen Befunden sind evtl. auch die erstaunlichen navigatorischen Fähigkeiten der polynesischen Völker erklärbar.

Um vom Großen (d.h. auch: den hübschen Schlagworten) aufs Kleine zu kommen: wenn es (vor allem Fachlichen, das da "nur" wichtigstes Handwerkszeug ist) vornehmste Aufgabe von Schule ist, den SchülerInnen Möglichkeiten (verschiedenste Denk- und Handlungsmodelle) anzubieten, 

sich selbstständig in einer multidimensionalen und pluralistischen (?) Welt zu orientieren,

so gehört dazu auch, die Metapher „Orientierung“ wieder wörtlich (d.h. geometrisch!) zu nehmen:

Orientierung [...] das Sichzurechtfinden im Raum.

(Duden)

Trotzdem möchte ich die metaphorische und die wörtliche Bedeutung natürlich nicht simpel gleichsetzen: es gibt Menschen, die bestens „im Leben zurecht kommen“, obwohl sie doch völlig unfähig sind, sich räumlich zu orientieren ^[1]  

(und dennoch kommen sie immer [durchaus räumlich] an, indem sie andere Strategien anwenden, also z.B. Passanten fragen).

Unverzichtbar scheint mir geometrische Orientierung allerdings in der Mathematik.

Leider wird diese geometrische Orientierungskompetenz aber gerade in der üblichen Schulmathematik allzu sehr unterschätzt bzw. viel zu wenig trainiert: gerade bzw. ausgerechnet in der Geometrie kommt man vor lauter Rechnen und Konstruieren nicht zur Anschauung.

Ein Musterbeispiel ist da für mich die Kongruenzgeometrie (vgl. auch ). Was da in Schulen betrieben wird („drehe, spiegele und verschiebe dann noch mal - und zwar immer auf Papier und mit Zirkel und Lineal“) fürdert nicht die Grundanschauung, sondern zerstört geradezu das allzu Banale:

wenn ich z.B. ein Buch Buch schwenke (es drehe), es auf einem Tisch hin- und herschiebe, auf die Vorderseite lege (spiegele) oder gar – in komplexen Bewegungen - alles gleichzeitig tue, also mit ihm rumwedele, verändert das Buch „natürlich“ nur seine Lage, nicht aber seine Form.

(und nebenbei: die Kongruenz wird erst interessant, wenn man gleichzeitig auch ihr "Gegenteil", nämlich die Ähnlichkeit, durchnimmt, bei der die Form [Größe] sich ändert und doch irgendwie [wie?] "ähnlich" bleibt; die beiden Themen "Kongruenz" und "Ähnlichkeit" werden in der Schulmathematik aber leider weit auseinander gehalten.)

oder: zwei Gegenstände A und B sind kongruent, wenn

- A völlig B verdeckt UND

- B völlig A verdeckt.

Warum tut man nicht (erst mal) genau das: reale Dinge drehen, verschieben und spiegeln sowie hintereinander verstecken?

(Warum zerdeppert man zu Beginn der Bruchrechnung nicht echtes Porzellan in Bruchstücke?)

Damit meine ich keineswegs

• eine simple Anwendungsmathematik (eine Mathematik, die bei den [vermeintlichen] Anwendungen stehen bleibt): nein, auch reine Innermathematik ^[2]

(vgl. etwa unten Kegelschnitte; und wo in der [Schüler-] Realität gibt's schon ernsthaft Kegelschnittanwendungen?)

will und kann veranschaulicht und erfahren werden;

• ein Stehenbleiben bei reiner Anschauung: im Gegenteil können sich aus der Anschauung ja überhaupt erst (und dann durchaus motiviert) mathematische Fragen ergeben:

ich bin der festen Überzeugung, dass simpelste räumliche Orientierung (wie auch wieder anhand der Kegelschnitte klar wird) durchaus auch in der Oberstufe Platz hätte – und zu mathematischen Fragen führen könnte, die allemal eines Leistungskurses würdig wären.

Diese räumliche Orientierung wird ja implizit überall verlangt – nur leider viel zu wenig geübt:

• sowieso in der Vektorgeometrie

(„eine Kugel schneidet eine Ebene“: eine mit geradezu tödlicher Sicherheit vorkommende Aufgabe in der Vektorgeometrie, mit der viele SchülerInnen dennoch nichts anfangen können, weil sie damit nicht die mindeste Anschauung verbinden, denn wo kommt sowas im "richtigen" Leben schon vor - außer beim Saturn

und jenen - wie irre komisch! - ominösen Golfbällen ("ich spiele Golf und werde demnächst in die FDP aufgenommen"), die mitten in einem Autofenster stecken geblieben zu sein scheinen?:

Offensichtlich ist der Effekt enorm attraktiv, weil ästhetisch. Warum? Vielleicht doch wohl, weil sich da so recht platonisch das perfekt Gerade [die Ebene] und das perfekt Runde [die Kugel] begegnen. Noch schöner aber ist der Effekt, wenn die Kugel kontinuierlich durch die Ebene "flutscht"; ein Effekt, der dem alten Menschheits-Entgrenzungstraum gleichkommt, durch Wände gehen zu können);  

(Ich sehe durchaus die technischen Schwierigkeiten; dennoch sei mal provokativ gefordert: in der dreidimensionalen Vektorgeometrie darf überhaupt keine Aufgabe durchgenommen werden, zu der kein Modell vorhanden ist bzw. gebastelt wird. Bzw. Abstraktion [Arbeit im Kopf ohne Modell] sollte immer nur - durchaus wichtiges! - Endziel sein.)

• genauso wird Orientierungsfähigkeit aber – nur nicht so deutlich sichtbar – in der Analysis(und da mehr in der Ebene als im Raum) verlangt . Gerade da aber zeigt sich doch: viele SchülerInnen rechnen ohne Sinn und Verstand (und kommen dann natürlich auch auf die abstrusesten Ergebnisse), weil sie nicht die mindesten geometrischen Vorstellungen haben bzw. sie sich nicht vorher machen:

„eine Funktion 3. Grades muss eine Nullstelle haben, und wenn ich keine rauskriege, kann irgendwas nicht stimmen.“

Oder was heißt denn schon (ursprünglich bei Newton) "Ableitung": doch wohl die gar nicht so einfache Orientierung in Raum und Zeit!

Wir Lehrerinnen bewerten scheinbar nur (durchaus oft geübte!) "Rechenfähigkeit", in Wirklichkeit aber oftmals mindestens ebenso sehr auch (selten oder gar nie geübtes) räumliches Orientierungsvermögen(etwa so, wie Deutschlehrer implizit immer Ausdrucks- und historisch-soziales Differenzierungsvermögen voraussetzen).

Selbstverständlich sollte geometrische Orientierung in der (zweidimensionalen) Ebene anfangen und dann erst auf den (dreidimensionalen) Raum übergehen:

• wo ist oben und unten, links und rechts, Nord und Süd und Ost und West

(„wie man nach Peking kommt? Ganz einfach: sobald man in Russland reinkommt, einfach rechts halten“)

sowie die x- und y-Achse?

  (und - s.u. - wo befinde ich mich bzgl. einer Sache?)

• wie gebe ich jemandem, dem ich beispielsweise den Weg in Stadtzentrum zeigen will, eine Grundorientierung?
• was sind wichtige und was nebensächliche Landmarken?

Der (dreidimensionale) Raum ist sowieso ein Problem, sobald man nur zweidimensionale Projektionen von ihm (an der Tafel, im Schulbuch und Heft) betrachtet

(und man sollte sich eingestehen: ausnahmslos jeder hat Probleme mit zweidimensionalen Projektionen des dreidimensionalen Raums!).

Es ist doch schlichtweg ein Widersinn, wenn man mit diesen zweidimensionalen Projektionen anfängt – und aufhört. Da kann ich nur sagen: massenhaft (dreidimensionale, handgreifliche) Modelle tun Not – und sollten allemal am Anfang aller Raumgeometrie stehen, bzw. alle Ergebnisse aus zweidimensionalen Projektionen sollten, wenn irgend möglich, am Ende wieder an dreidimensionalen Modellen überprüft werden.

(Dabei will ich ja gar nicht bezweifeln, dass zweidimensionale Projektionen durchaus ihren Wert haben, nämlich Abstraktion üben; vgl. )

Wie schon gesagt: die eigentlich mathematischen Fragestellungen sollen ja keineswegs ausgeschlossen werden. Und dennoch sollten sie lange Zeit zurück stehen. Die SchülerInnen sollten erstmal und immer wieder stunden- und wochenlang basteln und rumhantieren, schieben und drehen und durchschneiden usw., ohne dass ein im engeren Sinne mathematischer Ansatz vorkäme.

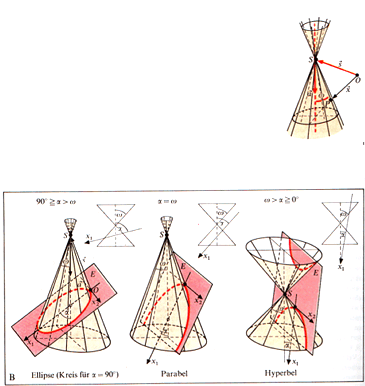
Nehmen wir nur mal die Kegelschnitte: je nachdem, wie man einen Kegel durchschneidet, ergibt sich

1. ein Kreis,

2. eine Ellipse,

3. eine Parabel,

4. eine Hyperbel:

(ich habe diese Zeichnungen mangels Masse aus einem Universitätsbuch geklaut, das natürlich einen erheblich theoretischeren Ansatz hat; z.B. stört ja – für SchülerInnen – schon allein der [für die theoretische Mathematik durchaus wichtige] Doppelkegel)

Das ist doch wirklich erstaunlich, dass sich diese völlig verschiedenen Dinge (Kreis, Ellipse, Parabel, Hyperbel) aus ein und demselben Ding (Kegel) ergeben! Woher „wusste“ der Kegel das?

Das erinnert mich doch an Michelangelo, der mal so etwa sinngemäß und durchaus demütig gesagt hat, nicht er schaffe Skulpturen, sondern er hole sie nur aus dem Stein heraus (in dem sie schon angelegt bzw. vorgegeben waren).

Und dieses „Wissen“ des Kegels nachzuvollziehen, also herauszufinden, weshalb da die verschiedenen Figuren herauskommen, ist schon echte Hochmathematik. Nur meine ich: diese „richtige“ Mathematik kann ja immer noch kommen (und sollte – zumindest ansatzweise – irgendwann kommen!).

Aber man kann doch auch gleichzeitig viel einfacher anfangen (schon in einer 5. Klasse): Styroporkegel (und andere Styroporkörper) verteilen und einfach durchschneiden lassen. Die SchülerInnen werden allemal staunen, was da alles bei raus kommen kann (auch wenn sie natürlich noch nicht Parabeln und Hyperbeln unterscheiden bzw. gar mathematisieren können).

Denn staunenswert ist die Ästhetik ^[3]der herauszufindenden Kurven allemal!: ein Kreis, eine Ellipse, eine Parabel ist intuitiv schön, auch wenn man sie noch gar nicht benennen geschweige denn formalisieren kann

(und dennoch ist mit dieser Ästhetik schon die Motivation vorhanden, sie auch irgendwann zu formalisieren) .

An solch einem Kegel lässt sich tatsächlich massenhaft geometrische Orientierung üben.

Da reicht es allemal nicht

(obwohl das ja „state of the art“ im gängigen Mathematikunterricht ist),

1. entweder einige ganz wenige Schnitte vornehmen zu lassen
2. oder aber (und noch simpler bzw. einfallsloser) einige wenige fertige Zeichnungen (s.o.) zu geben

(die SchülerInnen also nichtmal selbst schneiden zu lassen: denn warum heißen diese Dingens denn wohl Kegelschnitte?!).

Bei beiden Vorgehensweisen wird den SchülerInnen nämlich Elementares gestohlen:

• die Eigenerfahrung, das eigene Tun, die eigene erste Entdeckung;
• die tatsächlich körperliche "Handgreiflichkeit" bzw. wortwörtlich visuelle „nackte Anschauung“: wenn man den Kegel z.B. horizontal durchschneidet, liegt  tatsächlich ein Kreis vor einem

(in einer Zeichnung/zweidimensionalen Skizze aber fatal irreführend eine Ellipse!)

• die Übergänge: wie der Kreis in eine Ellipse(der Kreis als seltener Spezialfall bzw. "Grenzwert" der Ellipse) und diese „urplötzlich“ (ein Mathematiker würde sagen: polstellenartig) in eine Parabel aufreißt.

Und da dann sind (ausnahmsweise!) wirklich mal Computerprogramme angesagt, die allein eine kontinuierliche Bewegung der Schnittrichtung vorführen und damit „bewegte Mathematik“ ^[4] (vergleichbar. etwa der Schichten-Computertomographie eines Körpers) zeigen können.

Solche Computerprogramme bereiten aber das im Grunde Allerwichtigste vor:

• dass SchülerInnen sich „im Kopf“ durch einen Körper (in diesem Fall Kegel) „bewegen“ können (als würden sie da "endoskopisch"  selbst durchtauchen, als wären sie selbst die Schnittebene): also mathematische  

Abstraktion = Anschauung !

---

Gerade als Mathematiker mit einer bestimmten (einseitigen?) Denkweise muss man sich im Klaren darüber sein, dass die eigene Orientierungsweise

• nicht die einzig mögliche

• und damit eventuell schwer (wenn überhaupt) zu vermitteln ist.

Während "unsereins" sich immer in glasklar raumzeitlichen Koordinaten bewegt

(z.B.

• sogar in geschlossenen Räumen weiß, wo welche Himmelsrichtungen liegen,
• ein fast untrügliches Gespür dafür hat, wieviel Uhr es ist,
• eine Autokarte "genordet" lesen kann, sie also nicht so drehen muss, wie man selbst gerade fährt),

ist das bei anderen keineswegs selbstverständlich: sie leben in einer ganz subjektiven Raumzeit, d.h. alles ist (wie bei kleinen Kindern?) um sie selbst zentriert:

• vgl. oben: "Süden ist da, wo ich stehe und meine, dass Süden ist", d.h.
• es gibt überhaupt keine von der Person unabhängigen Himmelsrichtungen, sondern nur vor/hinter/links von/rechts von mir
  (da merkt sich jemand als Parkplatz in einer fremden Großstadt: "hinter dem roten LKW" - auch wenn der zwei Stunden später längst weggefahren sein mag),
• "früh", "spät", "gleich" und "sofort" sind ganz subjektive Begriffe.

Wie soll man solchen Menschen die "objektiven" mathematischen Koordinaten vermitteln? Geht das überhaupt, oder sind da prinzipielle Grenzen erreicht?

Solch prinzipielle Grenzen mögen fatal im Hinblick auf das Lernen von Mathematik sein. Ansonsten kann man sich aber doch probeweise mal fragen, wer da eigentlich einen "Schaden" hat: beispielsweise

• derjenige, der sich komplett dem neuzeitlichen Zeitraster angepasst hat
  (eine Uhr verschluckt hat bzw. längst selbst eine ist),
• oder derjenige, der noch ein eigenes, situatives Zeitempfinden hat?

---

Es gibt so unendlich viele Möglichkeiten, geometrische Orientierung zu üben.

Ich möchte hier nur ein Beispiel andenken:

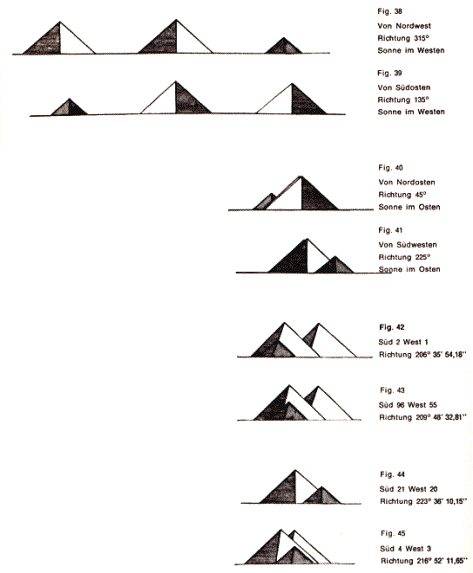
• die jedem bekannte Irritation dadurch, dass ein und derselbe Gegenstand aus verschiedenen Richtungen ganz anders aussieht

(so dass man den einen Gegenstand darin kaum wiederzuerkennen vermag).

• allemal faszinierend (weshalb auch immer) sind die ägyptischen Pyramiden in Gizeh.

Es gibt verschiedenste und nach wie vor höchst umstrittene bzw. kontroverse Theorien über diese Pyramiden.

Z.B. wird da diskutiert, ob die Pyramiden

• durch schlimmste Sklavenarbeit oder
• letztlich doch „freiwillig“ (also zu einem überzeugenden „höheren“ Zweck)

erstellt worden seien.

(Nebenbei: das Thema wäre ja mal ein hübscher Anlass, ansatzweise – und zwar ausgerechnet mitten im Mathematikunterricht! - in die Kultur ^[5] einer unserer [auch mathematisch!] wichtigsten Vorgängerzivilisationen einzuführen!)

Zwei andere Thesen zu den Pyramiden in Gizeh:

• dass diese Pyramiden wirklich nur bombastisch-grandiose Grabmäler seien,
• dass die Grabmale nur ein Vorwand bzw. eine Täuschung seien, es in „Wirklichkeit“ aber um viel Wichtigeres bzw. Elementareres gegangen sei: Astronomie, aber vor allem (im damaligen Ägypten lebenswichtige!) Landvermessung = Geo(Erde)metrie(Messung).

Wahrscheinlich ist (wieder mal) die Ausschließlichkeit falsch. Nehmen wir aber dennoch mal letztere (die geometrische) These probeweise mal ernst:

Ägypten ist und war schon immer zu 99 % ein Wüstenland, und nur in der direkten Nachbarschaft des Nils gibt es (enorme!) Fruchtbarkeit, d.h. Lebensmöglichkeiten für Menschen. Der Grund für diese Fruchtbarkeit: die Schlammmassen, die jedes Jahr aus dem Oberlauf des Nils kommen und die Felder am Nil entlang überschwemmen.

Nur liegt genau in diesem Vorteil auch das Problem: diese enorm fruchtbaren Schlammmassen überschwemmen ausnahmslos alles Land.

Für die damaligen Ägypter ergaben sich daraus – so sagt man zumindest – zwei Probleme:

1. vorherzusagen bzw. zu warnen, wann diese Überschwemmung kommen würde (also ein Kalender, womit als vierte Dimension auch die Zeit ins Spiel kommt!);
2. , auch nach einer Überschwemmung wieder (Privatbesitz-?)Grenzen feststellen zu können.

Im 2. Fall brauchte man also schlichtweg geometrische Orientierung, und es wird gesagt, genau da habe die Geburtswiege sämtlicher abendländischen Geometrie gestanden!:

 Geo-Metrie = Erd-(ver-)Messung

Eine weitere These ist, dass die Pyramiden nur deshalb errichtet worden seien, weil sie mit ihrer enormen, bei gutem Wetter über hundert Kilometer hinweg erkennbaren Größe (und wegen ihrer Spitzen aus massivem Gold) überhaupt erst die dringend benötigte Orientierung ermöglicht hätten.

Und da sind wir wieder beim o.g. Problem: wie kann man erkennen, wo man sich bzgl. der Pyramiden befindet?

Das ist ja nur eine Perspektive. Aus anderen Perspektiven sehen diese drei Pyramiden allemal anders aus:

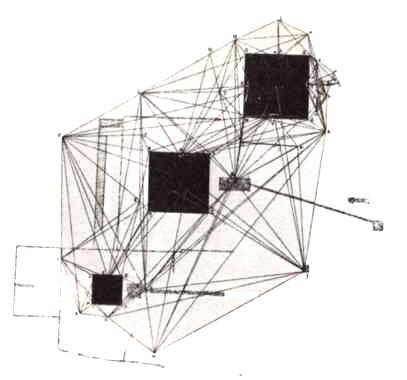
Die exakte Bestimmung der Lage der drei Pyramiden zueinander (und der jeweiligen Richtung, in der man sich bzgl. ihrer befindet) ergibt enorme(SchülerInnen allemal überfordernde!) mathematische Probleme (sogenannte „Triangulation“):

Aber ich glaube dennoch, dass es sich allemal lohnt, sich mit den SchülerInnen probeweise(unmathematisch) zwischen diesen Pyramiden zurecht zu finden, und dass es die SchülerInnen interessieren würde.

Ich weiß auch, dass schon allein die erste räumliche Orientierung keineswegs einfach ist:

• auch ich (und so begabt bin ich nun auch wieder nicht) habe da meine lieben Schwierigkeiten;
• und von wegen der drei Pyramiden: sämtliche Physiker und Mathematiker dieser Welt haben bisher das im Grunde doch ganz simple Dreikörperproblem nicht lösen können:

• wie sich die Gravitationen dreier (oder mehrerer) Körper (z.B. Planeten) zueinander verhalten;
• wie dann die exakten Bewegungen/Umlaufbahnen dieser drei Körper aussehen.

Aber genau das ist ja der Vorteil: genauso dumm zu sein wie alle. 

Man arbeite aber wieder so praktisch wie irgend möglich, d.h.

• rekonstruiere beispielsweise aus mehreren Fotos  

(was gar nicht so einfach ist, sondern überhaupt erst mitten ins Problem führt)

den Lageplan

(und gebe ihn nicht vor),

• baue dann die Pyramiden im Modell nach
• und betrachte dieses Modell von allen Seiten.

Und hinterher kann man dann ja - wo wir schon so gerne rumsäbeln - auch noch (Styropor-)Pyramiden durchschneiden

 (und z.B. die erstaunliche, von einer theoretischen Pyramide ja durchaus interessant abweichende Geometrie

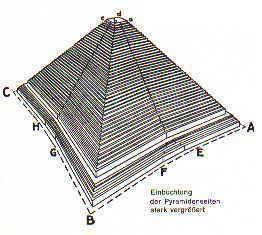
der Cheops-Pyramide durchnehmen) .

Ich halte es also für durchaus sinnvoll, ja sogar dringend geboten, den mathematischen Stoff an anderer Stelle erheblich zu beschneiden und dafür ganze Wochen und Monate mit möglichst praktischer Orientierung in der Natur, schnibbelnd und schneidend, durch Blinde-Kuh-Spielen oder Gedankenreisen durch geometrische Körper zu verbringen, also ausdrückliche Unterrichtseinheiten allein zur räumlichen Orientierung zu erarbeiten.

---

[1] vgl. auch „Der Mann im Mond“

[2] vgl. „Innermathematische Veranschaulichung“

[3] vgl. „Ästhetik der Mathematik“

[4] vgl. „Newtons bewegte Mathematik“

[5] vgl. „Mathematik als KULTURwissenschaft im Unterricht“