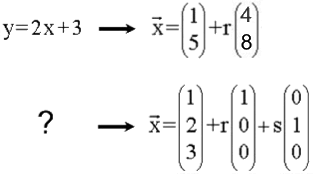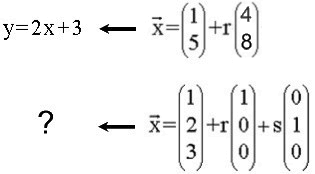
In der Analysis sieht eine Geradengleichung z.B. so aus:

g: y = 2 x + 3

In der Vektorgeometrie sieht eine Gerade hingegen z.B. so aus:

g:

Da stellt sich die dreifache Frage,

• ob und wenn ja wie man eine analytische in eine vektorielle Geradenform überführen kann - und umgekehrt,
• wie die Geradengleich ein und derselben Gerade
  • in der analytischen
  • in der vektoriellen Geradenform

aussieht,

• ob man vielleicht sogar der analytischen Geradenform ansehen kann, wie ihre vektorielle Geradenform aussieht - und umgekehrt; ob also die wechselseitigen Umformungen

• einfach und intuitiv möglich sind

(etwa so, wie man sofort sieht, dass 2 und unterschiedliche Schreibweisen für dieselbe Zahl sind; aber schwieriger ist es schon zu sehen, dass auch 2 und dieselbe Zahl sind) 

• oder großartiger Rechnungen bedürfen und abstrakt bleiben

(vgl. etwa die beiden [?] Zahlen 0,25 und , die völlig unterschiedlich aussehen und doch nur verschiedene Schreibweisen derselben Zahl sind).

Fangen wir mit Letzterem an: die Zeile

 

signalisiert ja schon etwas Doppeltes:

1. dass die analytischeeForm g: y = 2 x + 3 und diee vektorielleeForm g:: tatsächlichh

(wie hier auch die Verwendung(wie hier auch die Verwendung desselben Geradennamens "g" signalisiert)

 dieselbe Gerade g beschreiben,

2. dass - dargestellt durch den abwechselnd nach links bzw. rechts verweisenden Pfeil - beide Formen tatsächlich ineinander überführbar sind.

Die Frage bleibt vorerst aber, ob man der analytischen Form g: y = 2 x + 3 ansehen kann, dass ihre vektorielle Form  g: lautet bzw. lauten muss

(oder umgekehrt).

Ein Vergleich der Zahlen in beiden Formen zeigt zu allererst, dass keine einzige Zahl der einen in der anderen Form vorkommt. Und arg spitzfindig erscheint die Feststellung, dass immerhin

• die Division der beiden Zahlen 8 und 4 aus dem Richtungsvektor der vektoriellen Form
• die Steigung 2 aus der analytischen Form ergibt

(und doch ist das eine wichtige Feststellung).

Fragt sich nur, wie ich dafür gesorgt habe, dass die beiden Formen g: y = 2 x + 3 und g: dieselbe Gerade darstellen

(und dann in einem zweiten Schritt, dass man das nicht sofort erkennt).

Ausgegangen bin ich von der analytischen Form g: y = 2 x + 3, in der 2 die Steigung und 3 der y-Achsenabschnitt ist

(man fange beim Zeichnen immer mit dem y-Achsenabschnitt an!):

 

Von dem so erhaltenen Punkt S ( 3 | 0 ) aus gehen wir nun um 1 nach rechts und um die Steigung 2 nach oben:

Durch S ( 3 | 0 )  und den neu erhaltenen Punkt R ( 1 | 3 + 2 ) = R ( 1 | 5 ) legen wir nun die Gerade g:

Nun brauchen wir nur noch zwei Strecken durch Vektoren zu ersetzen:

 

Damit erhalten wir die vektorielle Form

g: ,

der man an den beiden Zahlen 3 und 2 noch sehr schön ihre Herkunft von g: y = 2 x + 3 ansieht.

Wir erhalten also

y = 2 x + 3     

oder allgemein:

y = mx + n      

(Hier liegt nebenbei ein typische mathematische Problem vor:

1. lernt man sowas auswendig,
2. oder leitet man es sich gegebenenfalls jeweils kurz her?

Es kommt halt darauf an, ob man es häufig [a.] oder selten [b.] braucht. 

Ich befürchte allerdings, dass viele SchülerInnen es sich nur für die nächste Klausur in den Kopf reinknallen - und danach umgehend vergessen, da es ja später in der Tat kaum wieder vorkommt.

Bzw. wenn es später doch nochmals vorkommt, kann man als Lehrer von vorne anfangen, da es ja vollständig vergessen wurde - und sowieso nicht verstanden.

Da ist es mir manchmal lieber, dass die "Denkweise", mit der man "drauf" kommt, verstanden wurde - und die Formel erst gar nicht auswendig gelernt wird.

Vor allem aber gibt es beste Gründe, sich die Umformung falsch zu merken:

• wo gehört in der vektoriellen Form die 0 und wo gehört die 1 hin?
• kommen m und n in der vektoriellen Form nach oben oder unten?
• 

Es wäre also allemal gut, wenn die vektorielle Form immer noch kurz an der Anschauung

gemessen würde.) 

Im konkreten Fall haben wir

y = 2 x + 3     

erhalten, während oben

 y = 2 x + 3     

behauptet bzw. suggeriert wurde.

Und das scheint sich doch gewaltig zu widersprechen, denn es sieht doch schwer danach aus:

      

Hier begegenen wir einem kleinen Problem:

• während es in der Analysis nur eine einzige Gleichung für eine gegebene Gerade gibt

(man könnte y = 2 x + 3 höchstens mit Brüchen darstellen, also z.B

,

aber das würde man ja wieder umgehend kürzen),

• kann ein und dieselbe Gerade in der Vekorgemetrie auf völlig unterschiedliche Weisen ausgedrückt werden, je nachdem
  • wo ich mit dem Stützvektor auf die Gerade gehe

(wo ich auf die Autobahn fahre), 

• welche Orientierung und Länge der Richtungsvektor hat

(in welche Richtung der Autobahn und mit welcher Geschwindigkeit ich fahre; Hauptsache, es ist dieselbe Autobahn).

Hier wird also behauptet, dass   und dieselbe Gerade g beschreiben.

Wenn die beiden Formen auch auf den ersten Blick völlig unterschiedlich aussehen, so kann man doch durch gründlichen Koordinatenvergleich herausfinden:

• 0 + 1 =1 und 3 + 2 = 5, d.h. : der neue Richtungsvektor ist die Summe des alten Stützvektors und des alten Richtungsvektors;
• 4 • 1 = 4 und 4 • 2 = 8, d.h. : der neue Richtungsvektor ist einfach viermal so lang wie der alte.

Oder anschaulicher:

• ich gehe nicht mehr mit auf die Gerade g, sondern mit  ,
• und ich gehe auf ihr viermal so "schnell":

Aber es bleibt natürlich dieselbe Gerade g !

Für die Umwandlung

analytische Geradenform → vektorielle Geradenform

kann uns das aber alles egal sein: es reicht

y = 2 x + 3   →  

bzw. allgemein

y = mx + n   →    ,

und wir müssen nicht wissen, dass die analytische Geradenform auch in eine andere vektorielle Geradenform überführt werden muss.

Komplizierter ist's allerdings im umgekehrten Fall, also für

analytische Geradenform ← vektorielle Geradenform.

Oder genauer: das ist noch ganz einfach, wenn die vektorielle Geradenform lautet,  denn dann gilt natürlich auch

y = mx + n  ←

(wobei in der vektoriellen Geradenform oben eine 0 und eine 1 [und zwar in dieser Reihenfolge!] stehen muss)

bzw. konkret

y = 2 x + 3   ←  .

Wir haben aber soeben gesehen, dass dieselbe Gerade g statt durch    auch durch dargestellt werden kann, und dann gibt es leider nicht mehr eine direkte (direkt ablesbare) Umformung in die analytische Geradenform.

Genau genommen kann man der vektoriellen Geradenform nicht mehr direkt m und n für die analytische Geradenform y = mx + n entnehmen, aber immerhin noch halbwegs direkt m

(vgl. oben unsere erste gute Idee

"[...] arg spitzfindig erscheint die Feststellung, dass immerhin

• die Division der beiden Zahlen 8 und 4 aus dem Richtungsvektor der vektoriellen Form
• die Steigung 2 aus der analytischen Form ergibt"):

Schauen wir uns dazu nochmals

an: an den Richtungsvektor lässt sich folgendes Steigungsdreieck zeichnen:

Und damit ergibt sich in der analytischen Form für die Steigung m = = 2.

Wir haben also immerhin schon mal y = 2x + n, kennen aber noch nicht den y-Achsenabschnitt n.

Oder allgemein: wenn die vektorielle Geradenform so

aussieht, ist m =  und haben wir immerhin schon y = x + n, aber noch nicht n .

(Vorsicht: auch hier kann man sich gefährlich vertun, wo c und wo d hinkommt, und deshalb halte ich auch hier die Herleitung für wichtiger als das Auswendiglernen.)

Um jetzt auch noch n zu bestimmen, kehren wir  vorerst zum konkreten Fall zurück:

der Stützvektor endet auf der Geraden g, also liegt der Punkt R ( 1 | 5 ) auf der Geraden g. Das aber heißt, dass seine beiden Koordinaten x = 1 und y = 5 die analytische Geradengleichung y = 2x + n erfüllen müssen, dass also gilt:

5 = 2 • 1 + n ,

und daraus folgt

3 = n

und damit wiederum die analytische Geradenform

y = 2x + 3 .

Und wieder allgemein:

in endet der Stützvektor auf der Geraden g: y = x + n, also liegt der Punkt R ( a | b ) auf der Geraden g. Das aber heißt, dass seine beiden Koordinaten x = a und y = b die analytische Geradengleichung y = x + n erfüllen müssen, dass also gilt:

b = 2 • a + n ,

und daraus folgt

= n

und damit wiederum die analytische Geradenform

y = x + .

(auch das würde ich mir nicht merken, sondern immer kurz herleiten; insgesamt heißt das: ich gehe nie rein algebraisch-rechnerisch vor, sondern halte mich immer an die grafische Darstellung, also an die ANSCHAUUNG;

vgl. oder ). 

---

Bislang haben wir uns nur mit Geraden im Zweidimensionalen befasst. Da stellt sich "natürlich" die Frage, wie's mit

• Geraden im Dreidimensionalen,
• Ebenen  im Dreidimensionalen

steht.

Erstere, also Geraden im Dreidimensionalen, kommen mit

(wie wir noch sehen werden)

gutem Grund in der Überschrift gar nicht vor, und bei letzteren, also Ebenen im Dreidimensionalen, ist in der zweiten Zeile der Überschrift was Merkwürdiges passiert:

 

Links, also bei der analytischen Ebenengleichung, taucht nur ein Fragezeichen auf, weil solche analytischen Ebenengleichungen in der Schule meistens vorher nie durchgenommen wurden

(... wofür es durchaus gute Gründe gibt: analytische Ebenengleichungen sind sehr abstrakt, d.h. ihre Graphen sind schwer vorstellbar; dass sie nun doch eingeführt werden, hat wohl zwei Gründe:

• in Analogie zu  zu den Geraden im Zweidimensionalen, also

y = mx + n  ,

• weil die vektoriellen Ebenengleichungen immerhin halbwegs vorstellbar sind

[wie überhaupt Vieles durch die Vektorgeometrie viel anschaulicher wird, wenn man nur bereit ist, hinzuschauen statt immer nur zu rechnen]).