Potenzgesetze falsch / richtig "beigebracht"

Vorweg: "Potenzgesetze falsch / richtig beigebracht" heißt

• nicht, dass

• falsche Potenzgesetze

(also solche, die den Namen "Gesetz" zu Unrecht tragen)

• oder richtige Potenzgesetze "beigebracht" werden,

• sondern, dass die (richtigen) Potenzgesetze auf

• falsche = ungünstige, irreführende

• oder aber richtige, sachlogische und anschauliche

Art "beigebracht" werden.

Mit den Potenzgesetzen ist es ähnlich wie mit den Bruchrechengesetzen: beide sind

• kein Luxus, mit dem man z.B. einige Rechnungen nur schneller durchführen kann

("es" ginge notfalls aber auch ohne diese Gesetze, wenn auch umständlicher),

• sondern vielmehr dringend nötig, um überhaupt mit Brüchen bzw. Potenzen rechnen zu können,

und sowohl die Bruchrechen- als auch die Potenzgesetze

• vereinfachen Rechnungen enorm bzw.
• machen sie überhaupt erst anschaulich / verständlich.

Z.B. reduzieren die Bruchrechengesetze Bruchrechnungen auf das Rechnen mit natürlichen Zahlen, also die einzigen Rechnungen, die Mathematiker

(die auch nur Dummerchen sind)

überhaupt beherrschen. Ein Beispiel:

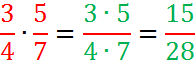
(Nebenbei: auch beim Rechnen mit Dezimalzahlen, die hinterm Komma endlich sind

[also einem möglichen Äquivalent von Brüchen],

wird auf das Rechnen mit natürlichen Zahlen reduziert.

Auch dafür ein Beispiel:

Zur "richtigen" Vermittlung der Potenzgesetze gehört es zu allererst, die Vor- und Nachteile der Potenzen klarzumachen:

1. Die Multiplikation ist eine verkürzte Addition: z.B. ist 5 • 3 eine Abkürzung

• entweder für 5 + 5 + 5

• oder für 3 + 3 + 3 + 3 + 3

(hier sei schon eine später noch wichtige Erkenntnis notiert: Addition und Multiplikation hängen direkt zusammen;

und es sei gleich ohne Erklärung ergänzt, was man auch durch Analogie vermuten könnte: entsprechend hängen Subtraktion und Division zusammen).

2. Das Potenzieren ist eine verkürzte Multiplikation: z.B. ist 5³ eine Abkürzung für 5 • 5 • 5

(hier sei nebenbei festgehalten, dass also das Potenzieren und das Multiplizieren zusammenhängen).

3. Aus a. und b. folgt, dass das Potenzieren eine extrem verkürzte Addition ist.

(Z.B. ist 5³ =   5 • 5                    • 5 =

                   = 5 + 5+ 5 + 5 + 5 + 5 + 5+ 5 + 5 + 5 + 5 + 5+ 5 + 5 + 5 + 5 + 5+ 5 + 5 + 5 + 5 + 5+ 5 + 5 + 5 .)

  Mit Potenzen lassen sich sehr leicht (kurz) riesig große Zahlen aufschreiben. Z.B. ist 2¹⁰ eine Kurzschreibweise

• entweder für 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2, also das Produkt von zehn Zweien, das 1024 ist,
• oder für 2 + 2 + 2 + ... , also die Summe von 512 Zweien, die natürlich auch 1024 ist.

Nun mag man das Ergebnis 1024 noch keineswegs als "riesig groß" empfinden. Gehen wir deshalb mal zu einer wahrhaft gigantisch großen Zahl, nämlich 10⁶⁰, über:

10⁶⁰ bedeutet, dass 10 sechzig mal mit sich selbst malgenommen wird, also

10 • 10 • 10 • ... •10

            sechzig Zehnen,

und das ergibt eine 1 mit sechzig Nullen, also

1 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 =

      = 1.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000

oder wieder hübsch kurz "eine Dezillion".

Hier sieht man sehr deutlich die beiden Extreme: ein und dieselbe Zahl lässt sich

1. sehr kurz

• in Potenzschreibweise als 10⁶⁰, also mit nur vier Ziffern,

• in Worten als "eine Dezillion",

2. sehr lang als

1.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000, also mit 61 Ziffern

schreiben, und daran sieht man sehr gut den Vor- und Nachteil der Potenzschreibweise:

• Vorteil:

die Potenzschreibweise ist

• sehr kurz und damit platzsparend und wenig arbeitsintensiv,

• wenig fehleranfällig

(in der ausgeschriebenen Form 1.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000 vertut man sich doch allzu gern bei der Anzahl der Nullen;

aber das ist letztlich auch egal: die Zahl ist derart gigantisch, dass ein paar Nullen mehr oder weniger an ihrer Unvorstellbarkeit auch nichts mehr ändern;

vgl. das Vermögen von Bill Gates, das sich auf etwa 50.000.000.000 bzw. in Worten 50 Milliarden Dollar beläuft: das ist ein derart unvorstellbar großes [gestohlenes] Vermögen, dass er eine Null mehr oder weniger nichtmal bemerken würde);

der größte Vorteil der Potenzschreibweise, nämlich ihre Kürze, ist aber gleichzeitig auch ihr größter

• Nachteil:

die Potenzschreibweise 10⁶⁰ oder auch der Begriff "eine Dezillion" kommt derart knapp daher, dass man darüber schnell vergisst, dass dahinter die gigantisch große Zahl 1.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000 steckt.

Es muss ein zentrales Anliegen des Mathematikunterrichts sein, die "Explosivität" der Potenzrechnung

(als doppelt abgekürzte Addition)

dennoch halbwegs klar zu machen. Nicht

(was sowieso aussichtslos wäre),

um die Zahl 1.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000 oder auch "nur" Bill Gates Vermögen von 50 Milliarden Dollar zu veranschaulichen, sondern um simple Rechenfehler zu vermeiden, nämlich z.B. den allseits beliebten

10⁶⁰ = 10 • 60,

der entsteht, wenn man denkt:

"der Unterschied, der entsteht, wenn in der Potenzschreibweise die 60

[z.B. durch unsaubere Schreibweise]

ein paar mickrige Millimeter runterrutscht

[wodurch allerdings eigentlich nur die Zahl 1060 entstünde],

kann doch nicht sonderlich bedeutsam sein."

Nun ist aber 10 • 60 nur 600 und damit wahrhaft Welten entfernt von 10⁶⁰ = 1.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.

Denn 10⁶⁰ = 1.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000 ist tatsächlich die ganze Welt bzw. das gesamte Weltall: wenn ich mich recht entsinne, ist 10⁶⁰ = 1.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000 so etwa die geschätzte Anzahl der Atome im gesamten Weltall. Das ist derart viel, dass davor jede Anschauung versagt bzw. man sich davon nur ansatzweise eine Vorstellung machen kann:

• Atome sind derart klitzeklein, dass schon ein Sandkorn aus gigantisch vielen Atomen besteht;
• wie viele Atome mögen dann im Weltall rumschwirren, wenn es schätzungsweise eine Milliarden Milchstraßen gibt

(abgesehen von einigen Vordergrundssternen sind die Lichtpunkte auf diesem Bild
nicht Einzelsterne, sondern ganze Galaxien)

(hier sieht man Ketten [sogenannte Filamente] von Galaxien),

die wiederum jeweils aus etwa einer Milliarden gigantischen Sonnen bestehen?!

Da hilft es auch nicht, zum erheblich "kleineren" Vermögen von Bill Gates überzugehen: 50 Milliarden = 50.000.000.000 = 5•10¹⁰ hat zwar 50 (von 60) Nullen weniger als 10⁶⁰, aber auch da versagt jede Anschauung:

• angenommen, ein Dollarstück ist 1 mm dick,
• wir stapeln Gates' Vermögen in einem Dollarstück-Turm:
• er wäre 50 Milliarden Millimeter = 5 Milliarden Zentimeter = 50 Millionen Meter = 50.000 Kilometer hoch,
  • also etwa 60.000 mal so hoch wie

,

• er würde quergelegt mehr als ein Mal um die Erde reichen
• bzw. etwa ein Sechstel des Weges zum Mond einnehmen:

allesamt Entfernungen, die schier unvorstellbar bleiben!

Die falsche Art, die Potenzgesetze "beizubringen", besteht u.a. darin, sie ohne "Hierarchie" einfach

(und in beliebiger Reihenfolge)

hintereinander zu stellen und dann auswendig lernen zu lassen

(obwohl

[wie so oft in der Mathematik]                                  

das stumpfe Auswendiglernen und, daraus folgend, das automatisierte Anwenden der Potenzgesetze natürlich auch wichtig ist, um sich bei späteren komplexeren Rechnungen, in denen die Potenzgesetze nur noch Beiwerk bzw. Nebenrechnungen sind, nicht noch mit diesen Potenzgesetzen aufhalten zu müssen).

Was ich mit der "Hierarchie" der Potenzgesetze meine, wird deutlicher bei der richtigen Vermittlung der Potenzgesetze: diese sind grob unterteilbar in

1. anschauliche Potenzgesetze,
2. abstrakte Potenzgesetze, die "nur" logisch aus den anschaulichen folgen.

Zu 1., also den anschaulichen Potenzgesetzen:

•  Erstes anschauliches Potenzgesetz: 

                       2³       •            2⁴        =

           =    2 • 2 • 2    •    2 • 2 • 2 • 2 =

              drei Zweien +   vier Zweien =

                        sieben Zweien

          =                     2⁷

Oder kürzer:     2³  • 2⁴ = 2^{(3 + 4)} = 2⁷

Und allgemein: a^m • aⁿ = a^{(m + n)}

(Auch hier wird wieder ein Zusammenhang zwischen Multiplikation und Addition deutlich!)

• Zweites anschauliches Potenzgesetz:

= = = 2³

bzw.                     = 2^{(7 - 4)} = 2³

Und allgemein:

                              = a^{(m - n)}

(... womit

[analog zum Zusammenhang Multiplikation / Addition]

ein Zusammenhang zwischen Division und Subtraktion deutlich wird).

Zeit zum Innehalten, weil da inzwischen so viele interessante und wichtige, aber leicht zu übersehende "Kleinigkeiten" aufgetaucht sind:

die beiden Potenzgesetze a^m • aⁿ = a^{(m + n)} und  = a^{(m - n)} wurden an sehr einfachen Beispielen hergeleitet:

• die Basis war eine besonders einfache natürliche Zahl, nämlich 2

(woran man mal wieder sieht: zum Verständnis reichen ganz simple Beispiele - und sind Taschenrechner überflüssig),

• die Exponenten waren ebenfalls einfache natürliche Zahlen, nämlich 3, 4 und 3 + 4 = 7.

An der Anschaulichkeit der beiden Gesetze ändert sich nichts, wenn man in der Basis anstelle der einfachen natürlichen Zahl 2 eine kompliziertere Zahl, also z.B. , einsetzt oder sogar eine Nicht-Zahl wie z.B. @. Dann ergibt sich nach wie vor anschaulich

                    @³               •                    @⁴ =

          = @  • @ • @        •         @  • @  • @ • @ =

               drei @en          +              vier @en =

                                  sieben @en

         =                        @⁷

Oder kürzer:      @³  • @⁴ = @^{(3 + 4)} = @⁷

Und allgemein: @^m  • @ⁿ = @^{(m + n)}

Alles schön und gut, solange die Exponenten m und n natürliche Zahlen bleiben.

Aber was, wenn die Expontenen nicht mehr natürliche, sondern gebrochene Zahlen sind? Was also soll z.B. • bedeuten? Da sind ja bereits die beiden Einzelteile und unverständlich.

(Bleiben wir nur mal beim ersten Teil . Was soll es bedeuten, die 2 jetzt mal mit sich selbst malzunehmen?

[... aber wohlgemerkt nicht 2 mit , was ja sehr einfach 2 • = 1 ergäbe.]

Bzw. "Was soll es bedeuten ...?" ist [scheint] ja schon falsch gefragt bzw. eine rhetorische Frage, deren mitgelieferte Antwort doch wohl ist: "das kann gar nichts bedeuten, sondern ist schlichtweg Schwachsinn", womit für einen Normalsterblichen das Thema gründlich erledigt wäre.)

Erstaunlich und geradezu typisch für die Mathematik ist aber, dass die beiden Bestandteile und unverständlich sind, man aber wunderbar mit ihnen weiterrechnen kann:

• = = =

... wobei das Ergebnis allerdings wieder unverständlich ist.

Man kann also in der Mathematik wunderbar mit unverstandenen Sachen rumhantieren und sie in neue (oftmals ebenfalls unverstandene) Sachen überführen.

Ein besonders eindrückliches Beispiel, allerdings nicht aus der Potenz-, sondern der Wurzelrechnung

(wobei wir noch sehen werden, dass beide durchaus zusammenhängen):

:

• ich habe keinen blassen Schimmer, was ist

(in dem Sinne, was der halbwegs exakte Dezimalwert von ist),

• ich habe schon gar keinen blassen Schimmer, was ist, aber
• ich kann wunderbar mit und rechnen und
• erhalte in diesem Fall als Ergebnis nicht mal sowas Kompliziertes wie , sondern die umwerfend einfache natürliche Zahl 4.

(Außerhalb der Mathematik ist es genauso: ich kann z.B. Milch und Kaffee problemlos zu Milchkaffee verrühren, ohne im mindesten [chemisch] genau zu wissen, was Milch, Kaffee und. Milchkaffee sind.)

Bislang waren die ersten beiden (anschaulichen) Potenzgesetze für natürliche Exponenten, d.h. Zahlen aus der Menge

₀ = {0, 1, 2, 3, 4 ...} ,

gezeigt worden. Für Mathematiker in ihrem Verallgemeinerungswahn liegt es da nahe, eine erste Zahlbereichserweiterung vorzunehmen, indem sie die Null hinzunehmen:

₀ = {0, 1, 2, 3, 4 ...}

Was aber könnte a⁰ bedeuten? Auf Anhieb scheint das schon wieder falsch gefragt, denn was soll es bedeuten, dass a Null mal mit sich selbst multipliziert wird?

(Vorsicht, Verwechslungsgefahr!: es ist nicht gemeint, dass a mit Null multipliziert wird, wobei sich sehr einfach a • 0 = 0 ergäbe.)

Vermutlich sind viele mathematische Erkenntnisse gar nicht gezielt gesucht worden, sondern haben sie sich zum großen Erstaunen der Entdecker beim Rumhantieren mit Gleichungen ergeben. Im vorliegenden Fall hat also ein Mathematiker vielleicht mal folgendermaßen gerechnet:

... und hat dann über die beiden Enden der Schlange gestaunt:

Mit  a⁰ = 1 haben wir somit das erste nicht anschauliche, sondern abstrakte Potenzgesetz.

(Kleiner Exkurs:

anhand von ist mir erstmals aufgegangen, dass das Gleichheitszeichen nicht kommutativ ist.

Angenommen mal, Arno, Berta und Clara sind gleich groß. Dann gilt doch wohl A = B = C, aber auch jede beliebige andere Reihenfolge, also z.B. auch B = C = A, d.h. man kann A, B und C beliebig austauschen bzw. sie sind bzgl. des Gleichheitszeichens kommutativ.

Statt       

haben aber so einige Schüler in einer Klassenarbeit

geschrieben, und das ist nicht dasselbe:

• in wird auf einem langen Umweg bewiesen, dass 1 = a⁰ ,

• in steht das, was zu beweisen wäre (also a⁰ =1) ganz am Ende, ist also der ganze Anfang nur überflüssige Verzierung unf kann deshalb weggelassen werden. Mit  a⁰ =1 bleibt dann aber nur noch das stehen, was zu beweisen wäre, und somit ist nichts bewiesen.

[Die Version ist ein schönes Beispiel dafür, dass etwas völlig Unverstandenes brav auswendig gelernt wurde.])

Wenn man nun für die Exponenten weitere Zahlbereichserweiterungen vornimmt, also

• erst zu den ganzen (also auch negativen) Zahlen   = { .. -4, -3, -2, -1, 0, 1, 2, 3, 4 .. },
• dann auch noch zu den rationalen Zahlen (Brüchen) ,

so ergeben sich nacheinander folgende Probleme:

1. : z.B. kann man sich auch unter 2 ^-3 wahrhaft nichts anschaulich vorstellen

(es ist einfach nur unsinnig, die 2 nun minus 3 mal mit sich selbst zu multiplizieren),

aber

(man wird inzwischen ahnen, dass das trotzdem möglich ist)

welche Bedeutung können die Mathematiker der  2 ^-3 "hintenrum" dennoch geben?

Ohne zu zeigen, wie genau dieses "hintenrum" aussieht, sei erwähnt:

2 ^-3 = bzw. allgemein a ^-n =  .

Im vorliegenden konkreten Fall ergibt sich damit insgesamt 2 ^-3 = = , und das kann man notfalls in die Dezimalzahl 0,125 umrechnen. 

(Dabei ist an 2 ^-3 = =   zweierlei bemerkenswert:

1. , dass man sich unter   2 ^-3 rein gar nichts, unter      aber sehr wohl etwas vorstellen kann; hier zeigt sich, dass die [gar nicht so] abstrakten Potenzgesetze nicht nur dazu da sind, mit exotischen Exponenten zu rechnen, sondern auch und zu allererst dazu

                    [was allerdings in Schulen viel zu selten Thema, ja Kriterium ist],

           abstrakte Potenzen hintenrum doch noch vorstellbar zu machen;

2. der oben schon angekündigte Zusammenhang zwischen Potenzen und Brüchen!) 

3. : bei der nächsten Zahlbereichserweiterung zu den rationalen Zahlen (Brüchen) hin lassen wir für die Exponenten nun erstmal die "Stammbrüche", also solche mit dem Zähler 1, zu

(Beispiele: ,  , ...).

Wieder ohne genauere Erklärung sei dafür das zugehörige "abstrakte" Potenzgesetz genannt:

(Der einfachste Spezialfall ist da  oder kurz .

Nebenbei: mit haben wir nun auch einen Zusammenhang zwischen Potenz- und Wurzelrechnung!)

Aus und dem in diesem Text nicht hergeleiteten, durchaus anschaulichen Potenzgesetz erhalten wir nun ein (abstraktes) Potenzgesetz für alle Bruch-Exponenten:

Insgesamt ergibt sich damit folgende Systematik der Potenzgesetze:

		Kombination von zwei Potenzen		einzelne Potenzen
		gleiche Basen	gleiche Exponenten
anschauliche Potenzgesetze (anfangs nur für natürliche Exponenten)	Multiplikation	am • an = a(m + n) (Zusammenhang Multiplikation / Addition)	am • bm = (a •b)m (langweiliges Potenzgesetz)
	Division	am : an  = a(m - n) (Zusammenhang Division / Subtraktion)	am : bm = (a :b)m (langweiliges Potenzgesetz)
	Potenz einer Potenz			(Zusammenhang Potenzieren / Multiplikation)
abstrakte Potenzgesetze	für den Exponenten 0			a0 = 1
	für negative ganzzahlige Exponenten			a -n =  (Zusammenhang Potenzen / Bruchrechnung)
	für gebrochene Exponenten			(Zusammenhang Potenzen / Wurzeln)