hoffentlich haben wir ein Problem

vgl. auch Problem- statt Lösungsmathematik

Natürlich kann ich als Laie nicht wirklich kompetent über die Neurobiologie mitreden, aber was ich bislang an neurobiologischen Vorschlägen für das Lernen bzw. den Schulunterricht gelesen und in Vorträgen (etwa von Manfred Spitzer) gehört habe, ist wahrhaft nichts Neues unter der Sonne, sondern wussten schon die "alten" Pädagogen von Pestalozzi bis zur Reformpädagogik usw.

(wodurch es nicht falsch oder weniger dringlich wird).

Sehr schön auf den Punkt gebracht hat das Ulrich Schnabel in "DIE ZEIT 48/2002", indem er am Ende seines Aufsatzes

"Auf der Suche nach dem Kapiertrieb; Hirnforscher beweisen: Erkenntnis macht Erkenntnis macht Lust, Lernen ist sexy. Nur in der Schule ist die Neurodidaktik noch nicht angekommen"

ironisch resümiert:

"Was sich in den Schulen ändern müsste, um den Erkenntnissen der Neurodidakten gerecht zu werden, ist also häufig genau das, was weitsichtige Pädagogen wie etwa Hartmut von Hentig seit Jahrzehnten predigen: den Schülern nicht möglichst viel Stoff eintrichtern wollen, sondern sie zum eigenen Problemlösen anregen [...]

Mit Problemen ist das so ein Problem:

1. Üblicherweise werden Probleme

(wie sich in der Duden-Definition deutlicher bei "problematisch" zeigt)

als negativ angesehen und vermeidet man sie lieber bzw. geht ihnen aus dem Weg.

Für diese negative Sicht gibt es durchaus gute Gründe, denn mit Problemen ist es ähnlich wie mit Fehlern:

"Aus Fehlern und Irrtümern lernen ist für niemanden angenehm [...]" (vgl. "Vom richtigen im Falschen")

Probleme können wehtun und, falls man sie nicht (vollständig?) lösen kann, äußerst frustrierend wirken!

2. Dennoch kann man Probleme aber auch mal als etwas Positives ansehen, nämlich als (am besten selbstgestellte) "Aufgaben" bzw. Herausforderungen

(vgl. in der Duden-Definition etwa "Aufgabe").

Und es mag schwer nach "alten Werten" riechen, aber wenn man eine schwierige Aufgabe dann tatsächlich selbst gelöst hat, ist man natürlich auch besonders stolz!

(... und wenn man bereits mehrfach Probleme gelöst hat, hat man wohl auch eher das Vertrauen, auch das nächste Problem lösen zu können.)

Wichtig an einem "echten" Problem ist aber wohl vor allem, dass ungewiss ist, ob es (vollständig) gelöst werden kann. Und da eben gibt es zwei Arten von Ungewissheit:

1. die Ungewissheit, ob das Problem überhaupt

(nicht unbedingt für mich, aber doch für Fachleute)

lösbar ist

(vgl. etwa Gödels Unvollständigkeitssatz und Turings Weiterführung dieses Satzes),

2. , ob ein prinzipiell lösbares

(von Fachleuten bereits gelöstes)

Problem von mir gelöst werden kann.

Im üblichen Schulunterricht kommen überhaupt nur Aufgaben vor, die in der Mathematikgeschichte längst gelöst wurden. Das hat drei Folgen:

1. muss es den SchülerInneN so erscheinen, als wenn tatsächlich jedes mathematische Problem lösbar, die Mathematik also verdammt rechthaberisch sei;

2. SchülerInneN bleibt eigentlich nur, der Mathematikgeschichte hinterherzuhecheln;

3. da SchülerInnen selbstverständlich nicht alles können, was große MathematikerInnen konnten, wird ihnen permanent das Gefühl vermittelt, dumm zu sein: man misst sich permanent an einem zu großen Vorbild (wird gemessen).

(Letzteres liegt auch daran, dass SchülerInnen eben nur die fertige Mathematikgeschichte, aber nicht ihre oft mühsamen und manchmal auch scheiternden Erkenntniswege kennenlernen.)

Ich meine also, dass durchaus auch exemplarisch unlösbare oder bislang ungelöste mathematische Probleme in den Matheunterricht gehören, also z.B. Apostolos Doxiadis: Onkel Petros und die Goldbachsche Vermutung.

(... womit dann auch vermehrt moderne Mathematik in den Unterricht Einzug halten würde).

Des weiteren muss der Unterrich

(bei in der Tat bereits in der Mathematikgeschichte gelösten Problemen)

von der Einstellung "wir kauen nur nach" wegkommen und (wie?) zu der Einstellung hinführen:

"Wir sind stolz, weil wir selbst [für uns] entdeckt haben, was sogar der große Newton entdeckt hat und was ihn berühmt gemacht hat."

Wichtig oben war vor allem "zum eigenen Problemlösen anregen". Das bedeutet doch zweierlei:

1. die SchülerInnen müssen echte eigene Probleme haben (und als Herausforderung empfinden: "das will ich wissen")

(worunter natürlich nicht zu verstehen ist: "ich habe Probleme, das vorgesetzte mathematische Zeugs zu verstehen und in Mathematik nicht sitzen zu bleiben");

2. die Problemlösung darf ihnen nicht vorgemacht (der Mathematikgeschichte entnommen) werden, sondern sie sollen sie (sicherlich angeleitet und ermutigt) selbst finden.

Mich interessiert hier eher der erste Aspekt, also was ein "echtes" Problem sein und wie es ein "eigenes", also eine selbstgestellte Aufgabe bzw. Herausforderung, werden kann.

Dabei bin ich der festen Überzeugung, dass solch ein echt-eigenes Problem

• weder "jugendnah"

(solche "jugendnahen" Probleme - z.B. Handy-Tarife - sind meistens nur anbiedernd und letztlich Pseudo-Anwendungs-, also eingekleidete Aufgaben, die - und das merken die Jugendlichen sehr schnell - nur dazu dienen, den "Zwangsstoff" zu verpacken)

• noch unbedingt eine "Anwendungsaufgabe" sein muss - aber darf.

Nein, ich glaube felsenfest, dass auch rein innermathematische Probleme "echt-eigen" sein bzw. werden können

(wir möchten eben auch sogenannte "reine" Mathematiker "heranziehen" bzw. ihnen Betätigungsmöglichkeiten liefern!).

Aber fangen wir dennoch mal mit geeigneten (?) Anwendungsaufgaben an.

1. das meiner Erinnerung nach einzige Problem, bei dem ich im "normalen Leben" überhaupt mal gehobene Mathematik gebraucht habe

(ansonsten kann man prächtig ohne jegliche Mathematik durchs Alltagsleben kommen!),

nämlich bei der Anfertigung einer sogenannten "Raumspartreppe" für das Dachgeschoss in unserem Haus:

(hier das fertige Produkt)

Die Raumspartreppe war in Einzelteilen

(Seiten"wangen", Stufen und Schrauben)

sowie vorgebohrt im Baumarkt erhältlich - und passte aus zwei Gründen nicht in unser Dachgeschoss:

1. ist das Geschoss in unserem Haus, in das die Raumspartreppe eingebaut werden sollte, nicht so hoch, wie es bei der vorgefertigten Treppe vorgesehen war;

2. weil vor der Treppe sehr wenig Platz ist, musste für unsere Belange die Raumspartreppe noch "raumspariger" sein, als es bei der vorgefertigten Treppe vorgesehen war.

Unsere Treppe musste also in zweierlei Hinsicht kleiner werden als die vorgefertigte Treppe:

Die Treppe musste daher gekürzt werden und die vorgegebenen Bohrungen waren nicht zu brauchen, sondern es mussten neue vorgenommen werden.

Die Kürzung betraf dabei nicht nur die Seiten"wangen"

(in welchem [veränderten] Winkel mussten sie nun geschnitten werden?),

sondern evtl. auch die Anzahl der Stufen, bei denen einiges zu berücksichtigen war:

1. mussten die Stufen natürlich "gleichverteilt" sein

(durften also nicht z.B. mal 20, mal 30 cm hoch sein),

2. musste (anhand der Originalleiter) beachtet werden, dass eine bequem gehbare Stufenhöhe gewählt wurde, und überlegt werden, wieviel davon höchstens abgewichen werden durfte,

3. musste die oberste Stufe gleichauf mit dem Boden der 3. Etage liegen

(während ganz unten natürlich keine Stufe, sondern der Boden der 2. Etage ist),

4. durften die Stufen sich nicht

(oder nur gering)

zu viel oder zu wenig überlappen: solch eine Raumspartreppe ist wegen der unterschiedlichen Seitenlängen jeder Einzelstufe

sowieso schon sehr schwer zu begehen bzw. sogar gefährlich

(insbesondere, wenn man - noch schlaftrunken - mit dem falschen Fuß anfängt).

Ideal wäre also

während bei

nicht die volle Trittfläche ausgenutzt würde, die Stufen also zu schmal würden, und bei

gefährliche Lücken entstünden.

Typisch an diesem Anwendungsproblem ist, dass es im Gegensatz zu den meisten (schultypischen) Mathematikproblemen vermutlich nicht ideal-eindeutig zu lösen ist, sondern ein Kompromiss zwischen den verschiedenen Anforderungen (u.a. a. - d.) gefunden werden muss

(wobei die Bedingungen a. bis c. allerdings unabdingbar gelten).

Untypisch für eine Schulaufgabe sind auch zwei weitere Punkte: dass

1. die Aufgabe erstmal ganz unmathematisch daherkommt

(wenn natürlich auch durch den Kontext, nämlich Mathe-Unterricht, klar ist, dass alles auf Mathe hinausläuft; aber genau dieser Automatismus, dass also in Mathe wirklich nur Mathe vorkommt, muss ja endlich mal durchbrochen werden; vgl. etwa ),

2. nicht sozusagen "dransteht", welche Mathematik benötigt wird

(wenn auch das Problem natürlich nach Geometrie schreit).

Hier sei nicht en detail nachvollzogen, wie die rechnerische Lösung des Problems aussah, sondern nur, dass dazu

1. der Satz des Pythagoras und

2. mehrfach Trigonometrie

nötig war.

Wo nun könnte, wenn überhaupt, der "Ort" dieser Aufgabe im Mathematikunterricht sein?

1. wohl kaum vor der 9. bzw. 10. Klasse, in der der Satz des Pythagoras sowie die Trigonometrie (durchaus sinnvollerweise) Themen sind;

2. vermutlich wohl auch nicht in der Anfangsphase der Trigonometrie, denn dann müsste man mitten in die Treppenberechnung ellenlange mathematische Exkurse einschieben;

3. sehr gut aber am Ende der Trigonometriephase

(wobei dann allerdings alle - wie im Matheunterricht üblich - wissen, dass garantiert die Trigonometrie angewandt werden muss),

4. in einer späteren "unangekündigten" Wiederholungsphase

(wenn also nicht mehr so eindeutig klar ist, worauf die Aufgabe hinausläuft).

Wirklich streiten kann man sich aber, ob mein damaliges Problem überhaupt zu einem echten Schülerproblem werden kann, denn was interessiert die SchülerInnen meine

(zudem längst fertige)

Treppe?!

(Ich sehe hier sowieso von SchülerInnen ab, die für nichts [Mathematisches] mehr zu interessieren sind).

Ideal wäre es natürlich, wenn die SchülerInnen tatsächlich selbst solch eine (echte!) Treppe bauen sollten/könnten - und warum eigentlich nicht?

Immerhin aber könnte man Modelle bauen

(und in der Tat habe ich damals selbst mit Modellen experimentiert, weil ich auch nicht den vollständigen dreidimensionalen Überblick und überhaupt Angst hatte, meine vielleicht falschen Rechnungen sofort in Holz auszuführen).

2. Das zweite Beispiel erlaube ich mir dem bereits in gelobten Zentralprüfungs-Vorbereitungsheft zu entnehmen:

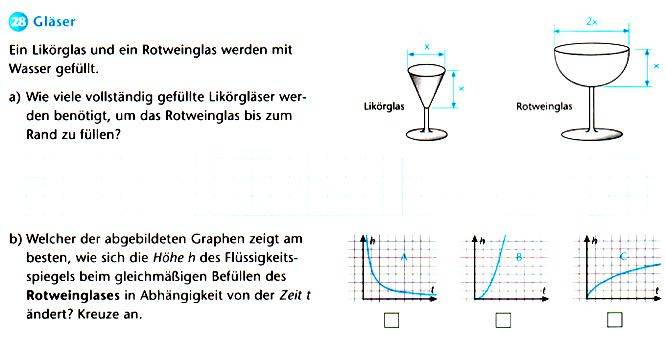
Da sei gleich zu Anfang klargestellt, dass hier keine echte Anwendungsaufgabe vorliegt, denn wann wollte jemals jemand im "Alltagsleben" wissen, wie oft ein Likör- in ein Rotweinglas passt?!

(... oder genauer der Inhalt des einen in das andere)

Kommt hinzu: selbst wenn jemand es wissen wollte, würde er wohl kaum rechnen, also Mathematik benutzen, sondern es einfach durch Umschütten ausprobieren.

Gerade deshalb aber finde ich die Aufgabe so interessant - und erlaube ich mir, sie hier zu zitieren.

Vorerst geht es mir nur um Aufgabenteil a).

Offensichtlich liegt mal wieder Anschauung statt Anwendung vor:

• beim Umfüllproblem sind aus mathematischer Sicht ja sowieso die Gläser (insbesondere die Stiele) uninteressant, sondern hätte man genauso gut

  • statt von einem Likörglas von einem Kegel

  • und statt von einem Rotweinglas von einer Halbkugel

  sprechen können;

• wieso hat man dann dennoch ein Likör(!)- und ein Rotwein(!)glas genommen?: Weil dadurch das Problem viel anschaulicher und fassbarer wird, nämlich sogar derart fassbar, dass man das Umfüllen konkret durchführen kann.

(Auf dieses konkrete Tun wird zurückzukommen sein!)

Anwendungsfern ist die Aufgabe auch dadurch, dass "in freier Wildbahn" Likör- und Rotweingläser wohl kaum gleich hoch und letzteres exakt doppelt so breit wie ersteres ist.

Vollends anwendungsfern wird die Aufgabe aber dadurch, dass nicht konkrete Maße der Gläser vorgegeben werden, sondern immer allgemein mit x gemessen wird.

Da aber leuchtet schon ein entscheidender Tipp hervor - und das eigentlich innermathematisch Interessante: dass nämlich vermutlich die Beziehung der beiden Volumina (von Likör- und Rotweinglas) bei jeder Wahl von x gleich sein wird - was Folgen für mögliche Lösungsansätze hat.

Letztlich interessant an der Aufgabe scheint mir also, das verschiedene Lösungsansätze möglich sind

(und das ist insbesondere in einer Zentralprüfung wichtig, da die SchülerInnen da ja verdammt wenig Zeit haben und somit geradezu mitgeprüft wird, ob die SchülerInnen intelligent-zeitsparende Lösungsansätze finden können).

Anders als bei der Raumspartreppe in 1. ist hier sofort klar, auf welche Mathematik alles hinausläuft, nämlich auf

• die Volumenberechnung eines Kegels,

• die Volumenberechnung einer Halbkugel,

(die entsprechenden Formeln entnehme man unverstanden einer Formelsammlung!)

• und dann die Berechnung des Verhältnisses der beiden Volumina.

(Das soll hier nicht im Einzelnen vorgerechnet werden.)

Mich interessieren hier aber vor allem einfachere, zeitsparende Verfahren:

1. schreit die Aufgabe ja danach, das Umfüllen mal tatsächlich durchzuführen:

• im Unterricht könnte das ja mal mit echten Likör- und Rotweingläsern stattfinden

(aber woher welche mit passenden Maßen nehmen?);

das wäre auch deshalb interessant, weil sich bei verschieden großen x erstaunlicherweise immer dasselbe Verhältnis der Volumina ergäbe und damit die Frage im Raum stünde, warum das so ist;

• aber was schon im Unterricht logistische Schwierigkeiten bereiten würde, wäre in einer Zentralprüfung aus Material- und Zeitgründen schlichtweg ausgeschlossen:

vielmehr müssten die SchülerInnen etwas ganz Entscheidendes beherrschen, nämlich eine "Halbabstraktion" (und auf diese "Halbabstraktion" laufen viele derartige "Anschauungs-statt-Anwendungs-Aufgaben" hinaus, aber gerade diese "Halbabstraktion" macht vielen SchülerInnen enorme Schwierigkeiten; vgl. ): die SchülerInnen müssen in Planskizzen bzw. im Kopf Gläser ineinander umfüllen:

1. in Planskizzen, also eben den in der Aufgabe vorgegebenen:

1. Schritt: .

2. Schritt: , d.h. das Likörglas passt etwa drei Mal nebeneinander in das Rotweinglas hinein.

"nebeneinander" heißt aber, dass alles noch zweidimensional bleibt, und deshalb muss noch die dreidimensionale Erweiterung folgen:

2. im Kopf: nun lässt man in Gedanken (!) noch die äußeren Kegel um den mittleren taumeln, was von oben etwa so aussieht:

Damit lässt sich zweifelsohne kein genauer Wert ermitteln, aber immerhin ahnt man, dass dreidimensional noch einige Likörgläser mehr in das Rotweinglas passen als in der zweidimensionalen Version . Sagen wir also mal - über den Daumen gepeilt - doppelt so viele, so dass insgesamt schätzungsweise 6 Likörgläser in das Rotweinglas passen.

Nochmals: in einer Prüfung ginge es sicherlich um den (annähernd?) exakten Wert, würde 6 also

(falls wir nicht zufällig das exakte Ergebnis getroffen haben)

wohl als falsch gelten.

Aber immerhin haben wir mit 6 eine ungefähre Vorstellung von der Größenordnung - und können unser Rechenergebnis daran messen (ob uns also evtl. ein Rechenfehler unterlaufen ist).

2. bleibt uns also eine Rechnung wohl doch nicht erspart. Damit aber kommen wir auf den oben bereits genannten Tipp zurück, dass bei verschiedenen x vermutlich doch immer dasselbe Verhältnis herauskommt.

Dann aber reicht es

(da ja nicht nach dem Rechenweg, sondern nur nach dem Ergebnis gefragt ist),

die Berechnung der Volumina und ihres Verhältnisses für einen besonders einfachen Wert, nämlich x = 1, durchzuführen

(vgl. ),

 was die Rechnung doch erheblich vereinfacht und beschleunigt.

Hier sei zuguterletzt doch das Ergebnis verraten: das Verhältnis von Likör- zu Rotweinglas ist immer (unabhängig von x) 1 : 8, und die Unabhängigkeit von x liegt daran, dass es sich bei der Verhältnisbestimmung rauskürzt.

Ich wette aber, dass die Aufgabe überhaupt nur gestellt wurde, weil das Ergebnis so auf Anhieb erstaunlich ist:

• die Unabhängigkeit von x

• das so einfache und "glatte" Verhältnis 1 : 8.

Damit aber noch kurz zum Aufgabenteil b):

• auch da wird man sukzessive im Kopf Wasser (?) zugießen müssen, und zwar pro Zeiteinheit immer dieselbe Menge;

• und auch da wird man eine "selbsterlebte" Situation ergänzen müssen, die sogar noch aufschlussreicher ist, wenn man ein Glas nimmt, das sich nach oben verjüngt: wohl jeder (?) hat mal bei solch einem Glas oder solch einer Blumenvase die Erfahrung gemacht, dass der Flüssigkeitsspiegel anfangs ziemlich langsam steigt, am Ende aber so rasend schnell, dass das Glas bzw. die Vase überläuft.

Also wird es bei einem unten schmalen und oben breiten Glas umgekehrt sein!

(Eine wahrhaft entscheidende Frage ist dabei, ob wirklich jedeR [SchülerIn] solche Vorerfahrungen mitbringt. Immerhin habe ich beispielsweise auf Klassenfahrten schon SchülerInnen erlebt, die beispielsweise noch nie einen Esstisch abgeräumt und gesäubert oder noch nie Bettwäsche aufgezogen hatten und das dann folgerichtig auch wirklich nicht konnten.
Oder in einer Klausur wusste eine Schülerin wirklich nicht, wie ein 11-Meter im Fussball funktioniert [vom 11-Meter-Punkt aus] und hatte daher keine Chance, ihr durchaus vorhandenes mathematisches Wissen anhand einer entsprechenden "Anwendungs"-Aufgabe zu beweisen.)

Schön finde ich solche Aufgaben wie b) vor allem deshalb, weil da endlich mal eine Vorstellung von Funktionsgraphen entwickelt wird.