Produkt- und Kettenregel
![]()
Vorweg:
in vielen Schüleraugen sehen
die unten behandelte Funktion f: y = (x2-6x+8)•e2x-3
und erst recht ihre Ableitung f ': y = (2x - 6) • e2x-3 + (x2- 6x+ 8) • e 2x - 3 • 2
wohl abschreckend monströs
 aus
aus
("da brauche ich erst gar nicht anzufangen, denn das kann ich sowieso nicht").
Aber ich nehme die Funktion f: y = (x2-6x+8)•e2x-3 hier nur, weil genau solche Aufgaben nunmal häufig im üblichen Unterricht auftauchen - und frage hier nicht, ob das inner- oder außermathematisch sinnvoll ist.
Benötigtes Vorwissen:
 und
h
und
h


zusammensetzen kann,
Nun gibt es aber noch drei andere Möglichkeiten, zwei Funktionen g und h zu einer Funktion f zusammenzusetzen:
(s.u. die "Produktregel"),
(s.u. die "Quotientenregel"),
(zu diesem wohl schwierigsten Fall s.u. die "Kettenregel"; dort wird auch erklärt, was eine "Verkettung" überhaupt ist).
Zwei Bemerkungen vorweg:
| A. |
Die Produkt- wie auch die Kettenregel sind nur dann nötig, wenn eine Funktion f aus zwei verschiedenartigen Funktionen g und h (im Folgenden jeweils einer ganzrationalen und einer Exponentialfunktion) zusammengesetzt ist. |
| B. |
Sowohl die Produkt- als auch die Kettenregel ermöglichen es,
|
Die Produktregel
Ein Produkt liegt vor, wenn
Bevor man überhaupt mit einer Ableitungsregel und dem Rechnen loslegt, sollte
man also mit Argusaugen darauf achten, ob ein
![]() auftaucht:
auftaucht:
In einer Schulbuch-Aufgabe taucht der Funktionsterm (x2-6x+8)•e2x-3 auf
(zugehöriger Funktionsgraph:
 ;
es ist unbedingt ratsam, sich vor allen Rechnungen den
Funktionsgraphen am Computer anzusehen, denn dann weiß man immerhin, dass
man mit den Rechnungen links ein Maximum und rechts
ein Minimum erhalten muss - und was falsch
gemacht hat, wenn man was anderes rausbekommt; falls letzteres der Fall
ist und ich keine Zeit mehr habe, den Fehler zu korrigieren, würde ich als
Schüler immerhin erwähnen, dass mir der Fehler aufgefallen ist
- und als Lehrer würde ich für diese Erkenntnis Punkte
vergeben).
;
es ist unbedingt ratsam, sich vor allen Rechnungen den
Funktionsgraphen am Computer anzusehen, denn dann weiß man immerhin, dass
man mit den Rechnungen links ein Maximum und rechts
ein Minimum erhalten muss - und was falsch
gemacht hat, wenn man was anderes rausbekommt; falls letzteres der Fall
ist und ich keine Zeit mehr habe, den Fehler zu korrigieren, würde ich als
Schüler immerhin erwähnen, dass mir der Fehler aufgefallen ist
- und als Lehrer würde ich für diese Erkenntnis Punkte
vergeben).
Der Funktionsterm (x2-6x+8)•e2x-3 sieht erstmal katastrophal schwierig (und wahnsinnig intelligent) aus
 ,
,
und in der Tat haben die Schulbuchautoren da sämtliche Schwierigkeiten aus der Unterrichtseinheit „Produkt- und Kettenregel“ reingepackt. Man könnte also vermuten, dass die Konfusion der Schüler da geradezu Absicht war.
Aber da lässt sich dennoch Ordnung reinbringen bzw. erkennen
grob hingeschaut, ist erstmal nur das Malzeichen wichtig:
(x2-6x+8)![]() e2x-3
e2x-3
bzw. noch gröber
![]()
![]()
![]()
und am gröbsten
![]()
![]()
![]() .
.
(Nebenbei: wir haben im scheinbaren Chaos inzwischen also eine sehr einfache Ordnung gefunden: da werden zwei Sachen miteinander multipliziert, und das ist doch nun wahrhaft nicht neu.)
Bei
![]()
![]()
![]() ist es vorerst herzhaft egal, was in
ist es vorerst herzhaft egal, was in
![]() und was in
und was in
![]() steht
steht
Wichtig ist hier einzig und allein, dass
(das Blinken des Malpunkts lasse ich ab jetzt aber weg, weil es auf die Dauer doch nervig ist und von neuen Erkenntnissen ablenkt),
also ein Produkt vorliegt
(die hier nicht hergeleitet wird):
| Produktregel: | f (x) =
f (x) = f (x) = |
In unserem Beispiel (x2-6x+8) • e2x-3 ist
f (x) = (x2-6x+8) • e2x-3 ⇒ f ' (x) = (2x - 6) • e2x-3 + (x2-6x+8) • (e2x-3 )'
... was den kleinen Schönheitsfehler hat, dass wir die Ableitung (e2x-3 )' noch nicht berechnen können (s.u. bei der "Kettenregel").
Deshalb sei das Beispiel erstmal vereinfacht, indem wir statt h (x) = (e2x-3 ) nun die Variante h (x) = ex nehmen
(wobei daran erinnert sei, dass die Ableitung von ex wunderbar einfach wieder ex ist).
 ,
,f (x) = (x2-6x+8) • ex ⇒ f ' (x) = (2x - 6) • ex + (x2-6x+8) • ex
Wichtig an der Produktregel
f (x) = g(x) • h(x) ⇒ f '(x) = g'(x) • h(x) + g(x) • h'(x)
ist, dass wir damit
die Ableitung der zusammengesetzten Funktion f (x)
auf die bereits bekannten Teilfunktionen g und h und deren Ableitungen g ' und h ' zurückführen können.
Schauen wir uns aber das Ergebnis f '(x) = (2x - 6) • ex + (x2-6x+8) • ex nochmals genauer an:
da fällt auf, dass ex in beiden Summanden auftaucht, weshalb wir ex mit dem Distributivgesetz ausklammern können:
f '(x) = (2x - 6) • ex + (x2-6x+ 8) • ex =
= [ (2x - 6) + (x2-6x+ 8) ] • ex =
= [ 2x - 6 + x2-6x+ 8 ] • ex =
= [ x2-4x+ 2 ] • ex
Oder kurz f '(x) = [ x2-4x +2 ] • ex .
Daran ist zweierlei bemerkenswert:
: die Funktion h(x)
=
ex
taucht in der Ableitung (und allen
weiteren Ableitungen) exakt genauso wieder auf wie in der Ausgangsfunktion
f.
![]()
Im vorliegenden Fall muss also
[x2-4x+2]
![]() ex =
0 sein.
ex =
0 sein.
Hier aber kommt ein enorm wichtiger "Trick" zum Tragen: das Produkt zweier Zahlen ist 0 , wenn
a
![]() b =
0
⇔
a
= 0 oder
b
= 0
b =
0
⇔
a
= 0 oder
b
= 0
![]()
![]()
![]() =
0
⇔
=
0
⇔![]() = 0 oder
= 0 oder ![]() = 0
= 0
In unserem Beispiel:
![]()
![]()
![]() =
0
⇔
=
0
⇔![]() = 0 oder
= 0 oder
![]() =
0
=
0
(... wobei ich hier das Wort "oder" plötzlich nicht mehr im umgangssprachlichen, sondern im mathematischen Sinn verwende).
Fangen wir hinten mit
![]() =
0 an: bekanntermaßen (?) haben
Exponentialfunktionen keine Nullstellen N ( ? |
0 )
=
0 an: bekanntermaßen (?) haben
Exponentialfunktionen keine Nullstellen N ( ? |
0 )
(sondern liegen komplett oberhalb der x-Achse).
Es ist also ausgeschlossen, dass
![]() =
0 ist, weshalb wir diesen Fall
streichen können:
=
0 ist, weshalb wir diesen Fall
streichen können:
![]()
Somit bleibt nur der Fall
![]() =
0 , also eine altbekannte
quadratische Gleichung, die wir mit der pq-Formel
=
0 , also eine altbekannte
quadratische Gleichung, die wir mit der pq-Formel
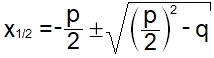 lösen können, wobei
x1 = 2 +
lösen können, wobei
x1 = 2 + ![]() ≈
3,5 und x2 = 2 -
≈
3,5 und x2 = 2 -
![]() ≈ 0,5
herauskommen. Als
≈ 0,5
herauskommen. Als
(Wir sparen uns hier mal
Zur Kettenregel
Schauen wir uns nochmals die Funktion f: y =
![]()
![]()
![]() vom Anfang an, an der wir die Notwendigkeit einer
Produktregel hergeleitet hatten, mit der wir f
nun immerhin schon mal halbwegs ableiten
können:
vom Anfang an, an der wir die Notwendigkeit einer
Produktregel hergeleitet hatten, mit der wir f
nun immerhin schon mal halbwegs ableiten
können:
f '(x) =. g'(x) • h(x) + g(x) • h'(x)
f '(x) = (2x + 6) • e2x-3 + (x2+6x+8) • (e2x-3)'
Nur "halbwegs ableiten", weil noch immer nicht geklärt ist, wie man (e2x-3)' berechnet, also (e2x-3) ableitet.
Wir wissen allerdings bereits, dass die Ableitung von ex idiotensicher einfach wieder ex ist. Was also ist bei e2x-3 komplizierter geworden?
Um das herauszufinden, benutzen wir erstmal andere Farben, nämlich
so dass sich insgesamt
![]() ergibt.
ergibt.
Nun setzen wir in
![]() für x eine beliebige Zahl ein, also z.B.
4. Dann müssen wir rechnen:
für x eine beliebige Zahl ein, also z.B.
4. Dann müssen wir rechnen:

Dabei soll uns der Dezimalwert 148,4131 nicht weiter interessieren, zumal er ja nur ungenau ist. Sondern uns interessiert nur der Rechenweg, also

Wenn man sich Funktionen als Maschinen vorstellt, die jedes vorne eingegebene x nach derselben Regel verarbeiten,
(h arbeitet also nicht völlig unabhängig von g).
Die Teilmaschine h
 ,
,
 ins Westfalen-Stadion
ins Westfalen-Stadion
 .
.



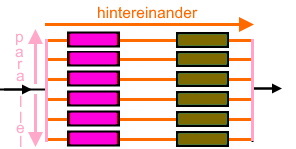
Schauen wir uns im Vergleich mit der "Hintereinander-Schaltung" von g und h in

nun mal eine "Parallelschaltung" von g und h an:
allgemein:

für x = 4 :

Hier wird
Allerdings kommen dadurch rechts aus unserer Maschine ZWEI Ergebnisse heraus, nämlich

Weil da aber einem x (bzw. 4 ) MEHRERE Ergebnisse zugeordnete werden, liegt hier KEINE Funktion vor.
Nebenbei: eine „Parallelschaltung“ von Waschen und Bügeln ist gar nicht möglich, da man ein (!) Hemd nicht gleichzeitig waschen UND bügeln kann.
Nur so viel zum „Parallelschalten“ von Funktionen, damit man das auch mal gesehen hat - und dadurch vielleicht doch das „Hintereinanderschalten“ von Funktionen besser versteht.
(jetzt wieder hintereinander geschalteten)
Teilmaschinen etwas anderes herauskommt:



![]()
|
Eine Funktion f ,
nennt man „verkettet“ |
(„verkettet“ wohl wegen der
Abhängigkeit der beiden Teilfunktionen g
und h voneinander:
![]()
eine fürchterliche Version von „verkettet“ ist nebenbei
die
![]() „chain gang“
„chain gang“
 ).
).
Genau genommen ist
nicht g von h abhängig,
sondern nur umgekehrt h von g, da h ja das Ergebnis von g weiter verarbeitet.
Man könnte auch sagen:

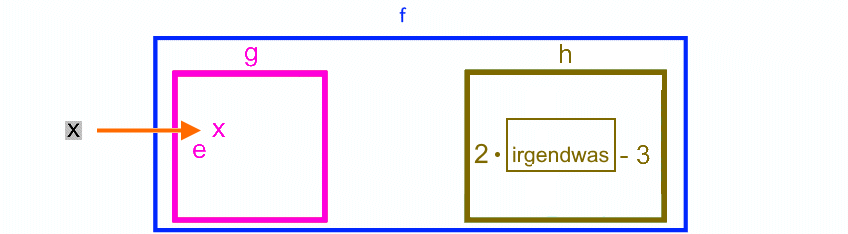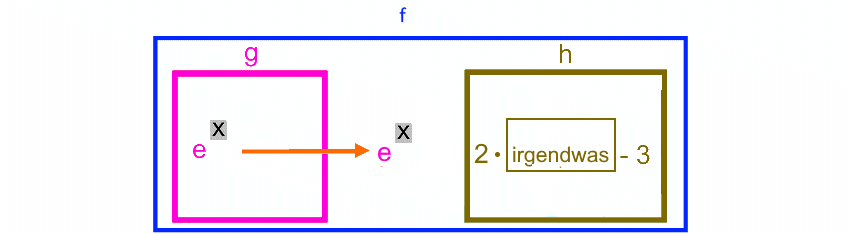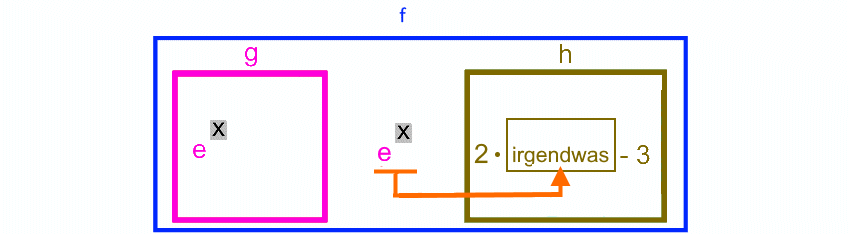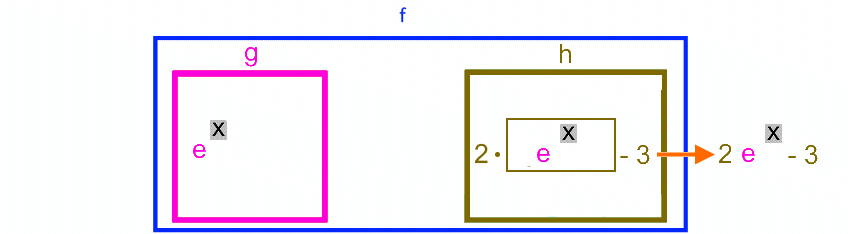
Da die Verkettung von Funktionen Schülern erfahrungsgemäß einige Schwierigkeiten bereitet, hier noch ein besonders einfaches Beispiel:
die Funktion f besteht aus den beiden Teilfunktionen
 .
.
Wenn nun h das Ergebnis
von g
weiterverarbeiten soll, erhalten wir also
 .
.
(Ein Beispiel: irgendwas = 4 . Dann ist
 =
=
 =
=
 =
12 2
= 144 .)
=
12 2
= 144 .)
Oder mathematischer gesagt:
 .
.
Wenn nun h das Ergebnis
von g
weiterverarbeiten soll, erhalten wir also

bzw. (3 • x ) 2 .
|
Und das schreibt man auch h (g ( x ) ). Weil da g innerhalb der großen Klammer ( ) steht, nennt man g die "innere Funktion". Und weil h außerhalb der großen Klammer ( ) steht, nennt man h die "äußere Funktion". Dabei ist
|
Um zu verstehen, wie man die innere Funktion g und die äußere Funktion h findet (und beide auseinanderhält), schauen wir uns nochmals die beiden bereits oben benutzten Funktionsterme
an.
Da die beiden Funktionsterme so verwirrend, ja gefährlich ähnlich aussehen
(außer dass die 2 offensichtlich
seien die Exponenten mal viel deutlicher hochgestellt , und außerdem seien Malpunkte ergänzt.
(Nebenbei ein kleiner Tipp: damit einem die Exponenten einer unteren Zeile nicht versehentlich in eine obere Zeile rutschen, schreibe man mit doppeltem Zeilenabstand, sobald überhaupt Exponenten vorkommen.
Und sowieso schreibe man die Exponenten deutlich höher als die Basen, da die Exponenten sonst allzu schnell in die Basen herabrutschen, was garantiert zu Fehlern führt.)
In viel deutlicherer Schreibweise erhalten wir also:

Wenn man nun herausfinden möchte, was jeweils die innere Funktion g und was die äußere Funktion h ist, ist es ratsam, für x mal eine konkrete Zahl einzusetzen, also z.B. x = 4 .
Wir erhalten dann
Angenommen mal, wir wollten diese Terme nun vereinfachen bzw. ausrechnen:
(also
![]() ≈
2,7182
≈
2,7182![]() ≈
54,5981)
≈
54,5981)
und das Ergebnis dieser Rechnung
(also 2 • x - 3 ≈ 2 • 54,5981 - 3 ≈ 109,1963 - 3 = 106,1963);
somit ist hier

(also 2 • 4 - 3 = 8 - 3 = 5)
und das Ergebnis dieser Rechnung
(also e
![]() ≈ 2,7182
≈ 2,7182
![]() ≈
148,4131);
≈
148,4131);
somit ist hier

Damit aber endlich zur eigentlichen "Kettennregel":
(wobei
zu einer Funktion f verkettet (s.o.) sind,
f ' = h ' (g) • g '
Oder kurz:
| Kettenregel: f = h (g) ⇒ f ' = h ' (g) • g ' |
Diese Kettenregel soll hier
(wie oben die Produktregel)
nicht hergeleitet / bewiesen, wohl aber auf konkrete Funktionen angewandt werden, und zwar wieder auf die beiden oben schon mehrfach behandelten Funktionen
Zu f: y = 2 e x - 3 :
Wie oben bereits gezeigt, ist hier

Da wir in der Kettenregel g ' und h ' brauchen, ist es ratsam, diese schon mal vorweg auszurechnen:
Mit der Kettenregel
f ' = h ' (g ) • g '
folgt
f '(x) = h ' (g(x)) • g '(x)
= 2 • e x
Oder kurz:
f (x) = 2 e x - 3
⇒
f
' (x) = 2
e x
![]()
Zu f: y = e 2x - 3 :
Wie oben bereits gezeigt, ist hier

Vorweg berechnen wir schon mal g ' und h ':
Mit der Kettenregel
f ' = h ' (g ) • g '
folgt
f ' (x) = h ' ( g(x) ) • g ' (x)
= ![]()
Oder kurz:
f (x) = e 2x - 3
⇒ f
' (x) = e 2x - 3 •
2
![]()
Zu Anfang dieses Textes hatten wir uns die Frage gestellt, wie man die verschachtelte Funktion f: y = (x2-6x+8) • e2x-3 ableiten könnte.
Weil da ein ![]() auftauchte, hatten wir mit der
Produktregel
immerhin schon berechnen können
auftauchte, hatten wir mit der
Produktregel
immerhin schon berechnen können
f : y = (x2-6x+8) • e2x-3 ⇒ f ': y = (2x - 6) • e2x-3 + (x2-6x+8) • (e2x-3 )',
wobei uns da allerdings noch nicht klar war, wie wir die Ableitung (e2x-3 )' bestimmen könnten.
Inzwischen wissen wir aber: (e2x-3 )' = e 2x - 3 • 2 , und wenn wir deshalb (e2x-3 )' durch e 2x - 3 • 2 ersetzen, erhalten wir
f ' : y = (2x - 6) • e2x-3 + (x2-6x+8) • (e2x-3 )' ,
f ': y = (2x - 6) • e2x-3 + (x2-6x+8) • e 2x - 3 • 2
(... was erstmal scheußlich unübersichtlich aussieht; um es aber zu vereinfachen, bedarf es absoluter Genauigkeit und der routinierten Anwendung von Rechengesetzen).
Da taucht e 2x - 3 in beiden Summanden auf, weshalb wir es mit dem Distributivgesetz ausklammern können:
f ' : y = (2x - 6) • e2x-3 + (x2- 6x+ 8) • e 2x - 3 • 2 =
= ( (2x - 6) + (x2- 6x+ 8) • 2 ) • e 2x - 3 =
= ( 2x - 6 + 2x2-12x+16 ) • e 2x - 3 =
= ( 2x2-10x+10 ) • e 2x - 3
oder kurz
f : y = (x2-6x+8) • e 2x - 3
⇒ f ': y
=
(2x2-10x+10)
•
e
2x - 3
![]()
Bei Kurvendiskussionen brauchen wir f ' , um die notwendige Bedingung f ' (x) = 0 für Minima / Maxima / Sattelpunkte zu überprüfen, im vorliegenden Fall also
(2x2-10x+10) • e 2x - 3 = 0
Hier greifen wir wieder zu dem bereits oben benutzten Trick:
a
![]() b =
0
⇔
a
= 0 oder
b
= 0
b =
0
⇔
a
= 0 oder
b
= 0
![]()
![]()
![]() =
0
⇔
=
0
⇔![]() = 0 oder
= 0 oder
![]() = 0
= 0
Im vorliegenden Fall:
![]()
![]()
![]() =
0
⇔
=
0
⇔![]() = 0 oder
= 0 oder
![]() =
0
=
0
![]()
![]()
![]() =
0
⇔
=
0
⇔![]() = 0 oder
= 0 oder
![]()
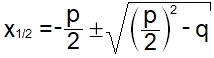 lösen, wobei
x1 = 2,5 +
lösen, wobei
x1 = 2,5 + Last but not least ...
... eine enorme Vereinfachung: wir
verallgemeinern
![]() ,
,
![]() ,
,
![]() und
und
![]() ohne Beweis:
ohne Beweis:
|
Exponentialfunktionsterme bleiben beim Ableiten immer unverändert erhalten. |
Ein Beispiel:

Dabei ist
Wir sparen uns aber die schwierige Bestimmung von h '
und setzen in der Kettenregel
für h
'
(g(x))
tolldreist einfach wieder
![]() aus f ein:
aus f ein:
f ' : y = h ' (g(x)) • g ' (x) =
= ![]() •
g
'
(x)
=
•
g
'
(x)
=
=
![]() •
2x
•
2x
bzw. kurz
f
' :
y =
![]() •
2x
.
•
2x
.
Und weil derselbe Exponentialterm in der Ausgangsfunktion f und in der Ableitung f ' auftaucht, kann man ihn oftmals mit dem Distributivgesetz aus der Ableitung ausklammern und braucht dann nur noch den Rest (oftmals eine ganzrationale Funktion) zu betrachten (s.o.).