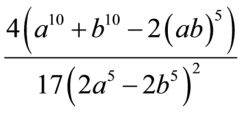 ist pseudoschwierig
ist pseudoschwierig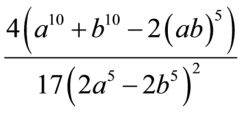 ist pseudoschwierig
ist pseudoschwierig
| Vgl. auch |
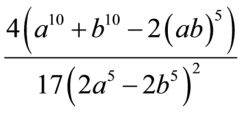 ist eine jener Aufgaben, wie sie beim Thema Termumformungen bzw. Potenzen seitenweise in klassischen Schulbüchern auftauchen.
ist eine jener Aufgaben, wie sie beim Thema Termumformungen bzw. Potenzen seitenweise in klassischen Schulbüchern auftauchen.
Mir scheint, vor nichts außer Textaufgaben haben SchülerInnen solch eine Angst wie vor solchen Term-Monstern.
Diese gigantischen Terme riechen doch schwer danach, dass da die Schulbuchautoren alle nur denkbaren Schwierigkeiten eingebaut haben, damit die SchülerInnen auch unbedingt an mindestens einer Ecke scheitern - und somit auch das Gesamtergebnis falsch ist.
(Nebenbei: die übliche Aufforderung ist da "vereinfache!", was allerdings doppelt problematisch ist:
wird das "bestmögliche" Ergebnis oftmals von SchülerInneN gar nicht als einfach empfunden, haben sie also kein Ziel vor Augen;
"erleben" sie nie die Einfachheit, wenn sie sich auch nur einmal verrechnen.
Und vielleicht empfinden die SchülerInnen sogar die [wie im vorliegenden Fall] Einfachheit am Ende nicht als wunderschöne Auflösung aller Probleme, sondern nur als Schikane: "Warum verkompliziert man es erst dermaßen, damit wir es wieder mühsamst [nicht] aufdröseln?!"
Überhaupt kann man es gar nicht deutlich genug herausstellen: in der Mathematik gibt es völlig unterschiedlich aussehende [fallweise nützliche] Schreibweisen für ein und denselben Sachverhalt.)
Man muss sich wirklich mal
(im Nachhinein, wenn man also schon "richtiger" Mathematiker ist, höchst mühsam)
klar machen, welche Fülle an Schwierigkeiten in 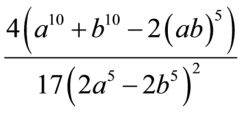 steckt:
steckt:
ein Bruch samt Bruchrechen-/Kürzungsregeln,
die zweite binomische Formel (die zudem im Nenner noch "verdreht" ist),
Potenzen samt Potenzgesetzen
(der eigentliche Anlass, um diese Aufgabe durchzunehmen),
Klammerauflösen
(mit der geradezu paradoxen Schwierigkeit, dass im Nenner, wenn (2a5-2b5)2 mittels "Binomi" aufgelöst wird, zwischenzeitlich eine neue Klammer eingefügt werden muss, und zwar wegen des ...),
Assoziativgesetz(es)
... und einiges davon mehrfach.
Und da muss nun einE SchülerIn nur an einer einzigen Stelle eine Schwierigkeit (eine Lücke aus Vorjahren) haben, und schon geht alles den Bach runter!
Die Fülle der Einzelprobleme ist derart groß, dass in einer durchaus durchschnittlichen Klasse überhaupt nur eine einzige Schülerin das richtige Ergebnis erhalten hat!
Dabei muss man natürlich unterscheiden:
: Haben sich SchülerInnen nur verrechnet
(was mir ja auch andauernd passiert!),
ansonsten aber alle grundlegenden Verfahren verstanden bzw. parat gehabt?
: Oder scheitert´s bei ihnen an der Unkenntnis, dem Nichterkennen oder der falschen Ausführung eines dieser grundlegenden Verfahren?
: Oder haben sie einfach vor lauter Schwierigkeiten die Übersicht verloren, ja wussten nichtmal, wo anfangen ("ich versteh´ das ALLES nicht").
Da kann ich SchülerInnen nur zweierlei empfehlen:
, sich die Einzelprobleme deutlich klar zu machen
(d.h. auch sich deutlich einzugestehen, was sie nicht können),
d.h. das Gesamtproblem zu zergliedern, und dann
, die Einzelprobleme nacheinander (statt mehrere gleichzeitig) abzuarbeiten.
Es ist - zumindest auf den ersten Blick - allemal erstaunlich, dass sich der höchst umständliche Ausdruck 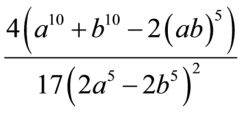 zum simplen
zum simplen ![]() vereinfachen lässt (mit ihm identisch ist), also
vereinfachen lässt (mit ihm identisch ist), also
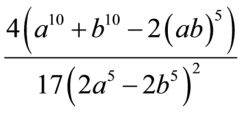 =
= ![]()
Und ich gestehe gerne ein, dass ich das auch nicht auf Anhieb gesehen, sondern erstmal umständlich und in vielen Schritten rechnen musste, um dann am Ende ![]() zu erhalten.
zu erhalten.
Im selben Augenblick aber, in dem ich dieses ![]() hatte, fiel es mir wie Schuppen von den Augen - und habe ich mich fast ein wenig geschämt, dass ich das nicht sofort gesehen hatte.
hatte, fiel es mir wie Schuppen von den Augen - und habe ich mich fast ein wenig geschämt, dass ich das nicht sofort gesehen hatte.
Kleiner Einschub:
so erstaunlich ist es nun auch wieder nicht, dass sich 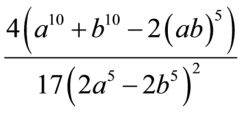 zum simplen
zum simplen ![]() vereinfachen lässt:
vereinfachen lässt:
sorgen Schulbuchautoren ja allzu gerne dafür, dass ein (überraschend) einfaches Ergebnis herauskommt, damit die Anweisung "vereinfache!" auch wirklich einen sinn macht;
weiß ich ja längst (und sollten SchülerInnen sehr viel mehr wissen), dass Schulbuchautoren
nicht mit vielen komplizierten Termen anfangen und dann solange rechnen, bis endlich mal ein sehr einfacher herauskommt,
sondern dass sie umgekehrt vorgehen, nämlich vom gewünschten einfachen Ergebnis ausgehen es dann verkomplizieren und dann diese Verkomplizierung den SchülerInneN geben, auf dass diese wieder zum Einfachen zurückrechnen
(auch das hat was Frustrierendes: ich soll vereinfachen, was schon mal einfach war).
Angenommen also mal, man hat (wie ich) sehr lange umständlich gerechnet und merkt erst ganz am Ende
(wenn man überhaupt richtig gerechnet hat und alle "Grundverfahren" parat hatte),
dass ![]() herauskommt. Dann sollte man es nicht einfach bei diesem Ergebnis belassen, sondern (wie ich umgehend) sich fragen, wieso es denn zustande kam.
herauskommt. Dann sollte man es nicht einfach bei diesem Ergebnis belassen, sondern (wie ich umgehend) sich fragen, wieso es denn zustande kam.
Und da habe ich dann sofort erkannt, dass sich zwei Dinge gegenseitig "aufheben" bzw. kürzen lassen, weil sie (wenn auch versteckt) identisch sind:
(Solch ein Vergleich gelingt einem [?] sofort, wenn man
einen Zahlenvergleich anstellt [4/2, 5/10]
und erkennt, dass im Zähler und Nenner fast derselbe "Binomi" [wenn auch in verschiedenen Formen] steht
(und genau das haben natürlich die Schulbuchautoren gewusst und deshalb auch von Anfang an, dass
"herauskommt").
Es scheint mir also ein sinnvolles pädagogisches Rezept, ja fast ein "Muss" zu sein,
, wenn man nach langem Rechnen ein einfaches Ergebnis erhält, dieses nicht nur hinzunehmen und prompt zur nächsten Aufgabe überzugehen, sondern sich zu fragen, weshalb es so einfach geraten ist,
, sich auch mal die langwierigen Rechnungen völlig zu sparen und gleich (etwa anhand eines Lehrer-Lösungshefts) mit
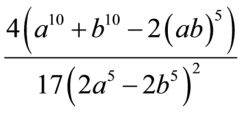 =
= ![]()
anzufangen und sich dann die Frage aus 1. zu stellen
(und wenn man bereits das Ergebnis kennt, wäre es ja nur Schikane, nochmals umständlich auf es hinrechnen zu sollen).
Keine Ahnung, was die Schulbuchautoren mit 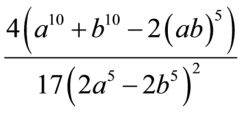 bezweckt haben:
bezweckt haben:
das umständliche "Ausrechnen" und/oder
die Schulung des "strukturierenden Blicks" wie in 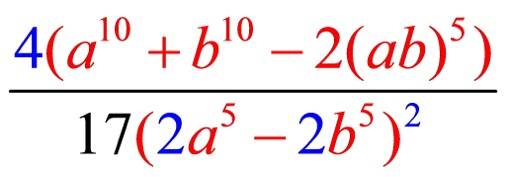 ? War es also ihre Absicht, dass man ihnen (der Konstruktion der Aufgabe) auf die Schliche kommt?
? War es also ihre Absicht, dass man ihnen (der Konstruktion der Aufgabe) auf die Schliche kommt?
Ein Parallelbeispiel aus der Kombinatorik:
in einem Schulbuch stehen nacheinander die beiden folgenden (Teil-)Aufgaben:

Die Gesamtaufgabe 11 erzeugt einen schizophrenen Eindruck:
zwar ist die Anfangskonstellation "3 Mädchen, 2 Jungen" in a) und b) identisch, aber
auf den ersten Blick scheinen die Probleme a) und b) doch völlig unterschiedlich zu sein, so dass es besser erschiene, zwei völlig getrennte Aufgaben daraus zu machen;
und die Schulbuchautoren scheinen ja auch bezweckt zu haben, dass sich a) und b) völlig unterschiedlich anhören;
mehr noch: im "realen" Leben liegen da ja auch tatsächlich zwei völlig unterschiedliche Probleme vor, die sich besser verdeutlichen lassen, wenn man mal annimmt, die "Geschichte" handle nicht von fünf Geschwistern, sondern von fünf KlassenkameradInnEn:
a) würde dann etwa bedeuten, dass man reihenweise ineinander verliebt ist und im abgedunkelten Kino zwecks Schmusen & Fummeln hübsch pärchenweise nebeneinander sitzen möchte (mit einem Mauerblümchen am Rand)
(hier hört die lebensweltliche Parallele allerdings schon auf, denn natürlich will da jeder Junge neben "seinem" und nicht - wie in Aufgabe a) - neben irgendeinem Mädchen sitzen;
und überhaupt probiert man im "realen" Leben ja nicht sämtliche Möglichkeiten aus),
b) könnte dann etwa bedeuten, dass ein Lehrer zwei ewige männliche Störenfriede im Klassenraum möglichst weit auseinander setzen möchte, wozu er drei weibliche Betablocker dazwischen setzt;
spätestens aber, wenn man auf Anhieb sieht oder dem Lösungsband entnimmt, dass in a) und b) dasselbe mathematische Ergebnis herauskommt, macht es natürlich größten Sinn, a) und b) als Teilaufgaben derselben Gesamtaufgabe (11) anzusehen.
Die übliche Vorgehensweise im Mathematikunterricht ist wohl, dass man die Teilaufgaben nacheinander ausrechnen lässt - und nach der zweiten vielleicht nichtmal merkt, dass da dasselbe wie in der (schon lange vergessenen) ersten herauskommt.
Mir hingegen scheint - und das haben die Schulbuchautoren auch wohl bezweckt -, dass man am Ende stutzen und sich überlegen sollte, warum in a) und b) dasselbe herauskommt
(überhaupt erst dann macht die Behandlung beider Aufgaben "Sinn"!).
Oder man rechnet erst gar nicht, sondern geht von den identischen Lösungen im Lösungsband aus und fragt davon ausgehend, weshalb sie identisch sind
(vgl. auch
"den Ergebnissen nachgehen (statt sie nur zu akzeptieren)").
Während man bei Algebra-Beispiel oben noch sagen könnte, dass SchülerInnen auch mal alle umständlichen Rechnungen durchgeführt haben sollten, um sie allesamt immer wieder zu üben und dadurch auch auf die Dauer (hoffentlich) besser zu beherrschen, reicht meiner Meinung nach beim kombinatorischen Beispiel der Beginn mit den fertigen Ergebnissen.
Denn dazu muss man herausfinden, wieso hinter den scheinbar unterschiedlichen Konstellationen in a) und b) letztlich dennoch dasselbe mathematische Problem steckt.
| Und genau das, also das Erkennen derselben mathematischen Struktur hinter (vordergründig bzw. aus mathematischer Sicht) unterschiedlichen Problemen, ist doch geradezu Mathematik. |
Schauen wir uns dazu die beiden Konstellationen a) und b) genauer an:
zu a): die einzig mögliche Kombination ist
M J M J M Und nun können nur noch die Mädchen untereinander bzw. die Jungen untereinander ihre Plätze tauschen.
Der einfachste "Fixpunkt" dabei ist, dass die beiden Jungen ihre festen Plätze haben:
J J Nun folgt:
es gibt 2 Möglichkeiten, die Jungen derart zu setzen,
es gibt 3! = 6 Möglichkeiten, die "restlichen" Mädchen zu verteilen,
insgesamt gibt es also 2 • 6 = 12 Möglichkeiten, Jungen und Mädchen zu verteilen.
zu b): die einzig mögliche Kombination ist
J M M M J Und nun können nur noch die Mädchen untereinander bzw. die Jungen untereinander ihre Plätze tauschen.
Der einfachste "Fixpunkt" dabei ist, dass die beiden Jungen ihre festen Plätze haben:
J J Nun folgt:
es gibt 2 Möglichkeiten, die Jungen derart zu setzen,
es gibt 3! = 6 Möglichkeiten, die "restlichen" Mädchen zu verteilen,
insgesamt gibt es also 2 • 6 = 12 Möglichkeiten, Jungen und Mädchen zu verteilen.
Und nun könnte man verallgemeinern und beispielsweise sagen, dass es natürlich auch für die Kombination
J M J M M
12 Möglichkeiten gibt.
Mit solchen vergleichenden Überlegungen würden die SchülerInnen aber besonders gut lernen, wie man überhaupt solche Probleme angeht: nicht mühsam alle erdenklichen Kombinationsmöglichkeiten aufzuzeichnen / zu zählen
(mit der Gefahr, welche zu übersehen oder mehrfach zu zählen),
sondern sich einfache "Fixpunkte" (die Verteilung der Jungen) zu suchen
(und der Rest [die Verteilung der Mädchen] läuft dann "wie geschmiert").