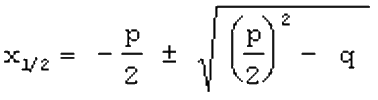
hübschhässliche quadratische Gleichungen

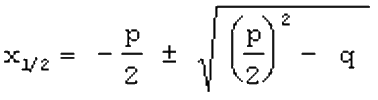
"Hübschhässlich habt ihr´s hier."
(Heinz Rühmann)

Vorüberlegungen
wie kommt man zur quadratischen Ergänzung?

Hier sei mal (wieder) davon abgesehen, wozu solch quadratische Gleichungen (außermathematisch) "gut" sein könnten.

Kein Zweifel kann aber bestehen, dass sie in der derzeitigen Schulmathematik eine enorme Rolle spielen.

Fragt sich nur, ob die Gewohnheit auch sinnvoll ist.

Mir scheint zumindest, dass die quadratischen Funktionen

(wie auch vieles anderes, wenn nicht gar fast alles in der [Schul-]Mathematik)

nur von innermathematischer Bedeutung sind

("nur"???):

• mit dem Exponenten 2 ergeben sich die ersten nichtlinearen Funktionen

(wenn man mal von den evtl. lange vorher arg kurz durchgenommenen, also längst vergessenen antiproportionalen Funktionen absieht),

• quadratische Gleichungen sind die ersten, an denen man fast alles kann

(weil es überhaupt erstmals bedeutsam wird): 

Symmetriebeweis, Nullstellen- sowie Scheitelpunkts-, also Minimaxberechnungen.

• und last but not least: die Funktionsgraphen zu quadratischen Gleichungen, nämlich Parabeln, sind einfach schön:

• 

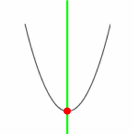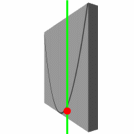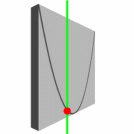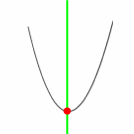
Anlass für meine Überlegungen hier ist die (rhetorische!) Frage eines Kollegen, ob SchülerInnen der 11. Klasse noch quadratische Gleichungen beherrschen müssten, wenn doch Computerprogramme

• diese automatisch berechnen

• und viel interessantere Möglichkeiten der Funktionsbetrachtung eröffnen würden.

Die Diskussion ist inzwischen auch nicht mehr gerade neu: inwieweit

• können Computer den SchülerInneN unsinnige Rechenarbeit abnehmen?

(Denn vor lauter  [angeblich unumgänglichem und leicht zu bewertendem] Rechnen kommen die SchülerInnen ja oftmals nie zur eigentlichen Mathematik.)

• können und müssen Computer den Mathematikunterricht (Methoden, aber vor allem Inhalte) verändern?

• bleiben aber auch gewisse Rechentechniken (Handwerkszeug!) unverzichtbar?

Schlimm ist da wohl nur jede Einseitigkeit.

Meine Reaktion auf den indirekten (gemeinten!) Vorschlag des Kollegen, in der 11. Klasse nicht noch mal halbwegs fundiert die quadratischen Funktionen (genauer: Berechnungen an ihnen) durchzunehmen, war kurz und knapp:

Dabei geht es mir gar nicht so sehr um die Beherrschung der Rechentechnik, also letztlich die Kenntnis und Anwendung der Formel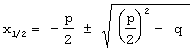

(die lässt sich - falls man sie vergessen hat - nachschlagen, und einschlägige Computerprogramme berechnen die Nullstellen intern mit dieser Formel, so dass man diese Formel überhaupt nicht mehr kennen muss),

sondern um etwas anderes:

1. die quadratischen Funktionen sozusagen als Startrampe in den eigentlichen Sinn der 11. Klasse, nämlich

• allgemeinere Funktionsbetrachtungen 

(vgl. ),

• und die Ableitung: bei den quadratischen Funktionen können wir noch etwas (s.o.: Minimaxberechnungen), was wir bei Funktionen höheren Grades nicht mehr können, wozu wir dort also neue Mittel brauchen. Ich sehe da eine gewisse (wenn auch rein innermathematische) "Forschungsmotivation".

(Das Problem lässt sich - nebenbei - durchaus schon näher eingrenzen:

• für die Minimaxberechnung suchen wir Punkte mit waagerechter Tangente,

• quadratische Funktionen sind nachweisbar achsensymmetrisch zu Parallelen zur y-Achse durch die bereits berechenbaren Scheitelpunkte; Funktionen dritten Grades scheinen punktsymmetrisch zu einer Art [noch nicht berechenbaren] Wendepunkt zu sein.)

2. Interessanter als die Formel 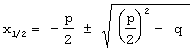 ist doch ihre Herleitung

(die man auch kennen sollte, falls

1. man die Formel vergessen hat,

2. man sie falsch in Erinnerung hat,

3. mal wieder alle Computer ausgefallen sind,

4. man die Formelsammlung zu Hause vergessen hat).

Mir scheint sogar, dass man (exemplarisch) anhand der Herleitung dieser Formel etwas enorm Wichtiges für die gesamte Mathematik lernen kann - und dass diese Herleitung daher auch schon (wie üblich) in der 9. Klasse mit der gehörigen Dramatik erfolgen sollte.

3. Sollte - erst durch die erlebte Herleitung? - ihre "Bedeutung" in doppeltem Sinne verstanden werden:

• zwar ist die Formel "ganz schön kompliziert", aber eben auch enorm praktisch, macht nämlich viele mühsame Rechnungen überflüssig,

• sollte jedes Einzelbestandteil der Formel verstanden (veranschaulicht) werden.

Kleines Intermezzo:

Das Problem sei anhand einer noch relativ einfachen quadratischen Funktion erörtert, nämlich anhand von

f: y = x² - 6x + 8 .

Gesucht seien die Nullstellen dieser Funktion, was auf die Frage hinaus läuft, wann gilt:

0 = x² - 6x + 8 ?

(Nebenbei: man könnte sich fragen, ob es nicht sinnvoller ist, mit den bereits bekannten Nullstellen anzufangen, also - das sei schon verraten - im vorliegenden Fall mit x = 2 und x = 4.

Daraus ergäbe sich

        x      = 2 oder x       = 4

   x - 2 = 0 oder x - 4 = 0

(x - 2)      •      (x- 4) = 0

 x² - 6x + 8               = 0 ,

womit sich dann die Frage stellen würde, ob und wie man umgekehrt aus x² - 6x + 8 wieder die Nullstellen rausdestillieren könnte.)

Auf die Frage, wann (für welche x) denn 0 = x² - 6x + 8 gilt, wird vermutlich üblicherweise geantwortet:

"Da macht man eine quadratische Ergänzung

(über deren Funktionieren man sich schon gar nicht mehr wundert),

und da die SchülerInnen darauf sowieso nicht von selbst kommen werden, mache ich das vor - und »dürfen« sie es dann hinterher zigtausendfach auf andere quadratische Funktionen »anwenden« (Schema F)."

Nun geht es mir hier nicht darum, ob SchülerInnen die quadratische Ergänzung (und andere mathematische Sachverhalte) wirklich selbst entdecken können

(ich vermute mal, das können sie - und könnten auch wir LehrerInnen - nicht).

Aber es gibt ein "angeleitetes Selbstentdecken" bzw. einen "halbkreativen" Nachvollzug der Mathematikgeschichte (vgl. ) - und genau das sollte erheblich mehr im Mathematikunterricht gemacht werden (gerne auf Kosten anderer Stoffe).

Dieses "angeleitete Selbstentdecken" besteht (wie ich unten zu zeigen versuchen werde) im vorliegenden Fall (und auch sonst oftmals) gerade darin,

• sich die umfassenden Schwierigkeiten, die auf dem Weg zur Lösung lauern, klar zu machen

(Schwierigkeiten, die viele MathematikerInnen vor lauter Standardverfahren längst nicht mehr sehen und  die sowieso ausgeschaltet werden, wenn man den Lösungsweg einfach nur vormacht),

• daraus aber auch typische (über das Einzelproblem hinausgehende) Lösungsstrategien zu entwickeln.

Aus der oben zitierten Kollegenfrage(?),

ob SchülerInnen der 11. Klasse noch quadratische Gleichungen beherrschen müssten, wenn doch Computerprogramme diese automatisch berechnen [...],

höre ich einen resignativen Unterton heraus:

"Selbst wenn man in der 11. Klasse die quadratischen Gleichungen ausführlich durchnimmt (wiederholt), lernen »die« SchülerInnen es ja doch nicht."

(Ist der Computer da eher Ausflucht und Anbiederung als Ergänzung?

Denn merke: zwar wird der Computer oftmals pauschal eingesetzt, aber kaum jemals überlegt, was [genauer: was an Mathematik] man damit besser lernen kann.

Und resignativ ist es oftmals noch in anderer Hinsicht: warum beispielsweise noch die Bruchrechnung "beibringen", wenn die SchülerInnen sowieso alles mit Taschenrechner rechnen und ihnen dieser realistischerweise - selbst wenn man es wollte - gar nicht mehr zu verbieten ist?)

Warum - wenn´s denn stimmt - lernen "die" SchülerInnen "es" denn nicht, d.h.

• können sie schon bald (wenn überhaupt jemals) quadratische Gleichungen nicht mehr lösen

• und wissen sie nicht mehr, wie korrekt mit umzugehen ist

(wenn sie diese Formel überhaupt noch kennen bzw. wissen, dass sie bei quadratischen Gleichungen hilft)?

Mir scheint, es liegt daran, dass sie eben nur das "Schema F"

(die ja auch nicht gerade einfache Formel )

kennen gelernt haben, die im besten Fall einmal kurz vorgemacht wurde, so dass die Herleitung und der Hintersinn nicht durchschaut wurden.

(Seien wir ehrlich: oftmals macht man als LehrerIn Herleitungen und Beweise nur der "mathematischen Korrektheit" wegen - und denkt insgeheim [sagt es sogar laut?]: "letztlich müsst ihr nur das »Schema F« kennen." Und dementsprechend sehen dann auch die reinen Einsetz- bzw. Rechenklausuren aus.)

Wie so oft in der (Schul-)Mathematik ist eine scheinbar einfache Sache (hier die Berechnung der Nullstellen) eben nur dann einfach, wenn man den "Trick" schon kennt

(ihn - und das geht vor allen LehrerInneN so - allzu gewohnt ist).

In Wirklichkeit aber stecken dahinter (zumindest für SchülerInnen) ganz enorme Schwierigkeiten, bzw. die Herleitung bedarf schon einer Fülle von Überlegungen und stabiler sowie jederzeit präsenter Vorkenntnisse.

Schauen wir uns daher mal exemplarisch an, was alles zur Berechnung der Nullstellen nötig ist:

1. Ziel einer Lösung der Gleichung 0 = x² - 6x + 8 ist wie immer eine Umformung in

x = ? ,

d.h. wir wollen wissen, was EIN x (ohne "Quadrat oben dran") ist

(vgl. ).

2. Wegen des Quadrats schreit 0 = x² - 6x + 8 danach, es mittels Wurzelziehen ungeschehen zu machen.

Und prompt lauert eine typische Fallgrube:

• 1. Fehlerart:
  weil nur x² quadratisch ist, zieht man nur daraus die Wurzel, rechnet also

         x² - 6x + 8 = 0 |  

(d.h. Wurzelziehen aus beiden ganzen Seiten der Gleichung)

        

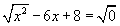
   x  - 6x + 8  =   0

      -5x   +  8 =   0

Und prompt hat man die ursprünglich quadratische Gleichung unbemerkt und falsch zu einer linearen vereinfacht.

(Der Fehler lag natürlich - und zwar bei  - darin, dass man eben nicht, wie vorgeschrieben, aus der ganzen linken Seite die Wurzel gezogen hat.
Und die Äquivalenzzeichen sind natürlich falsch bzw. unzulässig. Ich hatte sie nur gesetzt, weil sie so häufig unverstanden benutzt werden ["der Lehrer will die halt haben"] und man gar nicht bemerkt, wie die Äquivalenz schleichend abhanden kommt.)

• 2. Fehlerart: