der Treppenwitz des Rechenschiebers
(sowie ein bisschen über Logarithmen)

Der Rechenschieber verhält sich zum Computer (Taschenrechner) wie eine Dampflok zum ICE:

• natürlich ist ein Computer/ein ICE "schnittig" und rasend schnell, aber der Laie hat kaum eine Chance, sie (ihre Funktionsweise) zu verstehen

(in der Tat ist unsere gesamte Alltagstechnik randvoll mit Mathematik und Physik, aber das funktioniert nur, weil der Anwender die mathematisch-naturwissenschaftlichen Hintergründe nicht kennen und benutzen muss);

• im Vergleich damit sind Rechenschieber und Dampfloks Schnecken, aber man kann ihnen immerhin noch ansehen, wie sie funktionieren:

Im Unterricht habe ich festgestellt, dass heutige SchülerInnen, obwohl doch Kinder des Hightech-Zeitalters, durchaus noch an mechanischen Rechengeräten

(und der Herkunft der "fertigen" Ergebnisse des Taschenrechners; vgl. )

interessiert und von der Faszination des "BeGREIFbaren" fasziniert sind:

1. am Beispiel des Rechenschiebers,
2. am Beispiel der in meinem Besitz befindlichen mechanischen Rechenmaschine "Brunsviga 15e" (1935-1947):

An dieser Rechenmaschine ist schon allein faszinierend, dass sie bei relativ kleinen Ausmaßen (ca. 20 cm • 20 cm • 20 cm) satte 12 kg wiegt, weil sie fast vollständig aus Stahl ist:

Das Rechnen mit dieser Maschine

(mittels der Zahlenräder und der vielen Hebel links und rechts)

ist selbst bei "einfacheren" Rechnungen äußerst umständlich

(vgl. ; gezippte Bedienungsanleitung),

aber vielleicht macht gerade dies überhaupt erst dankbar für elektronische Rechner.

Wenn man die Maschine öffnet, sieht man eine ganze Batterie von "Rechenwalzen", was doch Respekt für die Ingeniosität der Maschine erzeugt.

Aber man kann kaum verstehen, wie nun all die Zahlenräder, Hebel und Rechenwalzen zum Ergebnis führen.

Zum Verständnis viel geeigneter ist also allemal der Rechenschieber.

Wie so oft

(vgl. etwa )

gilt: "reduce to the max(imum)" bzw. , d.h. man specke "den" Rechenschieber ab bzw. nehme einen möglichst einfachen:

• also nicht einen mit massenhaften Rechenmöglichkeiten wie z.B.

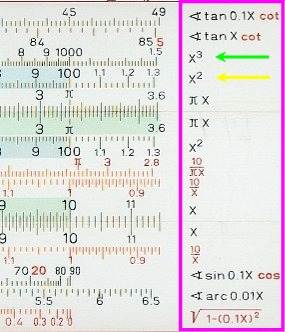
(hier ist nur der rechte Rand abgebildet, an dem deutlich wird, dass man bei diesem Rechenschieber mit speziellen Logarithmengesetzen [s.u.] beispielsweise auch sehr einfach x³ und x ² berechnen kann;
und es gibt noch massenhaft Rechenschieber für Spezialfälle),

• sondern einen, der nur die Grundfunktionen beherrscht:

"Logarithmus (mathematische Größe): Der seit dem 17. Jh. bezeugte mathematische Fachausdruck ist eine Prägung des schottischen Mathematikers John Napier (1550-1617) aus griech. lógos »Wort; Rechnung; Verhältnis« und griech. arithm»s »Zahl«." (Duden Herkunfts-Lexikon) Logarithmen setzen also zwei Zahlen (im Folgenden 8 und 2)  in ein Verhältnis, und zwar nicht, wie sonst üblich, mittels Division (z.B.: das Verhältnis von 8 zu 4 ist 8 durch 2 = 4, d.h. 8 ist viermal so groß wie 2), sondern über den Exponenten: (z.B. 2x = 8 x = 3  ; man schreibt auch logarithmus 2 8 = 3 ). Aber hier wie auch im Folgenden soll nicht ausführlich der Logarithmus erklärt werden.

Da die geniale Einfachheit des Rechenschiebers nun mal auf den Logarithmen beruht, sei ein kleiner Exkurs eben zu diesen Logarithmen eingeschoben.

Nun sind Logarithmen (schon allein dieser Name!) zweifelsohne das Angstthema vieler 10-KlässlerInnen - und vielleicht kann man gerade mittels des Rechenschiebers doch wieder einen Weg zu ihnen finden.

Es gibt bzw. gab vier gute Gründe für die Verwendung von Logarithmen:

1. kann man mit Logarithmen sehr gut einen überblick über sehr große Zahlen gewinnen

_{(weil der Logarithmus einer Zahl viel kleiner als diese Zahl selbst ist; s.u.)}.

2. gibt es natürliche Prozesse, die tatsächlich logarithmisch verlaufen

(vgl. etwa

"die wahrgenommene Lautstärke ist nun einmal ein logarithmisches Maß (dummerweise nicht zum Zehnerlogarithmus wie das dB [= Dezibel] sondern zum Zweierlogarithmus, aber das ist eine andere Geschichte)."
(Quelle: )

Oder anders gesagt: wenn die Lautstärke objektiv doppelt so hoch ist, wird sie als viermal so hoch wahrgenommen.)

3. sind Logarithmen nunmal unabdingbar, um Exponentialgleichungen lösen zu können

(wozu das Logarithmengesetz log (a^x) = x  • log (a) dient, mittels dessen der Exponent "davor gezogen" werden kann und somit aus einer [schwierigeren] Potenz eine [einfachere] Multiplikation wird;

hier sei nicht diskutiert, weshalb man Exponentialgleichungen lösen können sollte, sondern einfach vorausgesetzt, dass das im Matheunterricht nach wie vor nötig ist).

4. erleichtern Logarithmen erheblich das Rechnen, indem sie u.a.

• wegen des Logarithmengesetzes log (a ●  b) = log a + log b die schwierigere Multiplikation auf eine einfachere Addition reduzieren

(ganz verwunderlich ist das ja nicht, da die Multiplikation sowieso eine verkürzte Addition ist; vgl. etwa 3 ●  4 = 3 + 3 + 3 + 3);

• wegen des Logarithmengesetzes log (a :  b) = log a - log b die schwierigere Division auf die einfachere Subtraktion reduzieren.

Die Logarithmen sind also ein schönes Beispiel für : da wurde mit den Logarithmen ein hochkompliziertes Instrumentarium erdacht, mit dem dann, wenn es erstmal vorhanden ist, das alltägliche Rechnen erheblich einfacher ist.

Generationen von MathematikerInnen haben also mühsamst sogenannte Logarithmentafeln erstellt, d.h. jeden Einzelwert

(noch ohne Computer, sondern "mit der Hand"!)

berechnet:

Und mittels solch fertiger, oft hunderte von Seiten langer Logarithmentafeln wurde dann das Rechnen für "Normalsterbliche" erheblich einfacher.

(Ich hab's in meiner Schulzeit noch erlebt: die Logarithmentafel war - mangels Taschenrechner - unser täglicher Begleiter.

Nebenbei: die Erstellung solcher Logarithmentafeln [und zwar noch ohne Computerhilfe] muss eine wahre "Idiotentätigkeit" gewesen sein, vor der man aber doch allemal Respekt haben kann. Und die Leute [!], die so sagenhaft gut rechnen konnten, nannte man damals "Computer"

... während der heutige [elektronische] Computer alle menschlichen Rechenfertigkeiten überflüssig [?] macht und verkümmern lässt).

Nun ist all das mit der Entwicklung des (elektronischen) Computers natürlich Schnee von gestern:

• keiner braucht zwecks Vereinfachung von Rechnungen noch Logarithmentafeln, sondern jeder vereinfacht sich die Rechnung mittels Taschenrechner/Computer;
• und im selben Augenblick erübrigt sich natürlich auch die Erstellung von Logarithmentafeln "per Hand".

Hier in 4. ist also zur Vergangenheitsform überzugehen:

• "[...] erleichterTEn Logarithmen erheblich das Rechnen",
• "da wurde mit den Logarithmen ein hochkompliziertes Instrumentarium erdacht, mit dem dann, wenn es erstmal vorhanden ist, das alltägliche Rechnen erheblich einfacher WAR."

Es gibt also keine aktuelle Notwendigkeit mehr, im Schulunterricht noch die Logarithmengesetze

• log (a ●  b) = log a + log b
• log (a :  b) = log a - log b

durchzunehmen, sondern es reicht, laut 3. das Logarithmengesetz

• log (a^x) = x  • log (a)

zu behandeln.

Der Schulunterricht wird sich also ändern müssen, indem

• 1.-3. deutlicher betont werden

(und zwar auf Kosten von 4.?),

• und/oder indem ein neuer Zugang zu 4. versucht wird, und zwar
  • nicht mehr, weil man die dort genannten Logarithmengesetze wirklich braucht,
  • sondern weil man an ihnen vielleicht besonders gut verstehen kann, was Logarithmen überhaupt sind und wie sie funktionieren.

   

  Und da eben scheint mir der "historische" Zugang über Rechenschieber durchaus geeignet, und zwar nicht etwa, weil die SchülerInnen noch bzw. wieder mit Rechenschiebern rechnen sollten, sondern weil der Rechenschieber als mechanisches Instrument so "beGREIFbar" ist.

Zu Beginn des Exkurses über Logarithmen war oben schon erwähnt worden, was jetzt wohl endlich genauer zu erklären ist: dass nämlich

"[...] die geniale Einfachheit des Rechenschiebers nun mal auf den Logarithmen beruht."

Schauen wir uns dazu nochmals den besonders einfachen Rechenschieber

an, reduzieren ihn aber noch weiter auf den zentral wichtigen Ausschnitt

,

also

Hier sei auch schon erwähnt, weshalb der Rechenschieber überhaupt "-Schieber" heißt: während die obere und die untere Leiste fest (auf der Unterseite des Rechenschiebers verbunden) sind, lässt sich zwischen diesen beiden die mittlere verschieben:

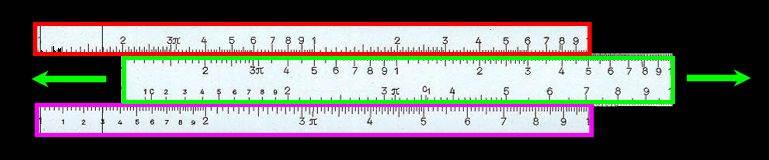
Aber zu dieser Verschiebung kommen wir dann später
nochmal. Vorerst interessiert uns nur eine einzige (Teil-)Skala des Rechenschiebers, nämlich

,

also (indem wir noch einen störenden Strich und das hier uninteressante löschen)

.

An dieser Skala sollen uns nun aber der Einfachheit halber nur die ganzen Zahlen 1, 2, 3, 4, 5, 6, 7, 8 und 9 interessieren.

Und da könnte einem doch auffallen, dass sie nicht

(wie etwa auf einem Lineal)

in gleichem Abstand liegen, sondern nach rechts hin immer näher beieinander.

Warum?

Eben weil sie logarithmisch angeordnet sind - und das funktioniert so

(wobei ich hier weglasse, wie der jeweilige Logarithmus berechnet wird):

man nehme von jeder  ganzen Zahl den Logarithmus, also

Zahl	Logarithmus
1	log (1) = 0
2	log (2) ≈ 0,30
3	log (3) ≈ 0,47
4	log (4) ≈ 0,60
5	log (5) ≈ 0,69
6	log (6) ≈ 0,77
7	log (7) ≈ 0,84
8	log (8) ≈ 0,90
9	log (9) ≈ 0,95

Und nun tragen wir die Logarithmen auf einem Zahlenstrahl ein

(zur Erinnerung aber auch oben drüber, von welcher ursprünglichen Zahl die Logarithmen herstammen):

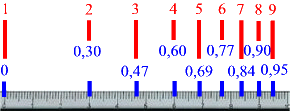
Und jetzt kommt

eigentlich muss man

1. zuerst zu jeder behandelten Zahl den Logarithmus finden,
2. dann mit den Logarithmen rechnen (s.u.)
3. und zuguterletzt das Ergebnis aus 2. wieder in "normale Zahlen" ("Numerus") rückübersetzen.

Nun markiert man aber den Zahlenstrahl nicht mit den Logarithmen, sondern mit den ursprünglichen Zahlen, so dass sich ergibt:

Und damit eben haben wir exakt die o.g. Skala

!

Es gilt also:

Und damit zum

der allerdings letztlich "nur" auf dem bereits oben genannten unscheinbaren Logarithmengesetz

log (a ●  b) = log a + log b

beruht.

Es sei nochmals daran erinnert, dass mit diesem Logarithmengesetz die schwierigere  Multiplikation auf eine einfachere Addition reduziert wird.

Und eben solche Additionen lassen sich

(im Gegensatz zu Multiplikationen!)

auch mechanisch durchführen, indem man höchst einfach Skalen/Zahlen hintereinander legt.

Schauen wir uns dazu den Rechenschieber nochmals genau an: die soeben hergeleitete Skala

taucht auf dem Rechenschieber nämlich zweimal auf:

Und hier kommt nun - zwecks "Hintereinander-Legen" - die Eigenschaft des Rechenschiebers zum Tragen, dass die mittlere Schiene verschiebbar ist:

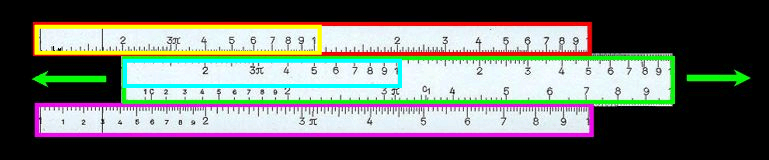
Genau genommen wird also nicht hintereinander gelegt, sondern parallel zueinander verschoben/angeordnet.

Wirklich hilfreich ist der Rechenschieber natürlich nur, wenn kompliziertere Zahlen (z.B. mit Nachkommastellen) miteinander multipliziert werden sollen, man also die Rechnung nicht so leicht "im Kopf" durchführen kann.

Dennoch lässt sich das Prinzip

(nach dem dann auch kompliziertere Zahlen miteinander multipliziert werden)

am besten an sehr einfachen Zahlen zeigen, also z.B. der Multiplikation von 2 und 4:

1. schiebt man den  Anfang/Nullpunkt der hellblauen Skala unter die 2 in der gelben Skala,
2. geht man nun auf der hellblauen Skala zur 4 und
3. liest man dann darüber in der gelben Skala das Ergebnis 8 ab:

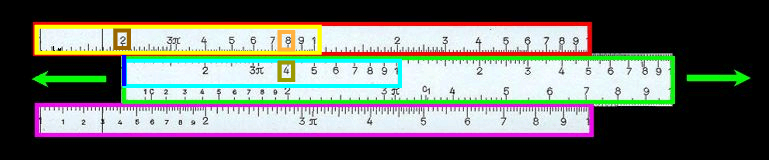
Kurz eingeschoben sei, dass geübte Rechenschieberbenutzer

(wie auch japanische Abakus-Benutzer)

enorm schnell waren, ja teilweise

(u.a., da es "nur" um überschlagsrechnungen geht; s.u.)

sogar schneller als etwa Taschenrechnerbenutzer.

Die Nachteile des Rechenschiebers sind auch fast seine Vorteile:

1. ermöglicht er wegen der geringen Ablese- und Einstellgenauigkeit nur ungenaues Rechnen,
2. ist die Position des Kommas im Ergebnis unklar,
3. sorgt all das aber dafür, dass

• der Benutzer immer mitdenken muss, also nicht Ergebnisse unkontrolliert glaubt wie oftmals beim Computer,
• vor allem überschlagsrechnungen möglich sind, also ein Gespür für die Größenordnungen trainiert wird.

"Treppenwitz der Weltgeschichte Mit diesem Ausdruck kennzeichnet man eine ziemlich absurd, wie ein schlechter Scherz wirkende Begebenheit, die zu einem sie begleitenden historisch bedeutsamen Vorgang in keinem angemessenen Verhältnis steht, ihn aber gelegentlich in nicht unerheblichem Maß beeinflusst. [...]" (Duden  Herkunfslexikon)

Der Treppenwitz des Rechenschiebers ist aber, dass er

• zwar Zahlen miteinander multiplizieren kann

(indem er ihre Logarithmen addiert),

• aber nicht die Zahlen selbst addieren kann.

Er beherrscht also wohl das Schwierige, nicht aber das Einfache, weshalb man auch sagen könnte, dass er vor lauter Kraft kaum gehen kann.