Vgl. auch 

"dis|kret [lat.-mlat.-fr.]: 1. a) so unauffällig behandelt, ausgeführt o.ä., daß es von anderen kaum od. gar nicht bemerkt wird; vertraulich; b) taktvoll, rücksichtsvoll; Ggs. indiskret. 2. a) (von sprachlichen Einheiten) abgegrenzt, abgetrennt, abgrenzbar, z. B. durch Substitution (Sprachw.); b) in einzelne Punkte zerfallend, vereinzelt, abzählbar (bezogen auf eine Folge von Ereignissen od. Symbolen; Techn.); -e Zahlenwerte: Zahlenwerte, die durch endliche Intervalle voneinander getrennt stehen (Math., Phys.)."
(Duden Fremdwörter)

Das Problem der "(Un-)Stetigkeit" taucht allerdings auch in ganz anderen Zusammenhängen auf, nämlich z.B. bei der Herleitung von

(vgl. ).

Der klassische Beweis, dass die Wurzel aus 2 irrational ist, ist einerseits in seiner Raffiniertheit "schön", andererseits aber auch für SchülerInnen eine echte Zumutung, und zwar

1. eben wegen der Raffiniertheit, nämlich der indirekten Vorgehensweise,
2. , weil das irrationale Ergebnis schlichtweg unvorstellbar ist.

Und das liegt sogar

• weniger daran, dass die Ziffern hinterm Komma völlig unregelmäßig (nicht periodisch) folgen,
• sondern daran, dass (wie durchaus auch bei periodischen Zahlen) unendlich viele Ziffern auftreten.

Und doch erleben SchülerInnen das bei periodischen Zahlen, also z.B. = 0,333333333333..., nicht so sehr als Problem, und zwar wohl ganz einfach deshalb, weil es da im Unterricht nicht so sehr vom Lehrer (über-?)problematisiert wird.

Schauen wir uns mal das klassische Beispiel zur Herleitung der Wurzel aus 2 an:

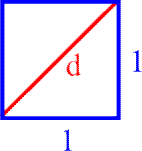
Gegeben sei die einfachste überhaupt denkbare Fläche, nämlich ein Quadrat mit der Seitenlänge 1. Auf einigen Umwegen wird dann gezeigt:

1. dass die wiederum einfachste denkbare Strecke im Quadrat, nämlich die Diagonale d, die Länge hat,
2. dass diese irrational ist.

Wie bereits gesagt, interessiert uns an dieser Irrationalität vorerst nur, dass (wie bei periodischen Zahlen) nach dem Komma noch unendlich viele Stellen folgen.

Hier nur der Anfang: 1,4142135623730950488016887242097

Heißt "unendlich viele Stellen" nicht aber, dass die Diagonale immer länger und länger wird?

(Da hilft es SchülerInnen wenig, dass diese Zahl z.B. nie größer als z.B. 1,5 wird, sondern sie verfallen erstmals in Schockstarre über den Limes[-prozess].)

Wie aber kann die Diagonale immer länger werden, wenn die Quadratseiten, durch die die Diagonale "eingesperrt" ist, sich nicht verändern, sondern immer die Länge 1 behalten?

Nun gibt es verschieden Möglichkeiten, auf das Problem zu reagieren:

1. ist es einem (wie alle Mathematik) herzhaft egal und damit auch wenig stauenswert,
2. will man "es" so genau (auf die zigste und hundertste Nachkommastelle) gar nicht wissen,
3. staunen die SchülerInnen weniger als der Lehrer, überproblematisiert er also aus ihrer Sicht,
4. wenden kluge SchülerInnen vielleicht berechtigt ein, dass irgendwann der atomare Maßstab erreicht sei (sozusagen das letzte Atom auf der Diagonalen) und danach weitere Nachkommastellen gar nicht möglich seien

(genauso gut könnte man einwenden, dass schon das Quadrat mit der exakten Seitenlänge 1 nicht nur aus technischen Gründen, sondern auch prinzipiell [wegen des letzten Atoms] nicht möglich sei).

Hier bei d. kommt aber oft ein typischer Schuleffekt zum Tragen: eine Schulmathematik, die sich an einem steif linearen Curriculum statt immer mal wieder und langfristig an zentralen mathematischen Überlegungen orientiert, drängt oftmals die durchaus im Hinblick auf diese zentrale mathematische Überlegungen ergiebigen "Kinderfragen" von Laien (SchülerInnen) beiseite, ja, denunziert sie geradezu als dumm, statt sie mathematisch "ernst" zu nehmen und zu nutzen.

Wenn ich's halbwegs richtig verstanden habe, ist die Natur nämlich auf dem allerkleinsten Maßstab "krümelig", d.h. es ist keine feinere Einteilung möglich als die der Elementarteilchen

(seien es die Atome, die Elektronen/Neutronen/Protonen, die Quarks oder Strings).

Oder anders gesagt: es gibt kleinste (!) Teile, die somit

(soweit wir bislang wissen)

nicht mehr weiter unterteilbar sind. D.h. die Natur ist auf diesem kleinsten Maßstab nicht sämig bzw. kontinuierlich oder stetig, sondern krümelig bzw. diskret

(und soweit wir wissen, liegen die Elementarteilchen keineswegs eng gepackt nebeneinander, sondern gibt es zwischen ihnen "riesige" leere Räume:   ).

Wenn nun aber die Mathematik trotz der Elementarteilchengrenze weiter misst bzw. einteilt, so

(und das zu vermitteln, ist ungeheuer schwierig)

betreibt sie keinen Blödsinn, sondern

(so recht nach dem Motto "wir pfeifen auf die einschnürenden Grenzen der schnöden [physikalischen] Wirklichkeit")

lustvolle "Meta-Physik":

Interviewer: „Wie würden Sie reagieren, wenn die allgemeine Relativitätstheorie nicht empirisch bestätigt worden wäre?“ Einstein: "Da könnt mir halt der liebe Gott leid tun. Die Theorie stimmt doch."

Die Einteilung der Natur in allerkleinste, nicht mehr weiter unterteilbare Einheiten hat nun aber den Physikern allergrößte Probleme bereitet und seit Max Planck (der Hohlraumstrahlung) und dann Einstein dazu geführt, auch bei Energien kleinste Einheiten, nämlich diskret-nichtstetige sogenannte "Quanten" anzunehmen.

Oder die Physiker geraten in erhebliche mathematische (!) Schwulitäten, wenn es im ganz Großen (bei schwarzen Löchern) doch wieder zu unendlich kleinen Effekten ("Singularitäten") kommt, da dann die größte aller denkbaren mathematischen Katastrophen, nämich eine Division durch Null stattfindet.

Aber verlassen wir vorerst die schnöde Physik und bleiben wir bei der Mathematik: eine nichtstetige Funktion ist beispielsweise auch der Tangens, also f: y = tan (x). Da entstehen "nicht behebbare Polstellen"

(u.a., weil auch hier sonst durch Null geteilt würde):

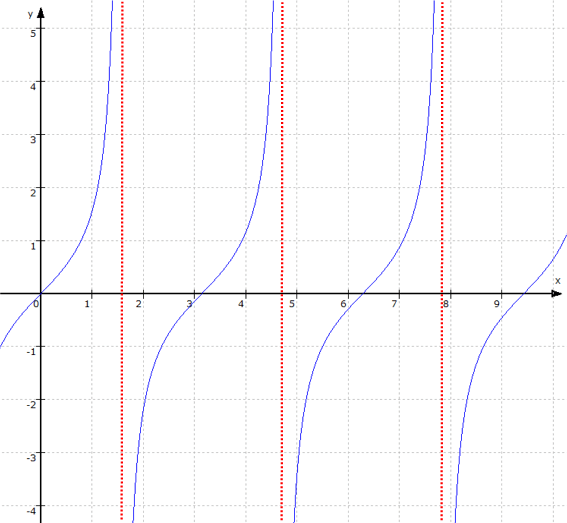
Und diese Funktion ist nicht stetig, weil sie nicht in einem "Wusch" zeichenbar ist, sondern man für jeden Zweig neu ansetzen muss.

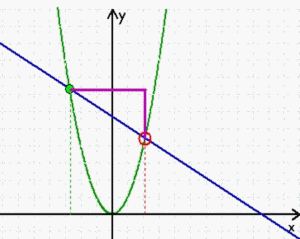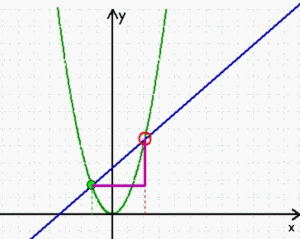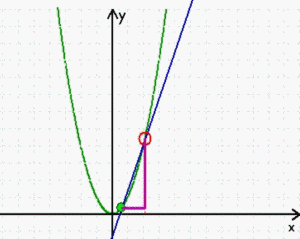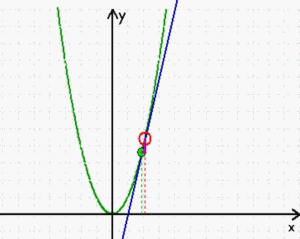
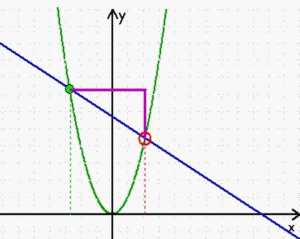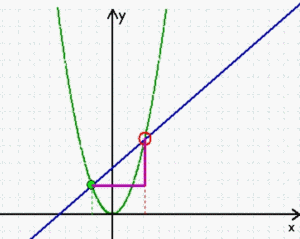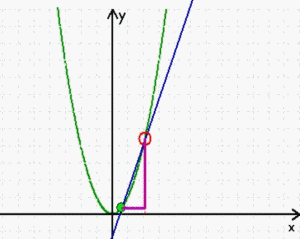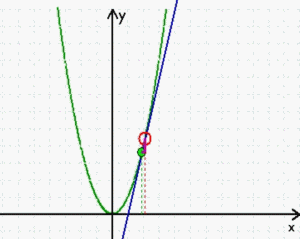
Wie schon gesagt, sind stetige Funktionen erheblich einfacher zu behandeln als nicht-stetige, aber es ist doch eine schöne Ironie, dass beispielsweise die "Ableitung" stetiger Funktionen dennoch "quasi-nicht-stetig" hergeleitet wird: da sich die Steigung in einem einzigen Punkt P nicht bestimmen lässt, zieht man eine Sekante durch P und einen weiteren Punkt Q und nähert dann diesen zweiten Punkt Q immer mehr dem ersten Punkt P an. In "Wirklichkeit" erfolgt diese Annäherung zwar durchaus stetig

(man "denkt" sich sämtliche, also unendlich viele Zwischenzustände),

aber

1. etwa an der Tafel zeichnet man nur einige wenige, nicht-stetig aufeinander folgende Zwischenzustände,
2. auch jedes Computerprogramm berechnet und zeichnet nur diskrete Zwischenzustände, die allerdings so schnell aufeinander folgen, dass sich für unsere "trägen" Augen dennoch ein stetiger "Film" ergibt:

→

Fernsehen und Kino sind also Musterbeispiele für Nicht-Stetigkeit: